Blog
The post is contributed by Mr. Kohei Shinohara, who joined PFN summer internship 2021.
Japanese version is available here.
Introduction
I’m Kohei Shinohara from Kyoto University, who participated in the PFN summer internship 2021 program. This article describes my work on the topic “Neural network potential with charge transfer”.
The implementation is available here.
In addition, slides are uploaded here.
Background
In the field of materials science, calculations based on density functional theory (DFT) are widely used to simulate materials on an atomic scale. It is known to be able to predict many material systems with high accuracy by solving the Schrödinger equation (with some approximation). On the other hand, DFT calculations are expensive in terms of computation time, which is a challenge for large-scale or long-time simulations.
To solve this problem, a method called neural network potential (NNP) [1] has been actively studied in recent years. Large number of DFT calculations are performed and used as a dataset so that neural network (NN) can predict its output. It is attracting attention as a method that has the potential to achieve both DFT-level accuracy and fast prediction. NNP is also a core technology in Matlantis, a universal atomic-level simulator launched in 2021 by Preferred Computational Chemistry, a joint venture established by PFN and ENEOS.
One important challenge of NNP is that there are some systems that are difficult to predict with conventional NNP. NNP usually reduces calculation time by considering only the contributions from neighboring atoms for each atom. However, this approach poses a problem for systems in which long-range interactions cannot be neglected. Examples of systems where it is important to consider long-range interactions include catalysts on material surfaces and ionic crystals. These long-range interactions physically originate from charge transfers [6] between atoms. Therefore, in the past few years, NNPs that take charge transfer into account have also been studied [2-5].
The Fourth-Generation Behler-Parrinello Neural Network Potential (4G-HDNNP, we denote it as 4G-BPNN in this blog) [4] is one of the most representative of these NNPs that take charge transfer into account. This paper reports that combining NNs with a classical method for charge transfer called Qeq (see below) improves prediction accuracy. On the other hand, 4G-BPNN is based on a multilayer perceptron (MLP) model, and it is not clear to what extent the proposed method is effective in Graph Neural Networks (GNN), which are becoming mainstream in NNP in recent years. In this internship, we implemented the method proposed in 4G-BPNN on a GNN basis and verified its effectiveness.
Method
Next, we will describe the GNN on which the implementation is based on, the electrostatic interaction term which captures long-range interactions, and a charge prediction technique called charge equilibration. For more detail, please refer to slides and references.
GNN Based NNP
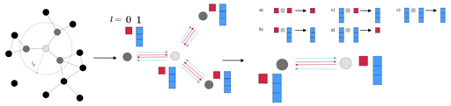
Figure 1: NequIP overview (taken from [7])
We used Neural Equivariant Interatomic Potentials (NequIP) [7], where its pytorch implementation can be found in [8], as the baseline model for NNP (Figure 1). NequIP is a GNN-based model in which the convolution layer updates each atom’s descriptor based on its neighbors. In addition, while NNP requires the output to be invariant when translational and rotational operations are applied to the input structure, NequIP guarantees invariance in the model itself. Such a model is called an SE(3)-equivariant network [9, 10].
Electrostatic interaction term
To calculate the energy of the long-range interaction, we predicted the charge from the descriptor of each atom obtained from the GNN and calculated the electrostatic interaction (equation below) from that charge [4].
$$
E_{\mathrm{ele}}(\{Q_{i}\}) = \frac{1}{2} \frac{1}{4\pi \epsilon_{0}} \int \int \frac{\rho(\mathbf{r}) \rho(\mathbf{r}’)}{|\mathbf{r} – \mathbf{r}’|} d\mathbf{r} d\mathbf{r}’
$$
We considered two methods for predicting the charge: one is to predict the charge directly from the descriptor of each atom, and the other is to predict it using Qeq, which will be presented in the next section.
Also, when the input structure is a periodic system such as a crystal, a special method called Ewald summation [11-13] is used to calculate the electrostatic interaction term. Since we could not find a pytorch implementation of Ewald summation, we implemented it by ourselves.
Charge Equilibration
4G-BPNN [4] and its prior work CENT [2] use a classical method called Charge Equilibration (Qeq) [14, 15] to predict charges. Qeq models the contribution to the charge-derived energy as
\[
E_{\mathrm{Qeq}}(\{ Q_{j} \}) = E_{\mathrm{ele}}(\{ Q_{j} \}) + \sum_{i} \left( \chi_{i} Q_{i} + \frac{1}{2} J_{i} Q_{i}^{2} \right)
\]
and determine charge \(Q_{i}\) by minimizing the energy \(E_{\mathrm{Qeq}}\).
When Qeq is combined with NN, NN predicts the parameters \(\chi_{i}\) and \(J_{i}\) which is necessary to calculate \(E_{\mathrm{Qeq}}\).
From the implementation’s point of view, solving Qeq corresponds to finding a solution of linear equations. In the pytorch implementation, this is achieved by using torch.linalg. solve. The complicated implementation of differentiation of the solution of linear equations can be avoided and by taking advantage of pytorch’s automatic differentiation.
Results and Discussion
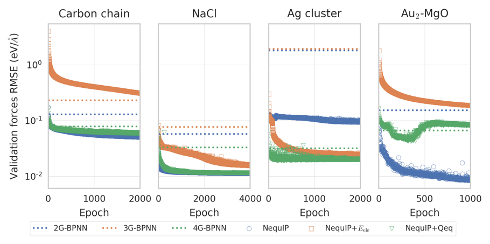
Figure 2: Comparison of prediction root-mean-square error (RMSE) of forces acting on each atom
We trained various types of NNP on the dataset used in the 4G-BPNN paper (please refer to p9 of slides for the dataset overview). Figure 2 plots the error of the force predictions acting on each atom. The vertical axis represents the prediction accuracy, with the lower the value, the higher the accuracy. The green dotted line is 4G-BPNN (MLP+Qeq), blue is the baseline GNN, orange is the GNN directly predicting the charge and correcting for the electrostatic interaction term, and green is the combination of GNN and Qeq to predict the charge and correct for the electrostatic interaction term.
With regard to the method of predicting charge, predicting charge via Qeq (green) is more accurate than predicting charge directly from each atom’s descriptor (orange). This is a trend reported in the 4G-BPNN paper, and it is believed that even for GNNs, it is difficult to solve the task of predicting charge using only local information, and the methods that consider the entire structure, such as Qeq, are more effective.
On the other hand, the baseline model which does not consider the charge was the most accurate except the Ag cluster dataset. Also, all of the baseline accuracies are better than those of 4G-BPNN, probably because MLP can only consider atoms within a certain cutoff radius, and the charge prediction and electrostatic interaction corrections work to account for the portion beyond that radius. The GNN, on the other hand, can effectively extend the cutoff radius by iterating convolution layers. The GNN seems to include the effect of the electrostatic interaction term in the dataset used here. It is difficult to explain the result of Ag cluster dataset, we believe that the inclusion of electrostatic term in the model may have increased the expressive power of the model and improved prediction accuracy.
Summary and Acknowledgements
In this internship, we implemented a method for incorporating the effects of charge transfer in atomistic simulations and evaluated its effectiveness in GNN-based NNPs. We found that the classical Qeq technique itself contributes to the accuracy of charge prediction, although the technique that was effective in MLP-based NNP cannot be used directly in GNNs.
The internship period took only about a month and a half, a short period of time for the whole process from planning the internship theme to conduct all the experiments and summarize them. But it was a fulfilling internship thanks to the generous support of my mentor, Mr. Nakago, my sub mentor, Mr. Hayashi, and other members of the materials science team. Finally, I would like to take this opportunity to express my gratitude to all of you.
References
[1] Jörg Behler and Michele Parrinello, Generalized Neural-Network Representation of High-Dimensional Potential-Energy Surfaces, [Phys. Rev. Lett. 98, 146401 (2007)](https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.98.146401).
[2] S. Alireza Ghasemi, Albert Hofstetter, Santanu Saha, and Stefan Goedecker, Interatomic potentials for ionic systems with density functional accuracy based on charge densities obtained by a neural network, [Phys. Rev. B 92, 045131 (2015)](https://journals.aps.org/prb/abstract/10.1103/PhysRevB.92.045131).
[3] Zhi Deng, Chi Chen, Xiang-Guo Li and Shyue Ping Ong, An electrostatic spectral neighbor analysis potential for lithium nitride, [Npj Comput. Mater. 5, 75 (2019)](https://www.nature.com/articles/s41524-019-0212-1).
[4] Tsz Wai Ko, Jonas A. Finkler, Stefan Goedecker, and Jörg Behler, A fourth-generation high-dimensional neural network potential with accurate electrostatics including non-local charge transfer, [Nat. Commun. 12, 398 (2021)](https://www.nature.com/articles/s41467-020-20427-2).
[5] Oliver T. Unke, Stefan Chmiela, Michael Gastegger, Kristof T. Schütt, Huziel E. Sauceda, and Klaus-Robert Müller, SpookyNet: Learning Force Fields with Electronic Degrees of Freedom and Nonlocal Effects, [arXiv:2105.00304](https://arxiv.org/abs/2105.00304).
[6] Anthony Stone, [The Theory of Intermolecular Forces](https://global.oup.com/academic/product/the-theory-of-intermolecular-forces-9780199672394?cc=jp&lang=en&) (Oxford University Press, Oxford, 2013).
[7] Simon Batzner, Albert Musaelian, Lixin Sun, Mario Geiger, Jonathan P. Mailoa, Mordechai Kornbluth, Nicola Molinari, Tess E. Smidt, and Boris Kozinsky, SE(3)-Equivariant Graph Neural Networks for Data-Efficient and Accurate Interatomic Potentials, [arxiv:2101.03164](https://arxiv.org/abs/2101.03164).
[8] https://github.com/mir-group/nequip
[9] Nathaniel Thomas, Tess Smidt, Steven Kearnes, Lusann Yang, Li Li, Kai Kohlhoff, and Patrick Riley, Tensor field networks: Rotation- and translation-equivariant neural networks for 3D point clouds, [arXiv:1802.08219](https://arxiv.org/abs/1802.08219).
[10] https://e3nn.org/
[11] http://micro.stanford.edu/mediawiki/images/4/46/Ewald_notes.pdf
[12] Todd R.Gingrich and Mark Wilson, On the Ewald summation of Gaussian charges for the simulation of metallic surfaces, [Chem. Phys. Lett. 500, 1-3, 10 (2010)](https://www.sciencedirect.com/science/article/abs/pii/S0009261410013606?via%3Dihub).
[13] Péter T Kiss, Marcello Sega, and András Baranyai, Efficient Handling of Gaussian Charge Distributions: An Application to Polarizable Molecular Models, [J. Chem. Theory Comput. 10, 12 (2014)](https://pubs.acs.org/doi/10.1021/ct5009069).
[14] Anthony K. Rappe and William A. Goddard III, Charge equilibration for molecular dynamics simulations, [J. Phys. Chem. 95, 8, 3358-3363 (1991)](https://pubs.acs.org/doi/pdf/10.1021/j100161a070).
[15] Christopher E. Wilmer, Ki Chul Kim, and Randall Q. Snurr, An Extended Charge Equilibration Method, [J. Phys. Chem. Lett. 3, 17, 2506-2511 (2012)](https://pubs.acs.org/doi/10.1021/jz3008485).