Blog
Introduction
With the advance of machine learning, machine learning potentials (MLPs) have been intensely developed to achieve both scalability and high accuracy comparable to DFT calculations. In particular, universal MLPs (UMLPs), characterized by their applicability to any materials without limitations on atomic elements, have been rapidly realized in recent years. Since the release of Matbench Discovery benchmark [1], numerous UMLPs have been competing to achieve the highest scores. As from 2024, not only academic institutions but also companies have announced their developed UMLPs one after another, including GNoME (DeepMind), MatterSim (Microsoft), ORB (Orbital), and OMat (META). However, there have been concerns that Matbench Discovery leaderboard is becoming saturated and many UMLPs overfit to the benchmark [2]. Although Matbench Discovery benchmark evaluates potential energies of locally stable crystal structures, many material properties depend on a wider range of potential energy surfaces: for example lattice vibration, diffusion, and chemical reactions.
k_SRME is a recently proposed benchmark suite to evaluate UMLPs specifically for the lattice thermal conductivity (LTC) calculations [3], which has been already referenced from Matbench Discovery leaderboard. LTC is not only an important thermal property in engineering, but also depends on higher-order derivatives of the potential energy surface. Therefore, it requires the smoothness of the potential energy surface around the stable structure for better prediction accuracy, and provides a stricter evaluation for UMLPs. Interestingly, the LTC accuracy does not correlate to the stability accuracy for stable crystal structures in many UMLPs, which experimentally demonstrates the concern of overfitting to the benchmark.
We, Preferred Networks, Inc. (PFN), have been developing our UMLP called PFP ahead of the other companies since 2019. PFP is available on Matlantis™, a SaaS product provided by Preferred Computational Chemistry (PFCC), co-developed by PFN and ENEOS Corporation (ENEOS). Matlantis™ is currently used by over 100 organizations and has demonstrated high universality without fine-tuning and limitations on material fields.
In this post, we evaluate PFP v6 using the k_SRME benchmark suite. As shown in Results section, we demonstrate that PFP v6 shows a high accuracy even in the high-order derivatives of the potential energy surfaces. Note that the PFP v6 was released in April 2024, prior to the public release of the k_SRME benchmark suite. Thus, there is no way for the PFP v6 to overfit the benchmark dataset.
Benchmark setting
We provide an overview the computational method for calculating LTC and datasets in the k_SRME benchmark suite [3]. This uses phono3py to calculate the LTC via the relaxation time approximation. The phonon-phonon interaction is derived from the second- and third-order force constants obtained by the supercell method with finite displacements. The LTC predictions are subsequently compared to the DFT calculation results of the PhononDB-PBE dataset, which contains 103 binary compounds similar to PhononDB.
For the LTC calculation, we used most of the default settings: a two-stage relax with FIRE, FrechetCellFilter, fmax=1e-4, and max_steps=300. Notably, we observed that the displacement for the force constant calculation significantly impacts the final LTC result for UMLPs. Therefore, we evaluated two different displacement distances: 0.03 Å (default) and 0.1 Å.
Results
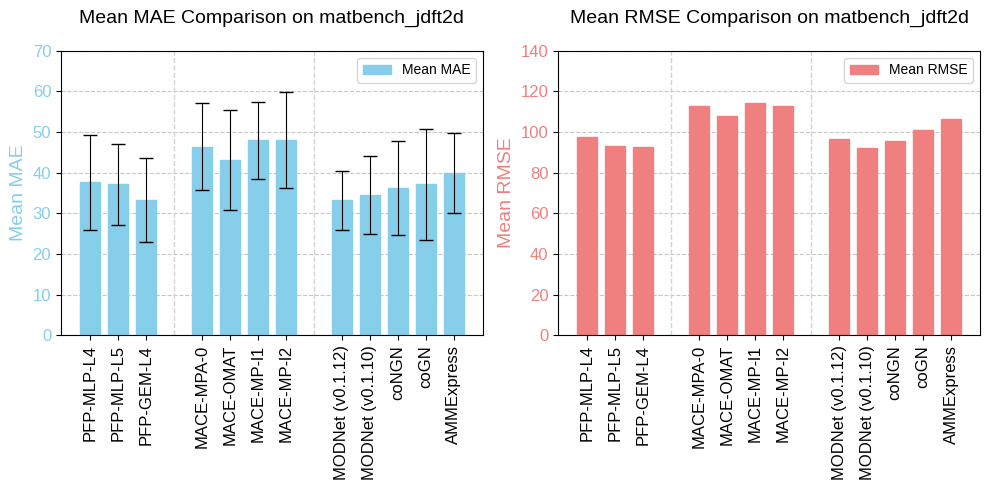
Table 1 presents the LTC calculation errors for PFP v6 and compares the results with those for MACE-L and MatterSim-v1. The LTC calculation errors are quantified by mean Symmetric Relative Error (mSRE) of total macroscopic LTC and mean Symmetric Relative Mean Error (mSRME) of each phonon, as defined in Ref. [3]. Our calculations for MACE-L and MatterSim-v1 with distance 0.03 Å are comparable to the original results. Also, the result shows the higher displacement distance (0.1 Å) generally improves the LTC calculation results of UMLPs, and PFP v6 especially benefits from it. PFP v6 with distance 0.1 Å outperforms the other UMLPs, achieving mSRME 0.374 (cf. the current top model in the matbench discovery leaderboard is MACE-MPA-0 with mSRME 0.412).
Table 1: Lattice thermal conductivity calculation performances in PhononDB-PBE dataset
| mSRE (↓) | mSRME (↓) | |
| PFP v6 (distance 0.03 Å) | 0.530 | 0.656 |
| PFP v6 (distance 0.1 Å) | 0.245 | 0.374 |
| MACE-L (Ref.) | 0.710 | 0.935 |
| MACE-L (distance 0.03 Å) | 0.719 | 0.932 |
| MACE-L (distance 0.1 Å) | 0.694 | 0.915 |
| MatterSim-v1 (Ref.) | 0.413 | 0.575 |
| MatterSim-v1 (distance 0.03 Å) | 0.413 | 0.575 |
| MatterSim-v1 (distance 0.1 Å) | 0.366 | 0.541 |
Figure 1 shows a comparison between LTC at 300 K calculated by PFP v6 with distance 0.1 Å and DFT calculations in a log-log graph. PFP v6 successfully predicts the LTC up to a factor of 2 for 100 out of 103 compounds (See raw data in metrics.txt).
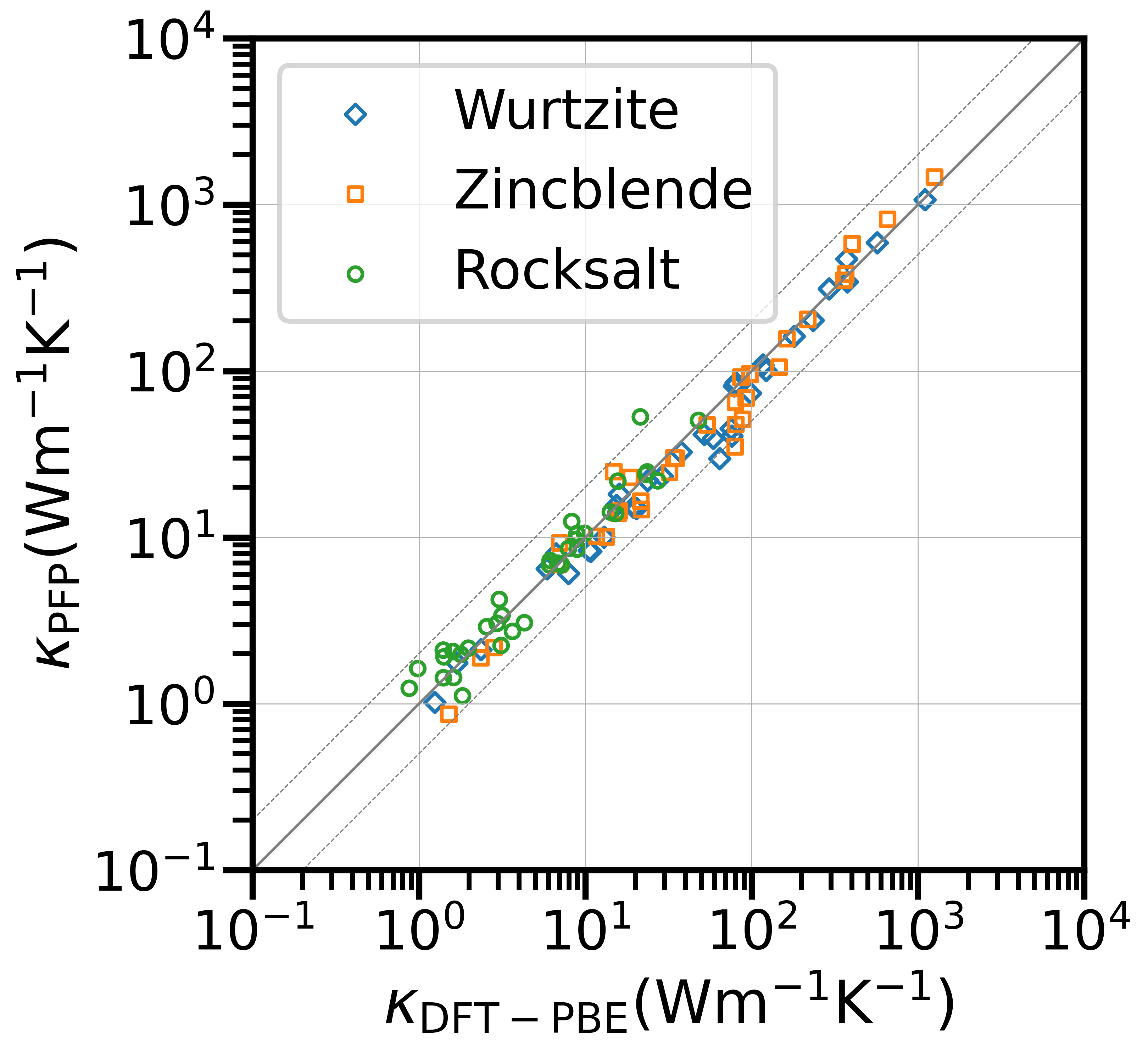
Figure 1: Lattice thermal conductivity at 300 K for structures in PhononDB-PBE dataset with PFP v6 and DFT-PBE. The marker shape and color indicate the prototype structure of the compound, which is one of rocksalt, zincblende, or wurtzite. The solid line indicates perfect agreement, and the dashed lines indicate discrepancies between 50% and 200%.
Error distributions for LTC predictions by PFP v6 are illustrated in Fig. 2. The errors are measured using Symmetric Relative Difference (SRD) [3] for total macroscopic LTC, and SRME for each phonon. As depicted, the displacement distance significantly affects the error distributions.
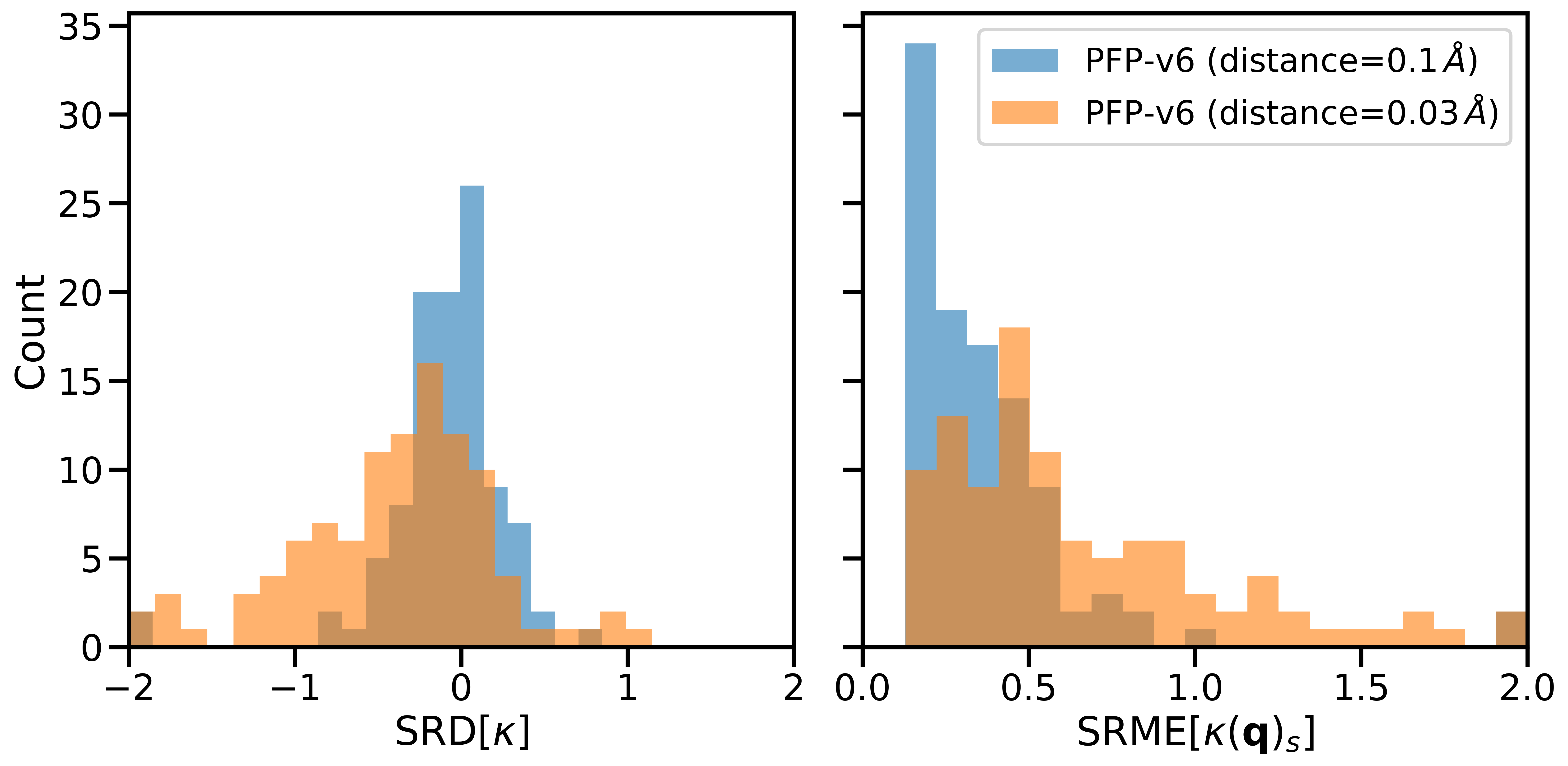
Figure 2: Error distributions of lattice thermal conductivity predictions by PFP v6 for PhononDB-PBE dataset.
Conclusion
PFP v6 achieves current state-of-the-art in the challenging benchmark for lattice thermal conductivity prediction. Although a displacement distance of 0.1 Å is somewhat larger than a typical value used in DFT calculations, most UMLPs prefer the larger displacement distance to avoid generating imaginary modes in locally stable structures. This tendency may provide a clue for further improving the performance of UMLPs.
Note: PFP v6 was developed using the National Institute of Advanced Industrial Science and Technology’s AI Bridging Cloud Infrastructure (ABCI) in addition to PFN’s in-house supercomputers.
[1]: J. Riebesell et al., Matbench Discovery — A framework to evaluate machine learning crystal stability predictions, arxiv:2308.14920
[3]: B. Póta et al., Thermal Conductivity Predictions with Foundation Atomistic Models, arxiv:2408.00755