Blog
Introduction
Machine Learning Potentials (MLPs) are attracting attention for atomistic simulations that combine the accuracy of DFT calculations with the scalability of empirical potentials. Recently, the development of Universal Machine Learning Potentials (UMLPs), which can be applied to various materials regardless of the elements, has been actively pursued. Not only academic institutions but also companies such as Google DeepMind, Microsoft, Orbital, and Meta have announced their own UMLPs. We, Preferred Networks, Inc. (PFN), have been developing our UMLP called PFP ahead of the other companies since 2019. PFP is available on Matlantis™, a SaaS product provided by Preferred Computational Chemistry (PFCC), co-developed by PFN and ENEOS Corporation (ENEOS). Matlantis™ is currently used by over 100 organizations and has demonstrated high universality without fine-tuning and limitations on material fields.
Although UMLPs have been successfully applied to various systems, including catalytic materials, their application limits depend heavily on the model architecture and the DFT calculation dataset used for training, and thus remain unclear. Therefore, the need for benchmarking UMLP performance is increasing. The Matbench Discovery is widely known as a benchmark for UMLPs, aiming to evaluate the energetic properties of inorganic crystal structures. However, even in the inorganic systems, there are many engineering-important systems which are deviate significantly from ideal bulk crystal structures. For example, non-uniform structures such as surfaces, interfaces, and defects have unique energetic properties that arise from their special chemical states, and those structures often play critical role in material processes.
In this context, CHIPS-FF (arxiv, github) has been recently proposed as an automatic benchmarking tool to evaluate the accuracy of UMLPs for a wide range of physical properties, including surface energy and defect formation energy. The paper comprehensively benchmarks major UMLPs such as ALIGNN-FF, CHGNet, M3GNet, ORB, SevenNet, MACE, eqV2 (OMat24), and MatterSim for 103 materials primarily used as semiconductor device materials.
In this post, we evaluated the performance of PFP v7 for surface energy using CHIPS-FF [1]. As shown in Result section, we demonstrated that PFP v7 shows high accuracy in evaluating surface energy. Note that PFP v7 is a model released in September 2024, before the public release of CHIPS-FF, and was not fine-tuned for this specific purpose.
Benchmarking Setup
We explain the surface modeling, surface energy calculation method, and dataset overview in CHIPS-FF. Following the surface modeling in the CHIPS-FF task, we selected non-polar surfaces from (100), (111), (110), (011), (001), and (010) to create slabs (surface structures). The slab models consist of at least 4 layers of atoms and 18 Å thick vacuum layers, stacked alternately under periodic boundary conditions. The surface energy is evaluated by the following equation:
$$ \gamma=\frac{E_\mathrm{surface}-N \cdot E_\mathrm{bulk}}{2A} $$
where \(E_\mathrm{surface} \) is the energy of the surface structure, \(E_\mathrm{bulk}\) is the energy of the bulk structure per unit cell, \(N\) is the number of unit cells in the surface structure, and \(A\) is the surface area of the top and bottom surfaces.
We used the CHIPS-FF Surface Energy Dataset for the dataset. Specifically, we compared the surface energy of 85 non-polar surfaces for 46 compounds with the DFT calculation results in the CHIPS-FF Surface Energy Dataset. It should be noted that the CHIPS-FF Surface Energy Dataset uses vdW-DF-OptB88, one of the van der Waals density functionals that take account of dispersion force.
For structural relaxation, we used the FIRE optimization algorithm with FrechetCellFilter, fmax=0.05, and max_steps=200. The initial bulk structures were obtained from JARVIS-DFT. We found that whether to consider an empirical dispersion correction, D3 correction, significantly affects the results in surface energy calculations. Therefore we verified with two calculation modes: with and without the D3 correction [2]. We examined the two PFP models, v7 and v6, and confirmed that similar results were obtained, so we only present the results of PFP v7 in this post.
Results
Table 1 shows the surface energy errors of PFP v7 without D3 correction and other UMLPs (ORB [3], eqV2 from OMat24 [4], MatterSim-v1 [5], MACE-MPA-0 [6]). The errors are quantified by Mean Absolute Error (MAE). PFP v7 shows surface energy prediction performance (MAE: 0.19) comparable to the best-performing models, ORB (orb-v2 MAE: 0.18) and eqV2 (MAE: 0.17-0.20). Considering the UMLPs and the approximation error of DFT calculations to experimental values [7] (Standard error: ±0.27 J/m²), the error of PFP (MAE: 0.19) is in the discrepancy range between DFT calculation and the real world, and PFP v7 achieved enough accuracy to reproduce DFT calculation. In the recently posted “Lattice Thermal Conductivity Calculation with PFP“, it was also reported that PFP showed the best score in the benchmark of lattice thermal conductivity. Specifically, PFP v6 (distance=0.1 Å) showed an excellent result of mSRME 0.374, while ORB and eqV2 were the models with the largest errors [8]. It is also interesting that MatterSim-v1 and MACE-MPA-0, which showed high scores in the lattice thermal conductivity benchmark, did not show good scores in this surface energy benchmark since their errors are out of the discrepancy range between DFT calculation and the real world. This highlights the importance of comprehensive benchmarking rather than relying on a single indicator.
Table 1: Surface energy prediction accuracy of PFP v7 and other UMLP models in the CHIPS-FF Surface Energy Dataset. The results of other UMLP models are quoted from the CHIPS-FF paper [9].
| Model name | MAE (J/m²) |
| PFP v7 | 0.19 |
| eqV2_31M_omat_mp_salex | 0.17 |
| eqV2_31M_omat | 0.18 |
| eqV2_86M_omat_mp_salex | 0.18 |
| eqV2_153M_omat | 0.19 |
| eqV2_86M_omat | 0.20 |
| orb-v2 | 0.18 |
| MatterSim-v1 | 0.36 |
| MACE-MPA-0 | 0.33 |
In order to clarify the causes of error in surface energy, we present a parity plot between PFP v7 and DFT in Figure 1. Generally, PFP v7 shows good agreement with DFT results, but PFP v7 without D3 correction tends to underestimate the DFT results, while PFP v7 with D3 correction tends to overestimate the DFT results. Similar trends are reported in the original CHIPS-FF paper when comparing the results of orb-v2 and orb-d3-v2 (orb-v2 with D3 correction). This systematic error is considered to be due to the difference in functionals used, as the PFP v7 training dataset uses the PBE functional, while the CHIPS-FF Surface Energy Dataset uses vdW-DF-OptB88. Also in previous study [10] comparing the surface energies of metals using PBE, PBE-D2, and vdW-DF-OptB86b has demonstrated the general trend where the surface energy changes in the order of PBE < vdW-DF < PBE-D, which is consistent with our results [11]. Therefore, the main factor contributing to the discrepancies is the difference in functionals, and it is expected that using the same functional for comparison will yield results that are much closer to the DFT calculation.
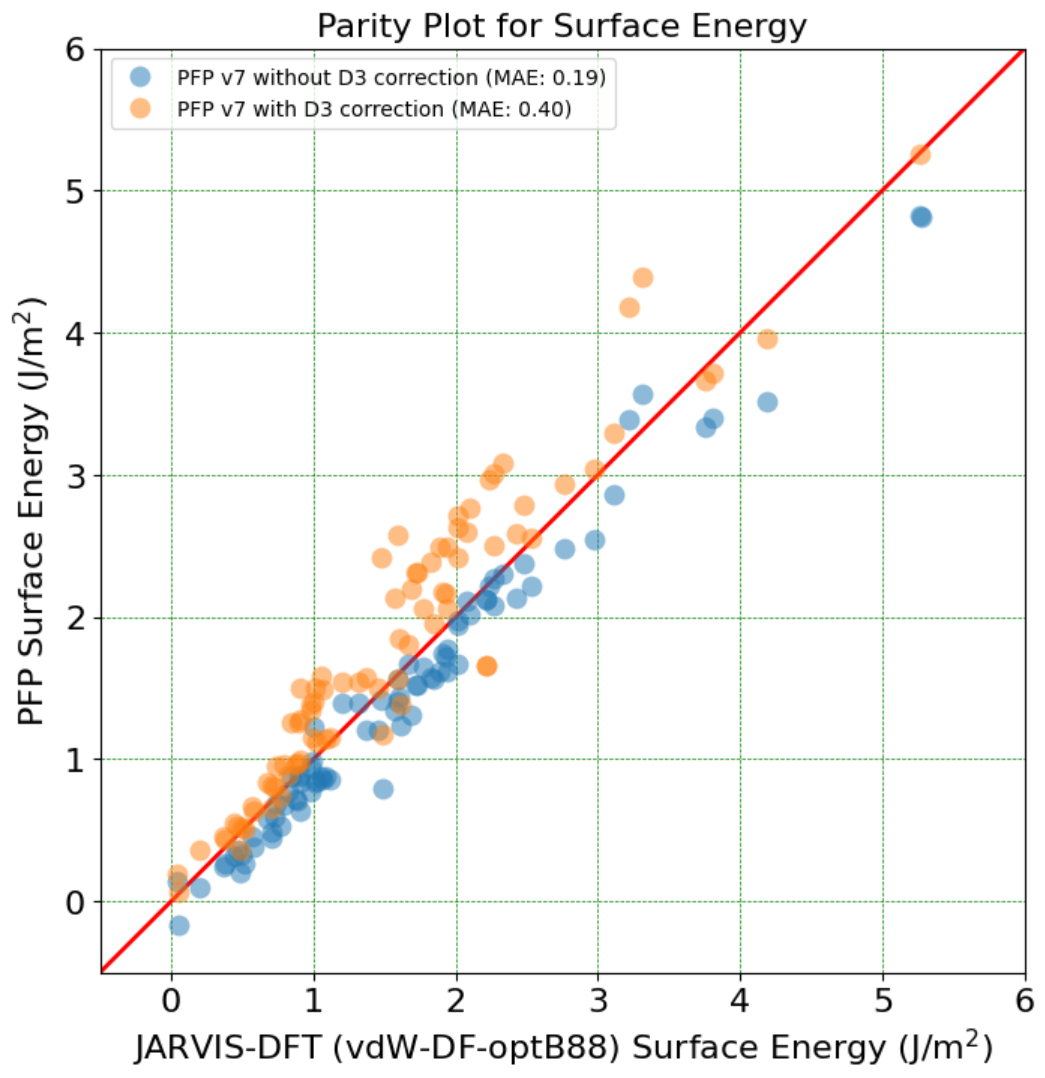
Figure 1: Comparison of surface energy between PFP v7 and DFT in the CHIPS-FF Surface Energy Dataset
Conclusion
We demonstrate that the PFP v7 predicts surface energy with MAE of 0.19 J/m², which is comparable to the best-performing models. Considering the systematic error caused by the functional difference used in the training dataset of UMLPs and the CHIPS-FF Surface Energy Dataset, the accuracy seems to saturate around 0.2 J/m², which results in PFP v7 having very similar performance to other models. Furthermore, the consistently high performance of PFP in the recent benchmark for lattice thermal conductivity, which ORB and eqV2 fail to predict well, validates its reliability and versatility. These findings highlight PFP as a superior choice for researchers and engineers seeking a more comprehensive solution for materials discovery.
Note: PFP v7 was developed using the National Institute of Advanced Industrial Science and Technology’s AI Bridging Cloud Infrastructure (ABCI) in addition to PFN’s in-house supercomputers.