Blog
本記事は、2023年夏季インターンシッププログラムで勤務された佐々木司温さんによる寄稿です。
目次
- 概要
- 背景
- 先行研究
- 再現実験
- 考察&改善案
- まとめ
- おわりに
- 参考文献
概要
今回のインターンでは、LLM関連の技術領域であるRetrieval Augmented Generation(RAG)について、REPLUG(-LSR)[1]という手法の再現に取り組みました。
最終的にREPLUGについては論文と同様の結果を得ることができましたが、REPLUG-LSRに関しては論文通りの結果とはなりませんでした。実際に取り組んでいる中での難しさ、発見について共有したいと思います。
背景
現在(2023年)LLMが非常に注目されていますが、その活用には様々なハードルがあります。その内の1つとして、ハルシネーション(Hallucination:幻覚)があります。ハルシネーションとは、もっともらしい嘘(=事実とは異なる内容や、文脈と無関係な内容)の出力が生成されることです。この課題に対しての対応策としてRAGがあります。
RAGは、LLMが持つ知識や推論能力を補うために、外部の知識ソースを何かしらの形式で入力に追加し、LLMが生成する回答の質の向上を試みるフレームワークです。
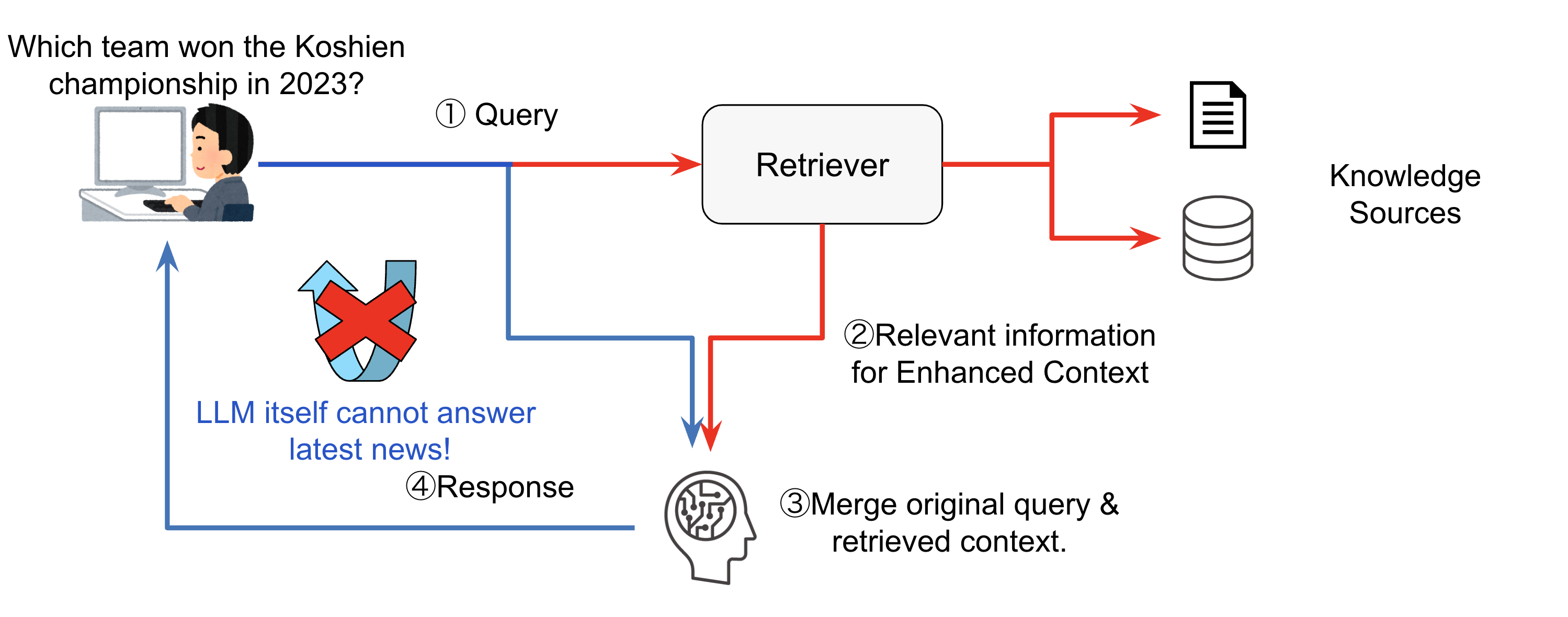
RAGの利点として、LLMが最新の情報にアクセスできることと、ユーザがLLMの入力に使用された外部ソースを参照でき、出力の妥当性を検証できることが挙げられます。
RAGのフレームワークにおいて、考慮すべき事項として
- クエリに関連する情報をどのように検索するか?
- クエリとは関係のない文書を追加で入力した場合、ノイズを入力に追加することになり、精度の低下が考えられる。
- 検索結果をどのような形式でLLMに入力(前処理・後処理)するか?
- クエリに情報を付加 ex) REPLUG
- LLMの出力の調整(next tokenの確率分布の調整)
- LLMの中間表現の修正 ex) RETRO[2]
- どのようなLLMを使用するか?
- 学習対象はRetriever (与えられたクエリ文書に近い文書を取ってくるための機構) なのか、LLMなのか、両方なのか?
が挙げられます。
今回再現の対象とするREPLUGの特徴として、LLMをブラックボックスとして扱うことができ、事前学習した Retriever モデルをそのまま使うこともできる一方、より高い性能を得るために Retriever 側に追加学習を施すことも可能という点があります。LLMのアーキテクチャの変更や、追加での学習には非常にコストがかかるので、比較的手軽な手法になります。一方で、手軽な手法であるため、精度の向上もそこまでないのでは?と思われるかもしれませんが、bits per UTF-8 encoded byte(BPB)という評価指標において提案論文で、GPT3では6.3%、five-shot MMLU Codexでは 5.1%、それぞれREPLUG無しと比べて改善しています。
実際に論文と同等の精度が向上するのか?ということで実際に再現実装および検証をしました。
先行研究
再現の対象である、REPLUGおよびREPLUG-LSR[1]について簡単に紹介します。詳細については論文を読んで頂ければと思います。また、自然言語の埋め込みの獲得や利用については、この動画[3]が非常に参考になると思います。
REPLUG の特徴
- クエリに関連する情報をどのように検索するか?
- Bi-encoderによるEmbeddingベクトルのpairのcos類似度に基づいて検索
具体的な流れについては以下の通りになります。
query → Bi-encoderによるEmbeddingベクトルの計算 → 事前に計算しておいた参照用ドキュメントのEmbeddingベクトルと比較 → 類似度の高いtop kのドキュメントを取得
- Bi-encoderによるEmbeddingベクトルのpairのcos類似度に基づいて検索
- 検索結果をどのような形式でLLMに入力(前処理・後処理)するか?
- 検索結果のドキュメント毎に、クエリを後ろに独立に結合
- クエリと検索結果のドキュメント間の類似度に基づいて重みを計算
- 結合したドキュメントをLLMに入力し、next tokenの確率分布を前述の重みで、重み付け平均を計算し、この分布をqueryに対する出力とする。
- どのようなLLMを使用するか?
- 自由に選べる。今回は主にGPT2 small[4]を使用。
- 学習対象はRetrieverなのか、LLMなのか、両方なのか?
- なし
利点
- 検索結果のdocumentの数を増やしても、LLMへの入力は、検索結果ドキュメントの長さの最大長分しか増えない
- context sizeをあまり圧迫しない。
不利点
- 検索結果の数と同じ回数LLMの推論を行わなければならない。
以下の図もご参照ください。(論文 [1] から引用)
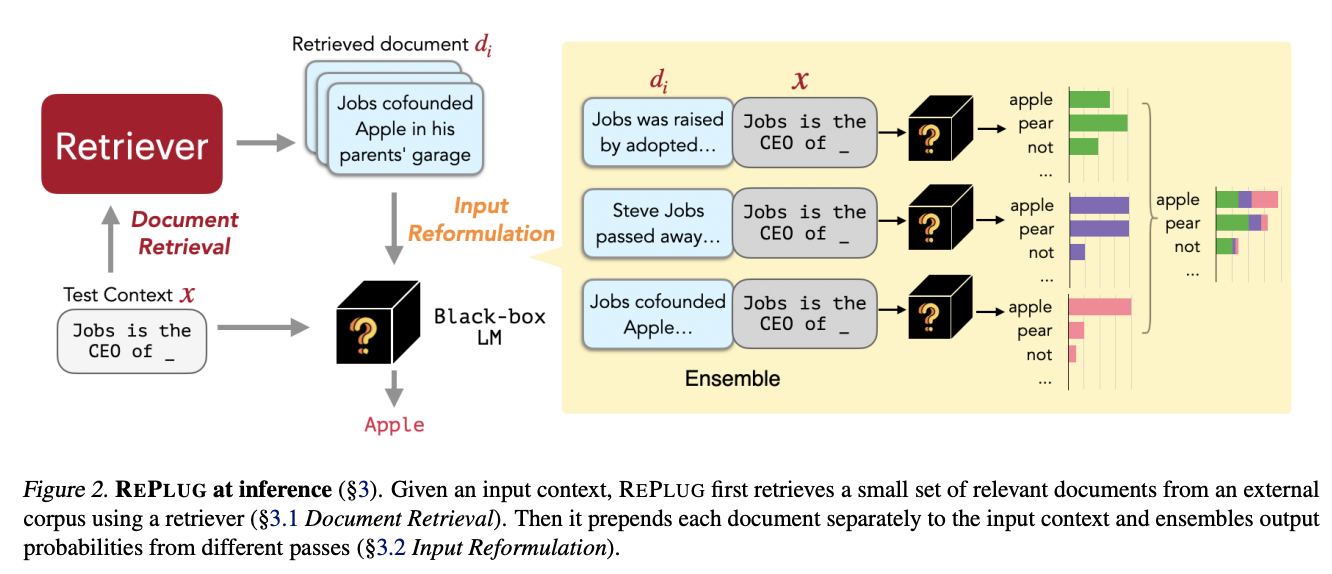
読み飛ばしても問題ないのですが、数式としては以下のようになります。
推論(next token prediction)
\(p(y | x, D’) = \sum_{d \in D’} p(y | d \circ x) \cdot \lambda(d, x) \)
ただし、ノーテーションは以下の通りとします。
| \(\mathcal{D} = \{d_1, …, d_m\}\) | 全ドキュメントの集合 |
| \(d \in \mathcal{D}\) | ドキュメント |
| \(\textrm{E}(d)\) | ドキュメントのembedding |
| \(s(d, x) = cossim(\textrm{E}(d), \textrm{E}(x))\) | \(d,x \) の類似度 |
| \(\mathcal{D’} \subseteq \mathcal{D}\) | 一部のドキュメントの集合 |
| \(d1 \circ d2\) | \(d1, d2\) の結合 |
| \(p(y | d) = P_{LM}(y | d)\) | \(d\)を入力したとき言語モデルの\(y\)の予測確率 |
| \(\lambda(d, x) = \frac{e^{s(d, x)}}{\sum_{d \in D’} e^{s(d, x)}}\) | \(x\)に対する\(d\)の\(D’\)内での相対的な類似度 |
| \(B\) | バッチサイズ |
REPLUG-LSRの特徴
基本的には前述のREPLUGと同様ですが、学習可能パラメータが存在することが違いになっています。
- 学習対象はRetrieverなのか、LLMなのか、両方なのか?
- Retriever
推論の方法はREPLUGと同様になります。
REPLUG-LSRの学習方法について
REPLUG-LSRでは、検索結果のドキュメントの相対的なスコアをLLMが評価し、その評価値の分布に近づくように検索を修正します(下図参照)。検索はBi-encoderによるEmbeddingに基づいているので、実質的にはBi-encoder modelが更新されます。
LLMの推論に役に立つような良いドキュメントはより、クエリと結びつきやすくするイメージになります。
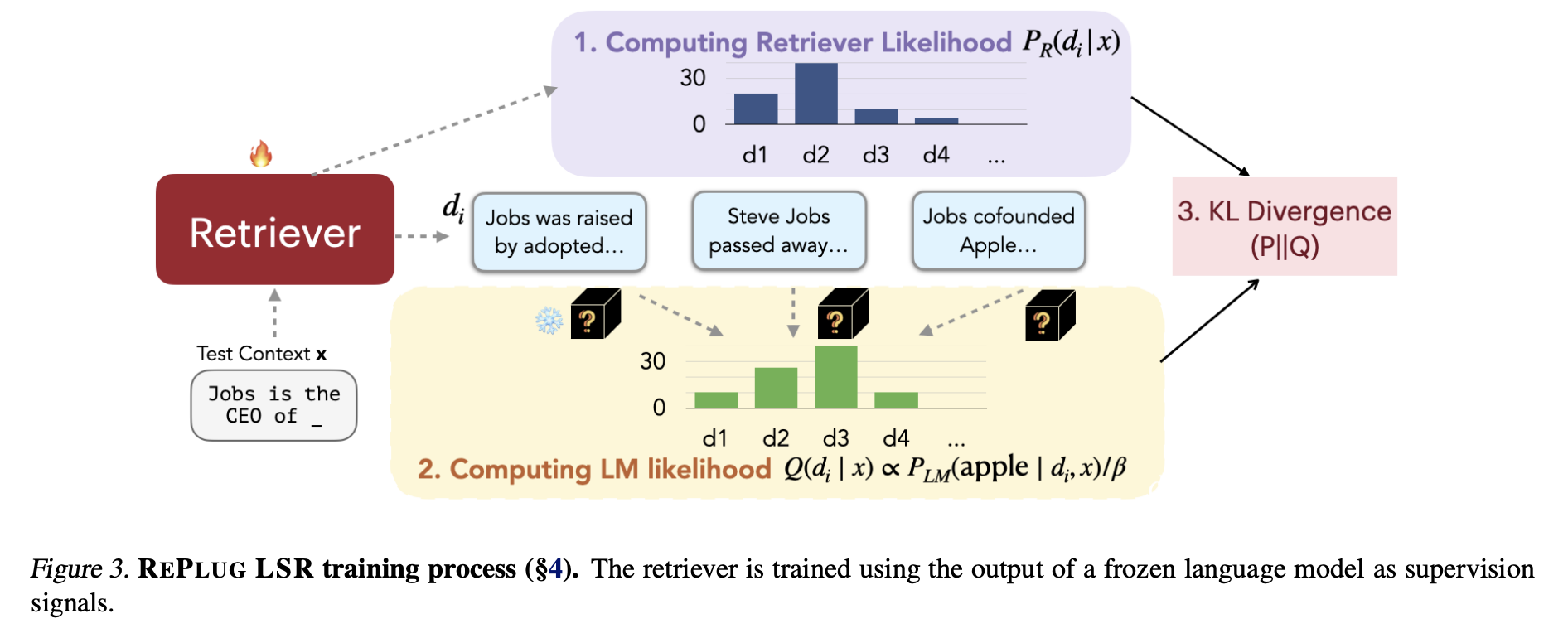
([1] から引用)
数式としては、
Retrieval likelihoodとLM likelihoodとの間でのKL divergenceをとります。
Retrieval likelihoodは
$$P_R(d | x) = \frac{e^{s(d, x)/\gamma}}{\sum_{d \in D’} e^{s(d, x)/\gamma}}$$
LM likelihoodは、next token yを用いて
$$Q_{LM}(d | x, y) = \frac
{e^{P_{LM} (y | d, x) / \beta}}
{\sum_{d \in D’} e^{P_{LM} (y | d, x) / \beta}}
$$
ただし,
$$ P_{LM} (y | d, x) \equiv P_{LM} (y | d \circ x)$$
損失関数は、
$$\mathcal{L} = \frac{1}{|B|} \sum_{x \in B} KL(P_R(d|x) || Q_{LM}(d | x, y))$$
となります。
再現実験
実際に論文に沿ってREPLUGを実装して、小さいデータセットで検証した結果を以下に示します。
| 実験のパラメータ | |
| チャンクサイズ | 256 tokens |
| 検索対象のトークン数 | 68.8 M (268 k chunks) |
| 評価用クエリのトークン数 | 6.88 M (26.8 k chunk) |
| LLM | GPT2 small |
| Retriever | 事前学習済みBERT[5](bert base uncased)をmean poolingしたembedding + cos類似度で検索 |
| \(\|D’\|=\)topk | 10 |
また、REPLUG-LSRに関しては以下のパラメータで実装しました。
| 実験のパラメータ | |
| チャンクサイズ | 256 tokens |
| 検索対象のトークン数 | 68.8 M (268 k chunks) |
| 学習用トークン数 | 55.0 M (215 k chunk) |
| 評価用クエリのトークン数 | 6.88 M (26.8 k chunk) |
| LLM | GPT2 small |
| Retriever | 事前学習済みBERT[5](bert base uncased)をmean poolingしたembedding + cos類似度で検索 |
| \(\|D’\|=\)topk | 10 |
| Optimizer | Adam[6] |
| Learning rate | 2e-5 |
| Scheduler | Linear Warmup(2 epoch), Cosine Annealing[7] |
| Epoch数 | 20 |
| 検索対象embeddingの更新 | 3000 iteration毎 |
結果は以下の通りになります。
| GPT2 small | REPLUG (GPT2 small, BERT) | REPLUG-LSR (GPT2 small, BERT) | |
| Perplexity(PPL) | 26.3968 | 24.2812 | 24.4536 |
| PIQA (acc / norm acc) | 0.6289/0.6251 | 0.6279/0.6262 | 0.6235/0.6273 |
REPLUG-LSRは論文を参考にして実験をしたのですが、単純な実装ではPPLがREPLUGよりやや悪化し、論文の結果とは一致しませんでした。
考察&改善案
PPL↓, PIQAほぼ変化なし
PPLに関しては改善が見られましたが、PIQAに関してはREPLUGの有無による変化は見られませんでした。
仮説として、
- PPLが下がるのは、LLMが検索してきた文書とクエリとの表面的な単語の共起関係を見ているから。本質的に文書の内容を理解していない
- 検索してきた文書のトークン長が長く、クエリに関する情報と関連する部分がほんの一部になっており、冗長になっている。結果として、冗長な部分がノイズとして作用している。(参考: RETRO 64 token, REPLUG 128 token)
が考えられます。
対応策としては、
- 性能が良いLLMを使う
- 検索対象の文書の分割サイズを小さくする
が考えられます。
REPLUG-LSRの学習があまり上手くいかない原因については、
LLM likelihoodがほぼ一様分布になっていることが考えられます。
LLM likelihoodとRetrieve likelihoodの間でKL divergenceをとっているため、Retrieve likelihoodが一様分布になるように学習が進みます。
Retrieve likelihoodが一様分布になる条件を満たすEmbeddingとして、定数ベクトルが考えられます。どのようなクエリに対しても同じ検索結果になってしまうので、検索の意味がなくなってしまいます。
また、Vector Storeの更新をしてから学習を進めていく中で、学習中のモデルによるクエリのEmbeddingでVector Storeへ検索をかけるとcos類似度が段々と下がっていく現象が見られました。Vector Storeを更新するとcos類似度が0.9以上に戻るのですが、どうしてこのような現象が起きるのかについては原因はわかっていません。
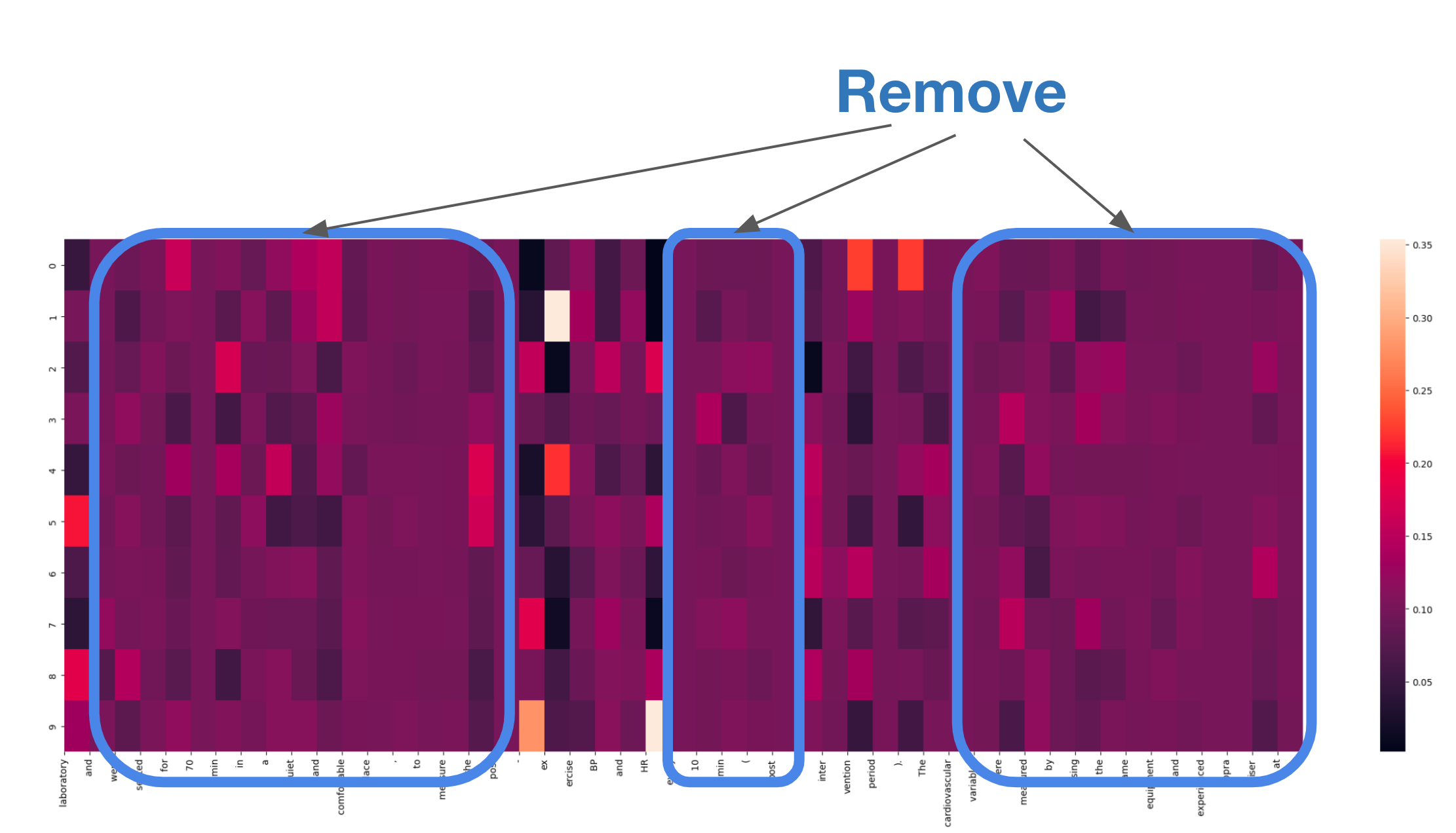
あるクエリに対して、検索をかけて10個の文書をとってきたときのLLM likelihood \(Q_{LM}(d | x, y)\)を以下に示します。
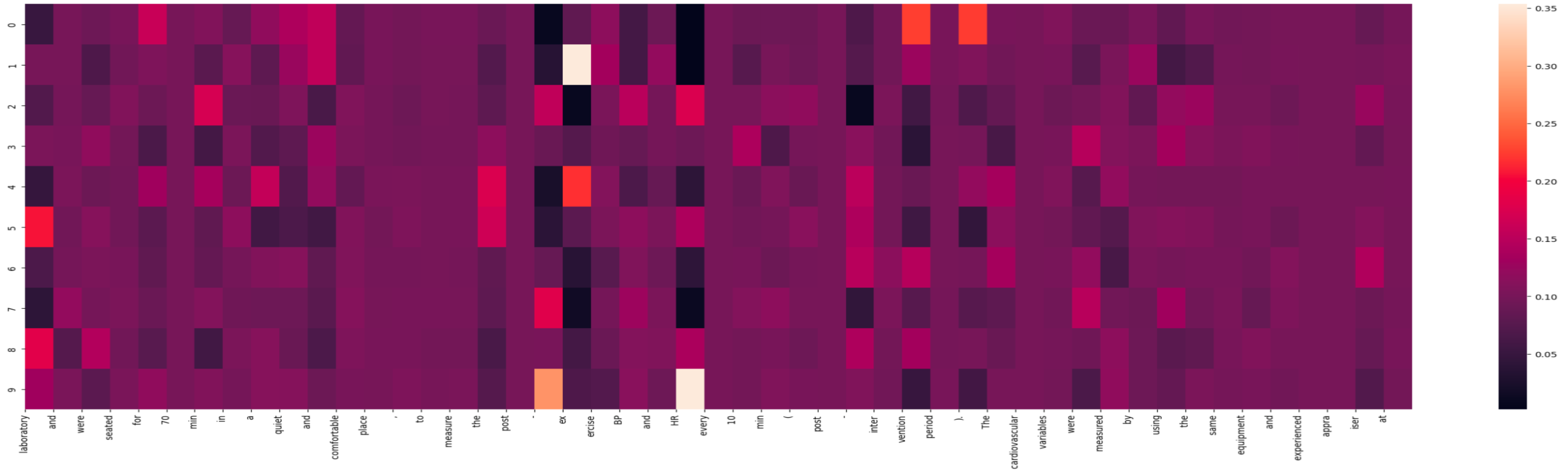
(この図で使っている文章は、H. Arazi らによる論文 Cardiovascular responses to plyometric exercise are affected by workload in athletesの一節を使用しています)
x軸がqueryになっていて、y軸がとってきたdocumentの通し番号になります。LLM likelihoodの特性上、各列で縦方向に和をとると1になります。系列の大半の部分でLLM likelihoodが一様分布に近いことが伺えます。検索結果のドキュメントの評価をするにあたって、実際に注目して欲しいのは、この例ではHRなどの文書固有と思われるトークンになります。
これらの問題に対して、以下の改善策を講じました。
- LLMによる評価が一様にならないようにする
- エントロピーに基づくフィルタリング
- term frequency(tf)による重みづけ
- 事前学習済みのBERTのEmbeddingの、多様性を失わないようにさせる
- ランダムサンプリング
- 事前学習済みのモデルによるクエリと検索結果のドキュメントの相対的な関係と、学習中のモデルによるクエリと検索結果のドキュメントの相対的な関係を保存するような項の追加
エントロピーに基づくフィルタリング
先ほども示した図において、ある列に注目したときに一様分布に近い場合は無視することを考えます。一様に近いかどうかをエントロピーを用いて評価します。ここでは、各列においてエントロピーを計算し、下位10%の列のみ計算対象としました。
term frequency(tf)による重みづけ
頻出する単語(is, a, the, I, youなど)に関しては、検索してとってきた文書が大きく寄与することはあまりなさそうなので、そのような単語のLLM likelihoodへの寄与は小さくしたいです。ここで、LLM likelihoodはQueryの各位置においてのtfによる重み付け和とします。
$$
Q_{LM}(d | x, y) = \sum_{t}^{window\hspace{1pt}size} \lambda_{y_t} P_{LM}(y_t | d, x)
$$
但し、
$$
\frac{1}{\lambda_i} \propto tf(i)
$$
$$
\sum_{d \in D’} Q_{LM}(d | x, y) = 1
$$
とする。
これによってLLMの評価が一様分布に近づくことを回避します。
ランダムサンプリング
REPLUG-LSRの損失関数は、対照学習においてよく使われる損失と類似しています。対照学習ではハードネガティブと呼ばれるサンプルを適切に選ぶことが学習をする上で非常に重要です。REPLUG-LSRにおいては、LLMの予測に寄与しないドキュメントが検索結果に入っていた場合、役に立たないので検索結果に出てこないでねとRetrieverに教えることに相当します。今回は検索結果に、検索対象のドキュメントからランダムにサンプルしたものを追加しました。
事前学習済みのモデルによるクエリと検索結果のドキュメントの相対的な関係と、学習中のモデルによるクエリと検索結果のドキュメントの相対的な関係を保存するような項の追加
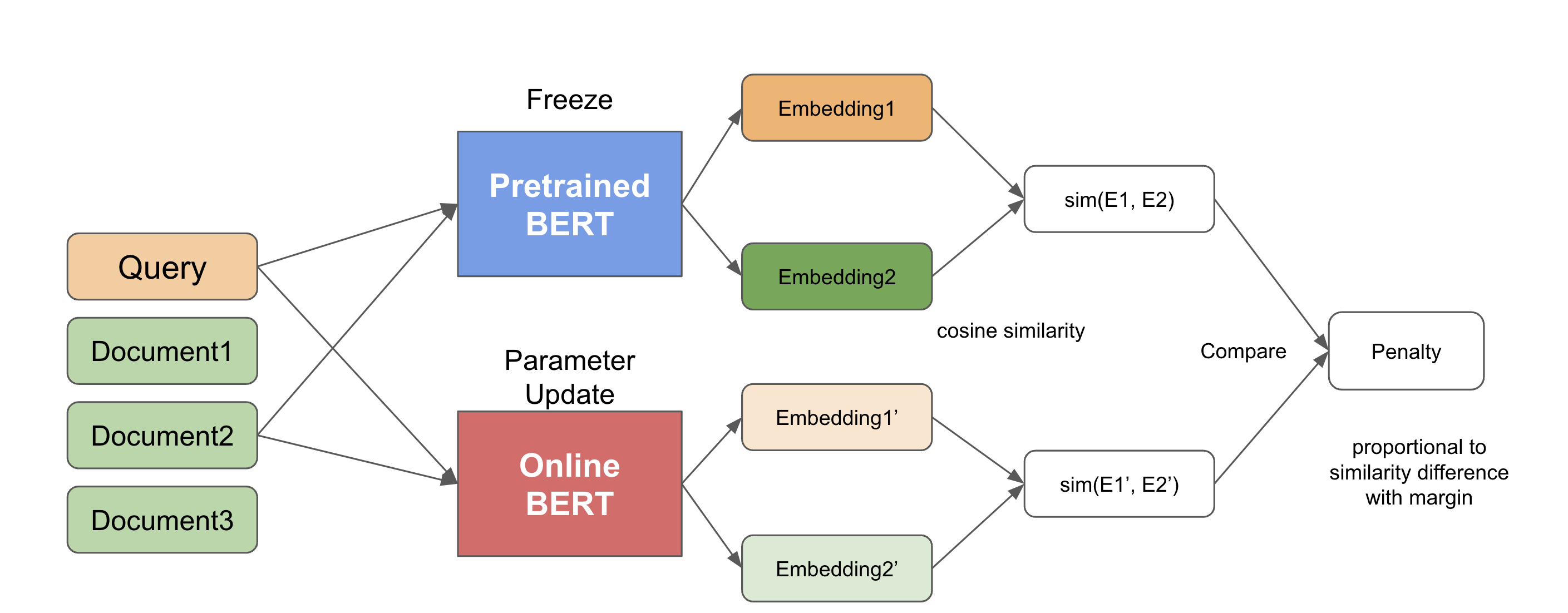
数式としては以下の通りになります。
$$
\begin{align*}
ReLU(|cossim(\textrm{E}(d), \textrm{E}(x)) – cossim(\textrm{E}_{orig}(d), \textrm{E}_{orig}(x))| – m)
\end{align*}
$$
ただし、
$$
\textrm{E}_{orig}: 事前学習済みのBERT
$$
ただし、この項は埋め込み結果が事前学習済みモデルから大きく離れてしまい、大域的な埋め込みの構造が破壊されることを避けるためのものです。実際に context として与えたときに推論結果を改善できないような書類を取ってくることに対して直接ペナルティをかけるわけではないことに注意してください。
改善案の実験結果
以下に改善案の実験結果を示します。全てのハイパーパラメータを探索することは困難だったので、一部抜粋しています。PIQAについては、後述の通りあまり精度がなかったので一部評価を省略しています。
| Model type | LLM beta | Coherency loss | Random replace | Entropy filtering | tf weighting | perplexity(PPL) | PIQA acc | PIQA norm acc |
| REPLUG-LSR | 0.1 | ✅ | 2 | ✅ | ✅ | 24.02 | – | – |
| REPLUG-LSR | 0.5 | ✅ | 0 | ✅ | ✅ | 24.02 | 0.6245 | 0.6235 |
| REPLUG-LSR | 0.5 | ✅ | 0 | ✅ | ✅ | 24.03 | 0.6213 | 0.6311 |
| REPLUG-LSR | 0.5 | ✅ | 0 | ✅ | ✅ | 24.06 | – | – |
| REPLUG-LSR | 0.1 | ✅ | 0 | ✅ | ✅ | 24.06 | – | – |
| REPLUG-LSR | 0.5 | ❌ | 0 | ✅ | ✅ | 24.68 | 0.6300 | 0.6273 |
| REPLUG-LSR | 0.1 | ❌ | 0 | ✅ | ✅ | 24.69 | 0.6159 | 0.6251 |
| REPLUG-LSR | 0.1 | ❌ | 0 | ❌ | ❌ | 24.45 | 0.6235 | 0.6273 |
| REPLUG(GPT2 small, Pretrained BERT) | / | / | / | / | / | 24.28 | 0.6279 | 0.6262 |
| GPT2 small | / | / | / | / | / | 26.40 | 0.6289 | 0.6251 |
表から読み取れるように、
Perplexityに関しては、coherency loss(前述の事前学習済みモデルの相対的なEmbeddingを保存する項)の有無が結果に影響を与えています。一方でエントロピーフィルタリング、tfによる重みづけの少なくとも一方はperplexityに関しては良くない影響を与えていそうです。
今後に向けて
REPLUGのフレームワークにおいて生成の精度を上げるには、Retrieverの改善とLLMの改善があると考えます。ここではRetrieverの改善について述べたいと思います。
類似度、距離の指標の工夫
今回は、Bi-encoderによるEmbedding間のcos類似度を指標として扱いました。これ以外にもEmbedding間の内積を指標として扱う方法なども考えられます。また、よりシンプルなものとしてJaccard係数を指標として使うことも可能です。
学習の工夫
今回の実験では事前学習済みのBERTをしましたが、SimCSEなどで学習されたものに変えるなどの工夫が考えられます。REPLUG-LSRのように学習をする場合は論文で提案されていた損失関数に加えて本来のBERTの事前学習タスクも同時に行うことにより、定数ベクトルを出力することを学習することを回避できると考えられます。また、今回の実験では類似度が高い順からドキュメントを選んでいるので、入力がポジティブサンプルばかりになっている可能性があります。そのためランダムにドキュメントを入れ替えていたのですが、対照学習の文脈で効果的と言われているのが、ハードネガティブサンプルを入力することです。一例として、ベクトル検索をするときにMaximum Marginal Relevance(MMR)を用いて、多様性のある検索結果を得られるようにすることが考えられます。
Retrieved Documentの評価
特にREPLUG-LSRでの枠組みでは、どのドキュメントをとってくるのか、ドキュメントへのフィードバックをどのようにするのか、が非常に重要です。next token predictionの確率の平均などをとっていましたが、クエリ側の尤度または対数尤度に基づいてフィードバックを行うなどの方法が考えられます。
検索の高速化
今回の実装ではcos類似度に基づく検索はfaissのFlatIPを用いました。ただし、FlatIPは全探索を行うのでデータサイズが大きくなるとボトルネックになりかねません。2つのベクトルのcos類似度は、ベクトルの大きさを1に揃えておけば内積で表現でき、L2距離と比例することが簡単な計算でわかります。従って、検索対象ドキュメントのembeddingをクラスタリングしておき、階層的に検索をすることが可能です。この機能自体はfaissのみで実現できるので、より大きいデータセットで検索をする際には試してみる価値があると思います。
まとめ
今回のインターンではREPLUGおよびREPLUG-LSRについて再現実装および改善について取り組みました。結果としては、REPLUGの再現はできたものの、REPLUG-LSRはナイーブな実装ではうまくいきませんでした。また、REPLUG-LSRの学習が上手くいかない理由について、検索されたドキュメントに対するLLM側のフィードバック方法に問題があるのではないかと考え、フィードバック方法や損失関数の工夫をすることで、学習前よりperplexityが下がることが確認できました。
おわりに
自分の専攻が大分異なるというのもあり、NLPに関しての知識が初学者に毛が生えた程度&大きいモデルの学習をしたことがありませんでした。インターンが始まるまで大丈夫かなと心配していたのですが、毎日のミーティングなどで、メンターである村井さん、鈴木さんに非常に手厚くサポートして頂き、なんとかやり遂げることができました。
社員さん同士の会話で、右から左から聞いたことがない単語が飛び交って戸惑う場面もありましたが、勉強していつかその会話に入りたいなとモチベーションになりました。
振り返ってみると非常に密度の高い6週間で、とても楽しく充実した毎日を過ごすことができました。メンターの方をはじめとして、関わって下さった皆さまに感謝申し上げます!本当にありがとうございました!
参考文献
[1] Weijia Shi, et al “REPLUG: Retrieval-Augmented Black-Box Language Models” arXiv:2301.12652
[2] Sebastian Borgeaud, et al “Improving language models by retrieving from trillions of tokens” arXiv:2112.04426
[3] Training State-of-the-Art Text Embedding & Neural Search Models https://youtu.be/XHY-3FzaLGc?si=Gf0CkisX7jy8ly6X
[4] Alec Radford, et al “Language Models are Unsupervised Multitask Learners”
[5] Jacob Devlin, et al “BERT: Pre-training of Deep Bidirectional Transformers for Language Understanding” arXiv:1810.04805
[6] Diederik P. Kingma, Jimmy Ba “Adam: A Method for Stochastic Optimization” arXiv:1412.6980
[7] Ilya Loshchilov, Frank Hutter “SGDR: Stochastic Gradient Descent with Warm Restarts” arXiv:1608.03983




