Blog
本記事は、2023年インターンシップとして勤務した角野祐弥さんによる寄稿です。
2023年度夏季インターンシップに参加させていただいた、角野祐弥です。この度インターンプロジェクトとして、深層学習で学習時のメモリ消費を削減する手法として知られている再計算アルゴリズムの性能向上に取り組みました。成果として、ベンチマークとして用いた全ての学習モデルに対して、既存のアルゴリズムよりさらに省メモリかつ実行時間のオーバーヘッドが少なくなるような性能向上に成功しましたので、その取り組みと成果について、ここでご紹介させていただきます。
背景
今日ではニューラルネットワークは産業の様々な分野で使われており、より大規模なモデルが開発され続けています。ここでの大規模なモデルとはパラメータやレイヤの数が多いモデルのことであり、このようなモデルは学習時に非常に多くのメモリを使用します。モデルの学習時に使用メモリがGPU 1台のメモリに収まらない場合、しばしばデータのバッチサイズを小さくしたり、量子化して消費メモリを下げるといった手法がとられますが、こうした方法ではモデルの出力値が変わってしまうため、精度の低下につながってしまいます。他にも、モデルを複数のGPUに分割する分散学習を行うという手法もありますが、分散学習ではGPU間の通信が必要で、通信も含めた学習全体で効率を出すためにはしばしば大変なチューニングを要します。
そこでニューラルネットワークの出力を変えずにメモリを削減する手法として、再計算が挙げられます。通常、計算の過程で最もメモリ消費が大きくなるタイミングでは、メモリ上に多くの一時変数が保持されていますが、これらの中には値が長時間参照されないままメモリ上に保持され続けるような一時変数も数多くあります。再計算では、後に参照される一時変数であってもメモリから解放し、必要になったタイミングでその入力をたどって再び計算してやることにより、ピーク時のメモリ使用量を下げることができます。この再計算の性質により、再計算を行ったとしてもモデルの出力は元と同一で、精度の低下を招くことはありません。その一方で計算回数自体は増えるため、むやみに再計算してしまうと実行時間の増加につながります。(1)
どのタイミングでどの変数をメモリから解放し、いつ再計算するかは最終的な消費メモリや実行時間に大きく影響し、これらを最適化することは計算量理論的にも難しい問題として知られています [link]。
ニューラルネットワークの学習に向けた再計算アルゴリズムは Chenのアルゴリズム から始まり、 Checkmate や 最近では Moccasin などの手法が知られていますが、これらは決まった形のニューラルネットワークを対象としていたり、数百ノード程度までの小さな計算グラフで動作するものでした。
PFNでは、たとえば Matlantis で用いられるネットワークなどより複雑で大規模なモデルにも対応するため、一般の計算グラフで性能のよい再計算スケジューラの開発にこれまでも取り組んでいました。
今回のインターンシップでは、さらに性能の良い再計算スケジューラの開発に取り組み、そして性能改善に成功しました。以降では具体的な再計算アルゴリズムについて話をしていきます。
(1): MN-Coreでは、問題設定は異なりますが、再計算により実行時間を短くするといった面白い最適化がなされています。興味のある方は https://tech.preferred.jp/ja/blog/mncore-compiler-optimization-with-recompute/ をご覧ください。
計算グラフの定義
本稿では各値について、その値を保持するのに必要なメモリ量や、その値を計算するのにかかる時間があらかじめ分かっていると仮定して話を進めます。
また、計算グラフの各頂点は値を表しており、どの値がどの値を計算するのに必要になるか、という依存関係を有向辺で表すことにします。
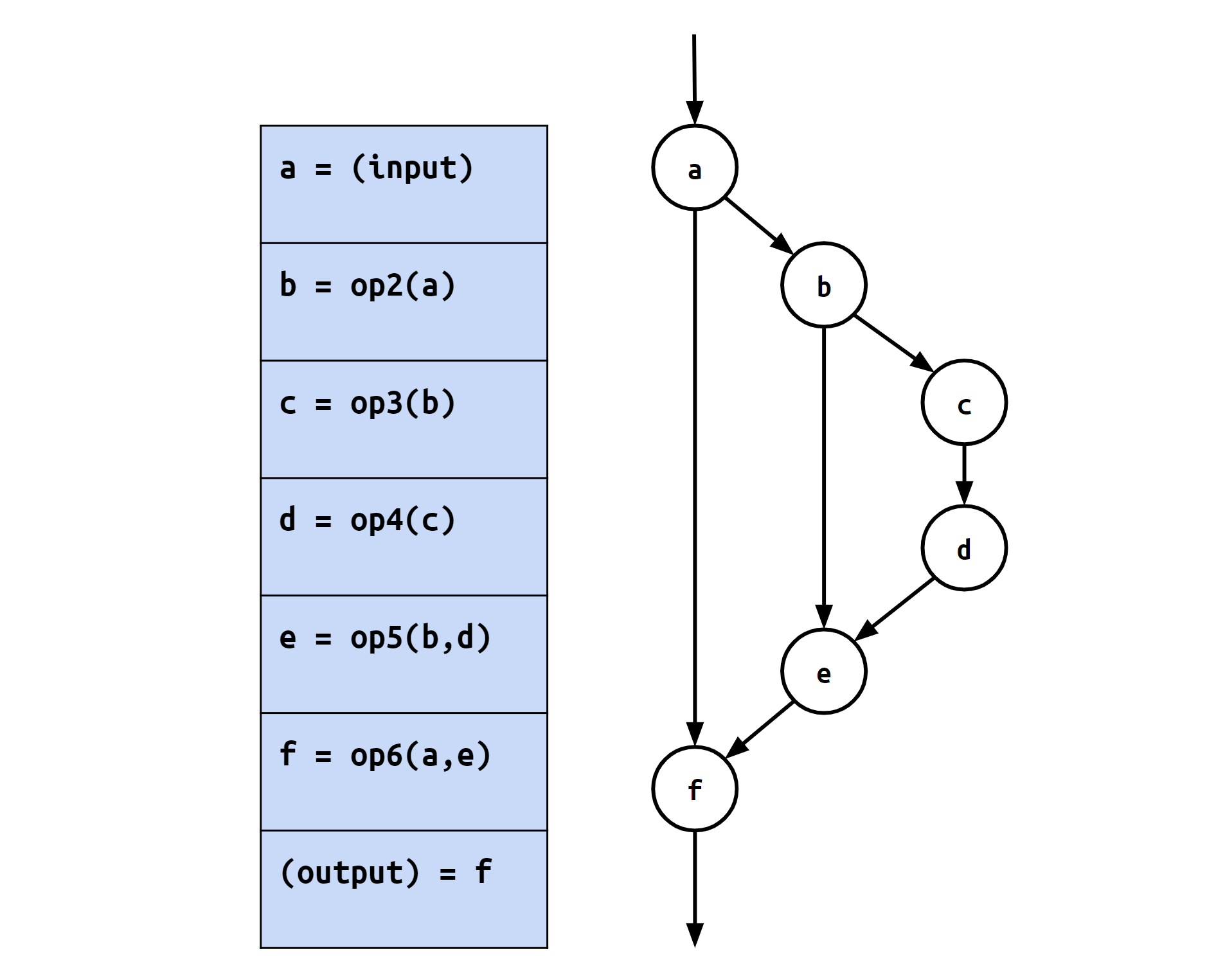
例えば上図のような計算グラフの場合、eを計算するにはbとdが必要であり、そしてeがfの計算に用いられます。
さらに、行う計算を順番に列挙したものを計算列と呼ぶことにします。上記の例では、計算列としてa→b→c→d→e→fというものが得られます。
メモリの解放とピークメモリ
計算グラフにおいて全ての計算結果を保持し続けた場合、モデルが巨大な場合には学習中のメモリ不足に繋がります。そこで以下の図のように、各計算結果について不必要になったタイミングで即座にメモリから解放するとします。
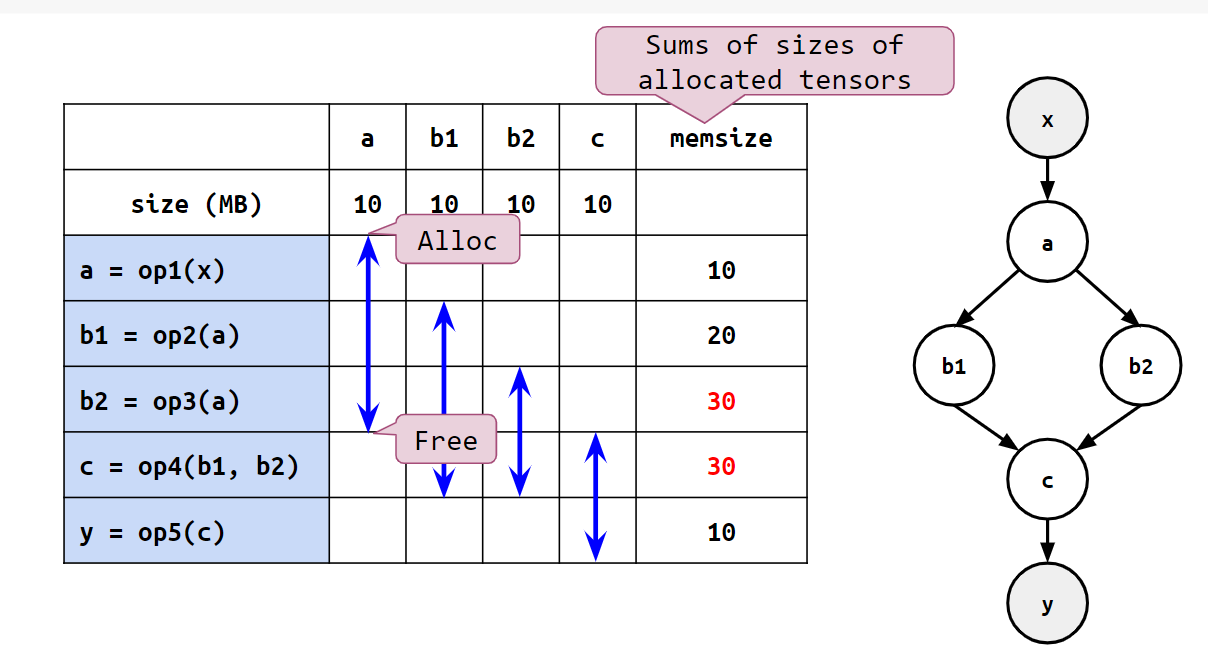
例えば、aはb1とb2を計算した後に即座に解放することで、以降の計算におけるメモリ使用量を抑えることができます。
メモリ使用量が最も大きくなるタイミングをピークと呼び、その時点でのメモリ使用量をピークメモリと呼ぶことにします。上の例ではb2やcを計算する際のメモリ使用量が最も大きく、ピークメモリは30です。
計算順序
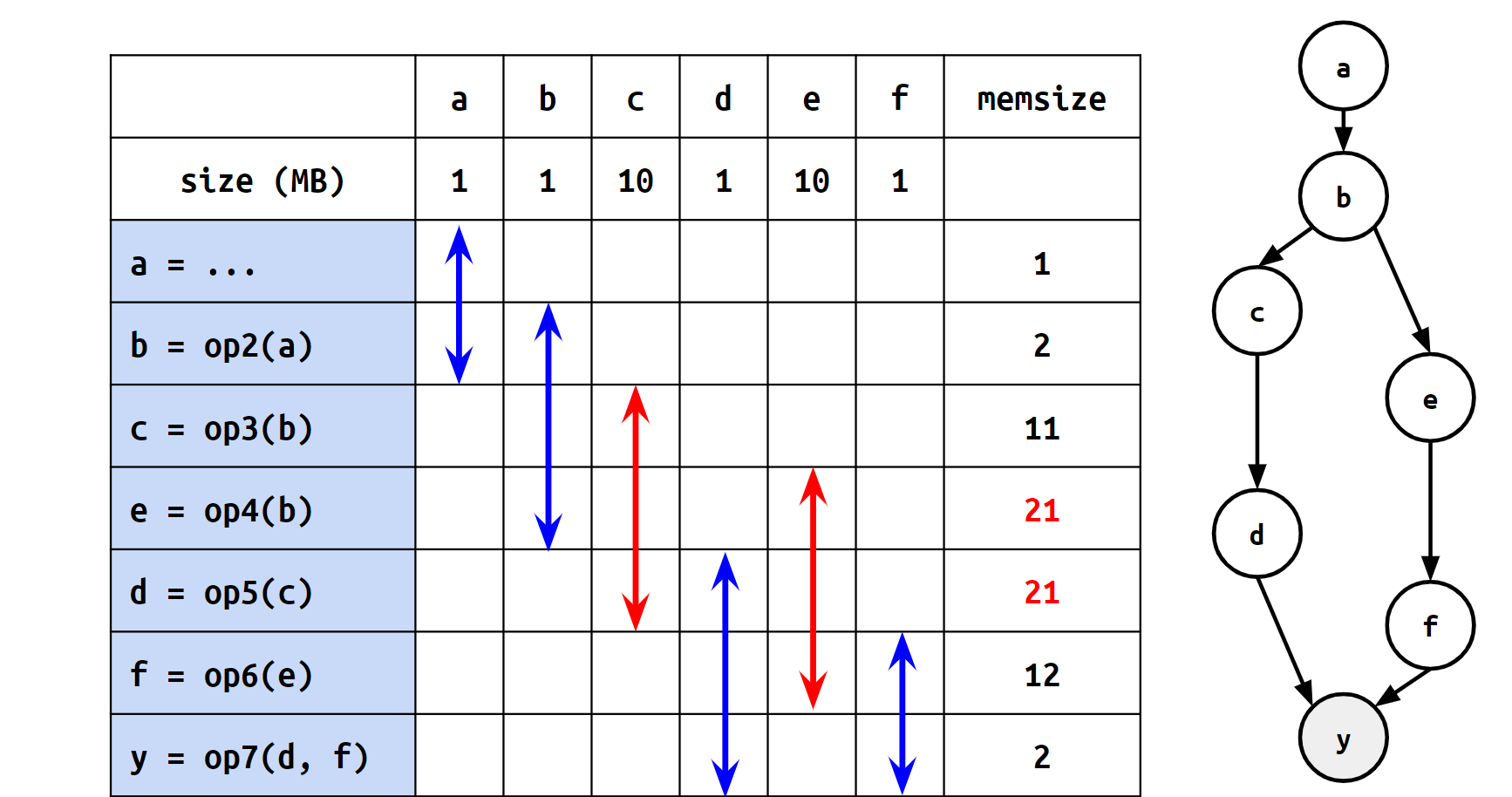
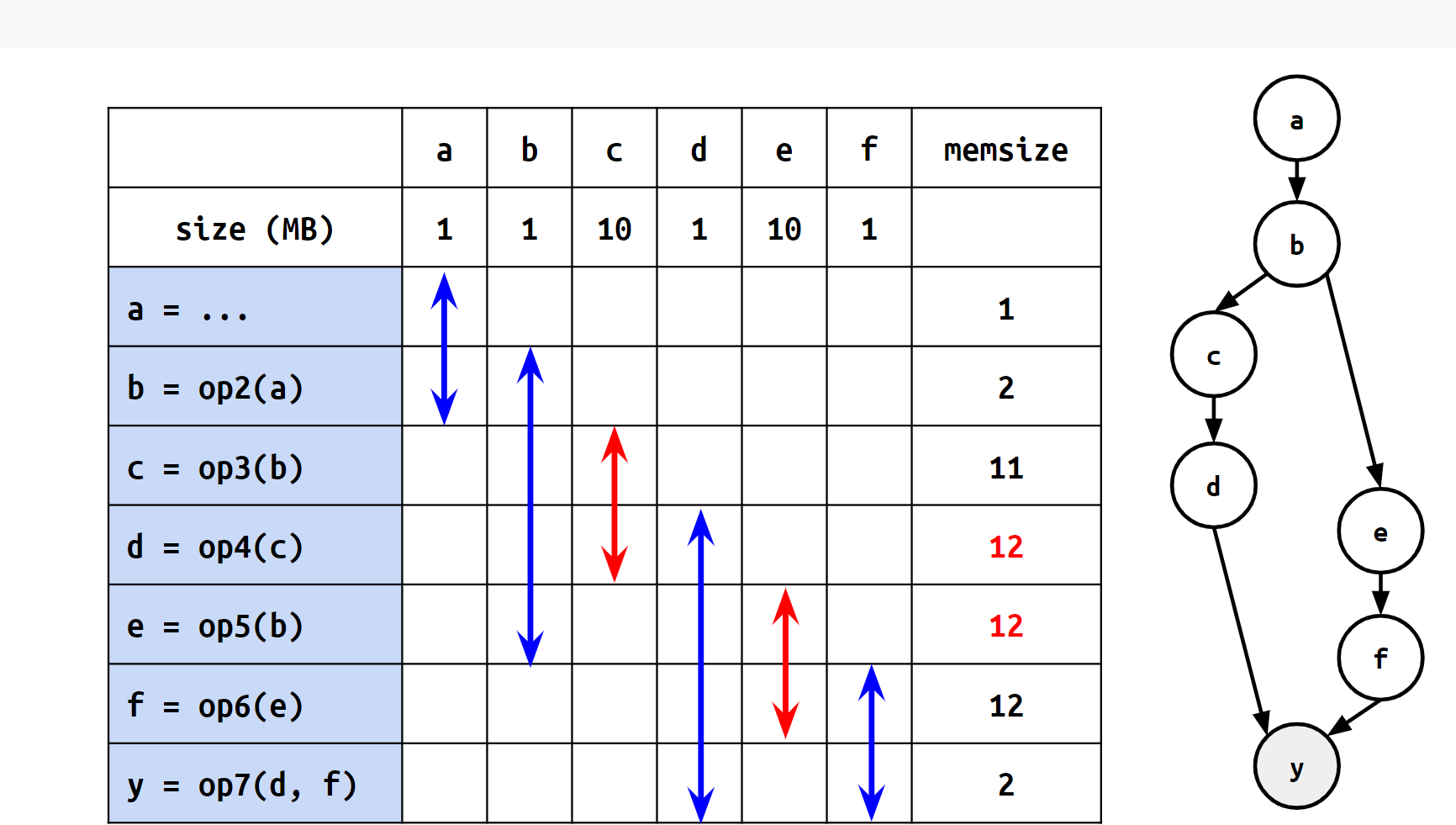
同じ計算グラフで表現される計算の列であっても、計算を行う命令の順序によってピークメモリが異なります。例えば、以下の2つの図は計算グラフ自体は同一のものですが、計算順序の違いによってピークメモリに差が出ています。
再計算
前項で述べた通り、各値は自身を入力としてとる計算が全て終わるまでの間はメモリに保持され続けることになりますが、値によっては長時間入力として参照されないままメモリに保持され続けることもあり、その間のメモリ使用量が増加してしまいます。
そこで、自身を入力としてとる計算がまだ残っていたとしても一度メモリから解放してしまい、必要になった時にまた計算しなおすことでこの長時間の間のメモリ使用量を抑えることができ、結果としてピークメモリを抑えられることがあります。これを再計算と言います。
例えば、以下の図を見てみます:
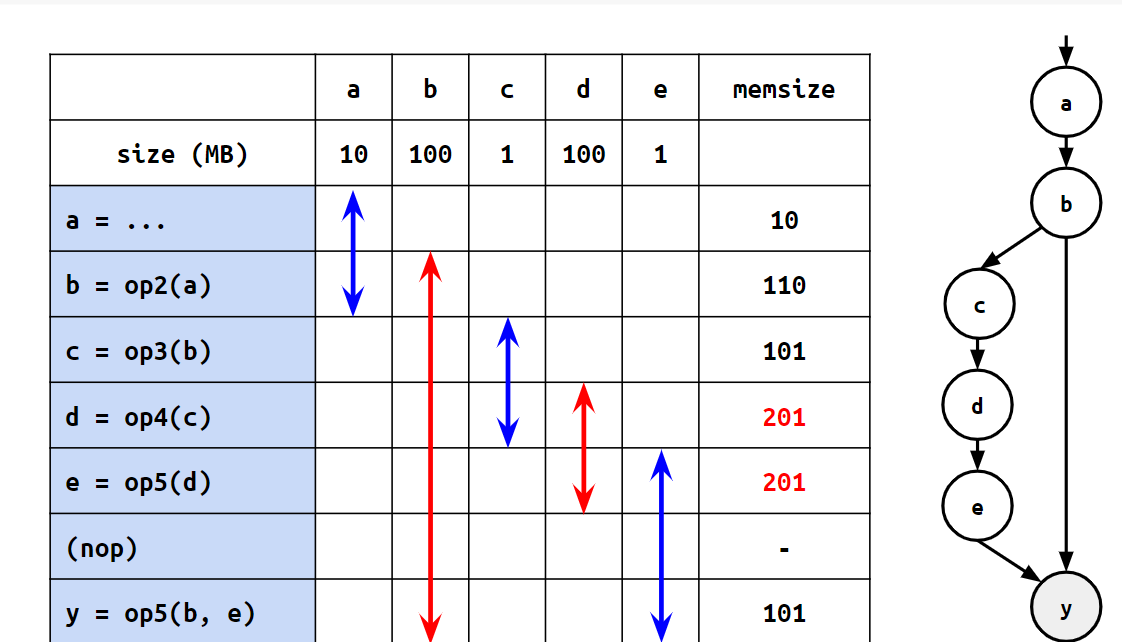
この時、bはyの計算に必要なので、dやeを計算する間も覚えておく必要があります。そこで、以下の図のように、bをyの直前に再計算することにしてみます。
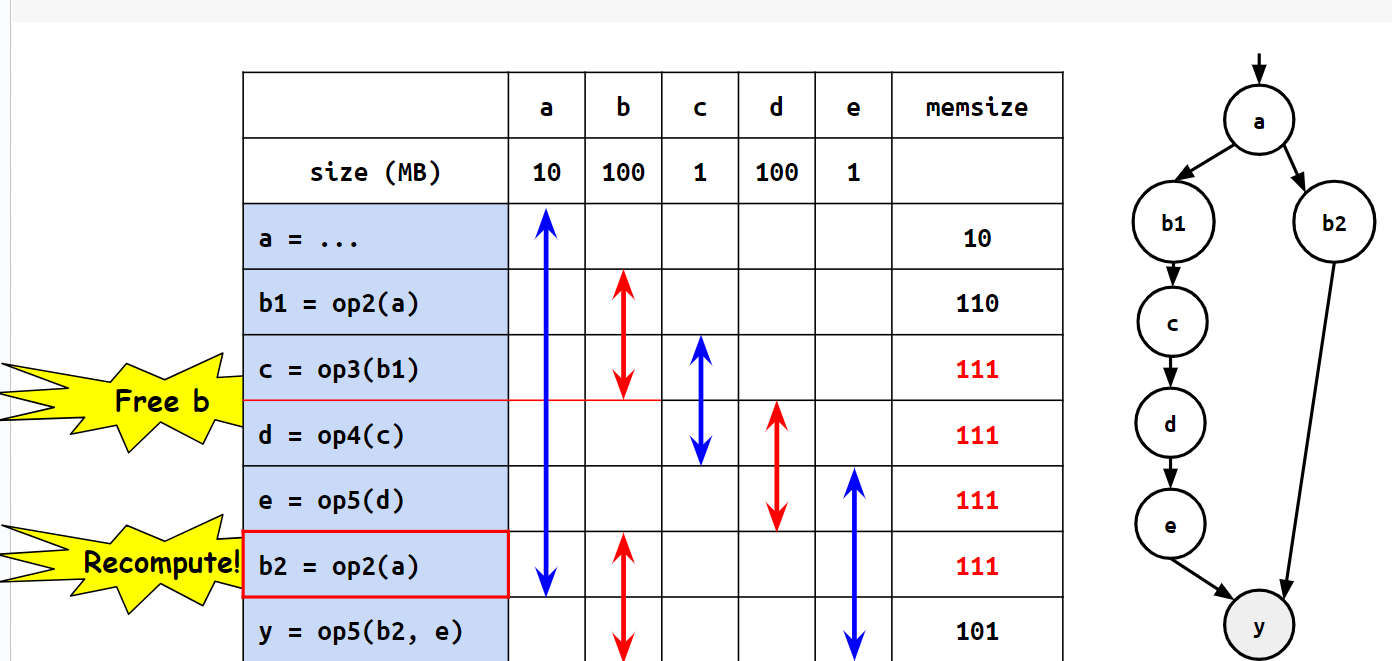
こうした場合、dやeを計算している間はbをメモリから解放できるため、ピークメモリを抑えることができるようになります。その代わり、bは2度計算しているため、実行時間自体は長くなっています。(2)
このように、どのような計算順序が良いのか、あるいはどのタイミングでどの値を再計算すれば良いのか、という戦略をうまく組み立てることで、できるだけ少ないオーバーヘッドで適切にピークメモリを抑えられる計算列を得よう、というのが再計算アルゴリズムの目的になります。
より詳しい内容についてはこちらのblogで説明されています。
https://tech.preferred.jp/ja/blog/recomputation/
(2): b1,b2はともにbのことを表しています。便宜上このように数字付けで表現しています。
再計算アルゴリズム: FastSA について
再計算をうまく行うアルゴリズムとして、PFNが提案したFastSAという再計算アルゴリズムを紹介します。
以下、便宜上計算グラフの頂点数を\(V\)、辺数を\(E\)とします。また、各計算nodeのことを単純にnodeと呼ぶことにします。まず、最適な計算列を求めるにあたって、焼きなまし法(Simulated Annealing)という手法を用います。焼きなまし法の近傍遷移として、
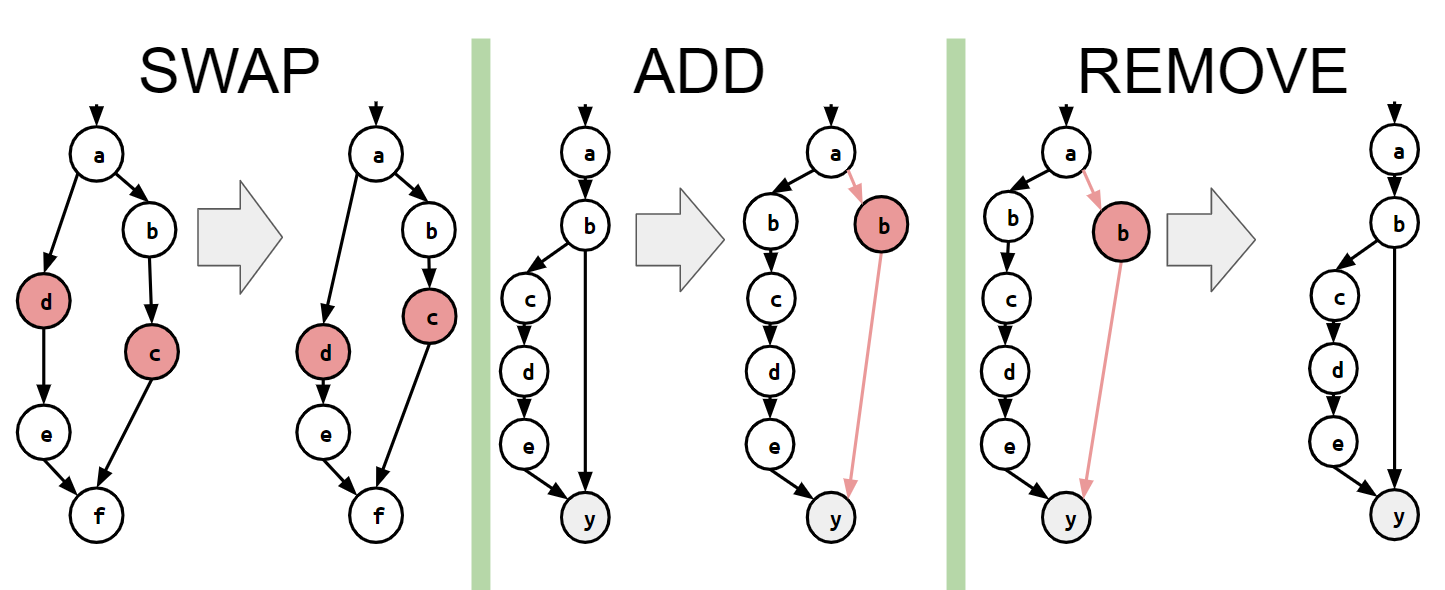
- nodeを1つ選び、このnodeを別のタイミングと入れ替える(SWAP)。
- nodeを1つ選び、このnodeを別のタイミングにも追加する(ADD)。
- nodeを1つ選び、削除する(REMOVE)。
という3種類の遷移が考えられます(下図参照)。
近傍遷移において、遷移後のピークメモリを毎回1から計算し直すことにすると、焼きなましを繰り返す回数を\(T\)として時間計算量が\(O((V+E)T)\)になります。
しかし、巨大な学習モデルではVやEが5000から10000ほどになることがあり、そのような場合には焼きなまし法が収束するまでかなり長い時間が必要になる、という問題がありました。そこでこの焼きなまし法の近傍遷移に対して、Segment Treeと呼ばれるデータ構造を用いることで、遷移後のピークメモリをグラフの大きさに対しておよそ対数時間で求められるようになる、というのがFastSAで提案されている手法の主要な部分です。
より詳しい内容についてはこちらの論文(NeurIPS2023で発表予定)をご覧ください。
https://openreview.net/forum?id=fbpTObq6TW
課題
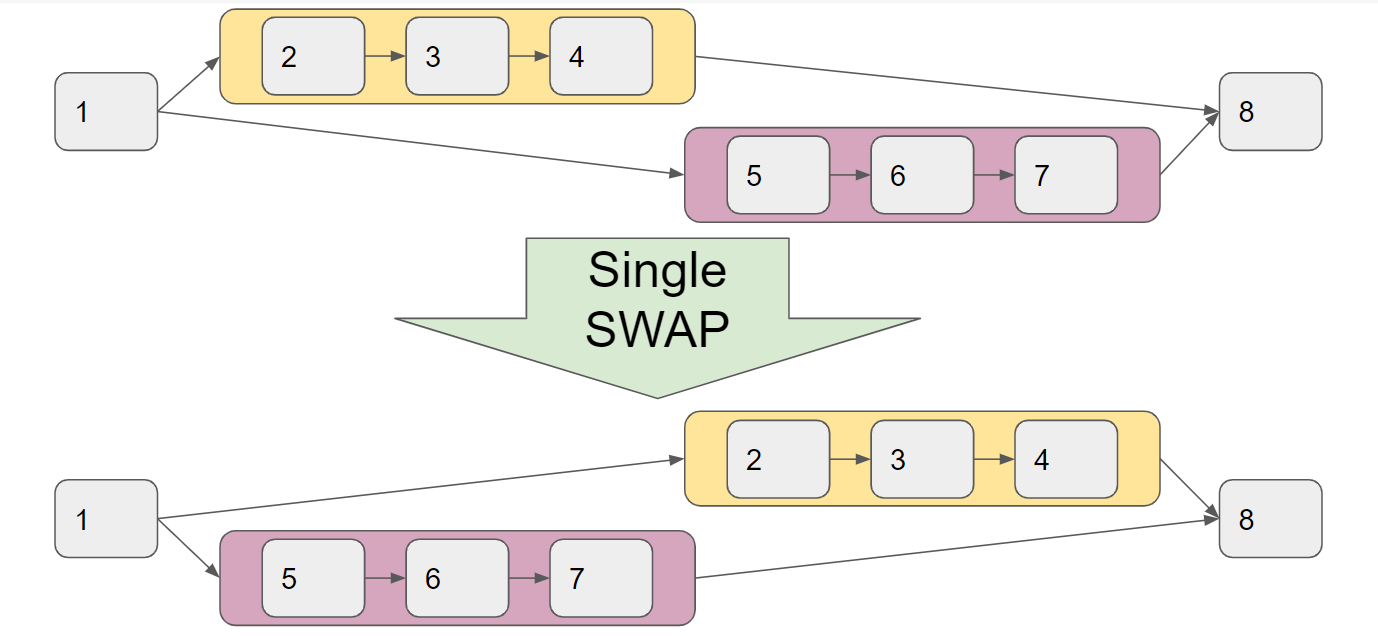
焼きなまし法では、以下の図のように、複数のnodeからなるnode sequence(2-3-4や5-6-7)の計算順序が丸ごと入れ替わったような状態にたどり着くのはかなり難しいです。
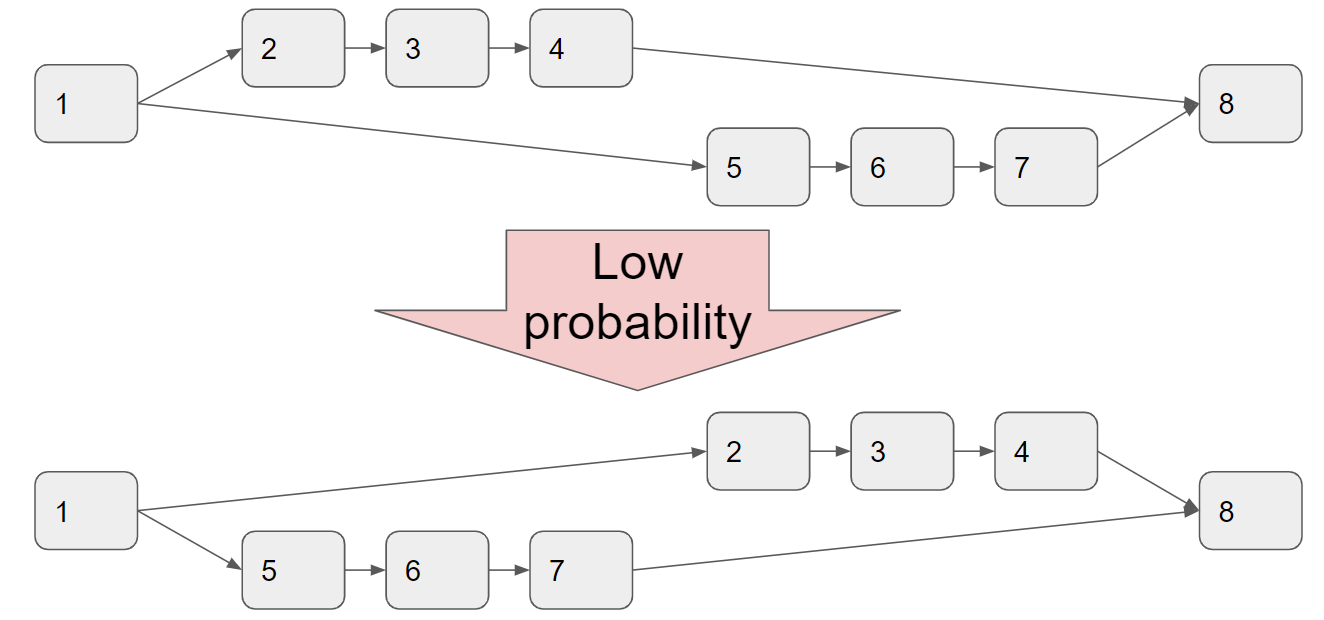
FastSAでもこの課題には触れられており、順番に計算していくしかないようなnode(上図では2-3-4や5-6-7の部分)を1つの大きなnodeとしてあらかじめGroupingしておき(下図参照)、このGroupingされたnodeのみからなる計算グラフで焼きなまし法を適用するという手法がとられています。
今回のインターンシップでは、このnodeをgroupingする手法をより一般化したgraph contraction preprocessingをうまく導入し、この課題に対するより良い改善策を模索するのが主な課題となりました。
アプローチ
Graph contraction preprocessing
以下の図のように、いくつかのnodeをmarkし、このnodeのみからなる縮約されたグラフにすることを考えます。イメージとしては、markされたnodeが、groupingされたnodeの末尾となるように縮約しています。
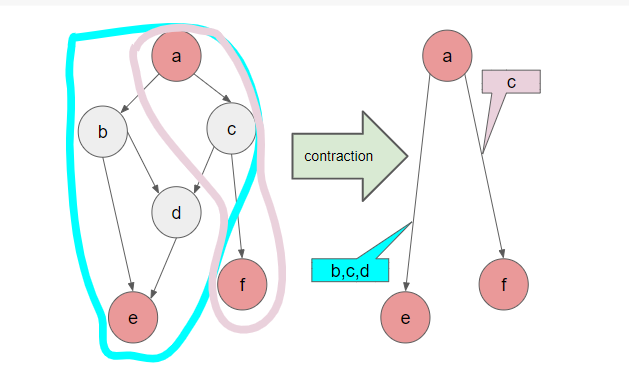
例えばこの図では、a~fの6つのnodeが{a,e,f}からなる3つのnodeに縮約されていますが、eは実際には{b,c,d,e}というnode groupを表しており、aからeを計算する際にはa→b/c→c/b→d→eの順番で計算します。同様にfは{c,f}というnode groupを表しており、aからfを計算する際にはa→c→fと計算します。(3)
上図のeをaから計算する際にb,cのどちらを先に計算するかの2通りの方法があったように、markしたnodeからmarkしたnodeを計算する間の計算列も最適な順序を考えるとより良い縮約ができます。これはすなわち、inputがa、nodeが{b,c,d,e}、outputがeであるようなsubgraphで同じ問題を解くことになります。そこで、node数が少ない場合の最適な順序について考察することにします。ピークメモリとオーバーヘッドの両方を考慮するのは難しいため、ここではピークメモリの最小化を考えることにします。(4)
(3): この縮約を行った時点で、cはeを計算する際とfを計算する際の2度計算されることになります。このようにmarkされていないnodeは再計算されやすいため、必要メモリ量が大きいnodeほどmarkされないように、markするnodeを選んでいます。
(4): ピークメモリの最小化を考えることにした背景には、焼きなまし法はピークメモリが減少する遷移は行いにくいが計算時間のオーバーヘッドを抑えるような遷移は行いやすいということが経験上分かっている、というものがあります。
Optimal computational sequence in subgraph
まず、グラフ内の各nodeについて、このnodeが現在メモリで保持されているか保持されていないかの2通りの状態が考えられるため、計算の過程であり得る状態の個数は \(2^V\) 個と考えられます。
さらに、各状態について、次の2種類からなる\(O(V)\)通りの遷移が考えられます。
- メモリで保持されていないnodeを1つ選び、今の状態から計算できるなら計算する
- メモリで保持されているnodeを1つ選び、このnodeをメモリから解放する
具体的には、以下の図のようにb,e,fがメモリに保持されている場合では、5通りの遷移が考えられます。
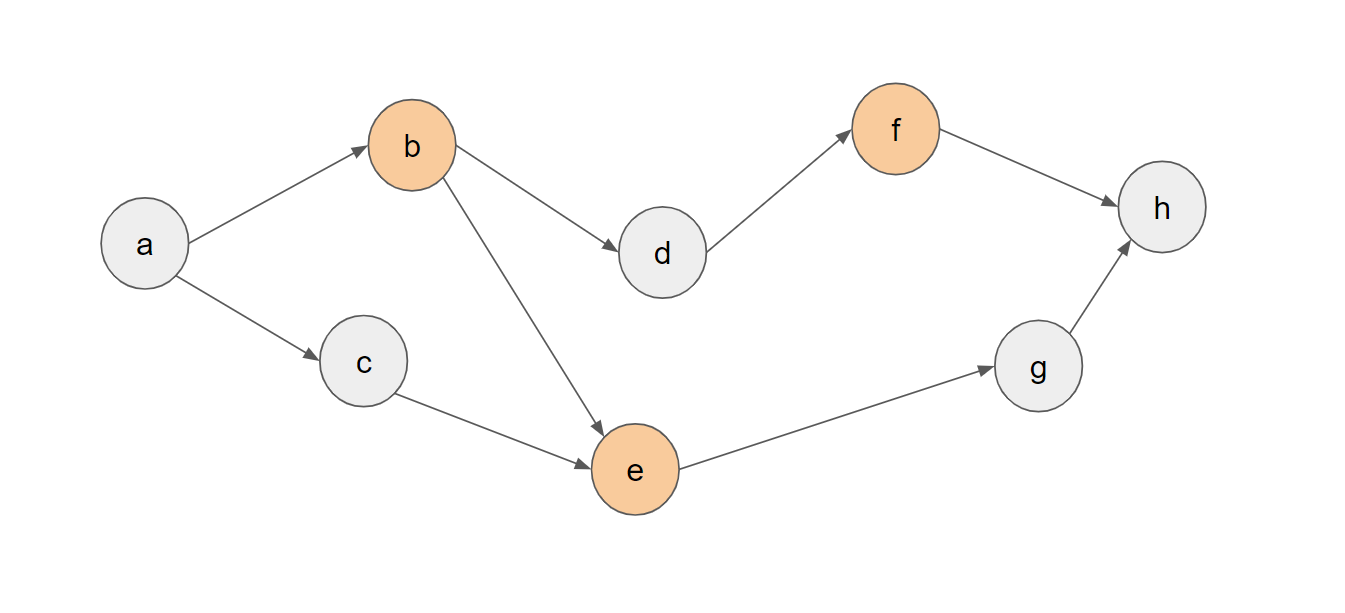
- bからdを計算し、{b,d,e,f}がメモリで保持されている状態にする
- eからgを計算し、{b,e,f,g}がメモリで保持されている状態にする
- bをメモリから解放し、{e,f}がメモリで保持されている状態にする
- eをメモリから解放し、{b,f}がメモリで保持されている状態にする
- fをメモリから解放し、{b,e}がメモリで保持されている状態にする
したがってdijkstra法を適用することで、時間計算量\(O(V^2 2^V)\)、空間計算量\(O(2^V)\)で最適な計算順序によるピークメモリを求めることができます。このdijkstra法では状態{a}から始まり、状態{h}に到達することが目標になります。
経験上このdijkstra法では\(2^V\)個の状態のうち十分多くの状態を経由しなければ目的の状態に到達できないため、\(V \leq 20\)ぐらいでないと十分高速には動きません。そこで、計算順序をそのまま前から見るのをやめて、後ろから見ることにします。この時は、「次に何を計算するか」ではなく、「最後にどのnodeを計算したのか」が遷移のキーワードとなり、以下のように遷移することになります。
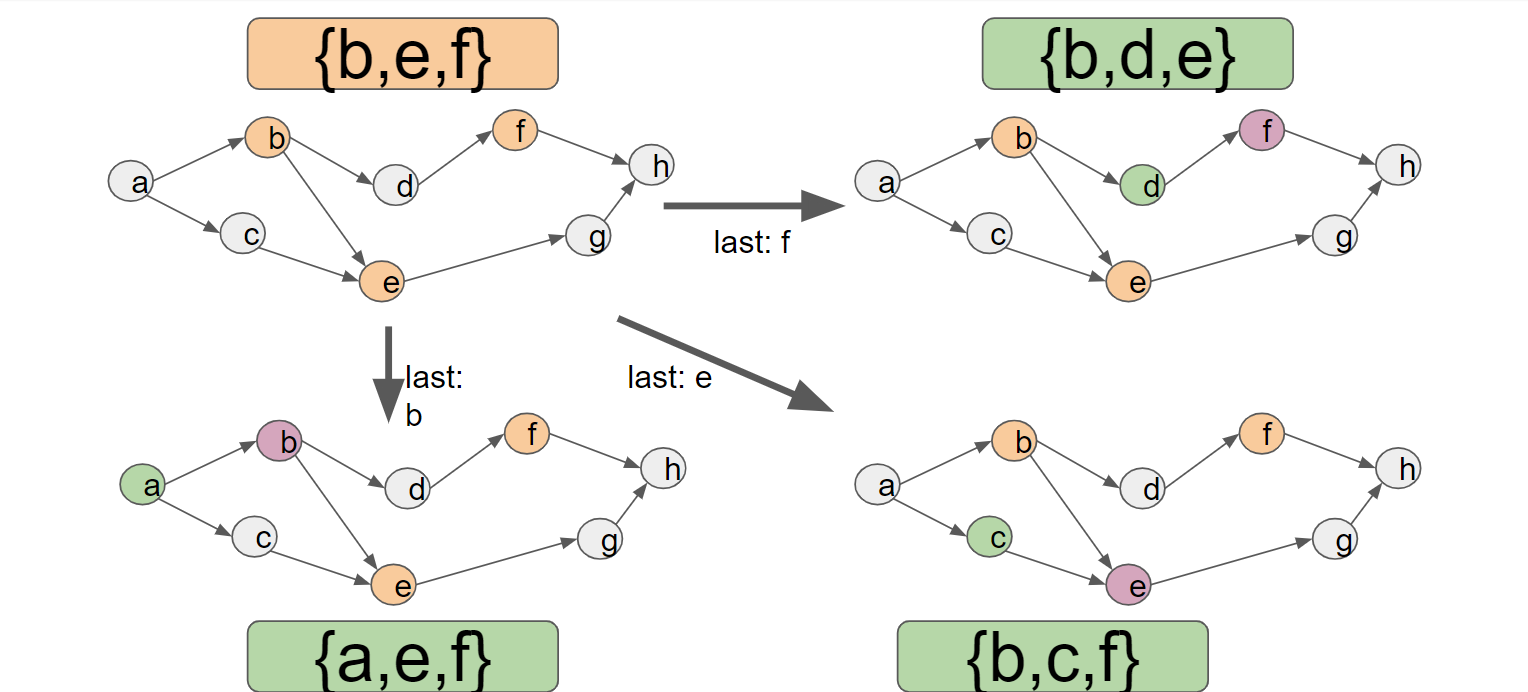
この時、dijkstra法は{h}の状態から始まり、最終的に{a}を求めるのが目標になります。
更に、前から見る場合とは異なり、後ろから見た場合は次のような枝刈りができます。以下のような状況を考えます:(5)
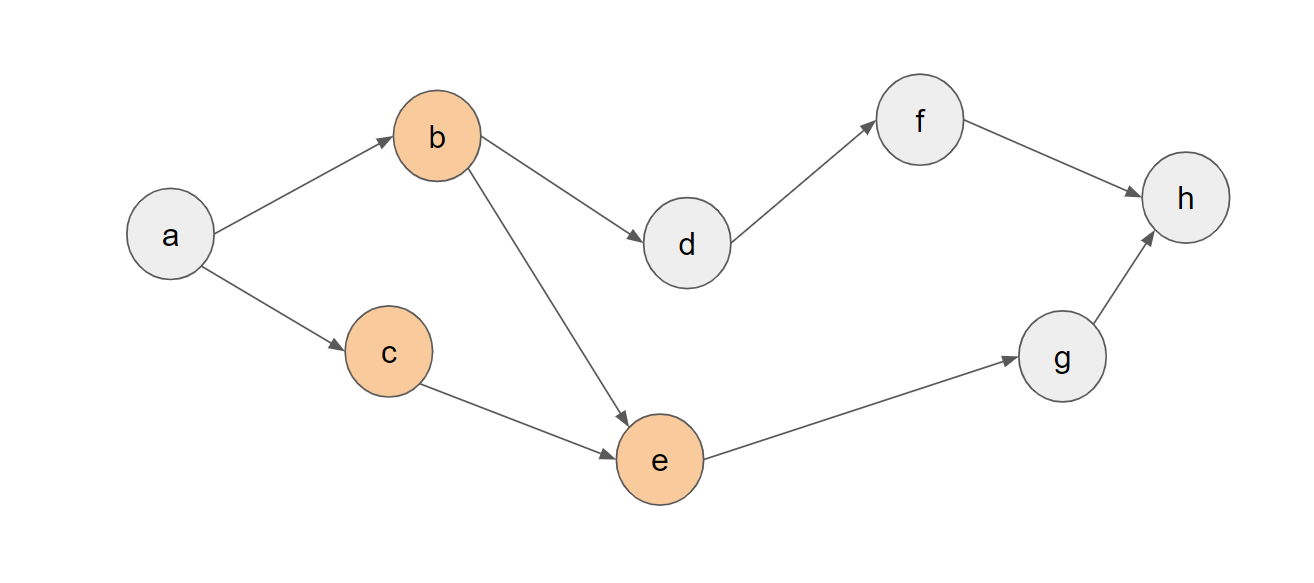
この時、以下の3通りの遷移が考えられます:
- bをメモリから解放し、{a,c,e}がメモリで保持されている状態にする
- cをメモリから解放し、{a,b,e}がメモリで保持されている状態にする
- eをメモリから解放し、{b,c}がメモリで保持されている状態にする
ここで、{b,c,e}→{b,c}の遷移は明らかに損の無い遷移となっているので、この遷移のみを行うことにします。
この枝刈りを適用すると、依然として最悪時間計算量は \(O(V^2 2^V)\) であるにも関わらず、なんと実データ上では \(V \leq 50\) ぐらいまでなら高速に動くことが判明しました。これはすなわち、50個程度のnodeを1つのまとまったnodeに縮約できるということを意味しており、焼きなましでより大きな遷移が実現できるようになりました。
また、この枝刈りを利用して、以下の図のようにdijkstra法の計算回数をあまり増やさずにより多くのnodeをまとめることもできます。
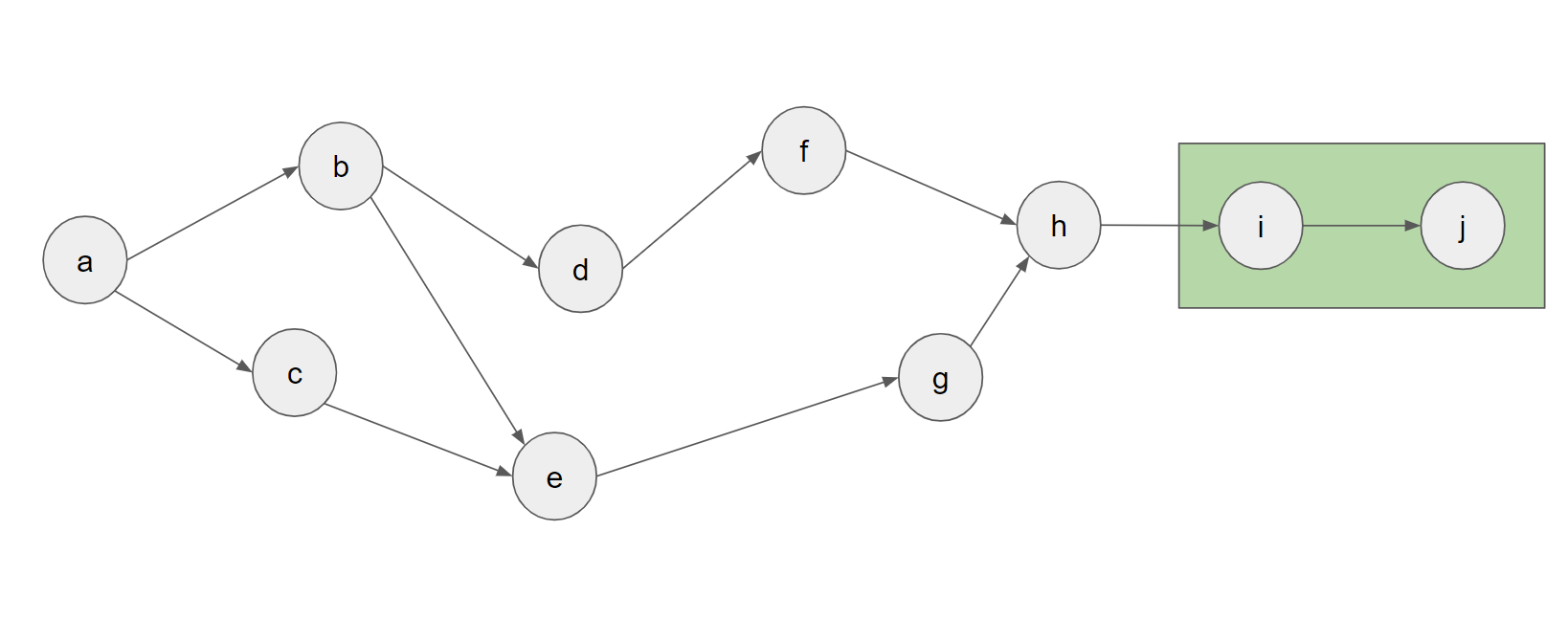
この図では、末尾にiとjというnodeが増えていますが、dijkstra法ではすぐに{j}→{i}→{h}という遷移をしていくため、前の図とほとんど同じ計算時間で最適な計算順序を求められることになります。
このような枝刈りとそれを利用したsubgraphの生成方法により、場合によってはV=60,70,…といったより多くのnodeをまとめられるようになりました。
(5): 前から見た場合の枝刈りとして、例えば{c,e}がメモリに乗っているならばcは即座にメモリから解放してよい、という枝刈りが考えられそうに見えますが、実はこの枝刈りが誤りとなる場合があります。
Graph decompose processing
さて、graph contraction preprocessingを行うとき、各processの全体像は以下の通りになっています。
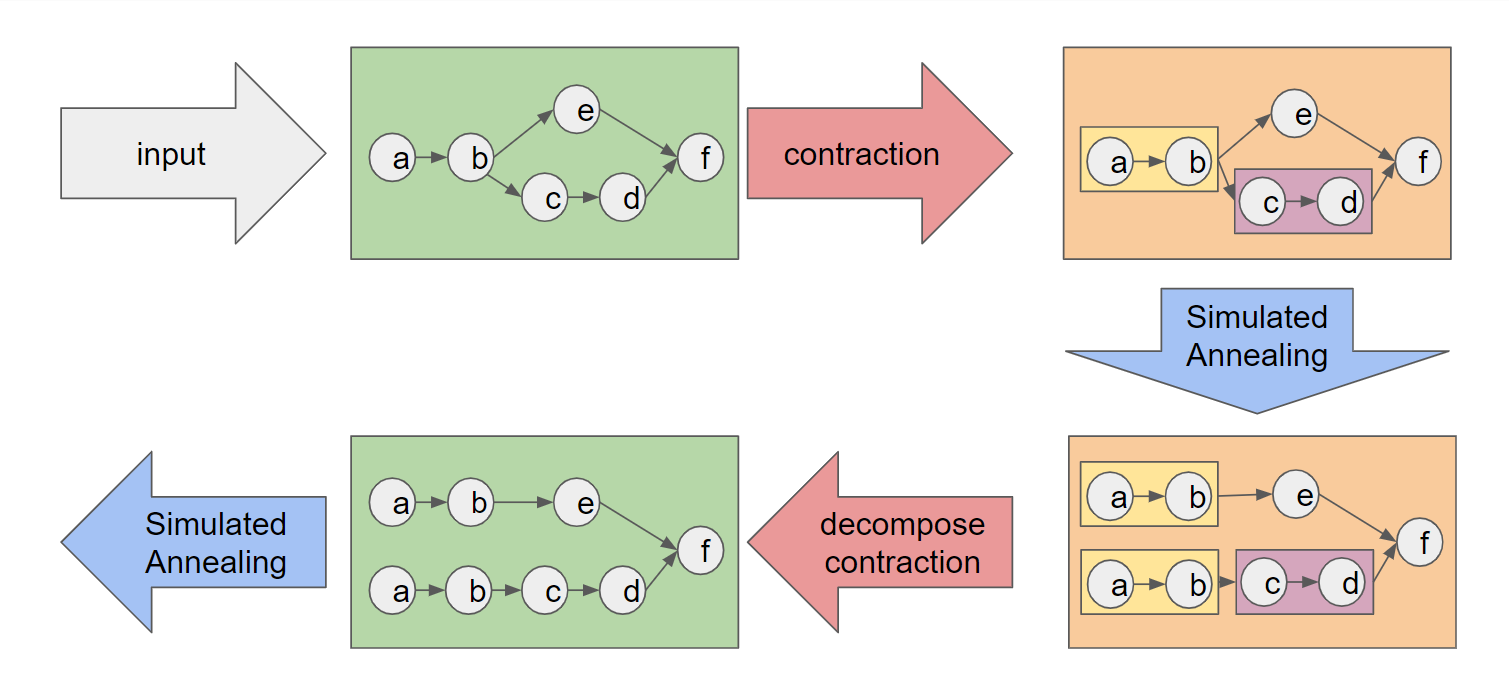
ここで、decompose contractionする際にgroupingしたnodeを一気にバラバラの元のnodeに分解していますが、50個以上のnodeがgroupingしていた場合、一気にバラバラにすると、急激な変化により焼きなまし法がうまく収束しないことがあります。
そこで、以下のようにゆっくりdecompose(6)していくと、緩やかな変化に合わせて焼きなましが遷移していき、安定して良い収束結果を得られるようになりました。
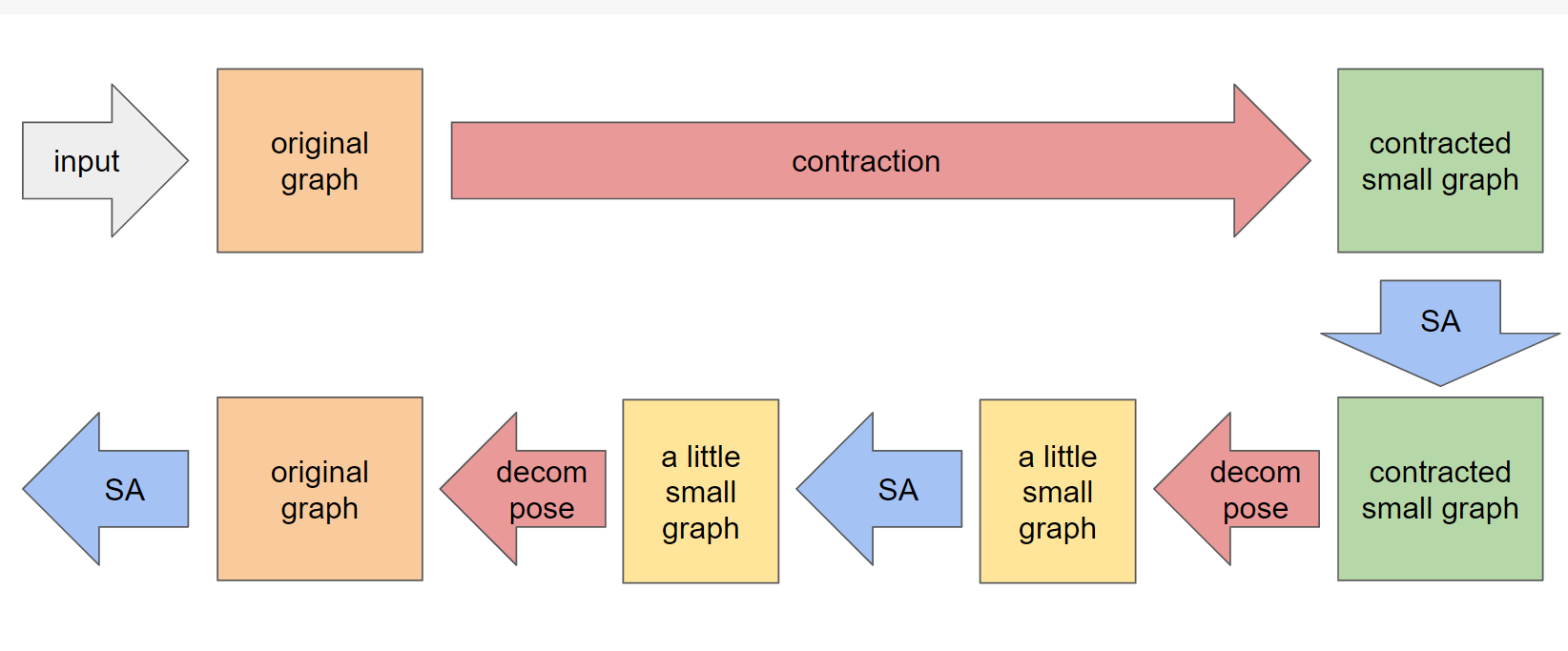
(6): 図ではdecomposeを2回しか行っていませんが、実際には何度も何度もdecomposeを行っています。
実験結果
焼きなましの評価関数として、メモリがx以下なら線形的に増加するがxを超えると指数的に増加するコスト、というものを考えると様々なメモリ削減量に対するできるだけ小さい計算グラフの総実行時間を求めることができます。
そこで、実際に様々な学習モデルに対しxの値を色々試し、アルゴリズムを適用してみました。
実験結果図では横軸をメモリ、縦軸を計算グラフの総実行時間で表しています。再計算を一切行わなかった場合の結果が(100%,100%)となるように表示しており、左側に行くほど省メモリであり、下側に行くほど高速であることを意味します。赤色の点が既存の手法であるFastSAを適用したものであり、青色の点が今回考案した手法を適用したものになります。
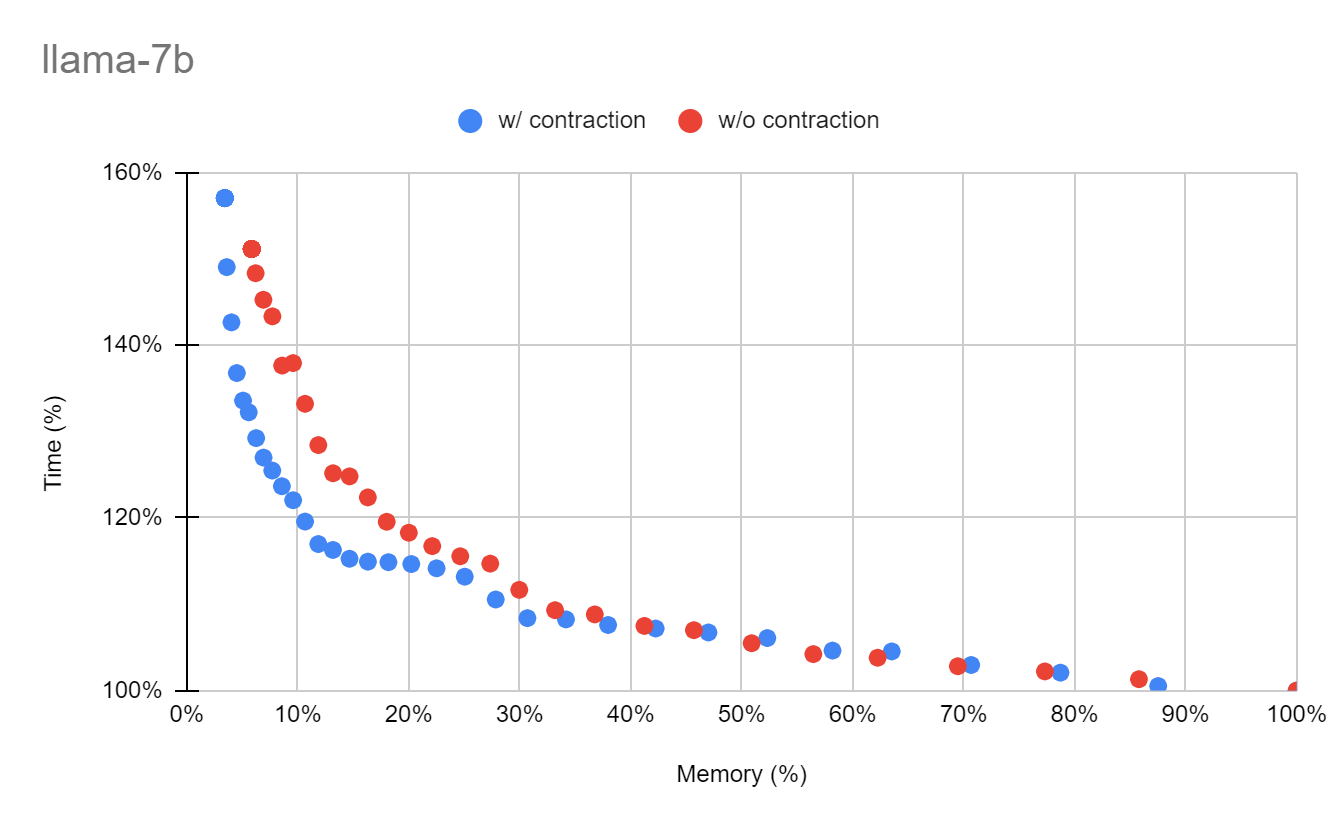
LLaMA 7B(7) モデルでは、既存の手法では5.79%までメモリを減らせていましたが、今回の手法では更に3.41%までメモリを減らすことができました。またTimeの方に着目してみると、既存の手法と比べて約140%から約120%まで大幅に減っていることが分かります。
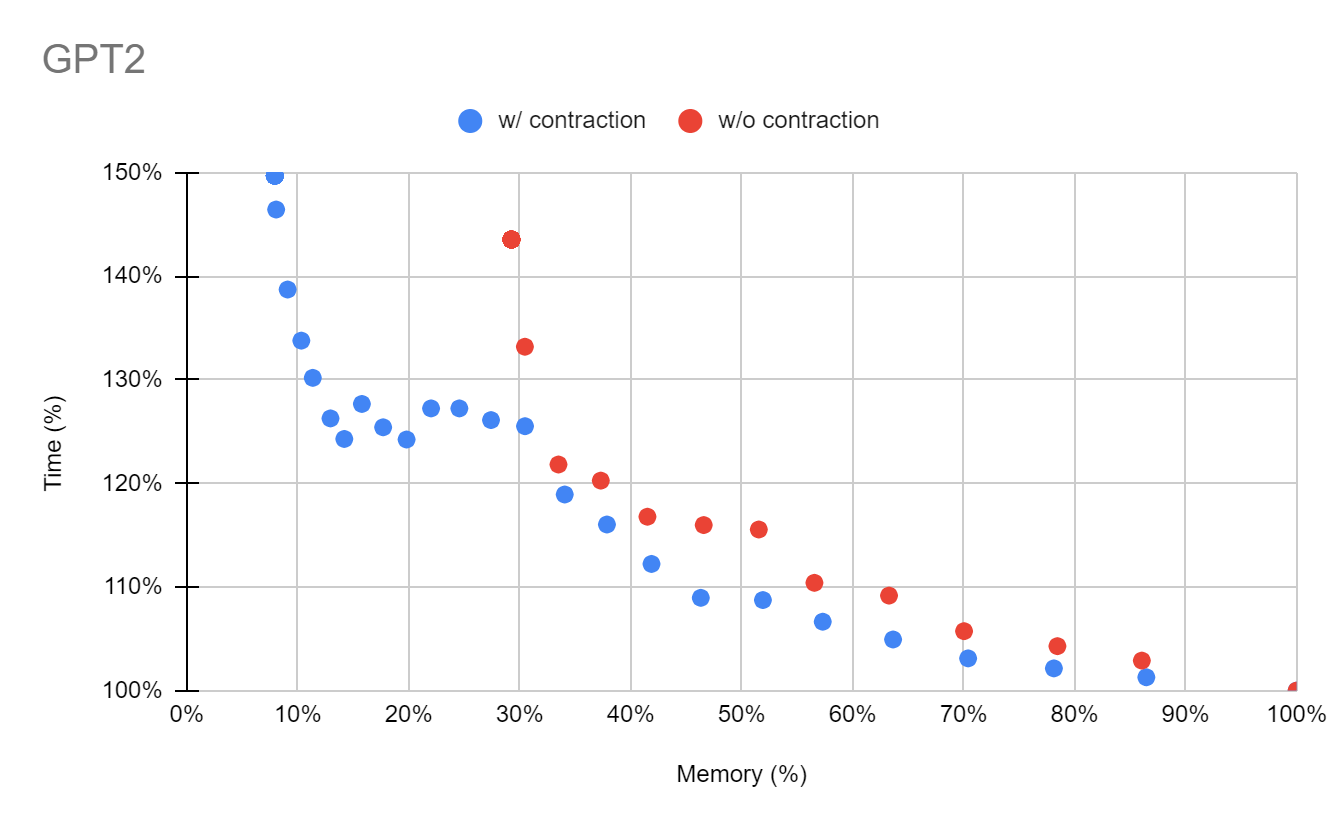
GPT-2 モデルでは、既存の手法と比べて約1/3までメモリを削減することに成功しました。既存の手法ではあまりうまくnode groupingできなかった部分をちゃんとgroupingできるようになったことが大きく影響したのだと考えられます。
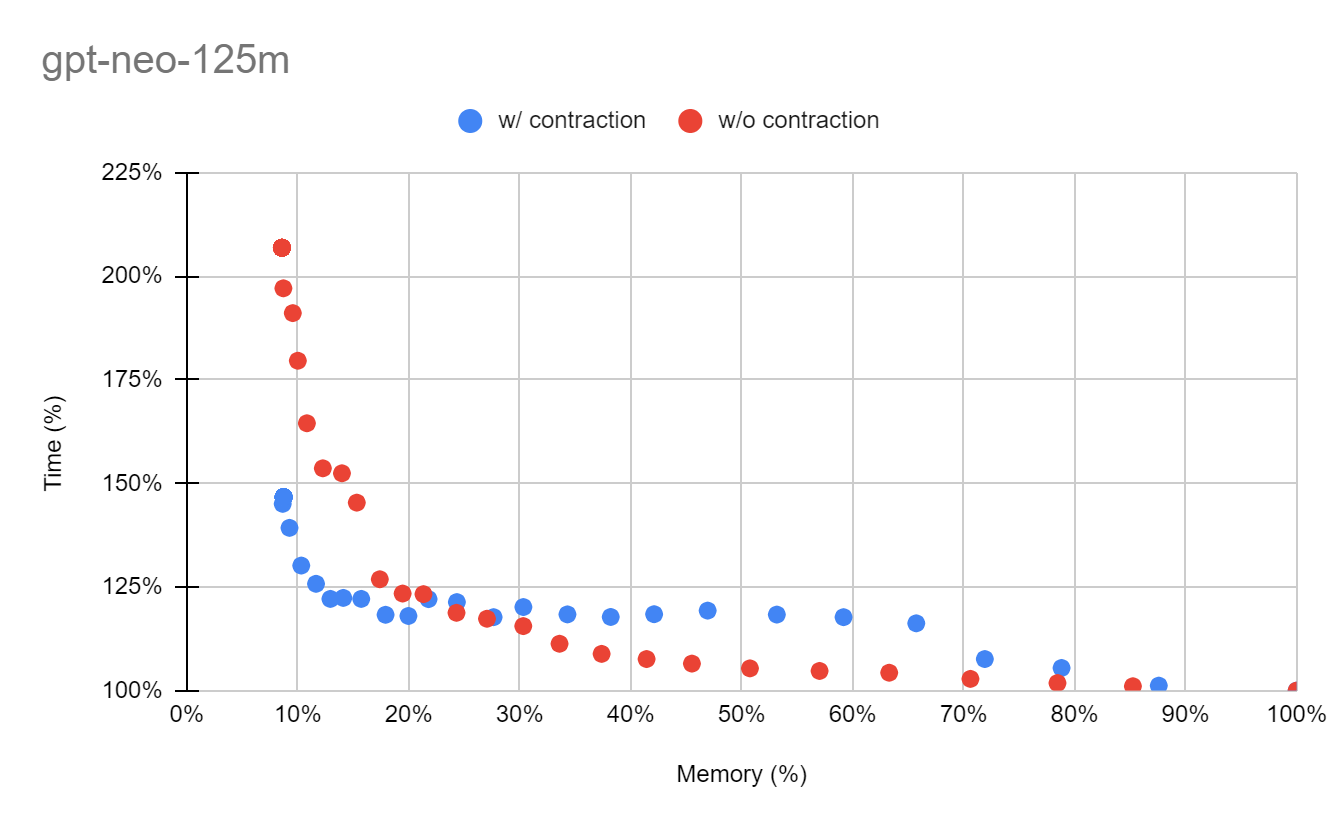
GPT-Neo-125M モデルでは、メモリを10%付近まで削減したい場合に実行時間を大きく削減することに成功しました。これはnodeをゆっくりdecomposeした結果、途中でうまく再計算ノードが削除されていったのが要因だと考えられます。
このように、インターンシップ期間中は約40種類のモデルでベンチマークをとっていましたが、ほとんどのモデルに対して大幅な性能改善に成功しました。
(7): batch_size=8, context_length=2048
まとめ
今回のインターンは、「再計算アルゴリズムの性能向上」という目標に対して、どういうことをすれば性能向上が見込めるのか?という手段を探すところから始まりました。手段を思いついて実装しても性能向上に繋がらないことは多々あり、当初はちゃんとインターン期間中に成果を出すことができるのだろうか、という不安もありました。
そんな中でメンター・副メンターの方々とアルゴリズムについて相談したり、ホワイトボードに色々なグラフを書いて考察したり、実際に色々実装してみてログを凝視して因果関係を探ったりして、性能向上に成功した瞬間はとても嬉しく、非常にやりがいのあるプロジェクトだなと感じることができました。
様々な案を思いついては実装し、性能が向上したりしなかったりを繰り返しているうちにあっという間にインターン期間の終了が来てしまいました。もっと時間があればもっと性能向上できただろうなという心残りはありますが、このような面白い挑戦に1か月半全力で取り組むことができたのは非常に良い経験になりました。




