WilcoxonPruner: 統計的検定に基づくOptunaの新しい枝刈り

王允卓

このブログは3月18日にリリースされたOptuna v3.6の新機能を紹介する最初のブログです。

Optuna v3.6には様々な新機能が含まれます。このブログでは、WilcoxonPrunerと呼ばれる新しいPrunerについてご紹介します。WilcoxonPrunerは様々な問題インスタンスに対する評価結果の平均や中央値を最適化したいという問題設定において威力を発揮するPrunerです。応用領域としては、交差検証を用いたハイパーパラメータ最適化や大規模言語モデルの精度の推論時最適化などが考えられます。

はじめに

Optunaに以前からあるPrunerは深層学習等の機械学習モデルのハイパーパラメータ最適化を想定していました。各Trialの評価（＝モデルの学習）途中で学習曲線が逐次的に得られるときに、Prunerはこの学習曲線に基づいて筋の悪いTrialの評価を早期停止します。このような問題設定では前半に性能が悪かったとしても最終的に良い結果を出すTrialの可能性を否定することが難しいため、Prunerは保守的である必要がありました。

今回導入されたWilcoxonPrunerは、前述の問題設定とは異なる応用を目的に設計されています。具体的には、ある問題を解くソルバーのパラメータを探索して、複数の設問（以降では問題インスタンス、あるいは単にインスタンスと呼びます）に対する回答スコアの平均や中央値を最適化するという問題設定です。各インスタンスに対するスコア計算ののち、WilcoxonPrunerは現在のTrialがその時点までのベストなTrialと比べて統計的によくなりそうにないかどうかを判定し、そのような場合に評価を打ち切ります。

具体的な応用領域としては以下のようなものが考えられます。

メタヒューリスティクス手法（例: 焼きなまし法・遺伝的アルゴリズム）や高度なSATソルバー等のハイパーパラメータの調整による、特定の問題ドメインにおけるパフォーマンスの最適化
機械学習モデルのハイパーパラメータのk-fold交差検証スコアの最適化
大規模言語モデル(LLM)の複数の質問に対する出力の精度の最適化

例えば、GPT-4等のLLMに与える質問が100個あり、Optunaを用いて推論時ハイパーパラメータ（例：温度）をチューニングするとしましょう。GPT-4は与えられたハイパーパラメータを用いて一つ一つの質問に順に答えていきます。WilcoxonPrunerは各質問の評価のたびに、そのTrialを枝刈りすべきかどうかを判定します。GPT-4へのクエリにはコストがかかるので、このような仕組みによって実際にクエリする質問の数を削減しコストを抑えることが可能となります。

これらの応用領域は深層学習のハイパーパラメータ最適化における枝刈りとは大きく異なるものです。各スコア計算において存在する「ノイズ」を統計的に独立だと仮定することでWilcoxonPrunerは積極的な枝刈りを実現します。

コード例

以下にWilcoxonPrunerの利用例を示します。複数インスタンスに対する評価値の平均値を最小化するというシナリオを想定した模式的なコードです。実際に動作するコードが気になる方は、チュートリアルをご覧ください。


import optuna
import numpy as np

# パラメータとインスタンス1つを引数に取り、評価値を返します。
def evaluate(param, instance):
    ...

problem_instances = ...

def objective(trial):
    # パラメータをサンプルします。
    param = trial.suggest_float("param", 0, 1)

    # パラメータのスコア評価を行います。
    results = []

    # [推奨/説明後述] 各Trialにおけるインスタンスの評価順序をシャッフルします。
    instance_ids = np.random.permutation(len(problem_instances))
    for instance_id in instance_ids:
        loss = evaluate(param, problem_instances[instance_id])
        results.append(loss)
    
        # スコアの値とともにインスタンスIDを報告してください。
        # 注意: インスタンスとその対応するIDは常に同一である必要があります。
        # 各インスタンスIDがTrialによって変わると、各インスタンスとそのスコア値
        # を対応付けることができず、枝刈りのパフォーマンスが悪化します。
        trial.report(loss, instance_id)

        if trial.should_prune():
            # TrialPrunedをraiseせず、現ステップでの目的関数の推定量を返すことが推奨されます。
            # これは枝刈りされたTrialの評価情報をOptunaに伝えるためのWorkaroundです。
            return sum(results) / len(results)

    return sum(results) / len(results)

# p_thresholdが大きいと、枝刈りが発生しやすくなります。
study = optuna.create_study(pruner=optuna.pruners.WilcoxonPruner(p_threshold=0.1))
study.optimize(objective, n_trials=100)

上記のコード例では、目的関数がパラメータのスコアを計算する際に各インスタンスをランダムな順序で評価し、同時にインスタンスのIDをスコア値とともに報告しています。trial.should_prune()がTrueを返すと評価は停止され、その時点までに評価されたスコアの平均がリターンされます。

Optunaでは通常、trial.should_prune()のif文中でraise optuna.TrialPruned()を利用しますが、今回は最終的な目的関数値(スコア値の平均)の良い推定量が各ステップにおいて利用可能であるためとと、raise optuna.TrialPruned()を利用する代わりに現状の目的関数値を返します。現在のOptunaの仕様では、TrialPrunedをraiseするとTrialの目的関数値の推定量をユーザが設定することができません。一方で目的関数値の推定量を返すことで最適化性能の向上が期待できるため、ここではあえてTrialPrunedをraiseせずに目的関数値の推定量を返します。

また、評価するインスタンスの順序が最適化性能に影響を与えてしまうので、各Trialにおいてインスタンスをシャッフルすることが推奨されます。順序固定の場合に各Trialにおいて序盤のインスタンスは毎回評価及びその結果が考慮されるため、最適化結果が序盤のインスタンスに過剰適合してしまいます。インスタンスをシャッフルすることによってそのような影響を小さくすることができます。

各trial.reportの呼び出しにおいては、対応するインスタンスのIDがスコア値とともに報告される必要があり、各インスタンスIDはStudy内で常に同一である必要があります。これはWilcoxonPrunerが内部的に評価されたスコア値とインスタンスIDの対応を保持しているからです。そうしなかった場合、パラメータによる目的値の変動よりも、難易度による変動が支配的である状況で適切な枝刈りを行うことができません。

一方で、WilcoxonPrunerでは上記の対応関係が適切に保持されていれば各インスタンスのtrial.reportの呼び出し順序がどのようなものであっても構いません。つまり、WilcoxonPrunerでは各インスタンスの結果を評価終了順に報告することができるため、複数のインスタンスを計算クラスタやマルチコアCPU等で並列に評価することが可能となります。

評価結果

ここでは巡回セールスマン問題(Traveling Salesman Problem, TSP)を題材としてWilcoxonPrunerを評価します。TPESamplerとWilcoxonPrunerを利用して簡単なTSPソルバーの焼きなましパラメータ最適化を試みます。最適化中は50回のTrialを評価し、各TrialでTSPソルバーが（最大）50インスタンス（テストケース）を解きます。次の図1に各Trialにおけるインスタンスの評価数を示します。結果を見ると、WilcoxonPrunerはインスタンスの評価回数を半分以下にすることに成功しています。実際に、50インスタンス × 50Trial = 2500回のインスタンス評価を1023回に削減しています。このような時間的コストの削減は、より大きなインスタンス集合を用いる場合やより大きなn_trialsを用いる場合により大きな恩恵をもたらすことが期待されます。

図1. チュートリアルのコード例における各Trialの評価回数。インスタンス集合は50個のTSPのテストケースを含み、我々は50個のTrialを評価しました。x軸は評価されたTrialの番号を表しており、y軸は評価されたインスタンスの個数を表しています。y軸の値が50未満の場合、そのTrialは枝刈りされたことを意味します。最終的にベストなTrialとして得られたTrialを赤で示しています。

次の図2は同じ問題設定におけるWilcoxonPrunerの枝刈りの振る舞いを表しています。図の各セルは各Trial(y軸: 評価されたTrialの番号)の各インスタンス(x軸)に対する評価結果を表しており、白色のセルはそのTrialが枝刈りによって該当のインスタンスを評価しなかったことを表します。各セルの色は、各Trialにおいてサンプルされたパラメータの各インスタンスにおけるTSPソルバーの評価スコアを表します。図には多くの白色セルがあることから、多くのTrialが早期枝刈りされていることが確認できます。その一方で、x軸方向に多くの青いセルを持つ比較的性能の良いTrialは、x軸方向に白色のセルをほとんど含まず早期に枝刈りされていないことがわかります。さらに、図をy軸方向に見てみると、赤いセルが多いインスタンスや青いセルが多いインスタンスが見られます。これは各インスタンスの難易度が一様でないことを示しています。問題の難易度が一様でない場合は一般的に枝刈りが難しくなると考えられますが、各インスタンスの評価結果をTrialごとに比較することで、WilcoxonPrunerは問題の難易度の非一様性の影響を最小限に抑えているということが図2からわかります。

図2. あるStudyにおいて得られた評価スコア(TSPを解いて得られた最短距離)の可視化。x軸はインスタンスのIDを表し、y軸は評価されたTrialの番号を表します。各セルの色は、各Trialにおいてサンプルされたパラメータの各インスタンスにおけるTSPソルバーの評価スコアを表します。良い評価スコアほど各セルの色は青が強くなります。また、白色のセルは枝刈りによってそのインスタンスが評価されなかったことを表します。

次の図3は同様の問題設定において、WilcoxonPrunerの利用有無での最適化性能比較を行っています。実験ではWilcoxonPrunerの引数p_thresholdとして0.1もしくは0.01を用いました。x軸はインスタンス評価回数の累積値であり、y軸はその時点にまで見つかった目的関数値(スコア値)のベストな値を表します。WilcoxonPrunerのp_threshold=0.1の時の結果を見ると、枝刈りを行わなかった場合（No Pruner）と比較して半分程度のインスタンス評価回数で同程度のベストな目的関数値を達成しています。前述した通り、時間的コスト削減効果は、より多くのインスタンスやTrial数を用いる場合に大きくなることが期待されます。

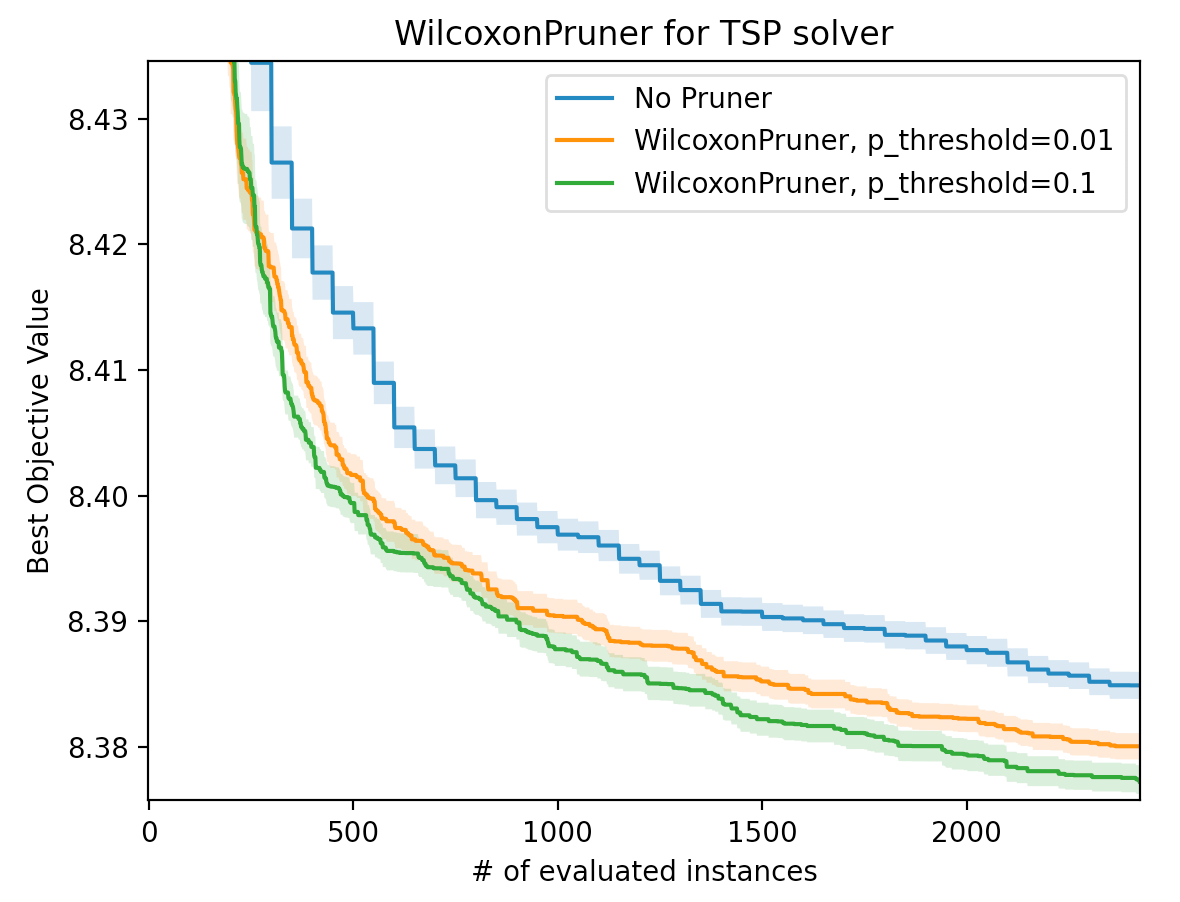
図3. WilcoxonPrunerと枝刈りなし（No Pruner）での最適化性能比較。WilcoxonPrunerはp_thresholdとして0.1もしくは0.01を用いています。x軸はインスタンス評価回数の累積値、y軸はその時点までに見つかったベストな目的関数値です。実験においてはデフォルトのSamplerであるTPESamplerを用いました。No Prunerは各Trialで50個のインスタンスを評価しました。実線は100回の異なる乱数seedに対する最適化結果の平均値であり、薄い色の帯は標準誤差を表します。

理論的背景

WilcoxonPrunerはtrial.should_prune()の呼び出しの度に、現在のTrialと現在のベストTrialで共通して評価されたインスタンスに対して、Wilcoxonの符合順位検定を内部的に行います。帰無仮説が「現在のTrialが現在のベストTrialと同程度に良い」であるとし、その片側p値がp_threshold未満である場合にWilcoxonPrunerは枝刈りを実行します。

各trial.should_prune()の呼び出しにおいて、現在の対象としているTrialに存在する全てのインスタンス評価結果\(X_n\)と現在のベストTrialでそれに対応するインスタンス評価結果\(Y_n\)を抽出します。Wilcoxonの符合順位検定では抽出されたインスタンス評価結果の組の集合\(\{(X_n, Y_n)\}_{n=1}^{N}\)に対して以下の値を計算します。

\[T := \sum_{n=1}^{N} \mathrm{sgn}(X_n – Y_n) R_n\]

ただし、\(R_n \in \{1,2,\dots, N\}\)は集合\(\{|X_n – Y_n|\}_{n=1}^{N}\)を昇順に並べた列における\(|X_n – Y_n|\)の順位です。ただし、\(|X_n – Y_n|\)の小さい\(n\)ほど順位が良くなるものとします。この\(T\)を用いて、帰無仮説の下でのp値を計算します。

Wilcoxonの符合順位検定は分布に正規性を仮定する対応ありt検定のノンパラメトリックなバージョンとみなすことができます。Wilcoxonの符合順位検定はノンパラメトリックな手法であるため正規性の仮定できない分布であっても頑健に動作します。更に分布に正規性を仮定できる場合であっても対応ありt検定に使う標本数より5%多い標本数を用意することで対応ありt検定と同等程度の検出力を漸近的に得られることが知られています[1]。

ただし、Wilcoxonの符号順位検定は正確には平均、または中央値を直接評価するものではありません。Wilcoxonの符合順位検定の正確な帰無仮説は、「２つの確率変数\(X, Y\)に対して、その差\(X – Y\)の分布が0の周りで対称であること」です。そして、片側対立仮説は「\(X – Y\)が\(Y – X\)に比べて確率的に大きい/小さい(Stochastically larger/smaller)」です。
この枠組みにおける「悪さ」の基準がユーザの目的関数の「悪さ」と適切に対応していないとき、WilcoxonPrunerの動作が適切でなくなる場合があります。また、Wilcoxonの符号順位検定はインスタンス毎の\(X_n-Y_n\)が独立同一分布となることを仮定するため、少数のインスタンスの結果が目的関数(平均など)に対して支配的になる場合、実は良い目的関数値となる場合でも枝刈りされる可能性があります。

どのようにp_thresholdを選ぶべきか？

WilcoxonPrunerはp_thresholdと呼ばれるハイパーパラメータを持ちます。このパラメータは枝刈りのされやすさを制御しており、大きな値に設定するほど、性能の悪いTrialがより早期に枝刈りされやすくなります。

問題はp_thresholdをどのように選べば良いのかということです。理想的なp_thresholdは問題依存であるため、汎用的に最適な値というものは存在しません。一方で、p_thresholdを設定する際に知っておくと良い事項を以下に示します。

統計的な観点では、p_thresholdは検定の偽陽性率、すなわち最適なTrialを枝刈りしてしまう確率を制御します。偽陽性率をどの程度まで許容できるかを決定できれば、自動的にp_thresholdも決まります。ただし、WilcoxonPrunerはtrial.should_prune()の呼び出しのたびに統計的検定を行い、一度でもp_thresholdより低いp値が得られたら枝刈りを行うため、実際には偽陽性率が設定したp_thresholdよりも大きくなってしまいます。したがって、p_thresholdはPocock-correctionをもとにインスタンス数に応じて決定すると良いです。
多腕バンディット問題の観点では、Prunerがどの程度枝刈りを行うべきかは、新しいパラメータのサンプルによってTrialを改善できる確率に大いに依存します。極端な話、特に最適化序盤であれば後に良いTrialを得る確信がある場合、現在のTrialが現時点のベストであっても枝刈りすることに意味があります。科学実験とは違い、偽陽性が出たとしても若干の追加コストが発生するだけであるため、通常は大きなp_thresholdを用いるのが良いと考えられます。この議論を前提として、0.01, 0.05といった科学実験でよく利用されるp値よりも大きな0.1をp_thresholdのデフォルト値として設定しています。

おわりに

このブログでは、複数のインスタンスに対する平均や中央値を最適化する問題において有用となりうるWilcoxonPrunerを紹介しました。このPrunerはWilcoxonの符合順位検定に基づいており、良い結果を得るまでに必要な評価回数を効率的に削減してくれます。既に実験・分析したように、WilcoxonPrunerは多くの応用領域において実験コスト削減可能性を秘めていることがわかりました。WilcoxonPrunerは新機能であるため、よりよい利用方法に関してユーザの皆さんからアイデアがあれば共有して頂けると幸いです。

Optuna v3.6には他にも強力な機能を追加しており、今後はGPSamplerの記事を投稿予定です。

このようにOptuna開発チームでは、より多くのユーザーにより便利にOptunaをお使いいただけるよう、日々改善を続けています。一緒にOptunaを開発するパートタイムエンジニアを随時募集しています。本記事を通して、ご興味を持っていただけたという方はぜひ下記ページをご確認ください。

Software engineer (Optuna) / ソフトウェアエンジニア（Optuna） / 株式会社Preferred Networks