Blog
この記事は、グローバルインターンのXinghong Fuさんによる寄稿です。
はじめに
金融市場における予測は難しいタスクと知られています。
これまで、金融市場における予測に関して様々な研究が行われており、様々なモデルが開発されてきました。
例えば、自己回帰モデル(Box 1970)、移動平均モデル(McKenzie 1984)、グローバルな単変量モデルであるN-BEATS(Oreshkin et. al. 2020)、長期予測モデル(Nie et. al. 2022)などがあります。また、大規模言語モデル(LLM)を用いた予測(Devlin et. al. 2019、Brown et. al. 2023)も試みられています。
本稿では、Googleが発表したTimesFM(Das et. al. 2024)という、時系列予測のためのモデルに着目します。
TimesFMは、Monash(Godahewa et. al. 2021)、Darts(Herzen 2022)、ETT(Zhou 2021)などのベンチマークで最高峰の性能を達成しています。
しかし、これらのベンチマークに含まれるデータは、天気、交通、検索トレンドなど、一般的で周期的なパターンを含んでいるものが多く、そのパターンをうまく抽出することが重要となっています。
しかし、株価を含む金融データは、極めて不規則で、認識可能なパターンがほとんどなく、ノイズとシグナルの比率が非常に悪いという特徴があります。
そのため、TimesFMがこういった不規則な時系列データを正しく予測できるかどうかは不明でした。
そこで、本研究においては、TimesFMに対して、様々な金融時系列を用いたファインチューニングを行い、金融データに対してもTimesFMが有効な手法であるかを検証しました。
その結果、図1に示すように、金融市場の予測において有効なケースがあることが確認できました。
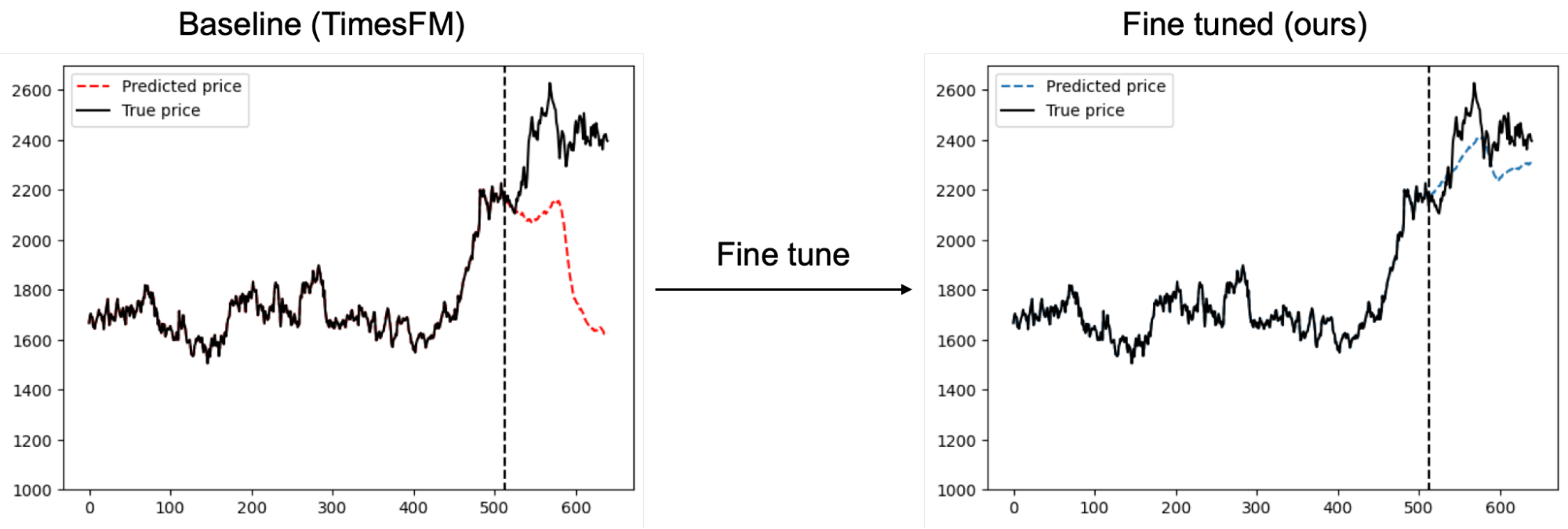
図1:金融データを用いたファインチューニングにより元のTimesFMよりも価格予測精度が向上した例
金融データを用いたファインチューニング
ここでは、まず、使用したデータとファインチューニングの手法・設定について説明します。
データについて
本研究では、TOPIX500構成銘柄の価格時系列を含めた様々なデータを使用しました。詳細は表2の通りです。
| データセット名 | 頻度 | 時系列数 | データポイント数 |
| Topix500 stocks | Daily | 3513 | 2248320 |
| S&P500 stocks | Daily | 3173 | 2030720 |
| Currencies | Daily | 1092 | 698880 |
| Japan Investment Trusts | Daily | 6698 | 4286720 |
| Commodities | Daily | 29 | 18560 |
| Stock Indices | Daily | 216 | 138240 |
| Stock Indices | Hourly | 847 | 542080 |
| Stock prices | Hourly | 31756 | 20323840 |
| Cryptocurrencies | Daily | 1680 | 1075200 |
| Cryptocurrencies | Hourly | 79153 | 50657920 |
表2: データの一覧
性能評価時に未来のデータが学習に使われていることを防ぐために、2022年12月31日までのデータを75:25の比率で学習と評価用に使用し、2023年1月1日以降のデータをテストに使用しました。
ファインチューニングの手法と設定
ファインチューニングとして、金融データを用いたTimesFMの継続事前学習を実施しました。
これは、TimesFMの最終的な重みから金融データをさらに学習する手法であり、一般的なファインチューニング手法です。
これにより、TimesFMをより金融のデータにフィットさせることができると考えられます。
なお、ファインチューニングにあたっては、全ての層の重みをチューニングの対象にしました。
しかしながら、TimesFMをそのまま金融データに適用すると過学習が発生してしまいました。
これは、TimesFMが採用している平均二乗誤差が、時系列間での数値の大きさの差に対して適切にスケーリングされず、数値の大きい時系列に引っ張られて学習が行われてしまうということによるものでした。
そこで、相対平均二乗誤差(percentage MSE)を用いることを試みましたが、フラッシュクラッシュのような極端な事象によりNaNが発生してしまい、学習がうまくいきませんでした。例えば、2000年に東京証券取引所で発生した光通信社の暴落や、2022年の仮想通貨のLUNAの暴落などの事象では、価格変化が10000%を超えており、学習に大きな影響が発生していました。
これらの問題を対処するために、入力データに対して対数変換を行うこととしました。
つまり、
\(y \leftarrow \log(y) \)
という変換を通じて変換を行い、MSEを利用した損失計算を実施し、推論時は逆向きの変換を行うということです。
この変換は、価格変化率の小さい場合には相対平均二乗誤差とほぼ同じ損失関数となりますが、大きな変化に対しては対数的な反応をするため、かなり穏やかな数値となります。
学習の際には、勾配クリッピングを併用することで、さらに学習の安定性を高めました。
学習にあたっては、8枚のV100 GPUと下記のパラメータを用いて学習を行いました。
| Hyperparameter/Architecture | Setting |
| Optimizer | SGD |
| Training epochs | 5 (linear warmup), 95 (cosine decay) |
| Peak learning rate | 1e-4 |
| Momentum | 0.9 |
| Gradient clip (max norm) | 1.0 |
| Batch size | 1024 |
| Max context length | 512 |
| Min context length | 128 |
| Output length | 128 |
| Layers | 20 |
| Hidden dimensions | 1280 |
表3: 学習におけるハイパーパラメータ設定。
学習の効率化のために、入力データと出力データの長さが640になるようにしました。
もし、入力と出力の長さが640に満たない場合には、長さが640になるように入力データを前方向に拡張することで、640の長さに揃ったバッチを作成できるようにしました。
さらに、データ拡張として、TimesFMと同様にマスクを活用します。
例えば、GPU8枚で1024本の時系列のデータを学習する場合、128本の時系列ごとに分割し、各GPUに割り当てます。
その後、[min_context_length, max_context_length]の範囲からランダムにt_endをサンプリングし、次に[0, t_end-min_context_length]の範囲からランダムにt_startをサンプリングします。そして、[t_start, t_end]のポイントを入力として使用します。モデルは、トレーニング中に入力されたポイントから次のoutput_lenのポイントを予測し、損失を評価します。
これにより、学習時のデータセットがランダムに変化することで、過学習を軽減することができます。
結果
このセクションでは、ファインチューニング済みのTimesFMの結果を確認し、他のモデルなどと比較していきます。
学習時の損失
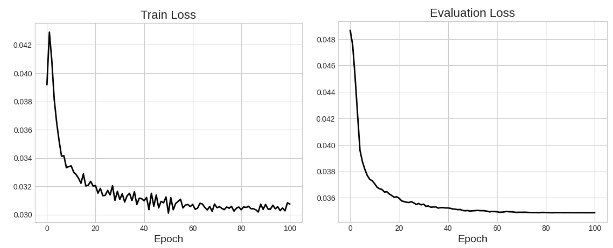
図4: 学習データ(左)と評価データ(右)における学習損失カーブの遷移。損失は学習開始時の70%程度まで低下しています。
図4に示す通り、学習により、損失は開始時の70%程度まで減少し、収束しました。前セクションで説明したランダムマスクの効果もあり、損失カーブにノイズがあるものの、過学習は発生していません。
この結果は、TimesFMが金融データを一定程度学習できていることを示していますが、MSE損失を低下させること自体はそこまで難しいことではありません。学習と評価のデータはどちらも2023年以前の同一期間から抽出しており、データセットが類似しています。
そのため、全体的な市場動向や、価格時系列の類似性を過剰に学習してしまっている可能性があります。
次のセクション以降では、テストセット (2023年以降のデータ) でのパフォーマンスを評価します。
正解率
学習時、モデルにはinput_length<=max_context_length=512個のデータポイント(マスキングあり)が与えられ、次のoutput_len=128個のポイントを予測するというタスクを解いています。
この時、損失はこれらのoutput_lenの全ての点で評価されます。
推論時には、max_context_lengthの点が与えられ(マスキングなし)、次の点を予測するタスクを解きます。出力データ点は必ずしも128点である必要はないですが、今回は予測horizon_lengthを最大128に設定します。
その上で、128点先の価格が1点先の価格よりも上がっているか下がっているかについての正解率を計算することで評価します。
結果は図5の通りで、ファインチューニングにより、ベースとなるTimesFMよりも一貫して高いパフォーマンスを実現できることがわかりました。
比較として、ランダムモデルによるパフォーマンスも計算しました。
ランダムモデルとは、複雑な予測をせずにランダムに出力を出すモデルであり、例えば、テストセット内の価格変動のうち53%が上昇する場合、ランダムモデルは53%の確率で上昇すると予測し、47%の確率で下降すると予測します。
図5の通り、ファインチューニングしたTimesFMは、このランダムモデルよりも性能が良いことが分かりました。
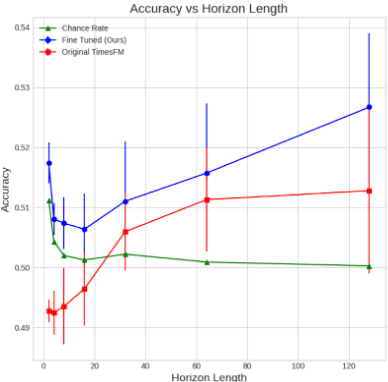
図5:2023年以降のデータを用いたテストセットにおけるup/downの予測精度。Chance Rateとは、テストセットにおけるアップ/ダウンの比率に基づいてランダムな予測を行うランダムモデルの精度である。
トレーディング実験
ここまでで、モデルが予測タスクにおいて、いくつかの比較手法よりも高い性能を出していることが明らかになりました。
このセクションでは、ファインチューニング下TimesFMが取引戦略を通じて利益を得られるかどうかについて分析を行います。
シンプル戦略
この戦略では、終値のみを基に取引を行います。
まず、トレーダーは保有期間を決めます。
これをh=horizon_lenと表します。
以下では、モデルのcontext_lengthをcと表記し、512に設定します。
取引日iの後、トレーダーは入力データとして過去の時系列\(P_{i-c-1:i}=\{P_{i-c-1}, P_{i-c}, \cdots , P_i\}\)をモデルに入力し、\(P_{i+1:i+h}\)の予測を行います。
トレーダーは、取引日i+1とi+hで、以下のように売買注文を出します。
- \(P_{i+h}>P_{i+1}\)の場合、取引日i+1で買い注文、取引日i+hで売り注文を出します。
- \(P_{i+h}<P_{i+1}\) の場合、取引日i+1で売り注文、取引日i+hで買い注文を出します。
この戦略をすべての取引日iに適用します。
もし、合計T資産を取引対象とする場合、すべての注文はバジェットの\(\frac{1}/{hT}\)とします。
これは、取引日の注文のL1ノルムが1/hを超えないようにし、保有期間全体の注文のL1ノルムが1を超えないようにするためです。
まず、2023年1月1日以降のS&P500の日次データを使用した実験の結果を図6に示します。
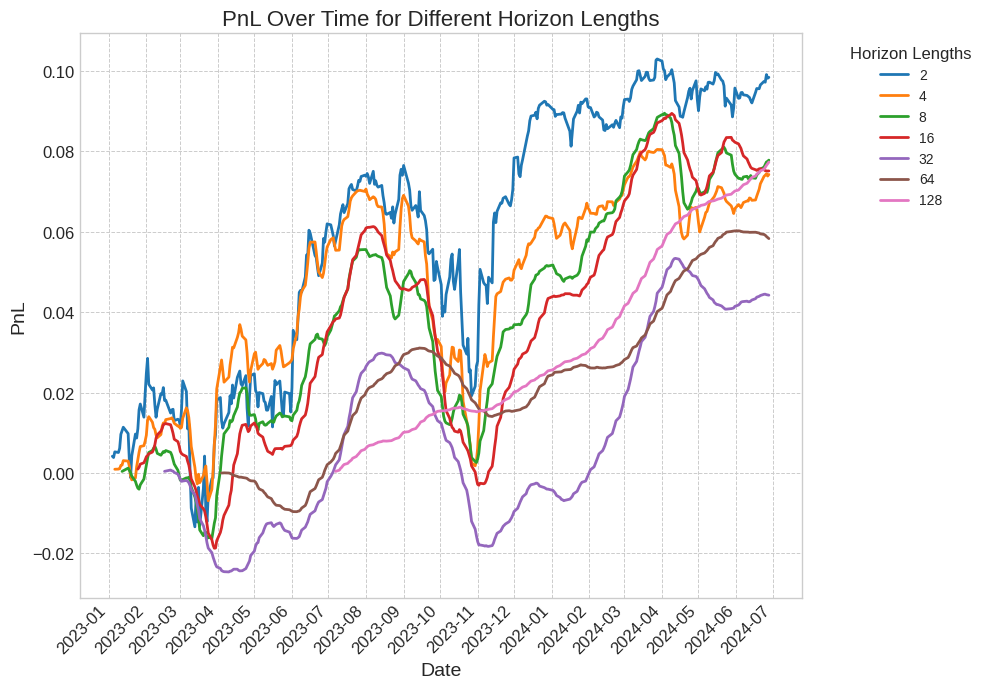
図6: さまざまな保有期間における損益の比較。すべての保有期間でプラスのリターンを達成しています。長めの保有期間にすると、ポジションの変更が少なくなり、より滑らかな結果が得られますが、最初の取引が決裁されるまでの時間が長くなります。
より長い保有期間では、リターンが実現するまでにより長い期間がかかります。
例えば、128の保有期間の場合、最初の注文のポジションを閉じるまでに128取引日待つ必要があります。
そのため、保有期間の違いによってグラフのスタートポイントが違います。
しかし、これらの長い保有期間は、ポジションの変更がはるかに少ないため、はるかにスムーズなPnLグラフをもたらし、取引コストを大幅に削減します。
市場中立戦略
図6を確認すると、保有期間16のPnLで急激な下落が確認できると思います。
これは、市場の全体的な傾向による影響であり、こういった市場による攪乱を削減するために、ここでは市場中立戦略を利用します。
この戦略ではポートフォリオを構築する際に、各取引日における取引対象の平均的な買い/売りバイアスを差し引きます。
これにより、売り買いが同じ金額になるようにすることで、市場中立的なポートフォリオを構築します。
また、一日の取引のL1ノルムが1/hになるように、適切な正規化を行います。
結果として得られるPnLグラフを図7に示します。
また、シャープレシオ、最大ドローダウン、中立コスト(取引シミュレーションの終了時にリターンをゼロになるような必要な取引コスト)などの指標も計算しました。
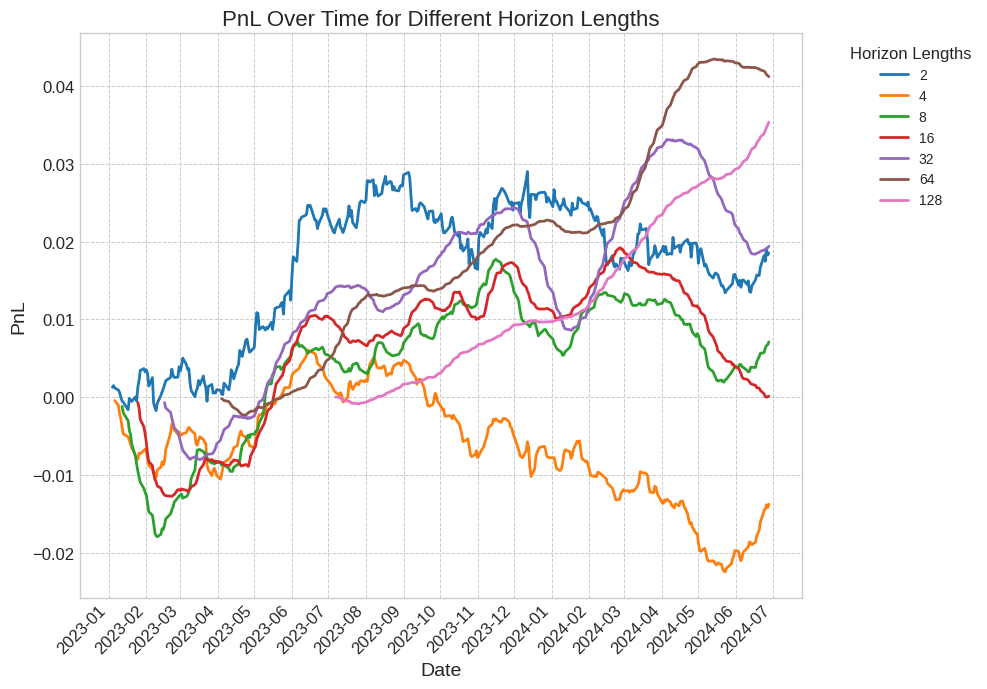
図7: 市場中立戦略を用いた、さまざまな保有期間におけるPnLの比較。図6に比べて、変動が少なくなっていりことが確認できる。保有期間を長くすることで、PnL曲線がより滑らかになり、取引コストが低下することが、表8に示されています。
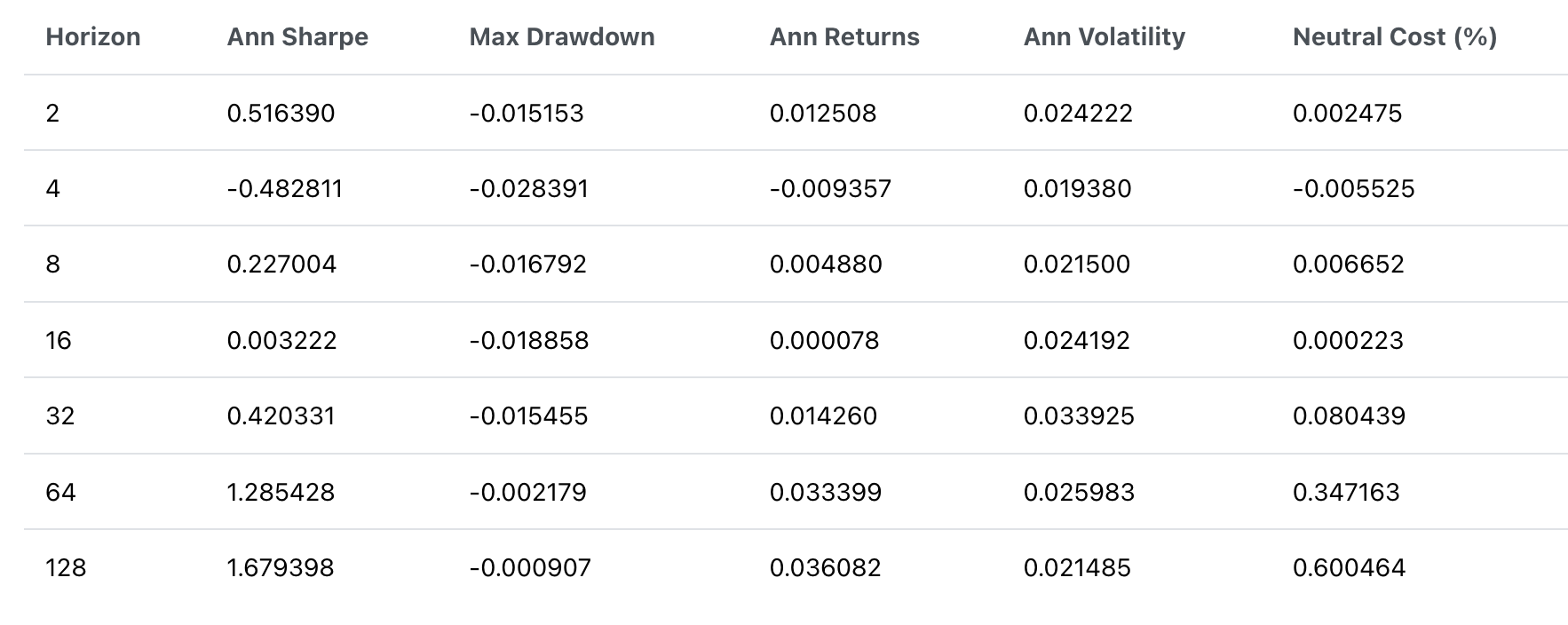
表8: 市場中立戦略の各種指標一覧。保有期間が長くなるほど、年次リターンが向上する一方で、ボラティリティと最大ドローダウンが低下するため、シャープレシオの向上が確認できます。
市場中立のポジションを取ることで、市場全体の動きによる急激な下落をなくすことができます。
その結果、最大ドローダウンの低下とシャープレシオの向上が確認できました。
全体を通じた他のモデルとの比較
ここで、保有期間128に焦点を当て、提案モデルといくつかの他のモデルとを比較します。実験にあたっては、市場中立戦略を用います。
比較手法としては、ランダムモデルとAR1を採用しました。
ランダムモデルとは、全体のデータセット内の上昇率と下落率の比率を最初に計算し、その比率に基づいて、取引日iにおいて\(P_{i+128}-P_{i+1}\) の予測を重み付きのランダムで行います。
AR1(Box 1970)とは、ラグ1の自己回帰モデルで、各時系列に対してトレーニング期間内にモデルを適合させ、テスト期間の予測を行います。その後、平均値を差し引くことで、市場中立の戦略に変換します。
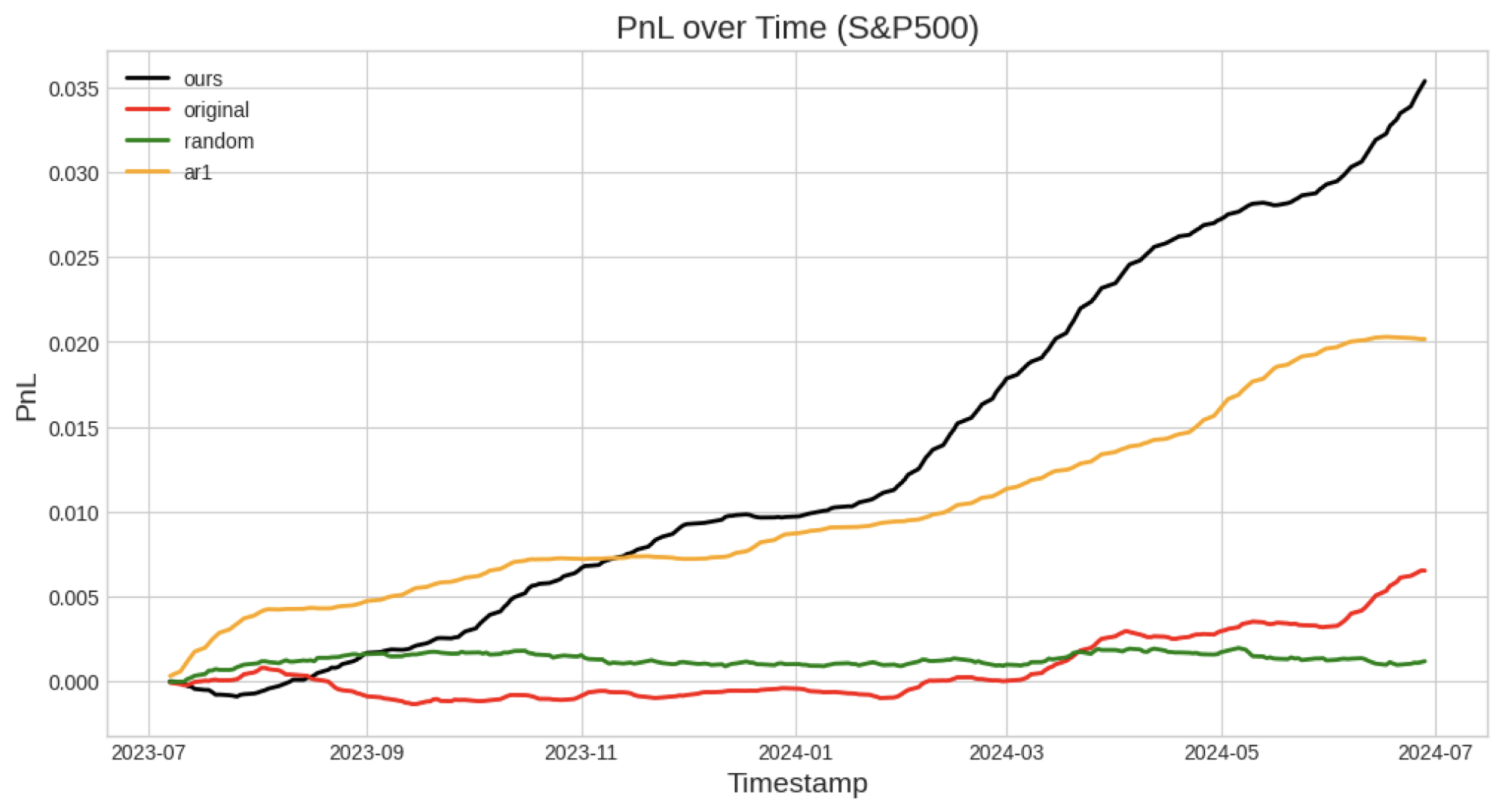
図9:S&P500の株で模擬取引で得られた実現損益のモデル別の比較。
| Ours | Original TimesFM | Random | AR1 | |
| S&P500 | 1.68 | 0.42 | 0.03 | 1.58 |
| TOPIX500 | 1.06 | -1.75 | 0.11 | -0.82 |
| Currencies | 0.25 | -0.04 | -0.03 | 0.88 |
| Crypto Daily | 0.26 | -0.03 | 0.01 | 0.17 |
表10:さまざまな市場におけるシャープレシオの比較。ランダムモデルは、市場中立の設定では有意な結果を得ることができませんが、微調整したTimesFMは、それぞれの市場で最高のパフォーマンスを示しています。
我々のモデルは、すべてのベンチマークでオリジナルのTimesFMを上回りました。
一方で、ランダムモデルは、市場中立戦略では信頼できる予測を行うことができません。
しかし、我々のモデルも為替と暗号通貨のパフォーマンスは、残念ながらあまり良くなっておらず、AR1モデルに大きく負けています。
一方で、我々のファインチューニング下TimesFMは、この中で唯一シャープレシオが1を超えることのできるケースのあるモデルとなりました。
次に、表11では、各手法における中立コストについてまとめています。ここで、スリッページ、取引コスト、およびその他の費用をまとめてコストとしています。
| Ours | Original TimesFM | Random | AR1 | |
| S&P500 | 0.60% | 0.11% | -0.008% | 0.34% |
| TOPIX500 | 0.14% | -0.24% | 0.02% | -0.18% |
| Currencies | 0.08% | -0.017% | -0.008% | 0.27% |
| Crypto Daily | 0.44% | -0.07% | 0.010% | 0.88% |
表11:中立コストの比較。ここでの中立コストとは、取引コスト(割合)のことで、戦略の最終利益をゼロにするために必要なコストを指します。負の値は、その戦略が取引期間中に利益を生み出していないことを示します。
実際の取引にかかるコストの推定は難しく、執行コストや取引手数料、スリッページなど、様々なコストが考えられます。
表11に示すコストの範囲内に抑えることができた場合には、利益が得られることを意味しています。
一方で、負の値は、その戦略が実行された場合、損失が発生することを示します。
私たちのモデルを使えば、最大0.60%の取引コストまでであればでS&P500を取引して利益を得ることができます。
まとめ
このブログでは、時系列基盤モデルのTimesFMを金融データでも使用できるようにするためにファインチューニングを実施しました。
その結果、ファインチューニングしたTimesFMは、いくつかの従来手法をを大幅に上回る結果を達成できることがわかりました。
実験においては、2023年以降のデータを用いて、モデルをテストしました。
モデルの予測に基づいて売買を行う取引戦略を構築して評価したところ、市場中立的な戦略で、長期の保有期間をとる設定においては、いくつかの従来手法を上回るパフォーマンスを発揮しました。
今回の実験のコードは以下のURLで公開しておりますので、是非、参考にしてください。
https://github.com/pfnet-research/timesfm_fin
https://huggingface.co/pfnet/timesfm-1.0-200m-fin