Blog
本記事は、2024年夏季インターンシッププログラムで勤務された畑中さん・沖上さんによる寄稿です。
0. はじめに
はじめまして。2024年度夏季インターンシップに参加した東京大学博士課程2年の畑中樹人と沖上和希です。大学では、畑中は物質に対する有効的なスピン模型を第一原理的に構築するという研究、沖上はトポロジカル磁気構造などの特殊なスピン構造が現れるスピン模型を探索するという研究を行っています。
今回のインターンシップでは、原子位置 \(\{\vec{r}_i\}\) の自由度に加えて、各原子が持っている磁気モーメント \(\{\vec{m}_i\}\) の自由度まで考慮したNeural Network Potential(磁性NNPと呼称)の構築に関して取り組んだので、その内容をご紹介します。
1. 背景と導入
1.1 スピンと磁気モーメント
まず、本稿で取り扱うスピンと磁気モーメントについて簡単に導入をしたいと思います。
スピン自由度とは、各電子が持つ量子力学的な内部自由度であり、スピンアップ (\(\uparrow\)) とスピンダウン (\(\downarrow\)) の2つの状態があります。スピンは角運動量の一つであり、この自由度はスピン角運動量演算子 \(\vec{\hat{S}}\) (以後単にスピンと呼称)の\(z\)成分 \(\hat{S}_z\) の固有値 \(\pm1/2\) に対応しています。
物質中では、一つの原子に複数の電子が存在し、これらはパウリの排他律を満たしながら各軌道に配置されます。その際、電子軌道の充填順序やスピン自由度のとり方は、孤立原子の極限ではフント則(Hund’s rules)に従います。その結果として、各原子が持つスピンの総和 (大きさ) が決まります。
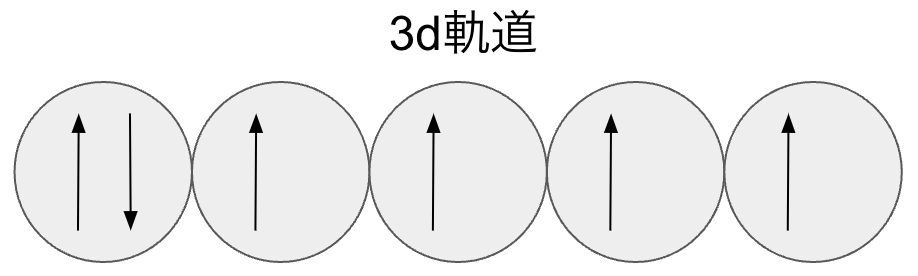
Feにおいて3d軌道に6個ある電子が充填している様子
スピンは角運動量なので、方向を持ちます。大きさ \(S\) のスピンがある方向を向いているとき、\(x,y,z\)軸方向の各成分を求めるには、波動関数に各成分のスピン演算子 \(\hat{S}_x, \hat{S}_y, \hat{S}_z\) を作用させる必要があります。例えば最も簡単な \(S=1/2\) の場合は、各成分がパウリ行列である演算子のベクトル \(\vec{\hat{\sigma}}\) を用いて、スピン演算子は以下のように書くことができます。
$$
\vec{\hat{S}} = \frac{\hbar}{2}\vec{\hat{\sigma}}
$$
このような演算子を用いるとスピン自由度は厳密に取り扱うことができますが、この方法では自由度が非常に大きくなり、実際の物質サイズの系を取り扱うことはできません。そのため、今回取り扱うスピンは量子力学的演算子としてのスピンではなく、以下の図および式に示すような各原子が持つ大きさ\(S\)のdipol
$$
\vec{S} = S\vec{e}
$$
ここでスピンの単位方向ベクトルを \(\vec{e}\) としています。
実際の物質では、各原子のスピンそのものではなく、磁気モーメントに興味がある場合があります。この磁気モーメント \(\vec{m}\) はスピン \(\vec{S}\) に加えて軌道角運動量 \(\vec{l}\), そしてボーア磁子 \(\mu_{\text{B}}\) を用いて以下のように表されます。
$$
\vec{m} = -\mu_{\text{B}}(\vec{l}+2\vec{S})
$$
以後、本稿ではこのようにして求まる磁気モーメントの自由度を取り入れたNNPについて考えていきます。
各原子上のスピンのイメージ図。[1]より引用。
1.2 NNPの現状とスピン自由度
物質のエネルギーなどを量子力学的な精度で計算するために、これまで密度汎関数理論 (Density Functional Theory, DFT) がよく用いられてきました。しかし、大規模な系の計算や、古典的な分子動力学と組み合わせた長時間の第一原理分子動力学計算においては、DFTの計算コストが課題となっています。
そこで、DFTの結果を学習することで、DFTの計算をNeural Networkで置き換えるというNNPの研究が近年盛んに行われています。DFTが良く学習されたNNPに置き換わることで、精度を犠牲にせずに計算可能な系のサイズやタイムスケールが飛躍的に高めることができ、Matlantis™内部でもNNPが用いられています[2]。
これまで、NNPでは通常各原子の原子番号 \(\{Z_i\}\) とその位置 \(\{\vec{r}_{i}\}\) のみをインプットにして学習してきました。また、そのダイナミクスの計算には各原子の質量 \(\{M_i\}\) を用いて以下のように分子動力学 (Molecular Dynamics, MD) が用いられています。
$$
M_i\frac{\partial^2\vec{r}_i}{\partial{t}^2} = -\frac{\partial E(\{Z_i\}, \{\vec{r}_i\})}{\partial \vec{r}_i}
$$
これらの自由度に加えて、磁性体中では各原子が磁気モーメント\(\vec{m}_i\)を持ちます。ここで、\(\vec{m}_i\)は先ほど導入した通り量子力学的演算子ではなくベクトル量で表されるdipoleモーメントであるとします。物質中では電子を媒介として\(\vec{m}_i\)間にも相互作用が働き、\(\vec{m}_i\)にもダイナミクスが生まれます。そのスピンのダイナミクス (Spin Dynamics, SD) を記述する方程式として以下で表されるランダウ-リフシッツ-ギルバート (Landau–Lifshitz–Gilbert, LLG) 方程式があります。
$$
\frac{\partial\vec{m}_{i}}{\partial t} = -\gamma\vec{m}_{i}\times\vec{B}^{\textrm{eff}}_{i}+\frac{\alpha}{|\vec{m}_{i}|}\vec{m}_{i}\times\frac{\partial \vec{m}_{i}}{\partial t}\\
\vec{B}^{\textrm{eff}}_{i} = -\frac{\partial E(\{Z_i\}, \{\vec{r}_i\}, \{\vec{m}_i\})}{\partial\vec{m}_{i}}
$$
ここで、\(\gamma\)は磁気回転比とよばれる物理定数で、\(\alpha\)はギルバート減衰定数と呼ばれるスピンについての緩和の速さを表す無次元量です。また、下段で示されているスピンに対して有効的に働く磁場\(\vec{B}^{\textrm{eff}}_{i}\)を、原子位置に作用するforceにちなんで以後magnetic forceと呼びます。
大規模な系に対して、原子位置 \(\vec{r}_i\) に加えてスピン \(\vec{m}_i\) の自由度も考慮したエネルギー\(E(\{Z_i\}, \{\vec{r}_i\}, \{\vec{m}_i\})\)を計算できるようになると、MDとSDを組み合わせたシミュレーションが可能になります。このシミュレーションによって、原子配置と磁化過程が密接に絡み合った磁歪現象であったり、磁性体の有限温度特性をより良くシミュレートする・理解することができるようになります。また、ダイナミクスに限らずとも、任意の原子配置に関して最も安定なスピン構造をDFT計算を抜きにして探索することができるようになるという利点もあります。
そこで、本インターンではスピン自由度も考慮した磁性NNPを構築するという課題に取り組み、スピン模型から作成した人工データセットの学習に成功しました。インターン期間の都合上、実際にDFTで作成したデータセットでテストすることはできませんでしたが、本稿ではその作成過程および構築した磁性NNPをご紹介します。
2. SDFTによるデータセット作成
通常のDFTでは電子の密度分布\(\rho(\vec{r})\)に関する自己無撞着方程式であるコーン–シャム方程式を解きます。このコーン–シャム方程式において、波動関数にスピン自由度 (\(\sigma=\uparrow, \downarrow\)) を導入したものをスピン偏極DFT(spin-poralized DFT, SDFT)といいます。このSDFTではコーン–シャム方程式を解いた結果の固有状態 (コーン–シャム軌道) \(\psi_{n\sigma}\) から、以下のようにして磁気モーメントの空間分布関数 \(\vec{m}(\vec{r})\) が計算されます。
$$
\vec{m}(\vec{r}) = -\mu_{\text{B}}\sum_{n\in\text{occupied orbitals}}\sum_{\sigma\sigma’}\psi^{\ast}_{n\sigma}(\vec{r}){\vec{\hat{\sigma}}}_{\sigma\sigma’}\psi_{n\sigma’}(\vec{r})
$$
この \(\vec{m}(\vec{r})\) を各原子 \(i\) ごとの寄与に分解することで各原子のスピン \(\{\vec{m}_i\}\) が決まります。
本節では、磁性NNPを構築する際にSDFTでどのように教師データを作成するかという点について述べます。本稿ではDFTのソフトウェアとしてVASP[3]を用いており、計算する物質としてはBCCおよびFCCのFeとしています。また、格子定数はそれぞれ2.86, 3.66 Åとしました。また、データセットの構成や作成手順については[4]を参考にしています。
2.1 constrained-DFT
SDFTにおいてベースになっているホーエンベルグ–コーンの定理は基底状態に対して成り立つ定理です。そのため、下の概念図に示すようにスピン構造に関する広いパラメータ空間の中で少なくとも局所最適でないとその磁気構造に収束してくれません。
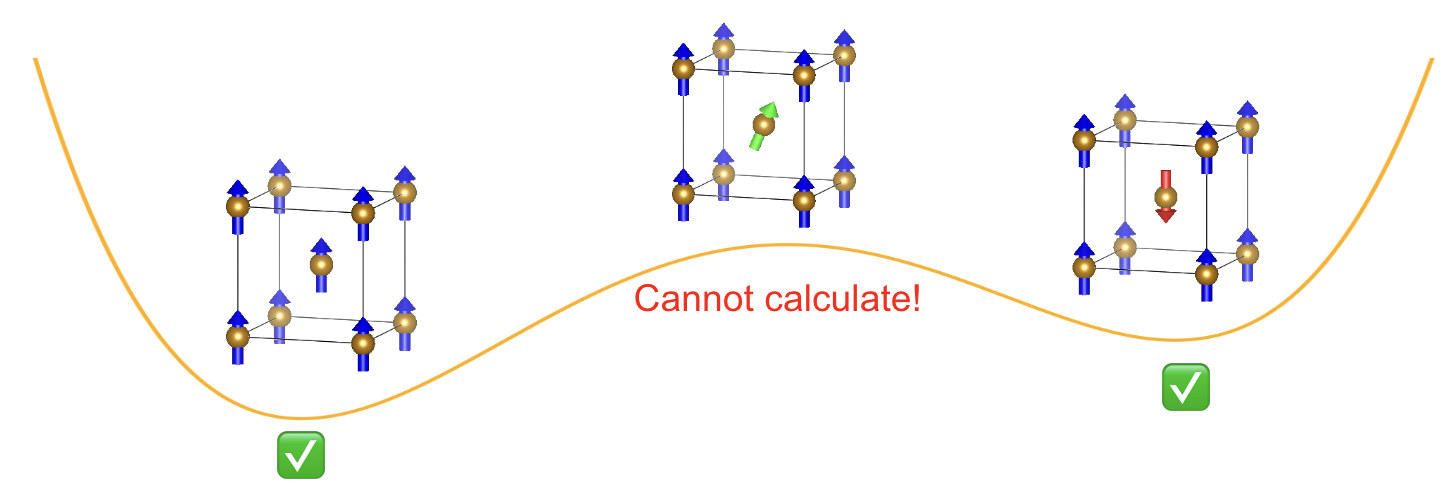
通常のSDFTのスピンに対するエネルギー曲面。横軸がスピン構造で縦軸がエネルギーであり、局所最適でないスピン構造は計算できません。
しかし、磁性NNPを学習させるためには必ずしも局所最適でないようなスピン構造も学習点に含める必要があります。そこで、通常のSDFTでは収束しないようなスピン構造に収束させてエネルギー等を計算したい場合があります。そのような場合に用いられるものがconstrained-DFT (cDFT) です。cDFTでは、本来収束しないような磁気構造に半ば無理やり収束させるためにSDFTの自己無撞着ループの中で最小化されるエネルギーに人為的なペナルティ項 \(E_p\) を付け加えた目的関数を最適化します。
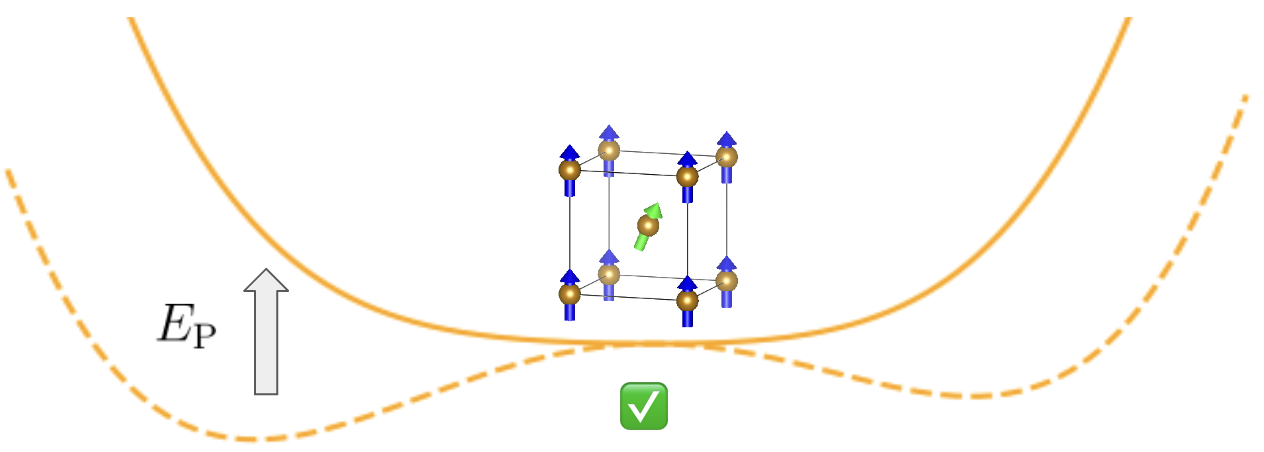
cDFTのイメージ図。もとのエネルギー曲線 (破線) に対してペナルティ項 \(E_p\) を付け加えた目的関数 (実線) では収束させたいスピン構造が最小値になっています。
このペナルティ項はいくつか種類がありますが、その表式によって磁気モーメントに対してどのようなconstraintを課すかが変わってきます。具体的にはSDFTの結果の磁気モーメント\(\vec{m}_i\)と収束させたいモーメント\(\vec{m}^{\textrm{con}}_i\)、そしてconstraintの強さを表すパラメータ\(\lambda\)を用いて以下のような表式があります[5]。
| constraint type | constraintの内容 | \(E_p\)の表式 |
|---|---|---|
| 1 | momentの方向のみ | |
| 2 | momentの方向と大きさ |
\(\sum_i\lambda\left(\vec{m}_i-\vec{m}^{\textrm{con}}_i\right)^2\)
|
| 4 | momentの方向とその符号 |
constraint typeのラベルに関してはVASPにおけるINCARタグに従っています。
2.2 \(\lambda\) に対する \(E_p\) の収束
複数のスピン構造に対してcDFTで計算されたエネルギーを比較するために、出来るだけ\(E_p\)の影響を取り除かなければいけません。そのために、cDFTを行う場合は\(E_p\)が十分に0に近づいていることを確認しなければなりません。
cDFTで導入されたペナルティ項 \(E_p\) は、収束先のモーメントがconstraintを完全に満たしていれば0になります。しかし、constraintの強さを表すパラメータである \(\lambda\) が小さい時には必ずしもconstraintを満たしてくれません。その一方で、\(\lambda\) が十分に大きい場合に関しては、理想的な条件の下では \(E_p\) は漸近的に以下のように振る舞うとされています[5]。
$$
E_p \propto\frac{1}{\lambda}\rightarrow 0\ \ (\lambda\rightarrow\infty)
$$
constraintなしのSDFTのSCFループはエネルギーの最小化問題ですが、cDFTで求めたい解は拘束条件の下でのエネルギーの最小化問題です。cDFTのペナルティ項に含まれる \(\lambda\) はその拘束条件に対するLagrange乗数であると捉えることができます。そのため、一般にはこの \(\lambda\) についても最適化問題を解いてその値を決めなければいけません。
しかし、これはSDFTにおいては非常に難しい問題です。先に述べたように \(\lambda\) が十分大きければ漸近的にはconstraintをほとんど満たすようになると期待されますが、数値計算上は不安定になります。良くとられる戦略の一つは \(\lambda\) を変化させて計算を行い、 \(E_p\) が十分小さくなるような \(\lambda\) の値を決めるという方針です。
そこで、今回の計算においてもこの方針に基づいて \(\lambda\) を決定しました。\(\lambda\) 決定のために計算は以下のようなBCCのconventional cellに含まれる2原子のスピンの相対的な角度を変化させた構造 \((\theta=0, \pi/4, \pi/2, \pi)\) を用いて確認しました。
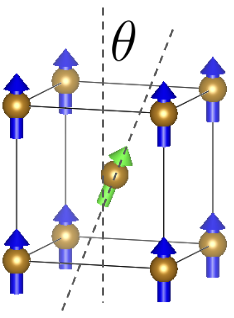
BCCのconventional cellで2原子の相対角度を変化させた構造。
以下の左図に、磁気モーメントの方向のみにconstraintをかけるタイプ1において \(\lambda\) を大きくしていった際の \(E_p\) の収束の様子、また右図には\(\theta=\pi/4\)の場合にcDFTの結果とconstraintをかけているモーメントの方向がなす角 \(\Delta\theta\) を示しています。
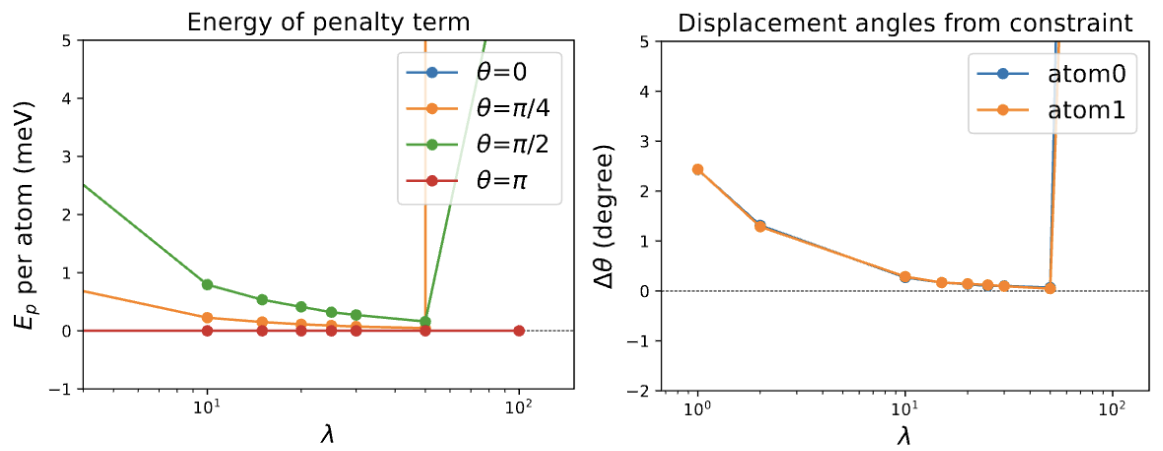
\(\lambda\) の変化に対する\(E_p\) の収束の様子 (左) および\(\theta=\pi/4\)に対するcDFT結果とモーメント方向がなす角\(\Delta\theta\) (右)。
\(E_p\) は、通常NNPの誤差として典型的なスケールである数meVよりも十分小さくなっていれば良いと考えることができます。左図を見ると \(\lambda\) を大きくすると\(E_p\)が0に向かって収束している様子が見てとれます。また、 \(\theta=0,\pi\) といったそもそも良い収束先になっている構造に対しては、 \(\lambda\) が小さくても \(E_p=0\) となっていることも分かります。ただし、 \(\theta=\pi/4,\pi/2\) といったconstraintをかけないと収束してくれない磁気構造に対して\(\lambda=100\)のように大きくしすぎると数値的に不安定になり必ずしも望みのスピン構造に収束してくれていないことも分かります。
他のconstraint typeや、最初から最後まで一つの\(\lambda\)で計算するのではなく計算が進むにつれて\(\lambda\)を変化させるという方法も試しましたが、収束の良さ及び計算時間の観点から以後の計算は全てconstraint typeは1 (モーメントの方向のみに制限をかける) でかつ \(\lambda=50\) としました。
2.3 制限磁場とMagnetic force
ここまでで、エネルギーは2.1で導入したcDFTによって計算できることが分かりました。では、1.2で紹介したLLG方程式に登場するmagnetic forceも含めて学習したいときに、こちらはどのように教師データを作成できるでしょうか。
cDFTで加えたペナルティ項は、SDFTにおいて各原子の磁気モーメントに対して新たに有効的に磁場を加えることに対応します。その有効的な磁場を制限磁場 \(\vec{B}^{\textrm{con}}_i\) とすると、実はこの制限磁場とmagnetic forceは強く関係しています。その関係を数式で表すと以下のようになります[6]。
$$
\vec{B}^{\textrm{eff}}_{i} = -\vec{B}_{i}^{\text{con}} – \frac{1}{|\vec{m}_i|} \left\langle \nabla_{e_i}^* \hat{H}_{\text{KS}} \right\rangle \tag{*}
$$
厳密に逆向きというわけではありませんが、右辺第二項の補正項を伴ってほとんど逆向きの量として紐付いていることがわかります。ここで右辺第二項は、コーン–シャムハミルトニアンを、電子密度と磁気モーメントの大きさを保ちながら方向についてのみ微分 \(\nabla_{e_i}^*\) をとり、元の固有状態で期待値を取ったものになります。詳細は省きますがこの項は、SDFTにおいてスピン構造が変わるとその自己無撞着解も変化し、その結果としてハミルトニアン自体が変化するために発生する項になります。
式で書くと以下の項が非ゼロになることで発生する項です。
$$
\nabla_{e_i} \hat{H}_{\text{KS}} \neq 0
$$
この第二項は多くの場合第一項に対して値が小さく、実際にFeのdimerで2スピンの相対角度\(\theta\)を変化させた時の\(\vec{B}^{\textrm{eff}}_{i}\)と\(\vec{B}^{\textrm{con}}_{i}\)の比較結果を以下の図に示すと、主要項である右辺第一項に対して、右辺第二項の影響が比較的小さいことが分かります。SDFTでは第二項が非ゼロになりますが、平均場的に決まるパラメータを含まない \(\nabla_{e_i} \hat{H} = 0\) を満たすようなハミルトニアン\(\hat{H}\)に対しては第二項は常にゼロになります。
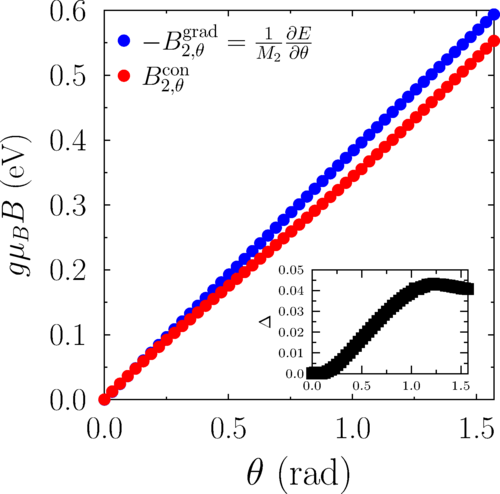
Fe dimer系でのmagnetic forceと制限磁場の比較結果。[6]より引用。
式 \((*)\) の関係のイメージを以下の図に示します。制限磁場がないとmagnetic forceが働いて磁気モーメントが変化するところを、制限磁場によって無理やり望みのモーメントにしているので、この二つがほとんど釣り合っていると考えることができます。この描像は、右辺第二項は十分に小さいときに成り立ちます。従って、magnetic forceを教師データに含めたい場合はcDFTの結果として得られる制限磁場を逆向きにすれば良いことがわかります。
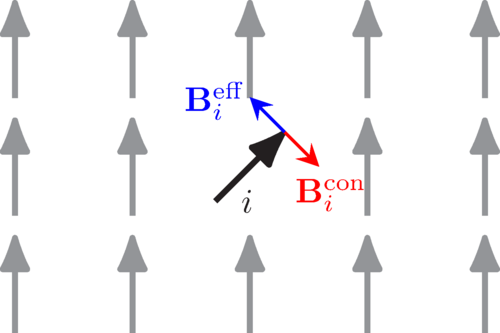
magnetic force(青)と制限磁場(赤)の関係のイメージ図。[5]より引用。
しかし、magnetic force \(\vec{B}^{\textrm{eff}}_{i}\)と制限磁場 \(\vec{B}_{i}^{\text{con}}\)が厳密には同じではありません。これはエネルギーとその微分として与えられるmagnetic forceが整合しないという点でNNPを学習する際に妨げとなる可能性があります。
そこで、今回は先ほどと同じくBCCのconventional cellで2原子の相対的な角度を変化させた時に、cDFTの制限磁場と有限差分によるmagnetic forceが数値的にどのように異なるかを確認しました。
結果を以下に示します。ここで、magnetic forceは以下のような有限差分の式で求め、\(\delta\theta=5\) deg としました。
$$
f'(\theta) \simeq \frac{f(\theta+\delta\theta)-f(\theta-\delta\theta)}{2\delta\theta}
$$
|
\(\theta\)
|
magnetic force \(\vec{B}^{\textrm{eff}}_{i}\) (eV/\(\mu_{\textrm{B}}\))
|
制限磁場 \(\vec{B}_{i}^{\text{con}}\) (eV/\(\mu_{\textrm{B}}\)) |
|---|---|---|
| 0 | 0.0024 | 0.0000 |
| \(\pi/4\) | 0.1681 | 0.1636 |
| \(\pi/2\) | 0.2993 | 0.2913 |
有限差分による誤差もありますが、確かにこれら二つが異なっていることが分かります。今回は制限磁場の逆向きをmagnetic forceとしたデータセットに対して磁性NNPを適用するまでに至らなかったのでこの差異が学習にどの程度効いてくるのかは検証できていませんが、シミュレーションしたい現象や系のエネルギースケールによっては無視できない影響を与えうるので、教師データをcDFTを用いて作成する際は注意が必要です。
2.4 データセット作成
これまでに決定した計算条件のもとで実際にデータセットを作ります。BCCとFCCに対してそれぞれ作成したデータセットを以下に示します。
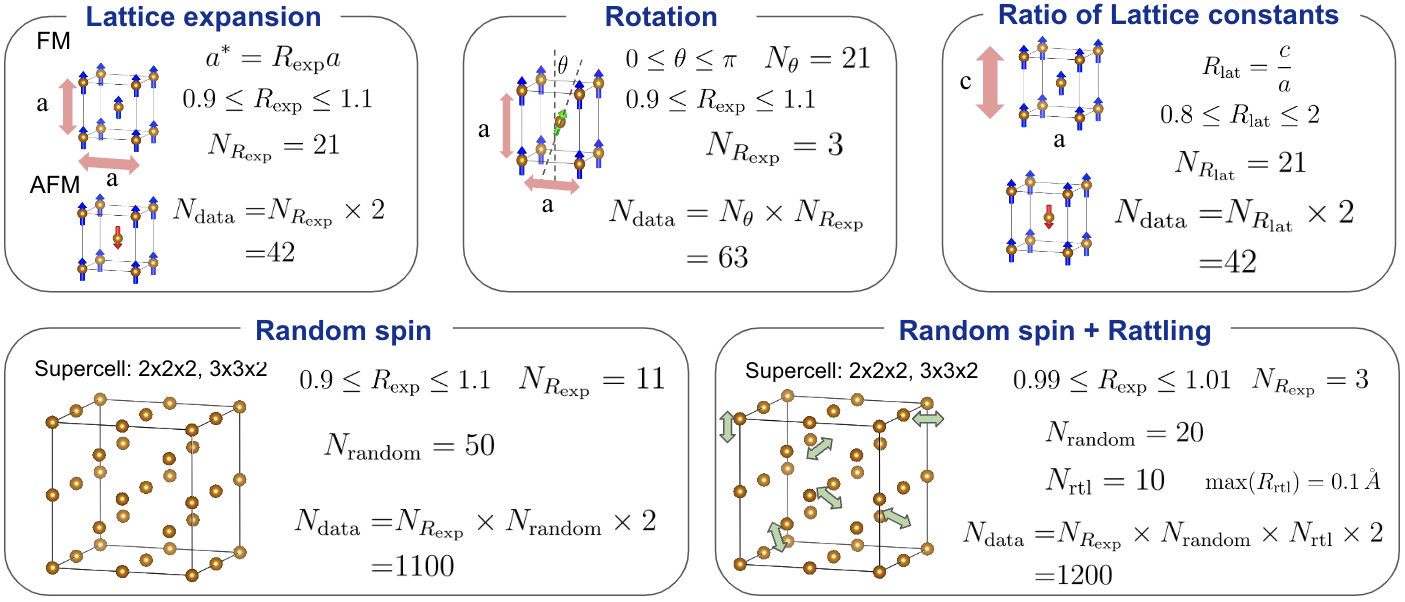
BCCに対するデータセット。
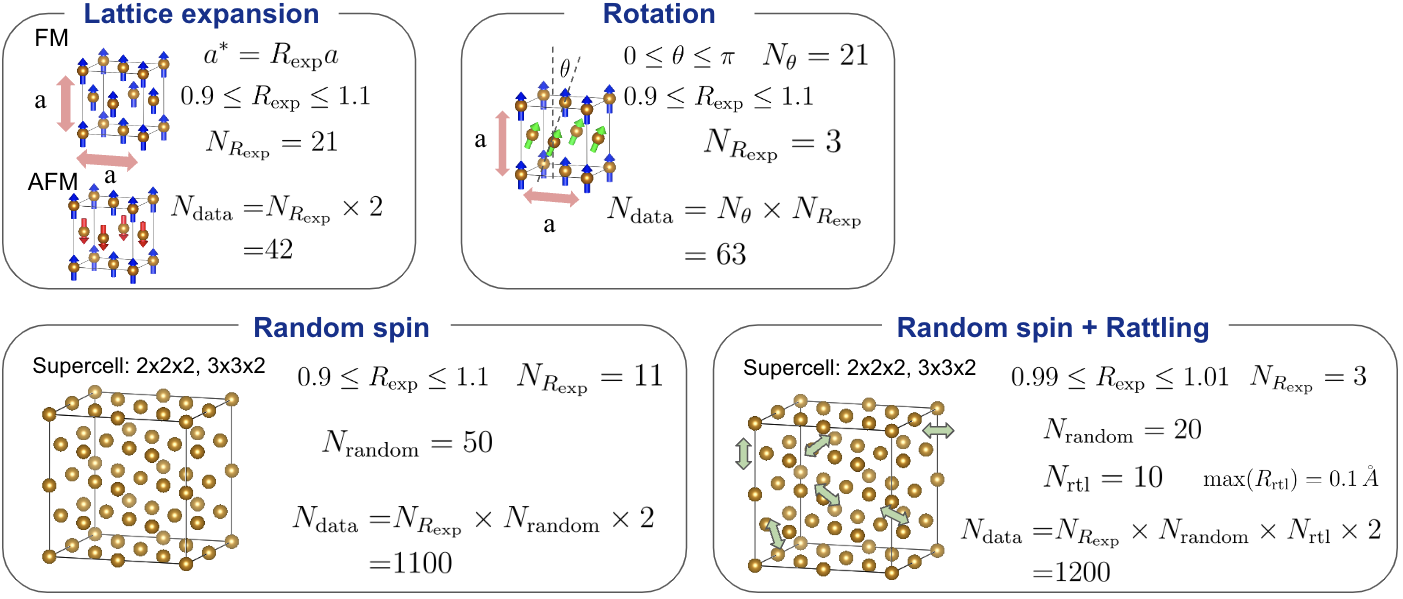
FCCに対するデータセット。
図中にあるパラメータはそれぞれ以下のように定義されています。また、下段のRandom spinそしてRandom spin + Rattlingでは計算資源の都合でprimitive cellのsupercellをとっています。
| パラメータ | 内容 |
|---|---|
| \(R_{\textrm{exp}}\) | 格子定数を定数倍する際の比率 |
| \(R_{\textrm{lat}}\) | a軸方向とc軸方向の格子定数比 |
| \(\max(R_{\textrm{rtl}})\) | 原子位置にrattlingを加える際の最大変異量 (Å) |
| \(N_{\textrm{exp}}\) | 図中で指定された\(R_{\textrm{exp}}\)の範囲を均等に何点に区切ってサンプリングするか |
| \(N_{\theta}\) |
$latex 0\leq\theta\leq\pi$を均等に何点に区切ってサンプリングするか
|
| \(N_{\textrm{random}}\) | スピン構造をランダムに何個サンプリングするか |
| \(N_{\textrm{rtl}}\) | ランダムなrattlingを何個サンプリングするか |
| \(N_{\textrm{data}}\) | 区切ってあるデータのまとまりが何個構造を持つか |
今回は結局時間の都合で次節で作成するスピン模型によるデータセットにのみ適用したので、このデータセットによる検証はできていません。実際にこのデータセットを用いるときは、必ずしも全ての計算でcDFTのconstraintを十分に満たしているとは限らないことに注意が必要です。そのため、\(E_p\)や実際に磁気モーメントがconstraintの向きを向いているかどうかを確認し、データとして篩にかけなければいけません。
3. スピン模型によるデータセットの作成
前節ではFeに対してcDFTによってデータセットを作成しましたが、その際制限磁場の逆向きをmagnetic forceとして用いることでエネルギーとその微分値が整合しなくなり、学習に影響がある可能性について言及しました。その問題を回避するために、原子配置は2.4で作成したデータセットと同じものですが、スピン構造によるエネルギーの寄与はSDFT計算ではなくスピン模型で計算されるようなデータセットを作成しました。このデータセットにおいて、エネルギーはPFP[2]によって計算された原子配置の寄与と、スピン模型から計算されるスピン構造の寄与との合計として求められます。このデータセットでは、magnetic forceを解析的に計算することができるため、2.3で述べたようなSDFTでは発生しうる微分値としての整合性の問題が発生せず、4節で導入する磁性NNPのベンチマークに適しています。
3.1 スピン模型
ミクロな電子などの自由度ではなく、磁気モーメント間を単にベクトルとしてその間の相互作用をモデル化したものを古典スピン模型といいます。今回は、磁気モーメントの配列から以下のようにエネルギーが計算される模型を用います。
$$
E(\{\vec{m}_i\}) = – \sum_{i \neq j}^{N} J(|\vec{r}_{ij}|) \left[ \vec{m}_i \cdot \vec{m}_j – 1 \right] – \sum_{i \neq j}^{N} K(|\vec{r}_{ij}|) \left[ \left( \vec{m}_i \cdot \vec{m}_j \right)^2 – 1 \right]
$$
このモデルは、最も基本的な相互作用であるHeisenberg相互作用 \(J(|\vec{r}_{ij}|) \vec{m}_i \cdot \vec{m}_j\) に、より高次の項であるBiquadratic相互作用 \(K(r_{ij}) (\vec{m}_i \cdot \vec{m}_j )^2\) を加えたものになります[7]。
また、原子配置の効果を取り入れるために、\(f(r)\) の形をとるこれらの相互作用が距離 \(r\)に従って以下のように変化するとします。
$$
f(r) = 4\alpha \left( \frac{r}{\delta} \right)^2 \left( 1 – \gamma \left( \frac{r}{\delta} \right)^2 \right) e^{-\left( \frac{r}{\delta} \right)^2} \Theta(R_c – r)
$$
ここで、\(\alpha\) を相互作用のエネルギースケール、\(\delta\)を相互作用が減衰する典型的な距離スケール、\(\gamma\) を無次元の曲率パラメータ、そして \(\Theta(R_c-r)\) をカットオフ半径\(R_c\)の元でのHeavisideステップ関数とします。
カットオフ半径 \(R_c = 5\) Åに加えて、それぞれの相互作用\(J(r), K(r)\)についてのパラメータ群は以下のように設定しました[7]。
| 相互作用 |
\(\alpha\) (eV)
|
\(\gamma\)
|
\(\delta\) (Å) |
|---|---|---|---|
|
\(J(r)\)
|
0.2827 | -4.747 | 0.7810 |
|
\(K(r)\)
|
0.03619 | -2.973 | 0.5273 |
このパラメータの下で、\(J(r), K(r)\)の距離依存性は下図のようになります。典型的な値として格子定数 \(a=2.86\) Åの場合の最近接 (Nearest Neighbor, NN) の原子間での値 (\(\sqrt{3}a/2\simeq 2.48\) Å) を赤の縦破線で示しています。
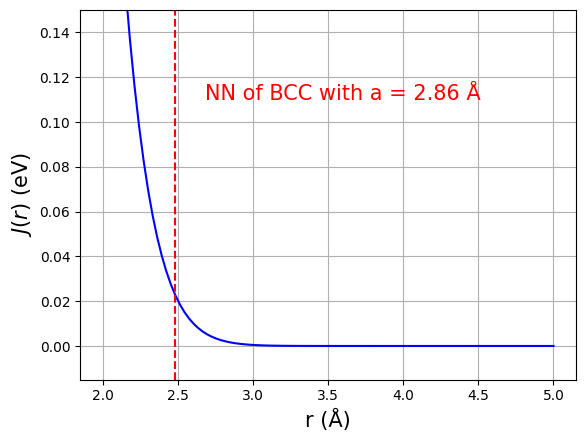
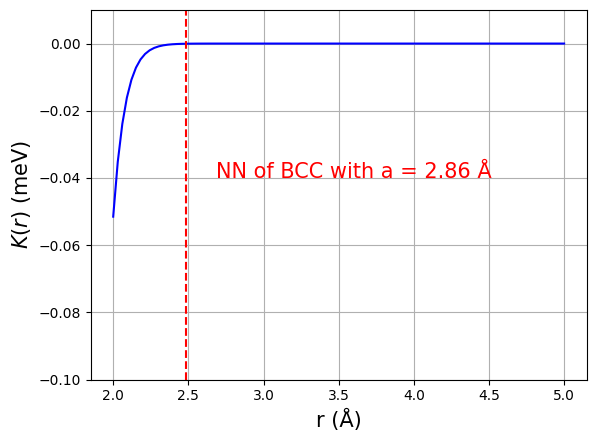
上記パラメータの下での\(J(r), K(r)\)の距離依存性。
相互作用が距離に対して強く減衰しており、かつBiquadratic相互作用の大きさ \(|K(r)|\) は \(|J(r)|\) に比べて非常に小さいことが分かります。
3.2 データセット作成
2.4で作成したデータセットの原子構造とスピン構造、そして前項で定義したスピン模型を用いてデータセットを作成しました。エネルギーの計算は次の通り行います。エネルギー全体を原子構造の寄与とスピン構造の寄与に分けたときに、前者をPFP[2]で、そして後者を前項で定義したスピン模型で計算し、その総和をその構造のエネルギーとします。BCCのconventional cellで2原子の相対的な角度を変化させた構造に対して、上記の方法でエネルギーを計算したものを下図に示します。
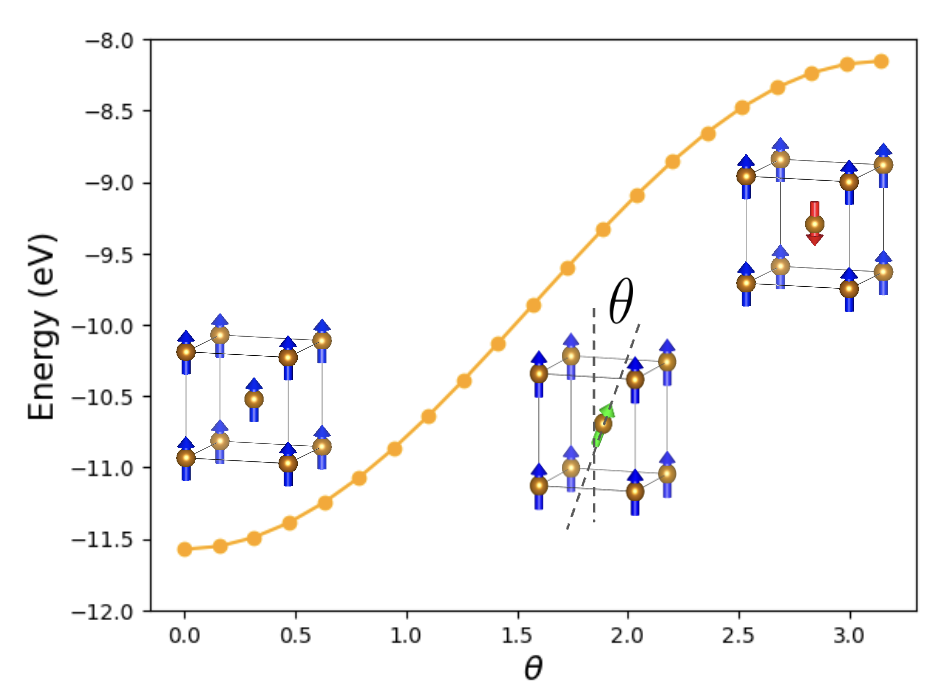
磁気モーメントの相対角度に対するエネルギー。
今回は \(J(r)>0\)である強磁性的な相互作用のパラメータを用いているので、強磁性配列の方がエネルギーは低く安定です。また、スピン構造によって最大1 eVスケールで値が変化することがわかります。
4. スピン構造の自由度も考慮したNeural Network Potential
4.1 不変性と同変性
NNPを考えるときに、インプットとなるのは通常、物質の構造 (原子番号\(\{Z_i\}\) とその位置 \(\{\vec{r}_{i}\}\)) です。そして、与えられた構造に対してNeural Network \(f\)がエネルギー \(E=f(\{Z_i\}, \{\vec{r}_i\})\) を出力するとします。原子が位置している三次元ユークリッド空間での並進操作を\(\mathscr{T}\)、回転操作を\(\mathscr{R}\)とすると、通常はこれら\(\mathscr{T},\mathscr{R}\)に対して以下のようにエネルギーが不変であることを要請します。
$$
f(\{Z_i\}, \{\vec{r}_i\}) = f(\{Z_i\}, \mathscr{T}\{\vec{r}_i\}) = f(\{Z_i\}, \mathscr{R}\{\vec{r}_i\})
$$
この不変性 (Invariance) の拡張として同変性 (Equivariance) があります。具体的に数式で表すと、空間 \(X\) から空間 \(Y\) への写像 \(f: X\rightarrow{Y}\)、そしてある群 \(G\) とその元 \(g\in{G}\) に対して空間 \(X,Y\) での表現行列を \(D_X(g), D_Y(g)\) とした時に以下のようになります。
$$
\forall g\in{G},\ \ f(D_{X}(g)x) = D_Y(g)f(x)
$$
以上の式を見ても分かるように、同変性は不変性とは違い、インプットに対してある操作を加えたときに出力は変化しても良いが、入力と出力の変換性が同様に群の表現に従うというものです。ここで、不変性は同変性に内包される概念であることに留意します。不変性は同変性の特別な場合であり、より強い制限となっているため、より多くの対称操作に関する情報が失われてしまいます。そこで同変性を用いることで、写像 \(f\) を作用させた後も対称操作に関する情報を伝えることができます。
4.2 SO(3)とその既約表現
では実際にインプットの構造に対する同変性を考えていきます。まず、インプットの構造に対して座標の絶対値ではなく各原子間の相対位置 \(\{\vec{r}_{ij}=\vec{r}_i-\vec{r}_j\}\) を用いてembedすることで、並進操作\(\mathscr{T}\)に対しては不変性を課すことにします。
次に、それ以外の操作を考えます。三次元空間における回転操作や反転操作など、ある固定された原点からの長さや角度を保ったまま3次元空間の座標を変換する操作は直交群O(3)を成します。このO(3)は、表現行列の行列式が1である特殊直行群SO(3)と、空間反転操作 \(I\) に対する \(Z_2\) インデックスの直積に分解することができます。
$$\textrm{O(3)} = \textrm{SO(3)}\times Z_2$$
そしてSO(3)の既約表現は非負整数 \(\ell\) で特徴づけることができ、そしてその表現行列は \(2\ell+1\) の次元を持ちます。ここで、各量子数 \(\ell\) の球面調和関数 \(Y^\ell:S^2\rightarrow\mathbb{R}^{2\ell+1}\) を、\(m = -\ell, -\ell+1, \dots, \ell-1, \ell\) に対して \([Y^\ell(\vec{r})]_m = Y^\ell_m(\vec{r})\) となる写像と定義します。このように定義された球面調和関数はSO(3)に対して同変となります。従って、相対位置 \(\vec{r}_{ij}\) や磁気モーメント \(\vec{m}_i\) などの方向を持つ量を球面調和関数を用いて変換することで、特徴量に変換した後も物理的な対称性を伝えることができます。具体的には、\({Y}^{\ell}(\vec{r}_{ij})\) に対する同変性は以下のように表されます。ここで、\(\mathscr{R}\) をSO(3)の元 \(R\) に対する回転行列、そして \(D^{\ell}(R)\) をWignerのD行列とし、以後ベクトル \(\vec{x}\) を大きさ1に規格化したものを \(\hat{x}\) と表記します。
$$
Y^{\ell}(\mathscr{R}\hat{r}_{ij}) = D^{\ell}(R)Y^{\ell}(\hat{r}_{ij})
$$
このようにして、同変性のある写像で特徴量に変換することで、物理的な対称性を特徴量にも反映させることができますが、最終層の出力であるエネルギーはこの後に導入する空間反転や時間反転操作で変化しない \(\ell=0\) のスカラー量です。スカラー量であるエネルギーは、構造全体の回転操作によって変化しないことを要請するので、エネルギーに対しては不変性を要請していることになります。しかし、途中の各層における特徴量を変換する操作に上記で導入したように同変性を課すことで、物理的な対称性の情報をネットワークのより深いところに伝えることができます。
4.3 空間反転と時間反転
先ほど、同変性を導入する際に \(\text{O(3)} = \text{SO(3)}\times Z_2\) のように直交群を分解してSO(3)のみ既約表現を考えました。しかし、O(3)全体を考えるためには空間反転 \(I\) に対する \(Z_2\) インデックスの方も考慮しなければなりません。そのようなインデックスを \(p\) としたときに、\(p=+1\) であるものをparity (空間反転) even、\(p=-1\) であるものをparity oddと呼称します。
実際に \(\vec{r}_{ij}, \vec{m}_{i}\) に対する空間反転操作を考えます。\(\vec{r}_{ij}\) は極性ベクトルであり空間反転操作 (座標系を反転) を施した時にその成分にマイナス符号がつきます。つまり空間反転操作で符号を反転させるためparity oddです。その一方で、磁気モーメント \(\vec{m}_{i}\) は角運動量などと同じく軸性 (擬) ベクトルです。そのため、座標系を反転させてもその成分にマイナス符号はつきません。つまりparity evenです。空間反転操作 (Spatial Inversion, SI) に対する変換性を以下の図に示します。
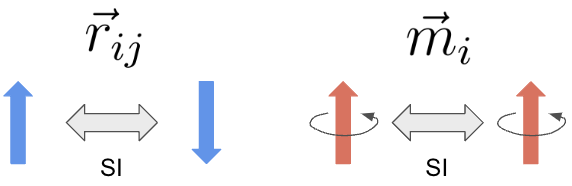
空間反転操作に対する変換性。
次に、時間反転操作 (Time Reversal, TR) に対する \(\vec{r}_{ij}, \vec{m}_{i}\) の変換性を考えます。時間反転操作についても空間反転パリティと同じように \(Z_2\) インデックスを導入すれば良いことがわかっています[8]。まず自明な例として、時間反転操作を施したとしても原子の位置やその相対ベクトル \(\vec{r}_{ij}\) は変化しないのでTR evenになります。その一方で、磁気モーメント \(\vec{m}_{i}\) は時間反転操作によって符号を反転させるためTR oddとなります。以下に時間反転操作による変換性を示します。
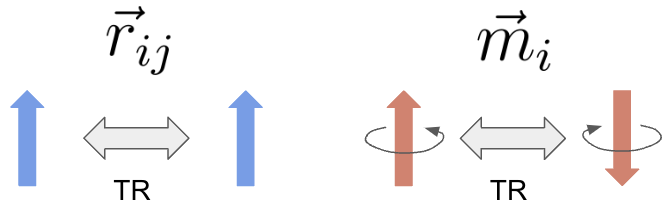
時間反転操作に対する変換性。
以後既約表現を記す際は、既約表現の自由度 \(\ell\) に加えてパリティ (eまたはo)、そして時間反転対称性 (EまたはO) を共に記すこととします。
4.4 既約表現のテンソル積
SO(3)既約表現に対する重要な演算として、二つの既約表現のテンソル積があります。二つの既約表現のテンソル積は、一般に既約とは限らず、以下のように再度既約表現の直和に分解されます。
$$
\ell_1\otimes\ell_2 = |\ell_1-\ell_2|\oplus\cdots\oplus(\ell_1+\ell_2)
$$
ここでは簡略化のために量子数 \(\ell\) に対応する線形空間も \(\ell\) と表記しています。また、それぞれ既約表現 \(\ell_1, \ell_2\) に属する特徴量 \(x^{\ell_1} ,y^{\ell_2}\) のテンソル積から既約表現 \(\ell_3\) に属する特徴量 \(z^{\ell_3}\) が生まれるとすると、その各成分はClebsch-Gordan係数 \(C_{\ell_1, m_1, l_2, m_2}^{\ell_3, m_3}\) を用いて以下のように紐付いています。
$$
\begin{align}
z_{m_3}^{\ell_3} &= x_{m_1}^{\ell_1} \otimes y_{m_2}^{\ell_2} \nonumber\\
&= \sum_{m_1, m_2} C_{\ell_1, m_1, l_2, m_2}^{\ell_3, m_3} x_{m_1}^{\ell_1} y_{m_2}^{\ell_2}.\nonumber
\end{align}
$$
この演算は、量子力学における角運動量の合成に対応しています。テンソル積は\(1\otimes{1}=0\oplus{1}\oplus{2}\)のように異なる既約表現の特徴量間を繋ぐため、同変性を担保しながらネットワークに表現力を持たせるために重要になります。
これに加えて、今回のケースでは前項で導入した空間反転と時間反転に関する \(Z_2\) インデックスも考慮しなければなりません。空間反転と時間反転に関するそれらのインデックスをそれぞれ \(p,\, t = \pm1\) とすると以下のような条件を満たす既約表現間のテンソル積しか許されません。
$$
p_3 = p_{1}p_2\\
t_3 = t_{1}t_2
$$
そのため、ネットワークアーキテクチャを考える上では既約表現 \(\ell\) の組み合わせのみならず、これら二つの \(Z_2\) インデックスの組み合わせを考慮して、取り入れたいテンソル積が層の途中で消えないようにすることが重要です。
4.5 ネットワークアーキテクチャ
これまでに導入した同変性などの道具を用いて、磁性NNPを構築することを考えます。
ネットワークのアーキテクチャを図に示します。アーキテクチャは[8]を参考にしており、コードは[9]で公開されているものを一部用いました。
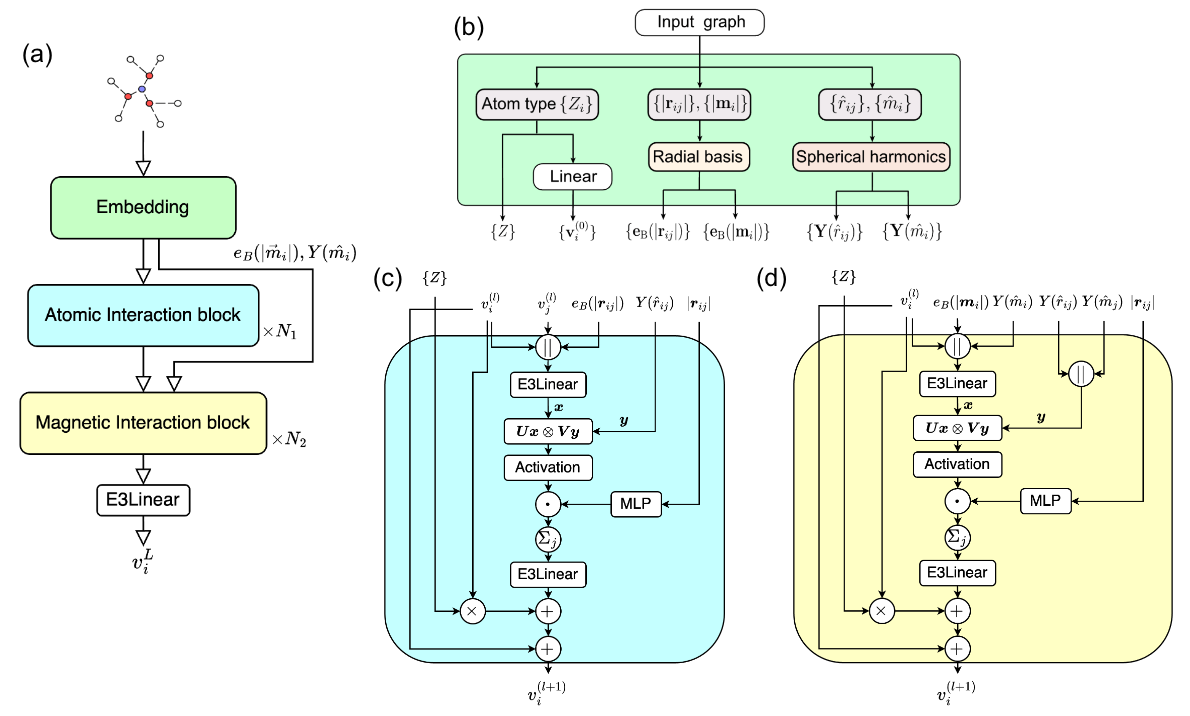
磁性NNPのアーキテクチャ図。(a)全体像。(b)Embedding block, (c)Atomic interaction block, (d)Magnetic interaction block。(b)は[8]より引用。
構造はグラフの形で入力され、まず初めにEmbedding blockによって特徴量に変換されます。その際、原子番号 \(\{Z_i\}\) はone hotベクトル及びその線形変換で、そして \(\vec{r}_{ij}, \vec{m}_i\) は大きさと方向をそれぞれガウス基底関数と球面調和関数を用いて変換されています。大きさの変換に用いたガウス基底関数\(\vec{e}_{\textrm{B}}\)は、次のように定義しています。
$$
\begin{align}
\left[\vec{e}_{\mathrm{B}}(|\vec{r}_{ij}|)\right]_n = \exp\left( -\frac{\left( |\vec{r}_{ij}| – r_n \right)^2}{2 \Delta^2} \right) \tag{**}
\end{align}
$$
ここで、どれだけ離れたエッジまでとるかのカットオフ半径を \(r_{\textrm{cut}}\)、そして基底関数の数を \(N_r\) とすると \(\Delta=r_{\textrm{cut}}/N_r, \ \ r_n = n\Delta\) として定義される量を用いています。
続けて、Atomic interaction blockを複数層作用させることで原子構造を特徴付け、続けて複数層のMagnetic interaction blockによってスピン構造を特徴づけています。ネットワーク全体を通して、中間層ではnodeの特徴量 \({v_{i}}\) のみを更新しています。最終層の出力 \(\tilde{v}_i\) は各node (原子) \(i\)に対して \(\ell=0,p=1,t=1\) に対応するスカラーで与えられ、それぞれの構造でnodeに関して総和をとることでエネルギーを計算します。
$$
E = \sum_{i}\tilde{v}_i
$$
Atomic interaction blockについては[8]と同じアーキテクチャを用いていますが、Magnetic interaction blockについては変更を加えています。具体的には、磁気モーメントの球面調和関数 \(Y^{\ell}(\hat{m}_i)\) について、異なるnode間 \((i,j)\) のテンソル積を陽にネットワークに組み込みました。
テンソル積の一部は \(Y^{\ell_1}(\hat{m}_i)\otimes(Y^{\ell_2}(\hat{r}_{ij})\oplus{Y}^{\ell_3}(\hat{m}_{j}))\) の形になっており、各層で明示的に”node \(i\) の磁気モーメント \(\vec{m}_i\) と、 \(\vec{r}_{ij}\) 方向に離れたnode \(j\) における磁気モーメント \(\vec{m}_j\) 間の相互作用”を取り入れたことに対応します。また、このテンソル積によってTR oddの表現同士のテンソル積からTR evenなスカラー量が生まれ、最終層のアウトプットであるエネルギーに対する寄与が生まれます。
図中にある他の操作は以下のような操作とします。
| 演算名 | 内容 |
|---|---|
| e3Linear | 同じ既約表現内で線形変換を施す。定義は[8]等参照。 |
|
\(\boldsymbol{Ux}\otimes\boldsymbol{Vy}\)
|
入力ベクトル\(\boldsymbol{x}, \boldsymbol{y}\)に対する学習可能パラメータである線形変換の重み\(\boldsymbol{U,V}\)付きのテンソル積。
|
| Activation |
同変性を保ちつつ非線形関数\(\eta\)を作用させる。\(\eta\)としてはSiLU関数を使用。定義は[10]参照。
|
| \(\odot\) | 二つの入力ベクトルについて要素ごとの単純な積算 (アダマール積)。 |
|
\(\sum_j\)
|
node(\(i\))に隣接するnode(\(j\))に関する総和。
|
|
\(\times\)
|
Fully connected tensor productと呼ばれる重み付きテンソル積。定義は[10]参照。 |
| 要素ごとの単純な和算。同じ既約表現で多重度が異なる場合にはe3Linearを作用させる。 | |
| MLP |
edgeの長さを特徴付ける3層の全結合Multi Layer Perceptron。
edgeの長さ \({r}_{ij}\) は、式(**)で定義したガウス基底関数で展開したものに多項式のenvelope関数[11]をかけたものになっている。
|
4.6 スピン模型データセットによる学習結果
3節で紹介した、SDFTではなくスピン模型を用いて作成したデータセットに対して、このモデルを適用していきます。データセット全体を8:2の比率でtrainデータとvalidationデータに分割し、Loss function \(L\) の形は以下のように設定しました。
$$
L = \lambda_E \|\hat{E} – E\|^2 + \frac{\lambda_F}{3N} \sum_{i=1}^{N} \sum_{\alpha=1}^{3} \left\| \frac{\partial \hat{E}}{\partial r_{i,\alpha}} – F_{i,\alpha} \right\|^2 + \frac{\lambda_{F_{\text{mag}}}}{3N_{\text{mag}}} \sum_{j=1}^{N_{\text{mag}}} \sum_{\beta=1}^{3} \left\| \frac{\partial \hat{E}}{\partial m_{j,\beta}} – F_{\text{mag},j,\beta} \right\|^2,
$$
ここで、\(\lambda_{E}, \lambda_{F}\) および \(\lambda_{F_{\textrm{mag}}}\) は、それぞれ全エネルギー、force、magnetic forceの重みを表します。\(N\) は原子数を表し、\(\alpha, \beta\) は座標の添字です。また、\(\hat{E}\) がNNPの出力であり、\(E, F, F_{\text{mag}}\)がそれぞれ教師データの値であるとします。
学習の際、各種インプットのパラメータは以下のように設定しました。
| パラメータ名 | 設定値 |
|---|---|
| カットオフ半径 | 5 Å |
| \({r_{ij}}, {m_{i}}\)のガウス関数展開における基底数 | 16 |
| MLPの中間層におけるperceptronの数 | 64 |
| \(\vec{r_{ij}}, \vec{m_{i}}\)に対する球面調和関数の最大角量子数 | 1 |
| Atomic interaction blockの数 | 4 |
| Atomic interaction blockの出力既約表現 | 16x0e + 8x1o |
| Magnetic interaction blockの数 | 3 |
| Magnetic interaction blockの出力既約表現 | 16x0eE + 8x1oE + 16x0eO + 8x1oO |
| 最終層の出力(エネルギー) | 0eE |
| \(\lambda_{E}, \lambda_{F}, \lambda_{F_{\textrm{mag}}}\) | \(10^2, 10^3, 10^5\) |
学習したモデルをvalidationデータセットに適用した結果を以下に示します。energyとforceに加えて、磁気モーメントに対するmagnetic forceもきちんと学習できていることがわかります。また、単位原子あたりのenergyに対するMAEは約 0.007 eVと、3.2で調べたスピン構造によるエネルギー変化のスケール \(\sim 0.1\) eV に対して十分小さく、よく学習できていることが分かります。
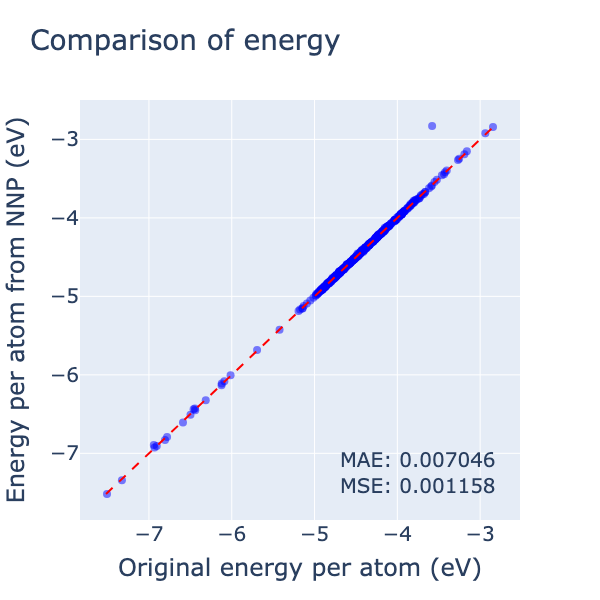
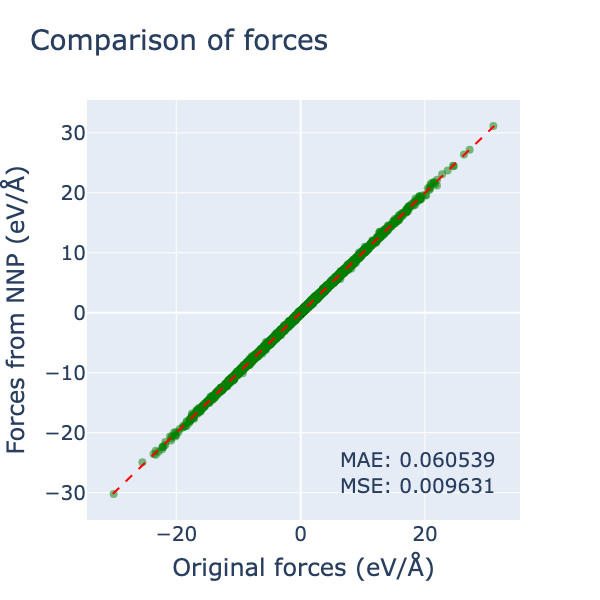
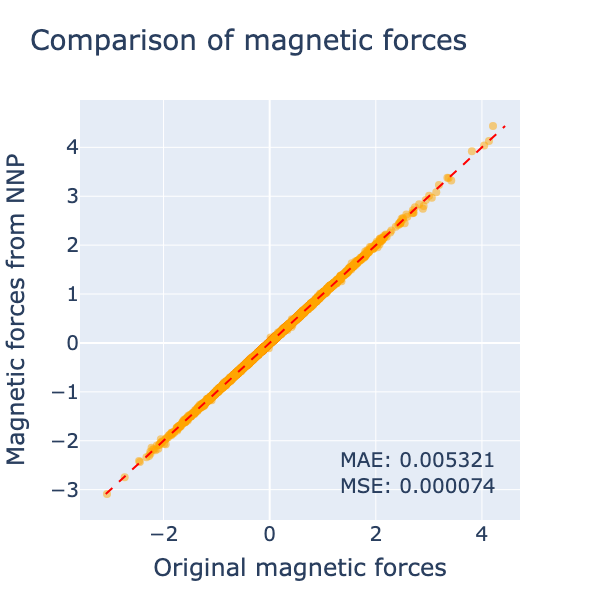
今回は3節で導入したスピン模型によるデータセットを学習したため、cDFTを用いた場合に起こりうるmagnetic forceがエネルギーの微分と不整合になるといった問題は起きません。しかし、2節で作成したようなcDFTを用いたデータセットに対しては、2.3で言及したようにmagnetic forceの影響で学習が妨げられる可能性があります。今回はそこまで取り組むことはできませんでしたが、検証したい重要な問題だと考えています。
5. 終わりに・謝辞
本インターンシップでは、スピン構造の自由度も取り込んだNNPの開発に取り組みました。また、本テーマでは例外的に二人で一つのテーマに取り組む形式を取らせていただき、内容はデータセットの作成からNNPの実装、さらにはダイナミクスシミュレータの実装まで、多岐にわたるものとなりました。7週間という短い期間でさまざまな課題に取り組むことができ、大変充実した経験となりました。
結果的に実装したアーキテクチャを実際の物質で試すまでには至りませんでしたが、スピン模型で作成したデータセットでは良好な学習結果が得られました。また、二人で一つのテーマに取り組んだことで、それぞれの専門分野に関連する知見を共有する機会も多く、非常に実りあるインターンシップとなりました。
メンターの倉田さん、宮崎さんをはじめ、PFNの社員の方々には、日々のディスカッションや中間・最終発表での議論、そして気さくな雑談まで大変お世話になりました。PyTorchを用いたNeural Networkや、原子とスピンの自由度を組み合わせたダイナミクスシミュレーションの実装経験が浅く、さらにe3nn[10]の既約表現やテンソル積などに苦戦することもありましたが、その都度デバッグ方針などをご指導いただき、無事に本ブログとしてまとめることができました。
普段の研究とは異なる分野での経験を通じて、社員の方々や他のインターンシップ参加者との交流が多くの刺激となり、非常に楽しい時間を過ごすことができました。最後になりますが、本インターンシップの運営に携わってくださった皆様に、心より感謝申し上げます。ありがとうございました。
Reference
[1] https://physics.aps.org/articles/v8/s130
[10] Geiger, Mario, and Tess Smidt. “e3nn: Euclidean Neural Networks.”, arXiv:2207.09453 (2022)




