Blog
吉田です。今まで数解に渡って乱択アルゴリズムを紹介してきました。そろそろ解析やアイデアがシンプルかつ結果が綺麗な乱択アルゴリズムは尽きてきたかと思っていましたが、もう一つとても素敵な手法が有るのを思い出しましたので解説します。Color Codingと呼ばれる手法です。
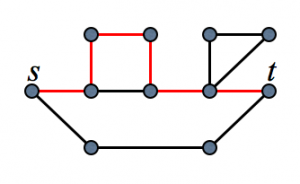
\(G = (V, E)\)をグラフ、\(s,t\in V\)を\(G\)中の二頂点、\(k\geq 0\)を整数とします。\((s,v,k)\)パスとは、\(s\)と\(t\)を結ぶパスで内点の個数が丁度\(k\)個のものを指します。但しパスは同じ頂点や枝を二度使ってはいけません。例えば以下の図で赤い線で示されているパスは\((s,t,5)\)パスです。
さて次で定義される\((s,t,k)\)パス問題を考えましょう。
入力: グラフ\(G=(V,E), s,t \in V, k \geq 0\)
出力: \((s,t,k)\)パスが存在するか?
この問題は、自明に\(O(n^{k})\)時間で解けます(\(n\)はグラフの頂点数)。即ち、\(s\)から深さ優先探索を用いて、\(k\)個の点を経由して\(t\)に行けるかを調べれば良いです。
しかし、この計算時間は\(n\)の肩に\(k\)が乗っているのが気になります。この肩の\(k\)を外すことは出来ないでしょうか?つまり、ある関数\(f\)と定数\(c\)に対して、\(O(f(k)n^c)\)時間で\((s,t,k)\)パスを見つけることは出来ないでしょうか?
これを実現するのに使うのがColor Codingと呼ばれる手法です。
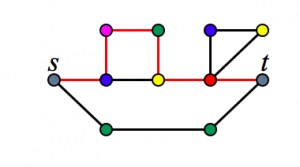
まず準備として、\(k\)色を用いて頂点に色を塗った色つきグラフ\(G=(V,E,\beta)\)を考えます。ここで\(\beta: V \to \{1,\ldots,k\}\)が頂点の色に対応しています。色つきグラフにおいてカラフル\((s,t,k)\)パスとは、\(s\)と\(t\)を結ぶパスで、内点の個数が丁度\(k\)個かつ内点で全ての色を一度ずつ使うもののことを言います。例えば、以下の図で赤い線で示されているパスはカラフル\((s,t,5)\)パスとなっています。
次で定義されるカラフル\((s,t,k)\)パス問題を考えましょう。
入力: 色つきグラフ\(G=(V,E,\beta), s,t \in V, k \geq 0\)。
出力: カラフル\((s,t,k)\)パスは存在するか?
もしカラフル\((s,t,k)\)パス問題が\(T(n,k)\)時間で解けるとすると、\((s,t,k)\)パスもないは次のようにして(確率的に)解くことが出来ます。
- \(k\)色を用いて頂点にランダムに色を塗り、得られた色つきグラフを\(G’=(V,E,\beta)\)と置く。
- もし色つきグラフ\(G=(V,E,\beta)\)がカラフル\((s,t,k)\)パスを持てばYesと出力、持たなければNoと出力。
上のアルゴリズムの計算量は明らかに\(T(n,k)\)です。もし\(G\)が\((s,t,k)\)パスを持つとしましょう。すると\(G’\)がカラフル\((s,t,k)\)パスを持つ確率は少なくとも\(\frac{k!}{k^k} > e^{-k}\)です。よって少なくとも\(e^{-k}\)以上の確率でYesと出力します。もし\(G\)が\((s,t,k)\)パスを持たないとしましょう。すると\(G’\)はカラフル\((s,t,k)\)パスを持たないので、確率1でNoと出力します。
後はいつものように上のアルゴリズムを\(e^k\)回繰り返し、一度でもYesと出力すればYes、そうでなければNoと出力します。そうすると計算時間\(T(n,k)e^k\)で、\((s,t,k)\)パスを持つときに確率\(2/3\)以上でYesと出力し、そうでないとき確率\(1\)でNoと出力するアルゴリズムが得られます。
カラフル\((s,t,k)\)パス問題は簡単な動的計画法で解くことができます。まず\(v \in V, C \subseteq \{1,\ldots,k\}\)に対して、\(x[v, C]\)は\(s\)から\(v\)へ\(C\)中の色を丁度一度ずつ使うパスがあるかを表すとします。すると明らかに\(x[v,\emptyset] = \mathrm{true}\)です。また\(v\)の色が\(r \in \{1,\ldots,k\}\)の時、\(x[v, C] = \bigcup _{(u,v) \in E}x[u, C \setminus \{r\}]\)と計算できます。
さてカラフル\((s,t,k)\)パスが存在することと、ある\(t\)の隣接頂点\(v\)が存在して\(x[v, {1,\ldots,k}] = \mathrm{true}\)であることは同値なので、\(x[v,C]\)を全ての\(v\)と\(C\)に対して求めてあげればカラフル\((s,t,k)\)パス問題が解けたことになります。\(x[v,C]\)の状態数は\(O(n2^k)\)で、一つの値を計算するのに\(O(n)\)時間かかるので、全体で\(O(n^2 2^k)\)時間で計算できます。よって\(T(n,k)=O(n^22^k)\)となります。
先ほどの議論と合わせると、\((s,t,k)\)パス問題を\(T(n,k)e^k = O(n^22^ke^k) = O((2e)^k n^2)\)で解くことが出来ることが分かります。
さて今回の\((s,t,k)\)パス問題では\(O(f(k)n^c)\)時間で解くことが出来ました。\(k\)というパラメータが入力の一部である問題が、\(O(f(k)n^c)\)時間で解けるとき、その問題をFixed Parameter Tractable (FPT)と呼びます。FPTを研究するモチベーションはやはりNP困難な問題をあるパラメータが小さい時に速く解きたいというところから来ていると思います。既にFPTは理論計算機科学の中で確立した分野として扱われていて、専用のワークショップも開催されている程です。
Color Codingの応用は勿論パスを見つけることだけでは有りません。自明な拡張としては、その木など他のグラフを部分グラフとして含むかという問題を解くのに利用できます。また非自明な応用としては、最大\(k\)頂点被覆問題の近似を行うのに利用できます。最大\(k\)頂点被覆問題は、グラフから\(k\)個の頂点を選び、それらの頂点に隣接する枝の総数を最大化するという問題です。
Tag