Blog
本記事は2025年度PFN夏期インターンシップで、拡散モデルを用いた結晶構造生成手法に取り組まれた石井孝憲さんによる寄稿です。
はじめに
2025年度の夏季インターンシップ に参加させていただきました、東京科学大学 物質理工学院 材料系 D2の石井孝憲です。普段は第一原理計算を用いた固溶体中の点欠陥の研究をしています。今回の夏季インターンでは、対称性を考慮した拡散モデルによる結晶構造の条件付け生成に関する研究に取り組みました。
背景
材料探索において結晶構造予測(CSP:Crystal Structure Prediction)は上流の合成計画と実験合成を支える基本的かつ重要なタスクです。実験的に未知の結晶を探索する際に、理論計算を用いたアプローチが重要となってきています。
CSPは安定な結晶構造を予測する上で重要な役割を果たすものの、結晶構造の様々な多形や組成を考慮するとその組み合わせとなる探索空間は膨大となり、効率よく探索するには計算手法の開発が不可欠です。新規結晶構造生成のアルゴリズムには一般的にメタヒューリスティックアルゴリズムが用いられ、ランダム構造探索(Random Structure Search)、遺伝的アルゴリズム(GA: Genetic Algorithm)、ベイズ最適化などが挙げられます。
近年では、それらとは異なるアプローチとして、変分オートエンコーダー(VAE: Variational Autoencoder)や拡散モデルを用いた新規結晶構造生成モデルの研究[1][2]も盛んに行われています。中でも、MatterGen[3]は条件付き生成が可能なモデルとして提案され注目を集めていました。その一方で、MatterGenは学習データに含まれる構造よりも対称性の低い構造を生成する傾向があります。対称性を厳密に指定可能なアプローチとして、対称性を明示的に符号化することで、生成モデルがより高対称性を持つ興味深い物質空間内に限定して生成できるようにするWyckoffDiffなども提案されています。
その中でも本研究ではMicrosoftが提案した結晶構造拡散モデルであるMatterGenに着目し、改めてMatterGenでの結晶構造生成の限界を調査しました。そして生成する結晶構造の対称性の低下を解消するようなモデルであるWyckoffDiff [4]をベースとして、高対称性を持つ構造を条件付け生成できるようにし、それによる性能検証を行いました。
手法
MatterGenでの結晶構造生成
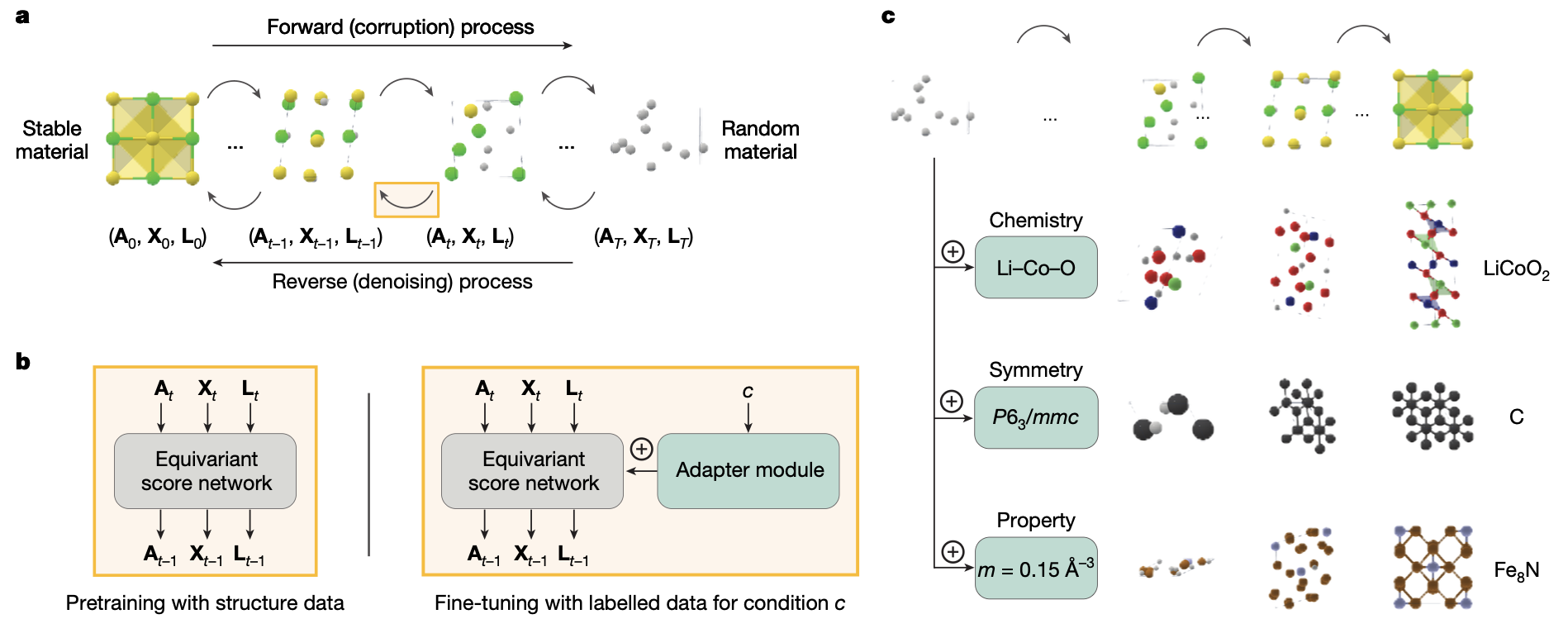
図1: MatterGenの概要図より
MatterGenは元素(離散)×座標(連続)×格子(連続)を同時に拡散して結晶構造を生成する拡散モデルです。MatterGenでは結晶構造は以下で表現される\(\boldsymbol{M}\)で表されます。
$$\boldsymbol{M} = ({ \boldsymbol{A}, \boldsymbol{X}, \boldsymbol{L} }) $$
ここで \(\boldsymbol{A} = (a^1, a^2, \ldots, a^n)^\top \in \mathbb{A}^n\)はセル内の原子種、\(\boldsymbol{X} = (\boldsymbol{x}^1, \boldsymbol{x}^2, \ldots, \boldsymbol{x}^n) \in [0,1]^{3 \times n}\) は原子座標、\(\boldsymbol{L} = ( \boldsymbol{l}^1, \boldsymbol{l}^2, \boldsymbol{l}^3 ) \in \mathbb{R}^{3 \times 3}\)は格子ベクトルに対応しています。
MatterGenでは、
- 原子種は離散拡散(D3PM[5])
- 原子座標と格子は連続拡散
でモデルを学習することにより、結晶構造を生成しています。
ここでもう1つMatterGenの特徴としてあげられるのはAdapter moduleの追加による物性値を入力とした条件付け生成です。Adapter moduleは各メッセージパッシング層の直前に置き、第\(L\)層目の物性情報を付加後の隠れ層\(\mathbf{H}_j^{\prime (L)}~\)は以下の式で与えられます。
$$\mathbf{H}_j^{\prime (L)} = \mathbf{H}_j^{(L)} + f_{_\text{mixin}}^{(L)} \left( f_{_\text{adapter}}^{(L)}~(\mathbf{g}) \right) \cdot \mathbb{I}_{({\text{property is not null}})}$$
ここで、\( f_{_\text{mixin}}^{(L)}~\)はバイアスなしのゼロで初期化された線形層、\(f_{_\text{adapter}}^{(L)}~\) は2層のMLPに対応しています。最後のインジケータ関数によって、条件ラベルが与えられない場合はモデルが無条件スコアを出力するようになっています。
WyckoffDiffモデルを用いた結晶構造生成
WyckoffDiffのコンセプトとしては、対称性を先に確定し、その上で原子を配置することで、従来の結晶生成モデルで直面していた対称性の低い空間群(=P1)に偏りがちとなる問題を解決するというものです。
WyckoffDiffは以下の図2に示すような結晶の対称性(空間群+Wyckoff位置)をそのまま入力にした離散拡散モデルです。図2のようにワイコフ位置をノードとする完全グラフにメッセージパッシングを行い、各変数のカテゴリ分布を出力します。対称性を明示的に入力にし、出力をprotostructure(=元素×Wyckoff位置の占有情報)を生成するため、MatterGenのような座標を生成するような生成モデルとは異なり、生成した構造の対称性を保証するものとなっています。
WyckoffDiffでは結晶構造はprotostructureとして以下で定義されます。
$$\boldsymbol{M} = (s, \boldsymbol{z}^\infty, \boldsymbol{z}^0)$$
ここで、\(s\)は空間群、\(\boldsymbol{z}^0\)は座標\(({x, y, z})\)の全てに何らかの制限がついている位置である制限付きワイコフ位置(constraint position)、\(\boldsymbol{z}^\infty \)はそれ以外のワイコフ位置である自由度付きワイコフ位置(unconstraint position)と定義しています。(一般的に結晶学では、席対称群が恒等操作しか含まないワイコフ位置を一般位置(general Wyckoff position)、それ以外のものを特殊位置(special Wyckoff position)といいます。)
ここでWyckoffDiffは
- 自由度付きワイコフ位置では原子種\( \times\) 個数の行列 \(\boldsymbol{z}^\infty \)
- 制限付きワイコフ位置では原子種+0(空席)のベクトル\( \boldsymbol{z}^0 \)
をそれぞれ離散拡散で逆生成することによりモデルを学習し、結晶構造を生成しています。

図2: WyckoffDiffの概要図[4]より引用
元のWyckoffDiffの実装では物性値による条件付け生成をすることができません。そこでMatterGenが採用しているAdapter moduleによる物性値での条件付け生成を可能にするために、Adapter moduleをWyckoffDiff側に実装しました。
追加されるAdapter module付きWyckoffDiffのアーキテクチャの全体図を図3に示します。
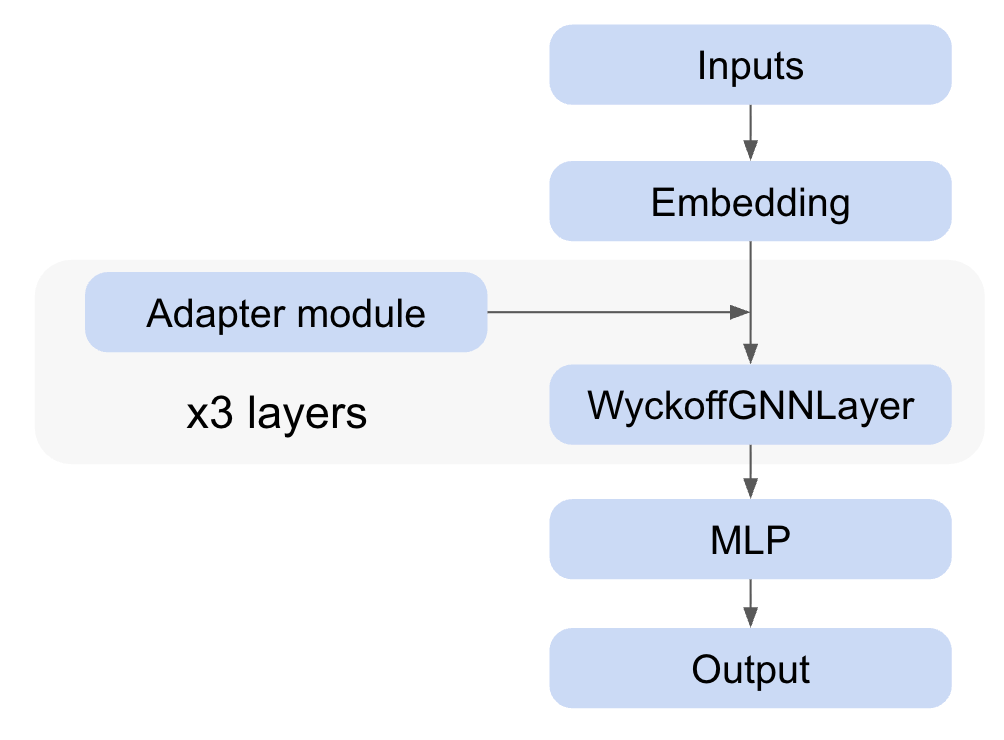
図3: Adapter module付きWyckoffDiffのアーキテクチャの全体図
計算条件
生成した結晶構造をMatterSim[6]を用いて構造最適化して構造安定性を評価します。また、datasetにはMatterGenとWyckoffDiffにも使われていたMP-20 datasetを用いて学習を行います。

図4: 各原子種の学習用dataset内での登場回数を示した周期表(pymatviz[7]を用いて描画)
一例として各原子種の学習用dataset内での登場回数を図4に示します。datasetはunit cell内の原子数が1~ 20となるような系が入っていて、全体として酸化物が多い傾向があります。
結果
ここでは、MatterGenとWyckoffDiffでそれぞれ空間群とenergy above hull、原子種の3つを指定した条件付け生成を行い、安定な構造が生成できているかの比較を行います。また、構造最適化を行った後の対称性が指定した空間群の属する結晶系にどれだけ収まっているかをヒートマップでプロットし評価します。最後に、MatterGenとWyckoffDiffの結晶構造の生成速度の比較結果を示します。
MatterGenでの条件付け生成
MatteGenでAdapter moduleを用いて空間群、energy above hull、原子種を指定して条件付け生成できるようにした結果が以下になります。
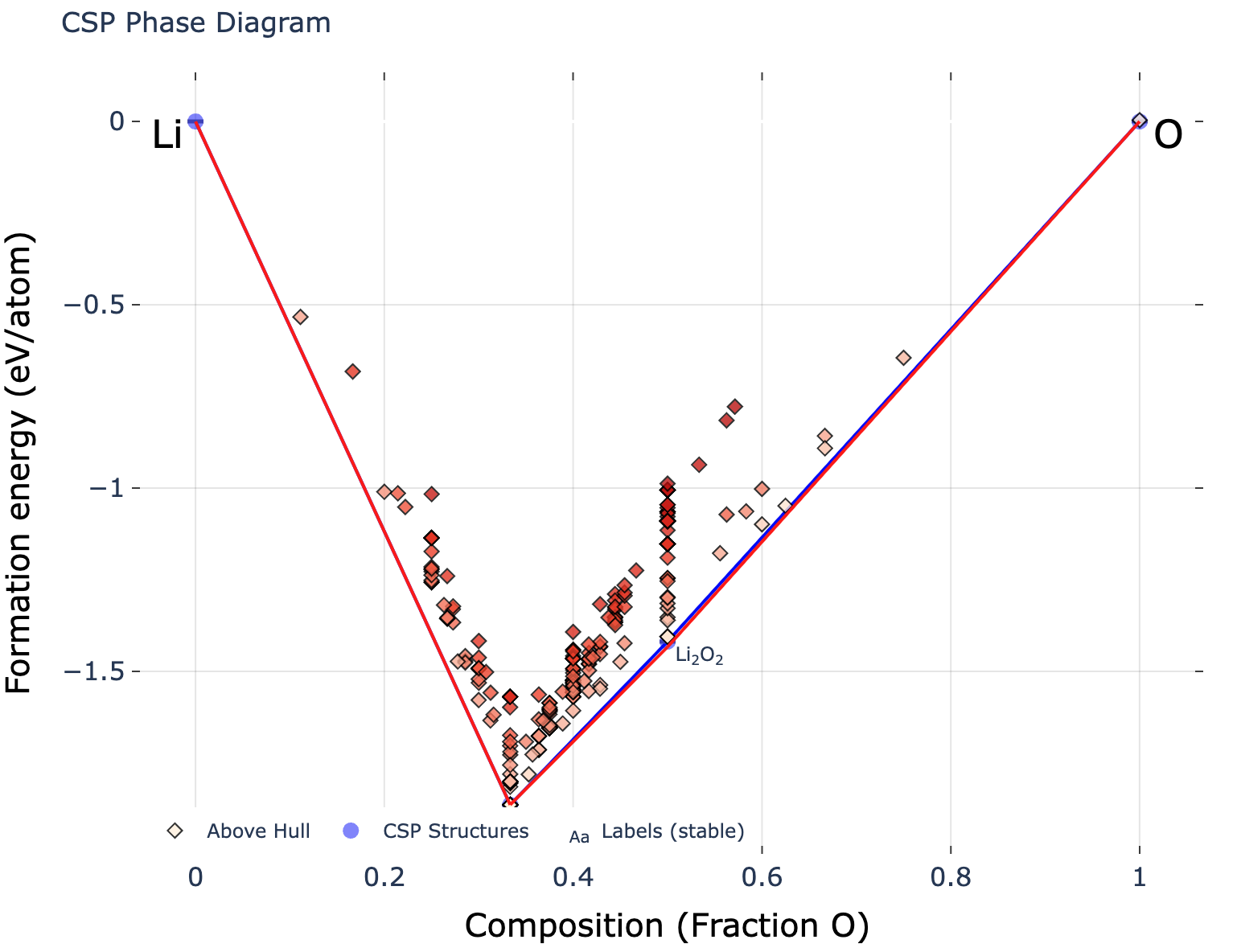
図5.1.1: MatterGenで条件付け生成したLi-O系のPhase Diagram
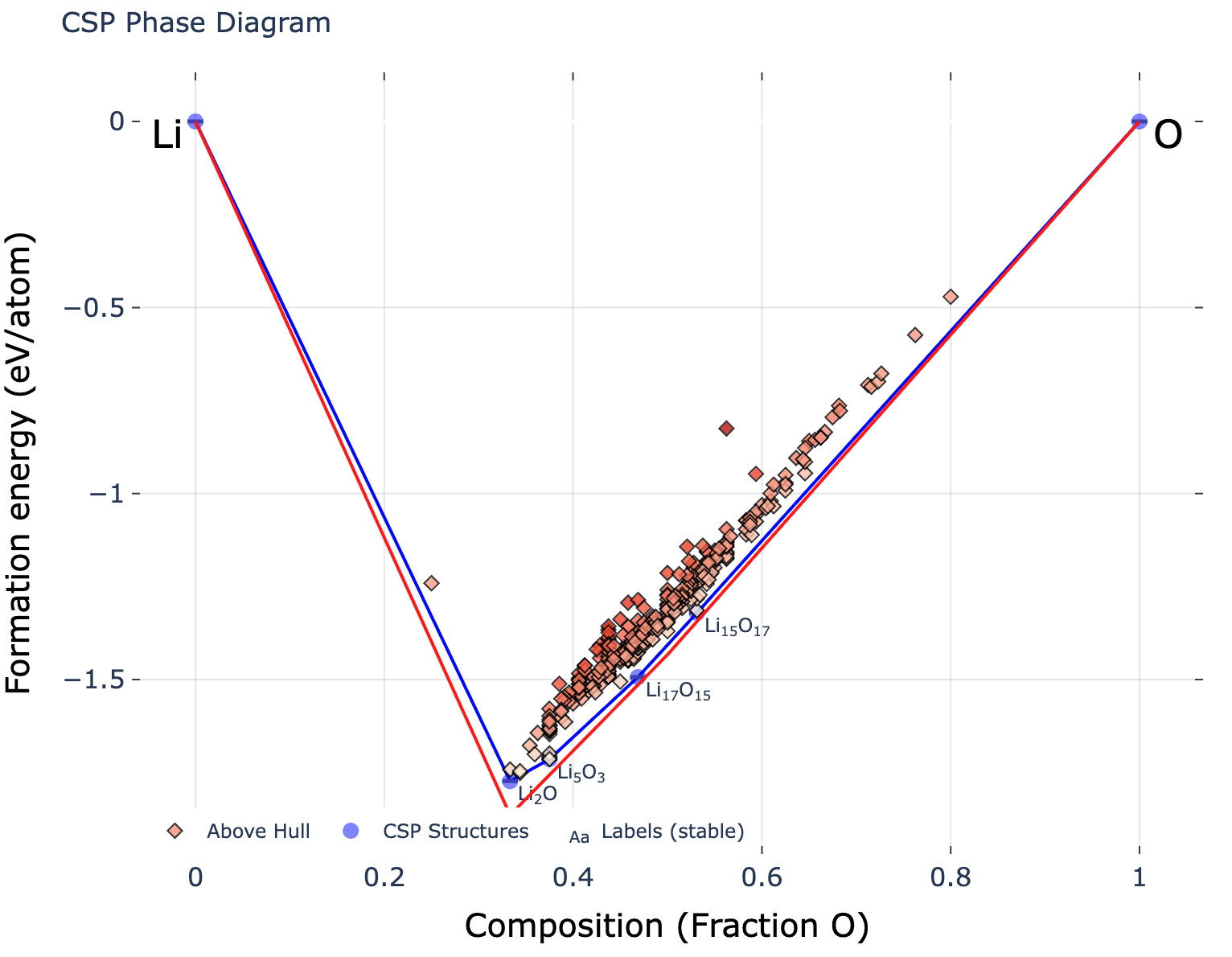
図5.1.2: サンプリングする原子数を8倍してMatterGenで条件付け生成したLi-O系のPhase Diagram
Adapter moduleでenergy above hull = 0、系をLi-O系、空間群に関してはデータセットを空間群で分類したときに頻出の上位20個の空間群をそれぞれ指定してLi-O系のPhase Diagramをプロットしたものが図5.1.1、5.1.2になります。赤色はMaterials Project[8][9]内にある安定構造、青色はMatterGenで生成した安定構造を結んだhullとなっています。各ひし形の点は生成モデルにて生成した系1つ1つに対応しています。
図5.1.1は図5.1.2に比べると、赤色の線と青色の線が重なっており、Materials Project内にあるような安定構造がよく生成できていると言えます。また、MatterGenによる結晶構造の生成傾向としては、サンプリングする原子数を元の系より大きくすると(今回はデータセットの分布に従う原子数の分布から原子数をサンプリングした値を8倍にし、その原子数に基づいて結晶構造を生成)生成される系の組成空間が限定される傾向があります。図5.1.2において横軸の酸素の組成比が0.5近傍に集まっていることから、外挿領域である学習データより巨大な系の生成ではランダムな系に近づくことが示唆されます。
MatterSimで構造最適化した後の空間群と結晶系のヒートマップをプロットしたものが以下になります。
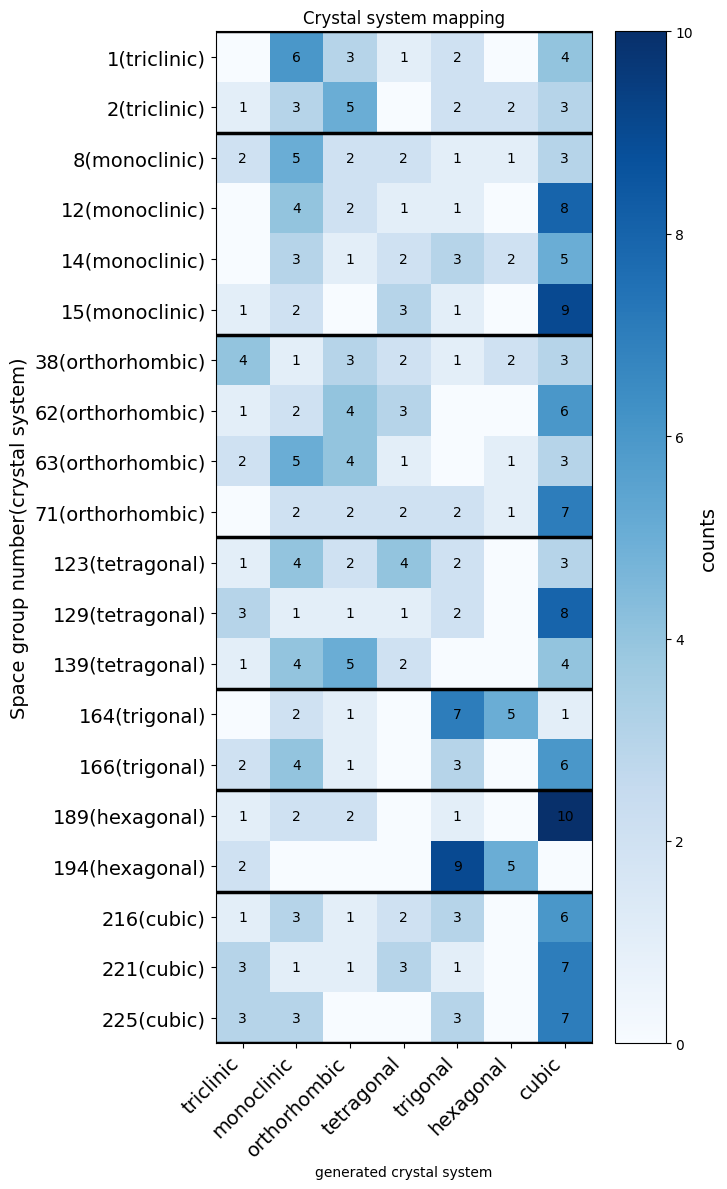
図5.1.3: (左)MatterGenで条件付け生成したときに指定した空間群とMatterSimを用いて構造最適化後のその結晶系のヒートマップ、 (右)サンプリングする原子数を8倍してMatterGenで条件付け生成したときに指定した空間群とMatterSimを用いて構造最適化後のその結晶系のヒートマップ
MatterGenで条件付け生成したときに指定した空間群とMatterSimを用いて構造最適化後のその結晶系のヒートマップを図5.1.3に示します。この図は縦軸が条件付け生成したときに指定した空間群で、横軸がMatterSimを用いて構造最適化後のその構造の結晶系に対応しています。ヒートマップの対角成分の色が濃い方が構造最適化後も指定した空間群の属するような結晶系が保たれていて良い結果となっています。
左の図から三方晶系(trigonal)や単斜晶系(monoclinic)ではやや構造最適化後も指定した空間群が属するような結晶系を保つような構造が生成されていますが、全体的に俯瞰してみるとそもそも指定した空間群が生成されていない、もしくはMatterSimで構造最適化をすると指定した空間群が分類されないような結晶系になるように構造最適化がされています。すなわち、MatterGenを用いて結晶構造生成を行うときに対称性をコントロールすることは難しいということが示唆されます。これが右図のサンプリングする原子数を8倍にした場合だとより顕著になり、空間群を指定したにもかかわらず、ほとんどの生成された結晶構造の対称性が低下して空間群がP1(No. 1)になってしまいます。
このようにMatterGenはAdapter moduleを用いた空間群の条件付け生成を行っても、対称性を保つような結晶構造生成の困難さがあることが示唆されます。そこでより対称性の制御性能を上げるために、今回は明示的にワイコフ位置のような対称性の情報を入力として扱う前述したWyckoffDiffを用いてMatterGenと性能の比較を行います。
WyckoffDiffでの条件付け生成
MatterGenと同様の条件でWyckoffDiffを用いてLi-O系の結晶構造の条件付け生成を行いPhase Diagramを描画した結果が図5.2.1です。
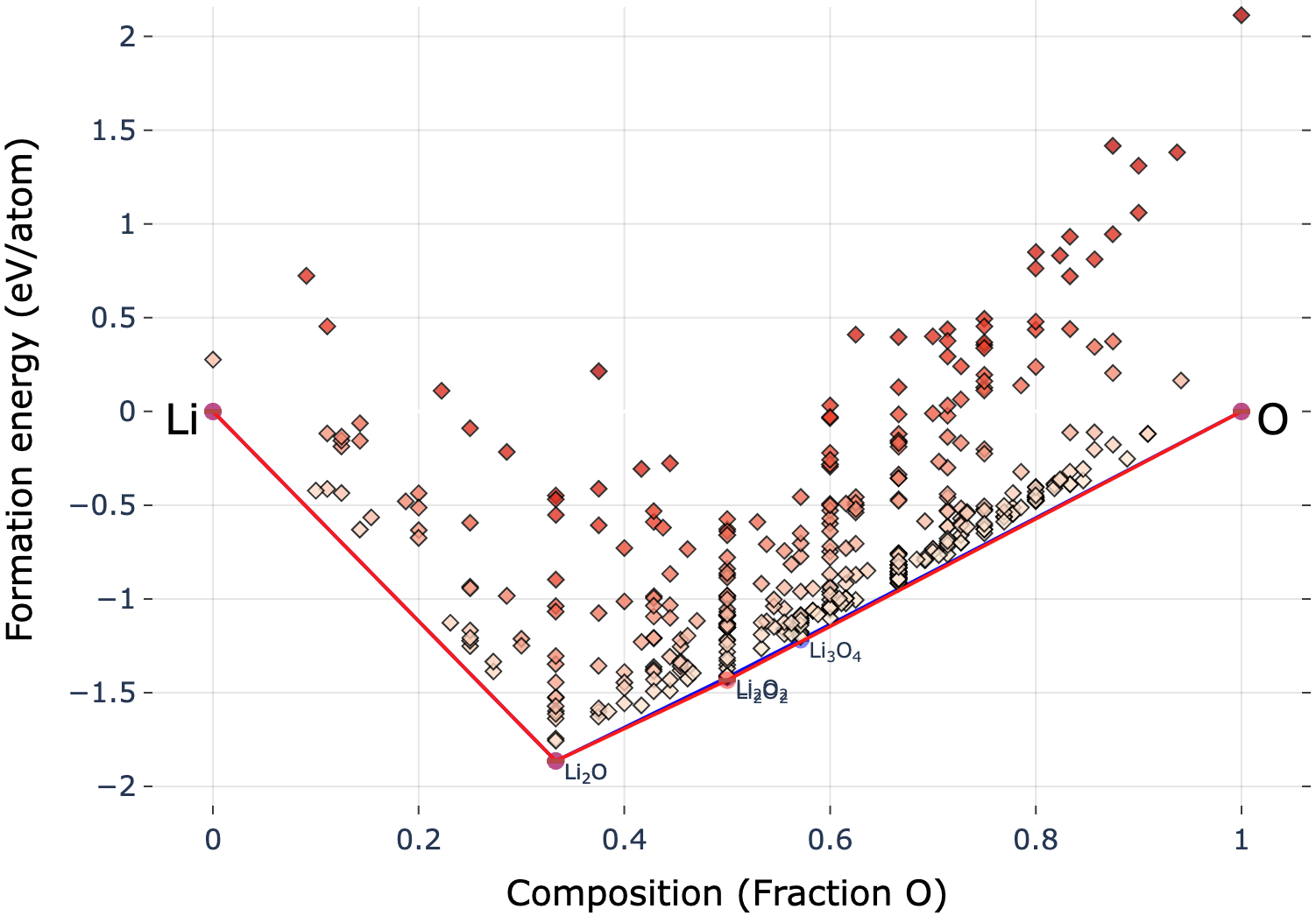
図5.2.1: Adapter module付きWyckoffDiffで生成したLi-O系のPhase Diagram
こちらの図も先程と同様に赤線はMaterials Project内にある安定構造を結んだhull、青線はWyckoffDiffで生成した安定構造を結んだhullとなっています。WyckoffDiffも赤線と青線がほとんど重なっていて、Li-O系の安定構造がよく探索できていることがわかります。そして構造最適化後も指定した空間群が属する結晶系がどれだけ生成されているのかを表す図が以下の図5.2.2です。MatterGenと比較すると対角成分の色が濃い、すなわち条件付け生成で空間群を指定して結晶構造を生成してその後構造最適化を行っても指定した空間群が属する結晶系を保っているということがわかります。
このように、WyckoffDiffはMatterGenよりも指定した対称性を保ちながら条件付け生成できていることが言えます。
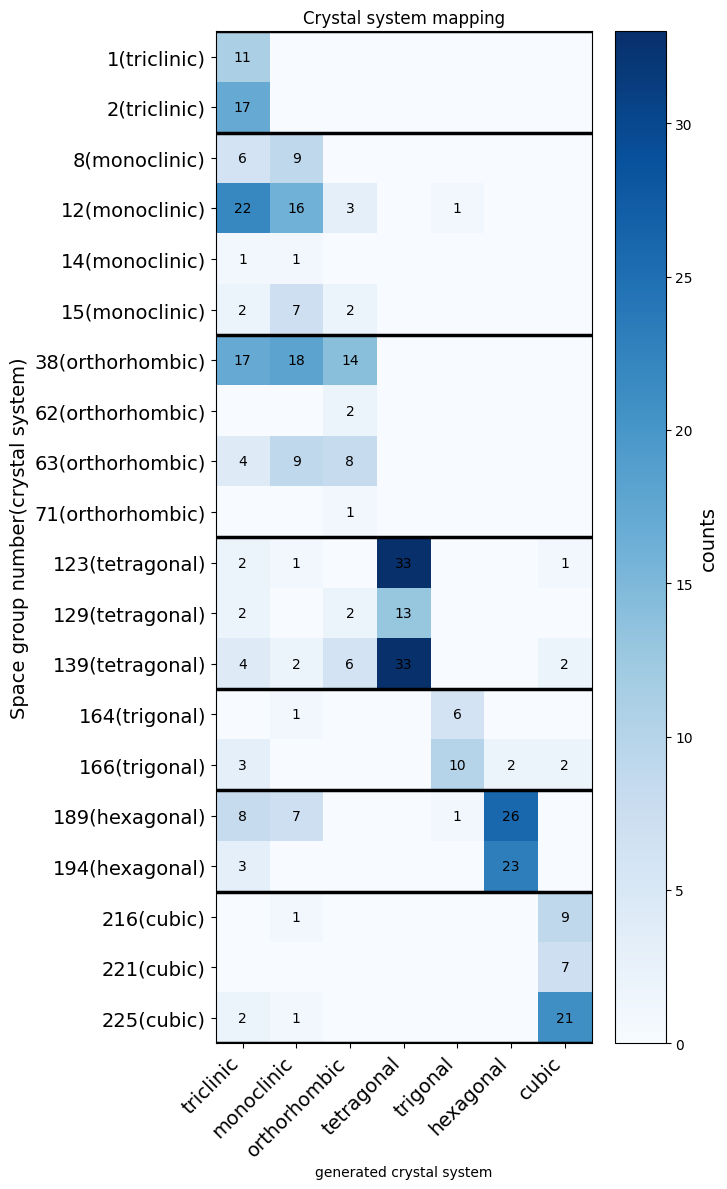
図5.2.2: WyckoffDiffで条件付け生成したときに指定した空間群とMatterSimを用いて構造最適化後のその結晶系のヒートマップ
計算速度の比較
ここではMatterGenとWyckoffDiffのcifファイルの生成までの時間を計測し下の表1に示します。
表1: MatterGenとWyckoffDiffのcifファイルの生成時間比較
| MatterGen | WyckoffDiff | |
| 生成速度(s) | 366 | 60(34(prototype) + 26(structure)) |
ベンチマークとして、表1はLi-O系の16サンプルのデータをV100(16GB)のGPUを用いて条件付け生成を行ったものです。MatterGenはcifファイルの生成に366秒かかるのに対し、WyckoffDiffはprototypeの生成とprototypeからcifファイルへの変換にそれぞれ34秒と26秒と合計で60秒程度とMatterGenのおよそ6倍程度早くcifファイルを生成できることがわかります。
考察
WyckoffDiffの課題点
一方でWyckoffDiffを用いた結晶構造の課題点も存在します。以下が空間群が \(Fm\overline{3}m\) (No. 225)、energy above hull = 0、Ba-Ta-In-O系で条件付け生成を試みた生成結果の一部が図6.1になります。本来期待していた構造としては学習データセットのMP-20には存在しないが、Materials Projectには存在する図6.2のような構造です。しかし、生成された構造は図6.1に示した構造のようになり、対称性そのものはあっても、化学結合・配位数的におかしな構造が生成されることがわかります。このような化学結合的に無理のある構造が生成された結果、MatterSimで構造最適化をしてPhase Diagramを描画したときにMatterGenと比較してWyckoffDiffの方がenergy above hullの大きいものが存在すると考えられます。また、空間群と結晶系のヒートマップにおいて、全体的に空間群を指定したときに三斜晶系(triclinic)がやや現れるのは、このような構造を無理やりMatterSimで構造最適化を行ったため、大きく対称性が崩れたと考えられます。
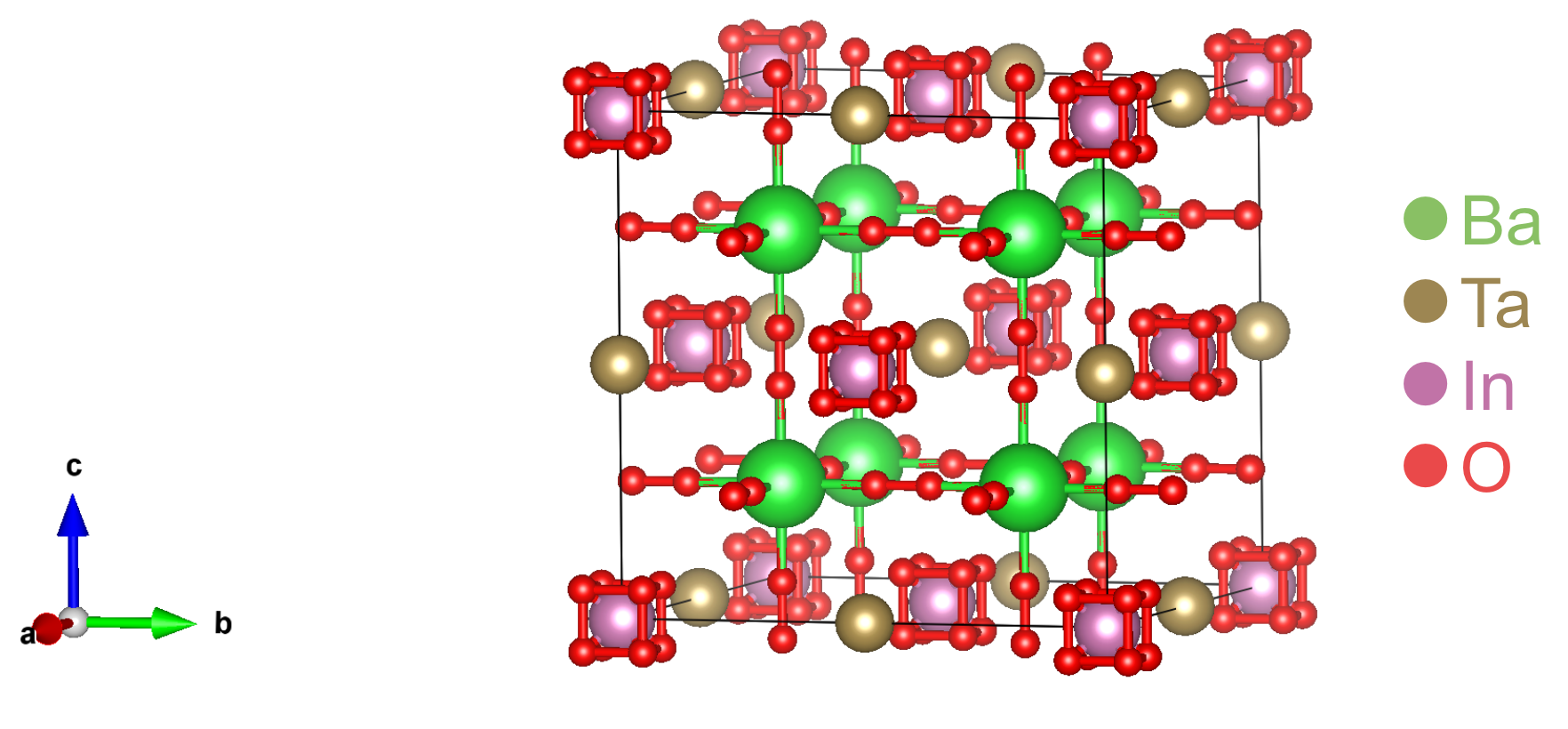
図6.1: Ba-Ta-In-O系の生成(VESTA[10]を用いて描画)
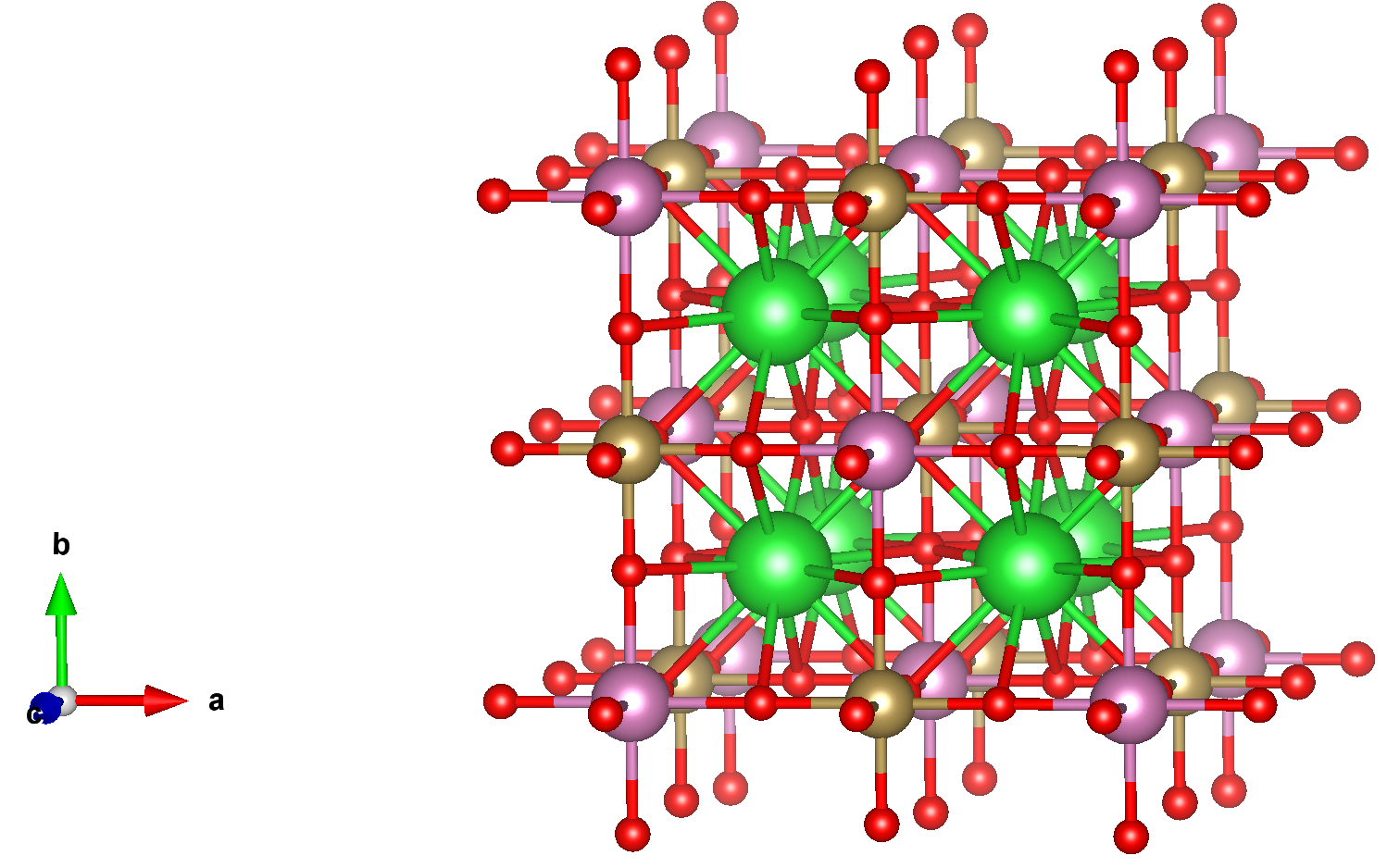
図6.2: Materials Project内に存在するBa2TaInO6(link)
また、WyckoffDiffのもう一つの問題点として一般位置の内部パラメータの情報の消失が挙げられます。一般位置に関しては、内部パラメータの値によって座標の任意性が生じます。しかし、WyckoffDiffが生成するものはWyckoff Element Matrixに基づくprotostructureであり、これには一般位置の内部パラメータの情報がありません。そのため、参照したWyckoffDiffの論文でもPyXtal[11]を用いてsemi-randomに内部パラメータを決めて結晶構造を生成しています。この弊害として、一般位置が重要な結晶構造は生成するのが難しい傾向があります。以下に一例としてスピネル型構造のMgAl2O4の生成を試みた結果を示します。図6.3は同じprotostructure(A2BC4_cF56_227_c_b_e:Al-Mg-O)ですが、酸素サイトの内部パラメータをPyXtalを用いてランダムに生成しているため、図に示しているような異なる構造になります。このようにWyckoffDiffはprotostructureを生成することによる生成速度の利点も挙げられますが、一方で一般位置のような自由度の高い位置の取り扱いが難しいということがわかりました。
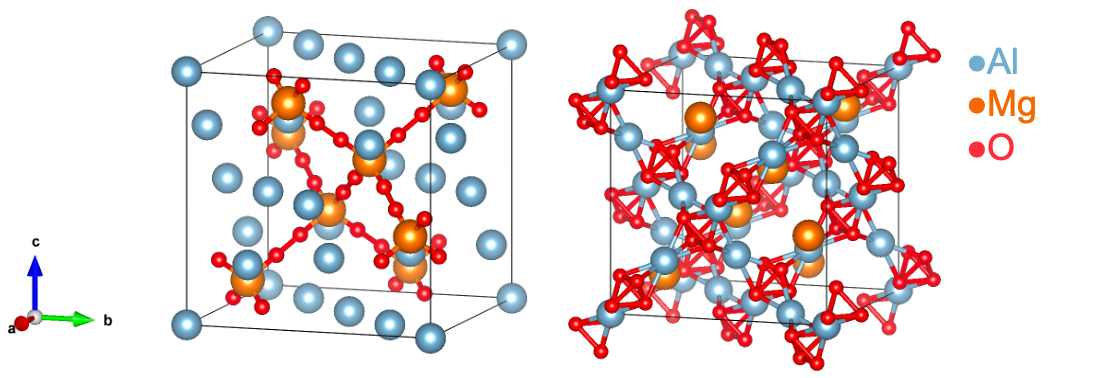
図6.3: 同じprotostructureで異なる結晶構造が生成された例
まとめ
今回のインターンでは、MatterGenの限界を調査し、それを解決するようなモデルとしてWyckoffDiffを採用し、条件付け生成可能にして実験・解析を行いました。その結果以下のことがわかりました。
- WyckoffDiffを用いることで入力で指定した空間群を保つ構造を生成することが可能であり、その結果、MatterGenに比べて対称性の高い構造を生成することが可能
- WyckoffDiffはMatterGenよりも(~6倍程度)高速に結晶構造を生成することが可能
- Li-O系ではMP-20と同程度の安定構造を生成できていることを確認
- 一方で課題点として、高い対称性の構造を生成するが化学結合的に違和感がある系を生成するパターンがあり、そのような系を構造最適化すると、結晶として不安定になり対称性も崩れる
- protostructureから結晶構造の復元は一般位置の座標の任意性があり一対一対応していない
おわりに
インターン期間中に親身に相談に乗ってくださったメンターの久間さん、サブメンターの篠原さんと林さん、またChemチームの皆様にはインターンシップ期間中大変お世話になりました。この場を借りて厚く御礼申し上げます。
参考文献
[1]: Tian Xie et al., ICLR (2022), https://openreview.net/forum?id=03RLpj-tc_
[2]: Rui Jiao et al., arXiv, 2309.04475 (2023)
[3]: Zeni, C., Pinsler, R., Zügner, D. et al. A generative model for inorganic materials design. Nature 639, 624–632 (2025). https://doi.org/10.1038/s41586-025-08628-5
[4]: Filip Ekström Kelvinius et al., arXiv, 2502.06485 (2025)
[5]: Austin, J., Johnson, D.D., Ho, J., Tarlow, D., Berg, R., Advances in Neural Information Processing Systems 34, 17981–17993 (2021)
[6]: H. Yang, et al., arXiv, 2405.04967 (2024)
[7]: Riebesell et al., pymatviz, 10.5281/zenodo.7486816 (2022)
[8]: Horton, M.K., Huck, P., Yang, R.X. et al. Accelerated data-driven materials science with the Materials Project. Nat. Mater. (2025). https://doi.org/10.1038/s41563-025-02272-0
[9]: Jain, Anubhav et al., APL Materials 1, 011002 (2013)
[10]: K. Momma and F. Izumi, J. Appl. Crystallogr., 44, 1272-1276 (2011)
[11]: Scott Fredericks and Kevin Parrish and Dean Sayre and Qiang Zhu, Computer Physics Communications 261, 107810 (2021)




