averaged stochastic gradient descentのご紹介

Tag

# 機械学習

# 解説

preferred

そろそろ寒くなってきましたね。早速風邪を引きました。徳永です。

今日は私の使っている自作の足置き（制作費600円）の紹介でお茶を濁そうと思っていたのですが、途中で方向転換しました。今日は機械学習の話をします。

Léon Bottouという研究者（彼はまたDjVuというドキュメントフォーマットの開発者でもあります）が開発・公開しているsgdというソフトウェアのバージョン2.0が公開されました。sgd 2.0ではaveraged stochastic gradient descent（ASGD）という手法が実装され、これまでのSGDと比べて性能が向上しました。今日はこのASGDを紹介したいと思います。日本語に訳すと平均化確率的勾配降下法でしょうか。漢字が多くて読みづらいので以下ではASGDと呼びます。

もともと、SGD（確率的勾配降下法）はNLPのような高次元かつスパースなタスクではうまく行くということは数年前から言われてきていました。以前に紹介したFOBOSなども、その流れの中に位置づけられるものであると考えています。ASGDはかなり以前、1980年代に提案されたものではありますが、最近になって見直しの動きが始まっているようです。

SGDとは

まずSGDからおさらいしましょう。SGDではデータ一つ一つを使って毎回パラメーター更新を行います。t個目のデータを\(z_t\)、その時の重みベクトルを\(w_t\)、学習率を\(\gamma_t\)、勾配を\(g\)とすると、SGDでは以下のようにパラメーター更新を行います。

\(w_{t+1} = w_t – \gamma_t g(z_t, w_t)\)

見慣れた感じの簡単な式ですね。

勾配のところはどのような目的関数を想定するかで計算方法が変わってきます。ヒンジロス+正則化項ならSVMになりますし、ロジスティック回帰などももちろん使えます。

ASGDとは

実はASGDでも上の部分は全く同じです。違うのは、ASGDでは各時点での重みベクトルの平均を取った重みベクトル\(\overline{w}_t\)というものを考える点です。つまり、\(\overline{w}_t\)は以下の式で計算できます。

\(\overline{w}_t = \frac{1}{t} \sum_t w_t\)

最終的には\(w_t\)ではなく\(\overline{w}_t\)を使いますが、それ以外の点はSGDの場合とプログラムは何も変わりません。

ASGDの効率化

先ほどのASGDの式をそのまま実装すると、各時点での\(w_t\)をそのまま全部保存しておかないといけないことになります。それではさすがにメモリが足りません。

この問題は以下のような式を使って逐次的に\(\overline{w}_t\)を更新することで解決できます。具体的には以下のような形に式を変形します。

\(\overline{w}_{t+1} = \frac{t}{t+1} \overline{w}_t + \frac{1}{t+1} w_{t+1} \)

\(\overline{w}_{t+1}\)を\(\overline{w}_t\)と\(w_{t+1}\)の2つから逐次的に計算するわけです。これでメモリ使用量の問題は解決できます。

毎回こんな式を真面目に計算していると遅くて仕方がありませんが、実際にはFOBOSのlazy updateと同様の工夫を入れることで計算速度の問題も解決できます。

SGDとASGDの比較

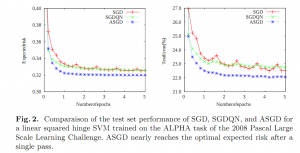
ASGDが実際どれぐらい効果があるのか、実験結果が見てみたいですよね。今回はBottou本人が書いた論文[1]から結果を引用したいと思います。以下の画像は、SVMをSGDとASGDで最適化した結果です。

左側のボックスがExpected Risk、右側のボックスがTest Errorです。Expected RiskはTest Errorのそれぞれのデータサンプルについて\(p(z_t)\)で重み付けして足しあわせたものです。横軸は学習のループ回数です。青い点線がASGD、赤い実線がSGDで、ASGDの方が収束が早く、また収束後の性能でも優れていることがわかります。特筆すべきは、SGDと比べてASGDの方が性能が安定していることです。これは実用上は気を使わないといけないことが1つ減るため重要です。