Blog
本記事は、2019年インターンシップに参加された金川さんによる寄稿です。
こんにちは。PFNの2019夏季インターンシップに参加した、東京大学の金川です。大学では、強化学習を使って賢くロバストなゲームAIを作る研究をしています。
今回のインターンシップでは、「微分可能なシミュレータ上での方策最適化」というテーマで研究を行いました。この記事では、その内容と結果について、簡単に紹介させていただきたいと思います。
なぜ微分可能なシミュレータか
現実世界では、時間が途切れることなく流れているので、次々と行動を決定していかなくてはいけません。そのため現実世界でロボットを動かしたい時にとれる選択肢の一つは、状態Sを観測した時、あらかじめ学習しておいた方策\(\pi(\cdot|S)\)から行動aをサンプリングし、それにしたがって行動させることです。方策が例えばニューラルネットで表現されていれば、各タイムステップで行動計画を最適化する方法と比べ高速に行動を計算できるため、リアルタイム性が求められるドメインでは大きなメリットがあります。
方策を訓練する方法として、強化学習が注目され、さかんに研究されています。強化学習とは、エージェントがある行動をとると次の状態と報酬が返ってくる、というブラックボックスな環境で、報酬和の期待値を最大化するように方策を訓練する枠組みです。強化学習の課題として、しばしばそのサンプル効率の悪さが挙げられます。例えば、昨年のリサーチブログ で紹介されたEmergence of Locomotion Behaviours in Rich Environmentsでは、シミュレータ上のロボットに歩行動作を獲得させるため、1千万回程度ネットワークのパラメタを更新する必要がありました。
しかし、もしブラックボックスな環境を仮定しないならば、シミュレータの内部情報を上手に使って、学習を効率化できるのではないでしょうか。方策としてニューラルネットを使う場合、報酬をネットワークのパラメタについて微分した値が得られれば、それを利用して直接パラメタを更新できそうです。
手法の説明
そこで今回は微分可能なシミュレータを作成し、勾配という形でシミュレータの内部情報をエージェントに渡すことで、効率よく方策を訓練する手法を試みました。具体的に、シミュレータ内部での遷移関数・報酬関数の計算を、微分可能な演算のみに限定します。この演算過程をchainerの提供するdefine by runスタイルの自動微分を使って記述することで、状態遷移・報酬関数をパラメタで微分できるようになります。
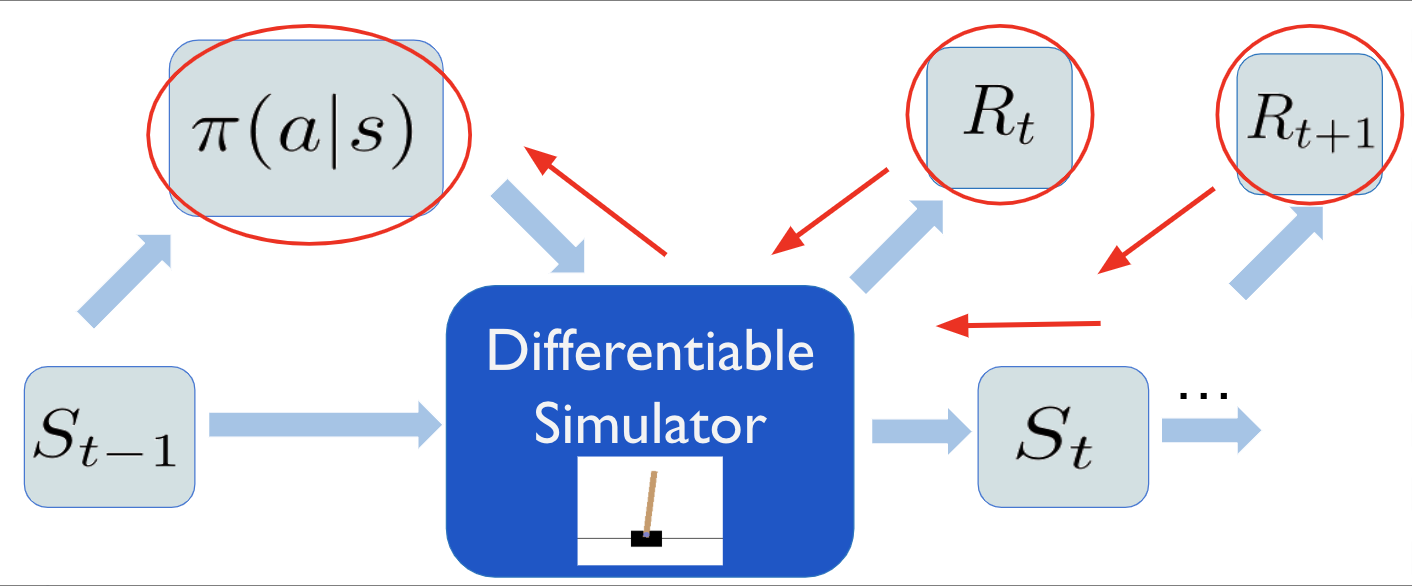
すると、方策と未来の状態・報酬が微分可能な計算グラフでつながり、強化学習における最大化ターゲットである報酬和を、直接方策のパラメタについて微分できます。こうして得られた勾配\(\frac{\partial\sum_{t}\gamma^t R_t}{\partial \theta}\)を使って、方策を勾配上昇法により直接最適化します。
実際のアルゴリズムでは、適当な定数Nをとって、Nステップ分の割引報酬和\(\sum_{t=t_0}^{t_0 + N} \gamma^{t-t_o} R_t\) を最大化します。また学習高速化のため、A2C スタイルの環境並列化およびバッチ学習を行いました。これはシミュレータ内部の物理パラメタをベクトルとして持つだけで、簡単かつ効率的に実装できます。行動についてはすべて連続値をとるものとし、決定的に行動を出力する方策と、行動の正規分布を出力する確率的な方策の2種類を試しました。正規分布からのサンプリングは、再パラメータ化トリック を使うことで逆伝播可能な演算として表現できます。
実験結果
今回のインターンシップではOpen AI gymのClassical Controlタスクを中心に、いくつかの環境をchainerを用いて微分可能なシミュレーションとして実装しました。その上でシミュレータの勾配を使った方策の学習を行って、以下の3点を検証します。
- この手法がうまくいくような問題があるか
- 決定的な方策を使うものと確率的な方策を使うものでは、どちらの性能が良いか
- この手法は、どのような問題に対してうまくいかないか
まず、特に簡単な問題であるCartPole での結果を示します。
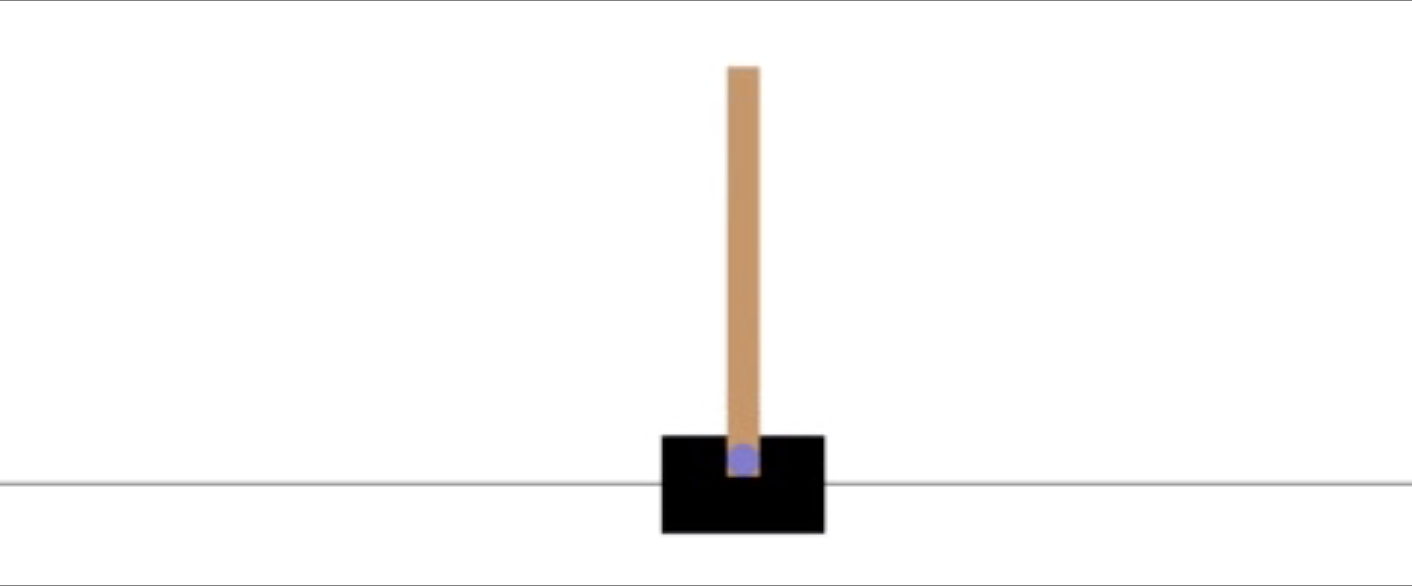
これは、台車に力を加え、上に乗っている棒を安定させる問題です。棒が一定以上倒れるか台車が画面の外に出ると、ゲームオーバーになります。
オリジナルの問題での行動は、 「-1or1の力を加える」という離散的でなものですが、今回の設定では[-1, 1]の連続値をとるように変更しました。報酬についてはオリジナルの問題ではゲームオーバーなら0、それ以外なら1が貰えますが、今回は微分可能になるように改造した \(1.0 -\frac{2|\theta |}{\pi} \) を与えました。実装した他の環境に対しても同様に、なるべく元の問題と変わらないよう行動を連続値に、報酬を微分可能にする変更を行っています。
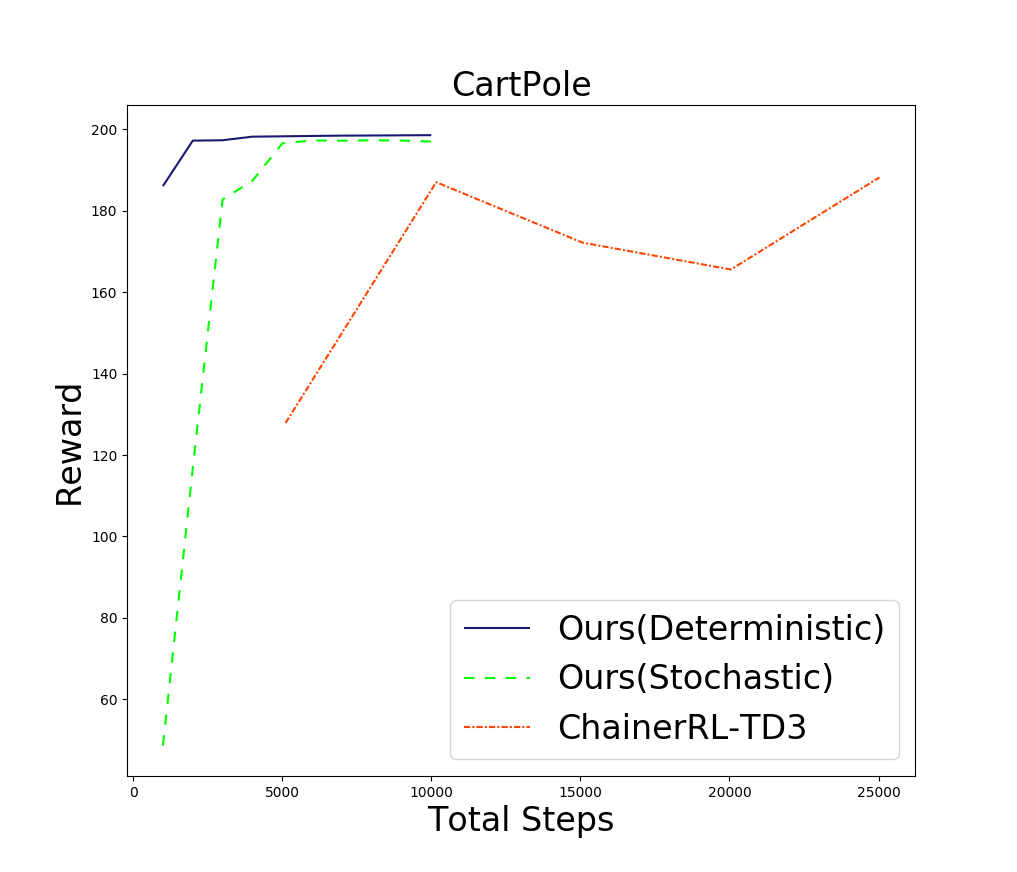
上図に結果を示します(シミュレータのステップ数で性能を比較していますが、同じステップ数の場合ネットワークの更新回数は提案手法の方が20倍程度少ないです。)
どちらの方策を使う場合も、ベースラインとして使用した深層強化学習の手法(TD3) と比べ、20倍以上早く収束していることがわかります。
次にFlappyBirdでの実験結果を示します。これは元々iOS向けに公開されていたゲームですが、今回はOSSとして公開されているPythonクローン をもとに、chainerにより再実装しました。
ゲームの内容としては、鳥に上方向の力を加え土管にぶつからないように飛行させる、という単純なものです。オリジナルの問題では画面をタップするとかなり強い力が加わりますが、今回は連続値の力を加えるため、やや簡単になっています。しかし内部状態(=位置、速さ、角度など)だけが与えられた先程のCartPoleと比べると、この問題では土管の位置など多様な観測情報をもとに行動決定を行う必要があるため、学習は難しくなりそうです。下図に、実験の結果を示します。
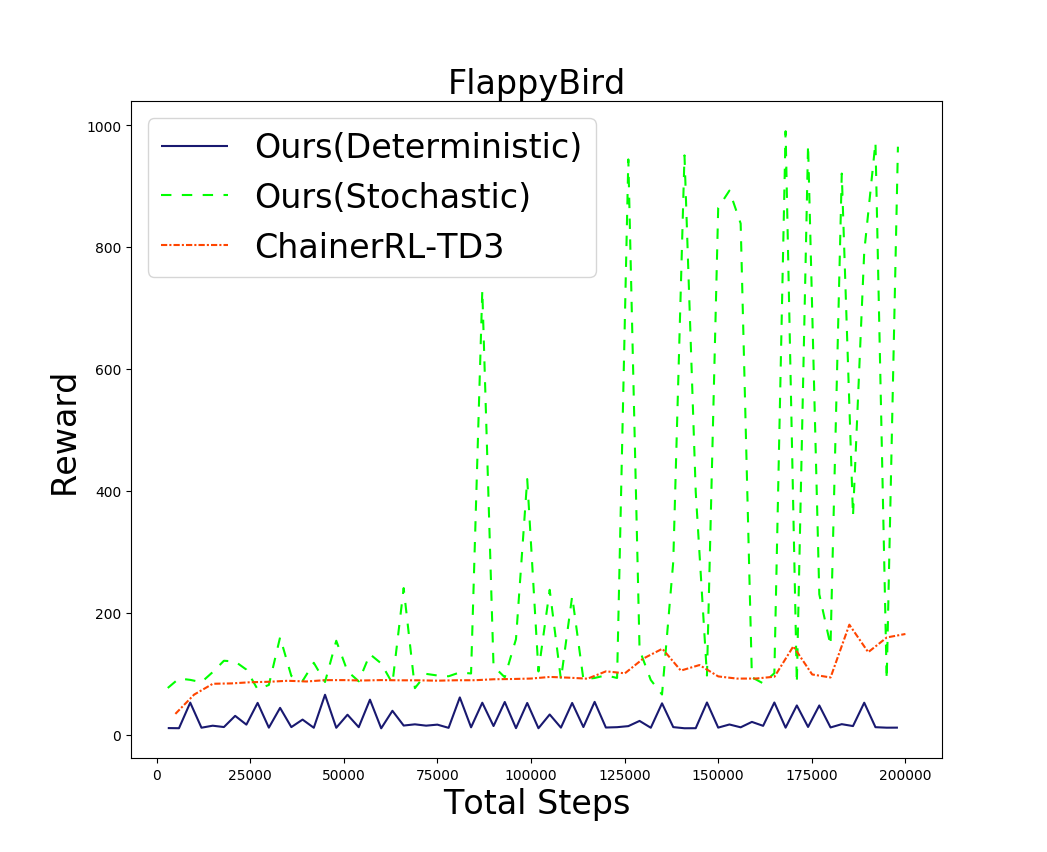
実際に行動を観察(上図左)してみると、スタート直後から急激に上昇し、画面外で土管に激突していることがわかります。
この原因について考えるため、この手法での最大化ターゲット\(\sum_{t=t_0}^{t_0 + N} \gamma^{t-t_o} R_t\) を再訪してみましょう。方策を変えれば将来貰える報酬は変化しますから、この式は現在の方策のもとでの報酬の期待値\(\sum_{t=t_0}^{t_0 + N} \mathbb{E}_\pi \left[ \gamma^{t-t_o} R_t\right]\) (…式1) を最大化しています。
そのため方策がランダム性を持っていないとき、局所最適解に陥りやすくなってしまうのです。強化学習では、局所最適に陥らないよう広範な行動データを収集する必要があり、そのための行動を探査(exploration)といいます。
一方で確率的な方策を使うものは、やや不安定ではあるもののベースラインを大きく上回る性能を残しています。この問題では探査に成功しているようです。(上図右)に示すように、飛行動作も安定しています。
以上の2つの実験から、この手法が単純な状態遷移のダイナミクスを持つ問題に対しては非常にうまくいくこと、探査が必要な問題では確率的な方策の方が性能がよいことがわかりました。
しかしもっと複雑な、カオス的な挙動をする系では、少しの方策の違いが将来の報酬を大きく変動させます。そのため式(1)の分散は非常に大きくなり、学習は難しくなりそうです。
カオス的な問題として、CartPoleSwingUp(下図)での実験を行いました。これは先程のCartPoleとほとんど同じ問題ですが、通常のCartPoleで初期位置がθ=0の近傍から始まるのに対し、θの値が[-π, π]からランダムに与えられます。
この変更はダイナミクスに強い非線形性をもたらすだけでなく、探査も難しくします。
報酬については原論文に似せた \(\frac{\cos (\theta) + 1)}{2} \)を使用しました。下図に結果を示します。
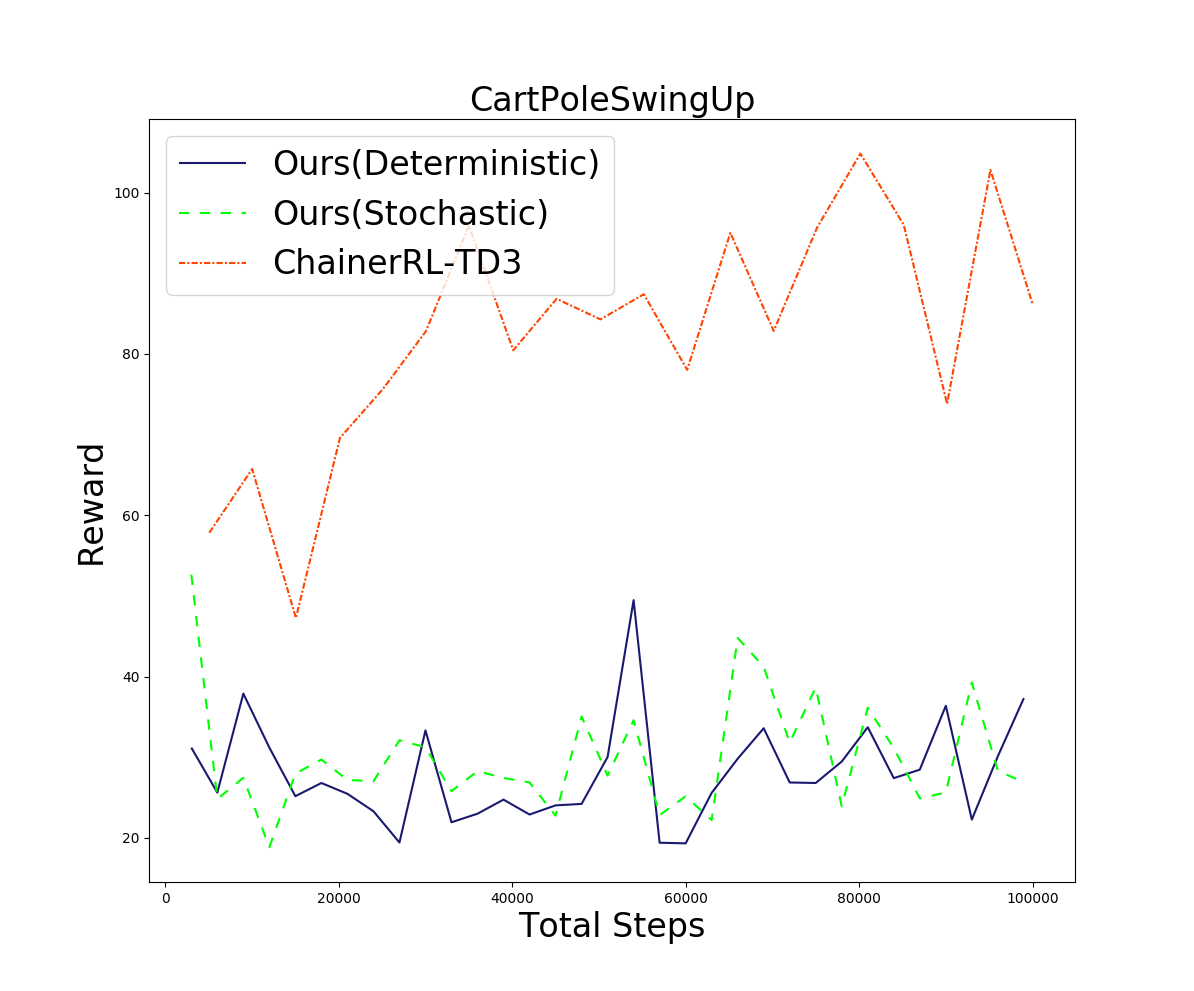
どちらの方策を使う場合も、ベースラインより大きく劣るという結果になりました。
次に探査に失敗する例として、MountainCar(下図)での結果を紹介します。この問題では右上の旗にたどり着かないと正の報酬が貰えませんが、そのためにはいったん左の坂を登って勢いをつけないといけません。

下図に結果を示します。
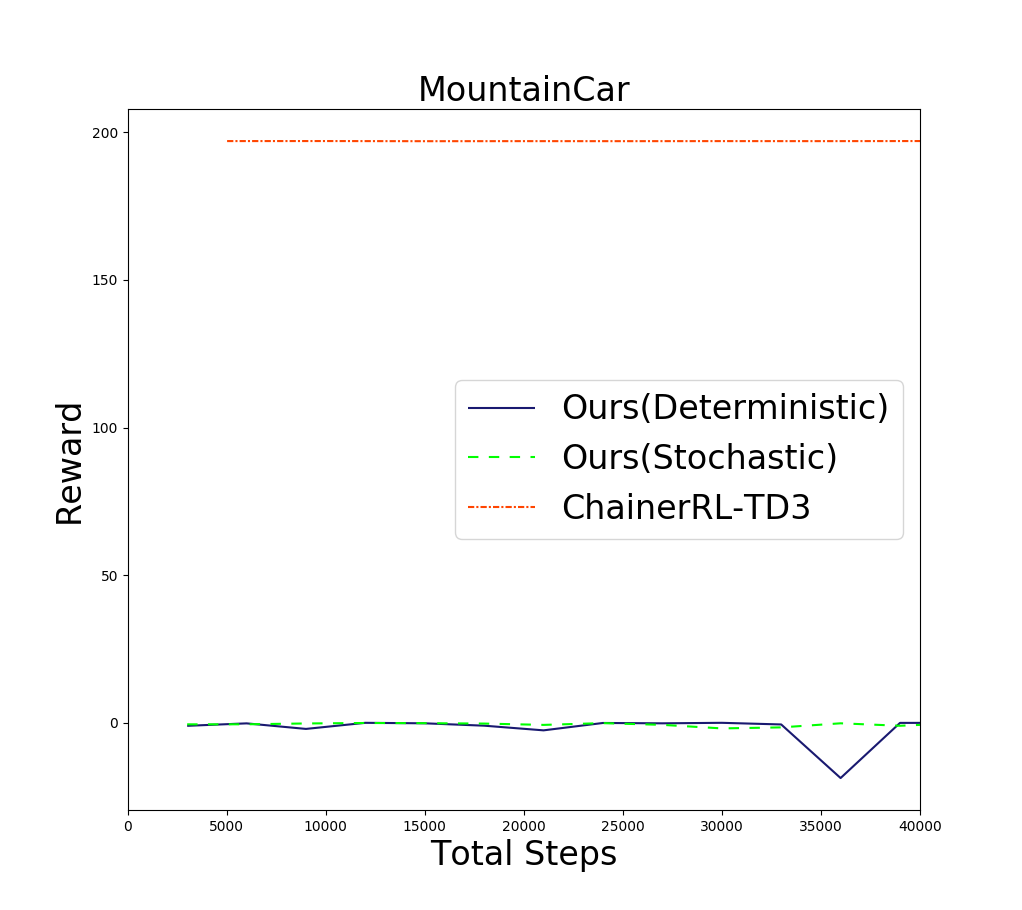
これも、ベースラインよりはるかに劣るという結果になりました。
この問題では車を動かすため使用した燃料の量に応じて負の報酬が入りますが、それに過剰に反応し、なるべく力をかけないような方策を学習してしまいます。
以上の2つの実験から、この手法がカオス的なダイナミクスを持つ問題や、局所最適に陥りやすい問題に対してはあまり性能が出ないことがわかりました。
まとめ
微分可能な物理シミュレータは新しい研究分野です。決定的な方策を最適化するもの や物理パラメタの推定に用いるもの などが提案されていますが、いまだにロボット制御など複雑なシミュレータで検証を行った研究は、我々の知識ではありません。そのため今回のインターンでトイモデルではあるものの、様々な問題で微分可能シミュレータ上での方策最適化の性質を調べられたことは、この手法をより複雑なドメインへ適用するために大きくプラスになったと考えています。
今回の実験では様々な課題が見つかり、単にシミュレータを微分可能にすれば何でもうまくいくという訳ではない、ということがわかりました。しかし簡単な問題では性能が出ることを確認できましたし、またシミュレータ自身が訓練可能になるなど、今回は検証できなかった多くの興味深い性質を持っています。今後も様々な側面から、微分可能シミュレータの可能性を探っていければと思います。
謝辞
慣れないテーマで困惑することや大変に感じることもありましたが、メンターのお二方、インターン同期の方々、同じチームの方々と相談しながら楽しく作業を進めることができました。ありがとうございました。
おまけ:メンターより
金川さんのメンターを担当した、PFNの中須賀と今城です。
PFNでは微分可能シミュレーションの研究開発を行っています。微分可能シミュレーションによって初期値同定など様々な問題が解けることがわかりつつありますが、ただオプティマイザーに投げるだけでは十分な探索が行われないがゆえの問題があり、これを強化学習のアイディアをうまく取り入れて解決できないかということで始まったプロジェクトでした。金川さんには短い期間で様々なアプローチで強化学習のアイディアを取り入れ検証し微分可能シミュレータの可能性を見出していただきました。
深層学習をただ適用するだけではなく問題の性質を考えた学習方法を提案できるというのがPFNの強みの一つであり、問題の性質を理解したり新たな学習方法を理解し現実で解かれていない難しい問題を解くために、このように基礎研究に近いようなアイディアから取り組むということも行っています。今回のプロジェクトはそのような取り組みの一環でもあります。興味のある学生の皆さんは、ぜひ来年のPFNインターンシップへの応募をご検討ください。 また、もちろん中途・新卒の人材募集も通年で行っていますので、こちらも興味のある方はぜひご検討ください!PFNの人材募集のページはこちらです。




