Blog
本記事は、2019年インターンシップとして勤務した新幡 駿さんによる寄稿です。
こんにちは、2019年夏にPFNでインターンをしていた新幡です。大学では連続最適化の研究室に所属しています。PFNでは、モデル予測制御 (MPC; Model Predictive Control) を「微分可能」にするAmosら (2018) の論文“Differentiable MPC for End-to-end Planning and Control”[1] について、著者によるPyTorch実装のChainerへの移植と追加実験を行いました。MPCはモデルを用いて将来の状態を予測しながら制御を行う手法であり、化学プラントの制御などに用いられています。
【2019/10/7追記】Chainerへの移植実装はGitHubで公開しています。
https://github.com/pfnet-research/chainer-differentiable-mpc
1. OptNet
Amosらは、2017年に二次計画法を微分可能にする層として“OptNet: differentiable optimization as a layer in neural networks”[2] を提案しました。二次計画法を微分可能にすることで、勾配降下法を用いて二次計画法の目的関数や制約条件を、ネットワークの損失関数に対して最適化することができます。OptNetの順伝播は、二次計画問題を主双対内点法という収束するまで反復を繰り返す方法を用いて解いています。OptNetの誤差逆伝播は、主双対内点法を全て連鎖律で逆にたどるのではなく、最適解の満たすべき条件のうち等式で書けるもの (KKT行列) から効率的に偏微分を求めています。大量のデータを用いて学習する為に、二次計画問題を大量に解く必要があるので、Amosらはバッチで計算できるような主双対内点法を実装しており、著者実装は A fast and differentiable QP solver for PyTorch として公開されています。また、副メンターの酒井さんによるChainerへの移植の試みとして chainer-optnet があります。
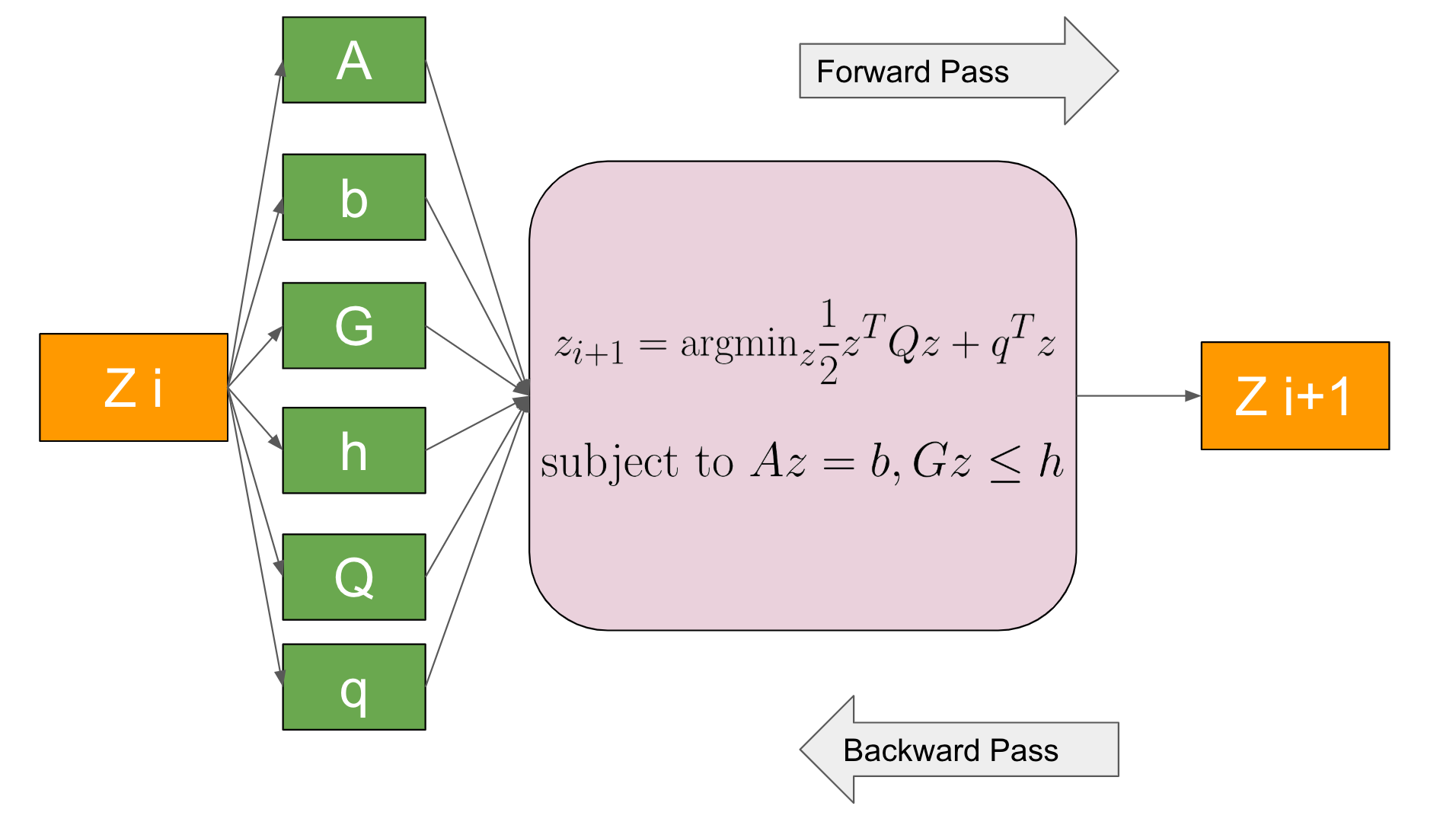
図1. OptNetの概要図
2. Differentiable MPC
OptNetで二次計画法を微分可能にする手法が提案されたので、有限離散時間線形二次レギュレータ (Linear-Quadratic Regulator; LQR) などの二次計画法を用いて解ける最適制御問題はOptNetを用いて微分可能にできます。しかし、LQRを二次計画問題として解くのではなく、動的計画法を用いた方が効率的に解くことができることが知られています。Amosらは、LQRの順伝播の計算に動的計画法を用い、誤差逆伝播の計算もKKT行列の時間的構造を用いてOptNetより効率的に微分を求められるLQRを提案しました。
さらに有限離散時間MPCのようなコスト関数やダイナミクスが非線形な問題に対しても、微分可能にした論文がAmosらによるDifferentiable MPCです。著者による実装はアルゴリズムの主な部分が mpc.pytorch としてライブラリになっており、著者の実験コードは differentiable-mpc というレポジトリにあります。
3. 前提知識
3.1. LQR
LQRは一般的には、コスト関数が二次でダイナミクスの制約が線形、操作量が無制約な次のような形で表される最適制御問題です。
$$
\begin{align*}
&\underset{\tau_{1:T}}{\text{minimize}} & & \sum_t \frac{1}{2} \tau^T_t C_t \tau_t+c^T_t \tau_t \\
&\text{subject to} & & x_1 = x_\text{init}\\
& & & x_{t+1} = F_t \tau_t + f_t
\end{align*}
$$
ここで \(x\) は状態、 \(\tau\) は状態と操作量を連結したもの、 \(C\) はコスト関数の二次の項を表す行列、 \(c\) はコスト関数の1次の項を表すベクトル、\(F\) はダイナミクスを表す行列になります。Amosらは、LQRを動的計画法を用いて、ベルマン方程式を再帰的に解くことで解いています。詳しくは[3]を参照してください。
3.2. MPC
MPCはLQRと異なり、コスト関数は2次に限らず、ダイナミクスも線形に限りません。さらに、操作量に制約がつく場合もあります。元論文で扱ったMPCは以下の式です。
$$
\begin{align*}
&\underset{\tau_{1:T}}{\text{minimize}} && \sum_t C_{\theta, t}(\tau_t) \\
& \text{subject to } && x_1= x_{\mathrm{init}}\\
&&& x_{t+1} = f_{\theta}(\tau_t)\\
&&& \underline{u} \leq u \leq \overline{u}
\end{align*}
$$
Amosらは、コスト関数を二次近似、ダイナミクスを一次近似して、収束するまでLQRソルバを繰り返し用いるiLQRという手法を用いて解いています。また、制約については、Tassaら (2012) による“Control-Limited Differential Dynamic Programming”[4] と同じように扱っています。
4. 応用
Differentiable MPCの応用として、Amosらが行っているのがエキスパートの操作列を模倣する模倣学習 (imitation learning) です。Amosらによる模倣学習は、ダイナミクスやコスト関数をパラメータ化した形で表して、エキスパートの操作列との二乗誤差をネットワークの損失関数としてパラメータを最適化させています。最適化によって得られたダイナミクスやコスト関数をMPCに用いることで、エキスパートの操作列を模倣する方策を得られると期待できます。Amosらは、実験設定として、倒立振子 (inverted pendulum) を題材に、学習するものがダイナミクスのパラメータのみ・コスト関数のパラメータのみ・両方の三通りの学習を試しています。

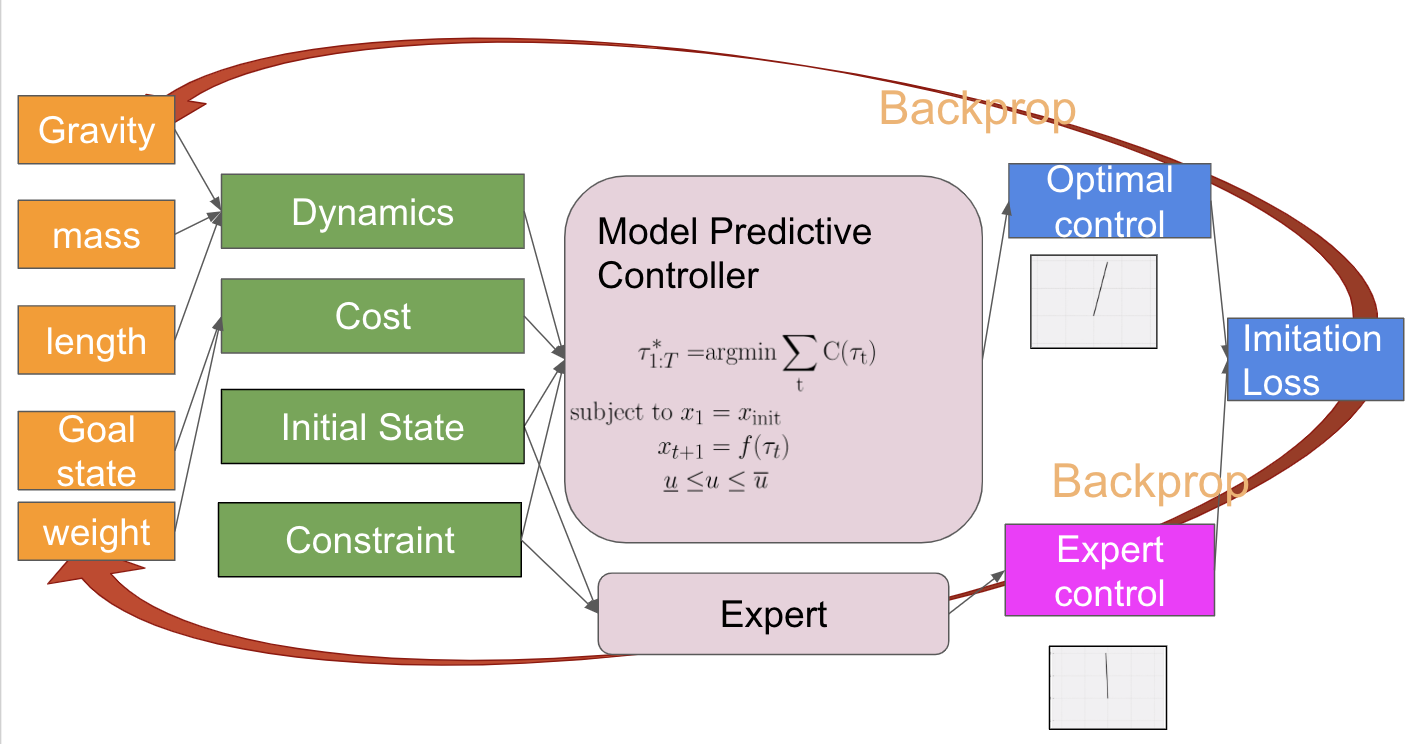
図2. 模倣学習の設定
例として、ダイナミクスを既知として、コスト関数をパラメータ化した形で学習を行うと次のようになります。エキスパートの操作列から、正しく倒立振子を安定化させることができていることがわかります。

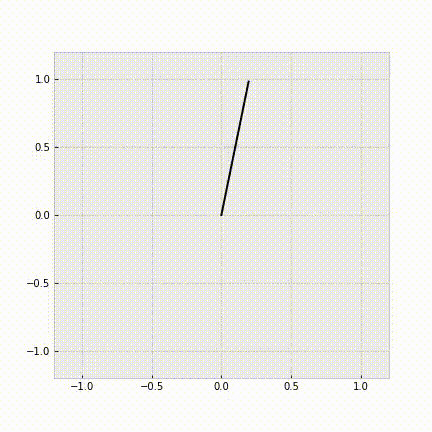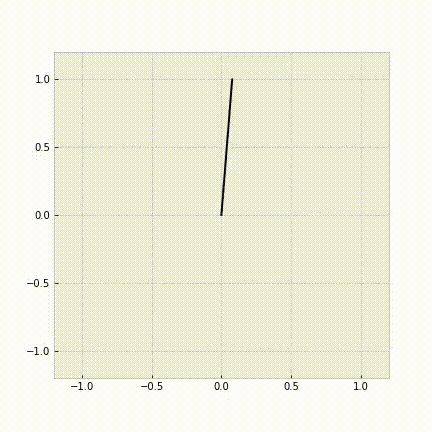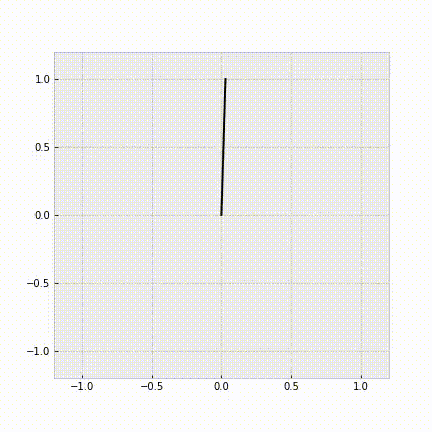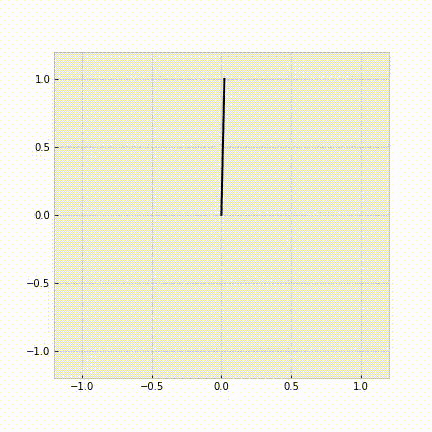
図3. 学習したコスト関数を用いた制御
5. 追加実験
追加実験として、コスト関数をAmosらのように特定の形にパラメータ化した形ではなく一般の二次関数の場合もうまく学習できるのかを試しました。ここでAmosらのパラメータ化を詳しく説明すると、以下の数式のようになっていて、\(q_{\text{logit}}\)と\(p\)という二つのベクトルをパラメータとしています。
$$
\begin{align*}
q &= \mathrm{sigmoid}(q_{\rm{logit}})\\
C(\tau) &= \frac{1}{2}\tau^T q \tau + (\sqrt{q} \circ p)^T \tau
\end{align*}
$$
追加実験として試したパラメータ化は、半正定値行列\(Q\)とベクトル\(p\)をパラメータとして用いてコスト関数をより多くのパラメータで表現しています。
$$
\begin{align*}
C(\tau) = \frac{1}{2}\tau^T Q \tau + p\tau
\end{align*}
$$
5.1. 真のコスト関数がAmosらのパラメータ化で表現できる場合
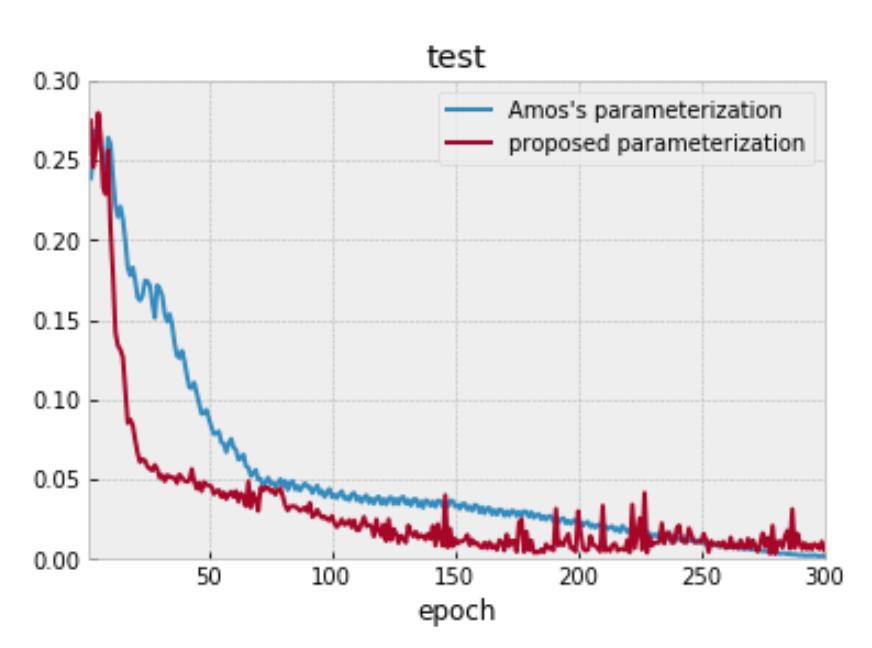
図4. 真のコスト関数がAmosらのパラメータ化で表現できる時
この場合は、真のコスト関数の構造を取りいれているAmosらによる手法の方が損失関数の値が下がりました。
5.2. 真のコスト関数がAmosらのパラメータ化で表現できない場合
真のコスト関数がAmosらのパラメータ化で表せないように問題設定を変えました。
この場合、一般的な二次関数のパラメータを用いた手法とAmosらの手法を比較すると、損失関数がどの程度まで下がるかは同等でした。Amosらの手法では、真のコスト関数を表現できないので、一般的な二次関数を用いて学習させる方が損失関数の値が下がることを期待していたのですが、これは意外な結果でした。Amosらは、LQRの場合に、ダイナミクスを一般的な行列の形にして模倣学習を行い、その際は半分程度は損失関数がうまく下がらないという現象を確認していますが、これを模倣学習の損失関数が、ダイナミクスのパラメータに対して、勾配降下法では最適化することが難しい非凸な関数であったからと結論づけています。今回、一般的な形のコスト関数でうまく学習できなかったのも、コスト関数を一般的な形にすると、損失関数がコスト関数のパラメータに対して非凸な関数になったからではないかと考えられます。

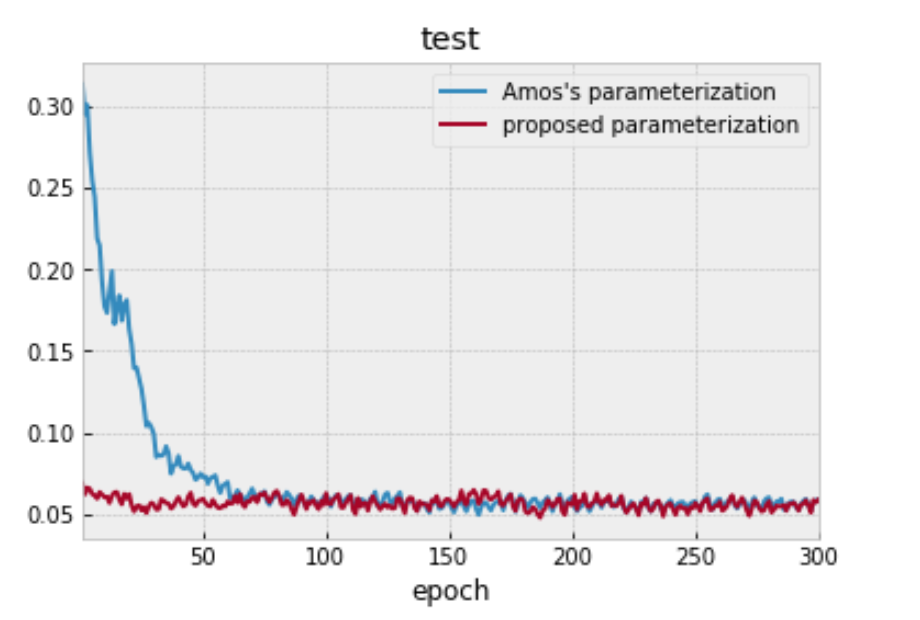
図5. 真のコスト関数がAmosのパラメータ化で表現できない時
6. 感想
今回のインターンでは、Differentiable MPCのChainerへの移植を行い、色々と実験設定を変えてみました。コスト関数を凸なニューラルネットワークで置き換えられるとおもしろそうだなという思いつきから、まずはコスト関数のパラメータを増やして実験してみました。元論文では模倣学習の損失関数が制御器のパラメータに関して非凸な関数になることがあると指摘されており、追加実験でもパラメータを増やしたところあまり損失関数の値が下がらないという結果になりました。
Differentiable MPCは理論、実装共にかなり複雑で、Chainerにライブラリを移植するのにかなり苦労し、時間がかかってしまいましたが、メンターさん方の助けもあってなんとかできました。ありがとうございました。
参考文献
[1] B. Amos, I. Jimenez, J. Sacks, B. Boots, and Z. Kolter. “Differentiable MPC for End-to-end Planning and Control” In NIPS’18 Proceedings of Advances in Neural Information Processing Systems. Available: https://arxiv.org/abs/1810.13400
[2] Brandon Amos, and J. Zico Kolter, “OptNet: differentiable optimization as a layer in neural networks” In ICML’17 Proceedings of the 34th International Conference on Machine Learning. Available: https://arxiv.org/abs/1703.00443
[3] Sergey Levine. Optimal control and planning. berkeley cs 294-112: Deep reinforcement learning. Available: http://rail.eecs.berkeley.edu/deeprlcourse-fa17/f17docs/lecture_8_model_based_planning.pdf
[4] Yuval Tassa, Nicolas Mansard and Emo Todorov. “Control-Limited Differential Dynamic Programming” ICRA’14 IEEE International Conference on Robotics and Automation. Available: https://homes.cs.washington.edu/~todorov/papers/TassaICRA14.pdf
メンターからのコメント
メンターを担当したPFNの飯田と酒井です。
PFNは深層学習に強みがありますが、現実の問題を解決するには深層学習だけでは不十分なこともあり、最適化や制御の技術を組み合わせて用いることも多いです。しかし、昨年までのインターンシップではそういったバックグラウンドの学生の方にはあまりリーチ出来ていませんでした。
そこで、今年のインターンシップ募集でのテーマ「機械学習アルゴリズムの応用 (数理最適化、シミュレーション、時系列予測など) に関する研究開発」では「数理最適化」もキーワードに含め、結果として最適化のバックグラウンドを持つ学生さんとの研究開発を幾つか実施することができました。微分可能MPCに関するこのテーマはその一つです。
今回のテーマは、再現実装の負荷がメンター二人の想定していたよりも重く、新幡さんには随分苦労させてしまいましたが、再現実装と追加実験までを行っていただくことができました。社内の他のプロジェクトでも深層学習とMPCを組み合わせて用いており、今回の新幡さんの成果も今後それらにうまく活用していきたいと考えています。




