Blog
この記事は、金融チームのインターンの吉田凌也さんによる寄稿です。
はじめに
こんにちは!2024年度夏季インターンシップに参加させていただきました、東京大学修士1年の吉田凌也です。
今回のインターンシップでは、条件付き拡散モデルを用いた金融時系列の生成に取り組みました。
背景
金融時系列生成の意義
金融取引戦略とは、金融市場での取引で買い・売り注文を出すタイミングなどの取引規則を決めたものです。実際に戦略に従って資金を運用して利益獲得を目指す前に、その戦略を評価する必要があります。
それには、過去の金融時系列を用いるバックテストが最もよく使われます。
バックテストとは、取引戦略を過去の金融時系列でシミュレーションし、どのくらいの利益が、どのくらい安定的に得られるのかを評価する方法です。
しかし、バックテストでは過去実現したシナリオでしか評価できず、将来起こりうるシナリオを網羅するような評価を行えません。
そこで、金融時系列生成が注目されています。
もし金融時系列の生成ができたら、将来起こりうる様々なシナリオを生成することによって、戦略を多面的に評価することができます。
例えば、実データでは滅多に起こらない暴落に対する性能評価ができることで、実際に暴落が起きてしまった場合に戦略がどの程度損失を出してしまうかを把握することができます。
これは戦略の性能評価のために重要です。
先行研究
“Quant GANs: Deep Generation of Financial Time Series“や”Modeling financial time-series with generative adversarial networks“では、金融時系列生成のためにGANを用いていました。拡散モデルの台頭以降では、”CSDI: Conditional Score-based Diffusion Models for Probabilistic Time Series Imputation“というものが拡散モデルによる時系列補間の先行研究であり、株価時系列生成にも成功しています。
条件付き拡散モデルを用いて所望のトレンドを得る先行研究に、”拡散モデルを用いた条件付き金融時系列データ生成“があります。
条件付き拡散モデルを用いて、所望のトレンドの対数リターン系列の生成に成功しています。
やったこと
今回は、実金融時系列データの代わりとして資産価格過程のシミュレーター(PEHedge内の実装)により生成したものを学習用・評価用データとして用いました。
実データよりシミュレーションデータの方が価格変動の解釈が容易であり、より詳細な考察ができます。
最終的には実データを用いて拡散モデルを学習させ、実データの分布を捉えたモデルを構築しますが、拡散モデルが金融時系列の分布を捉えられるかを確認しておく必要があります。
そのため、まずはシミュレーションデータを用いた検討を行い、シミュレーションで与えたパラメータを捉えられるかどうかを確認することで、金融時系列を捉えられているかを評価しました。
条件付き拡散モデルのノイズ予測ネットワークにはTransformerを使用しています。
対象とする価格過程
PFHedgeによるシミュレーションでデータを生成するにあたり、2つのプロセスを対象としました。これらは実際の金融時系列のモデルとしても使われるものです。
Brownianプロセス
オプションという金融商品の価格計算のために使用される、最も基本的なモデルです。
価格がランダムに動きますが、ボラティリティは一定という仮定をおいています。
ただし、ボラティリティとは価格の動きの変動性を表す量で、対数リターンの標準偏差から計算されます。
プロセスは以下のような式で表されます。
\(dS(t) =\mu S(t)dt+\sigma S(t)dW(t) \)
ここで、S(t)は時刻tにおける価格、W(t)はブラウン運動です。\(\mu\)はドリフト項で、基本的なトレンドの方向を表します。
\(\sigma\)はボラティリティです。
Hestonプロセス
Brownianプロセスの「ボラティリティが一定である」という強い仮定を外し、より実金融市場での値動きを反映するモデルです。ボラティリティを変動させることで、実金融市場で観測されるボラティリティクラスタリングという現象をモデリングすることができます。ボラティリティクラスタリングとは、一度ボラティリティが高い(低い)状態に入ると、その状態がしばらく維持される現象のことです。
プロセスは以下のような式で表されます。
\(dS(t) =\sqrt{V(t)}S(t)dW_S(t)\)
\(dV(t) =\kappa (\theta -V(t))dt+\sigma\sqrt{V(t)}dW_V(t)\)
ここで、S(t)は時刻tにおける価格、\(\sqrt{V(t)}\)はボラティリティです。
\(W_S\)と\(W_V\)は相関のあるブラウン運動で、\(dW_S(t)・dW_V(t)=\rho dt\)という関係があり、\(\rho\)は一般に負の値をとります。
\(\theta\)はボラティリティの長期平均で、\(\kappa\)はボラティリティが\(\theta\)に回帰する速度を表し、\(\sigma\)はボラティリティの標準偏差です。
実験内容と結果
128データポイントを1サンプルとし、上記のプロセスの式のパラメータのうち1つを条件付けの対象として、PFHedgeにより価格系列のデータセット(学習用データ・評価用データ)を生成しました。なお、いずれも与える条件は半分ずつ、同数与えました。
それを用いて価格系列を生成できるような条件付き拡散モデルを学習させ、学習済みモデルの生成データと評価用データを3つの評価方法で比較しました。
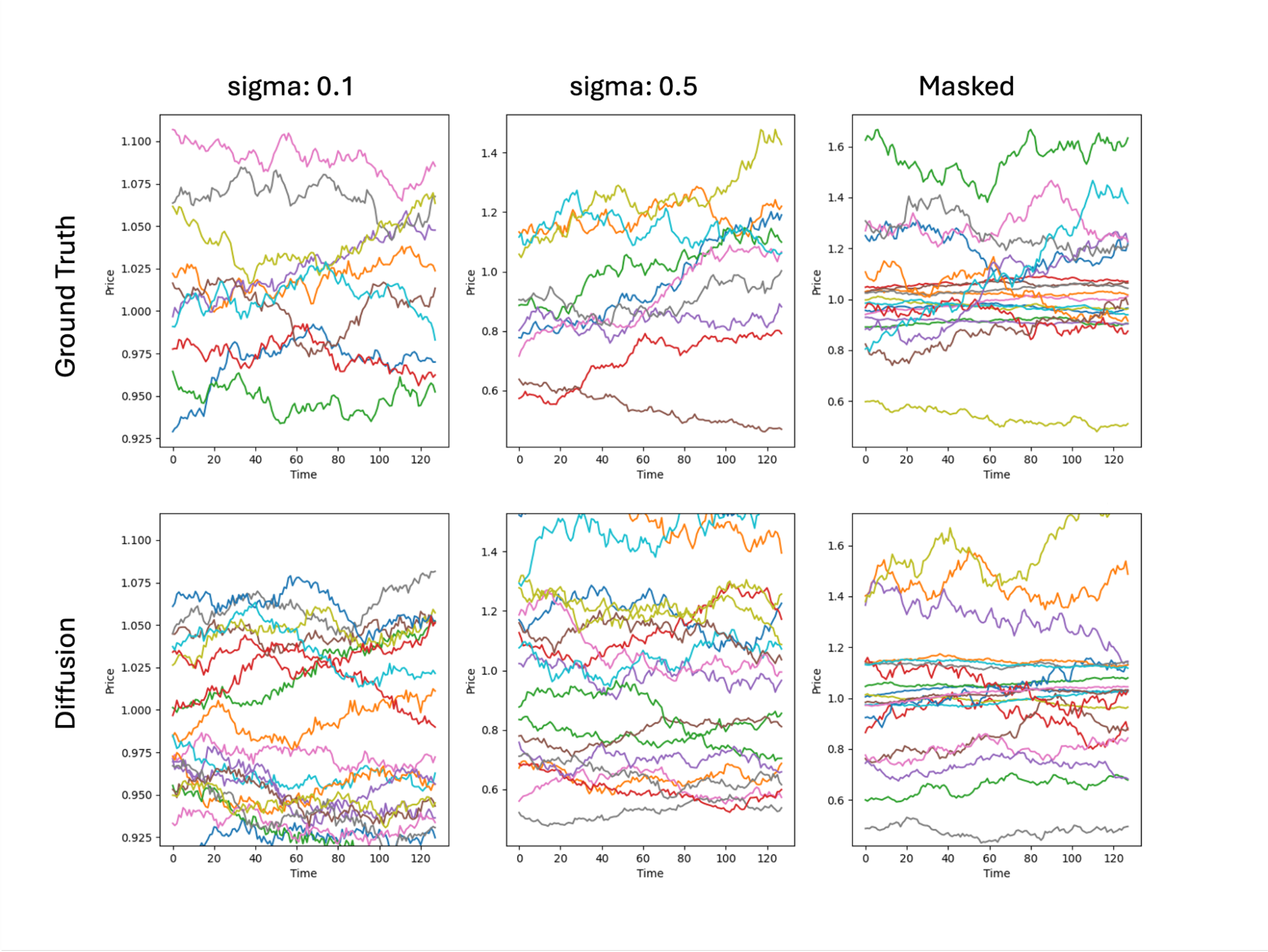
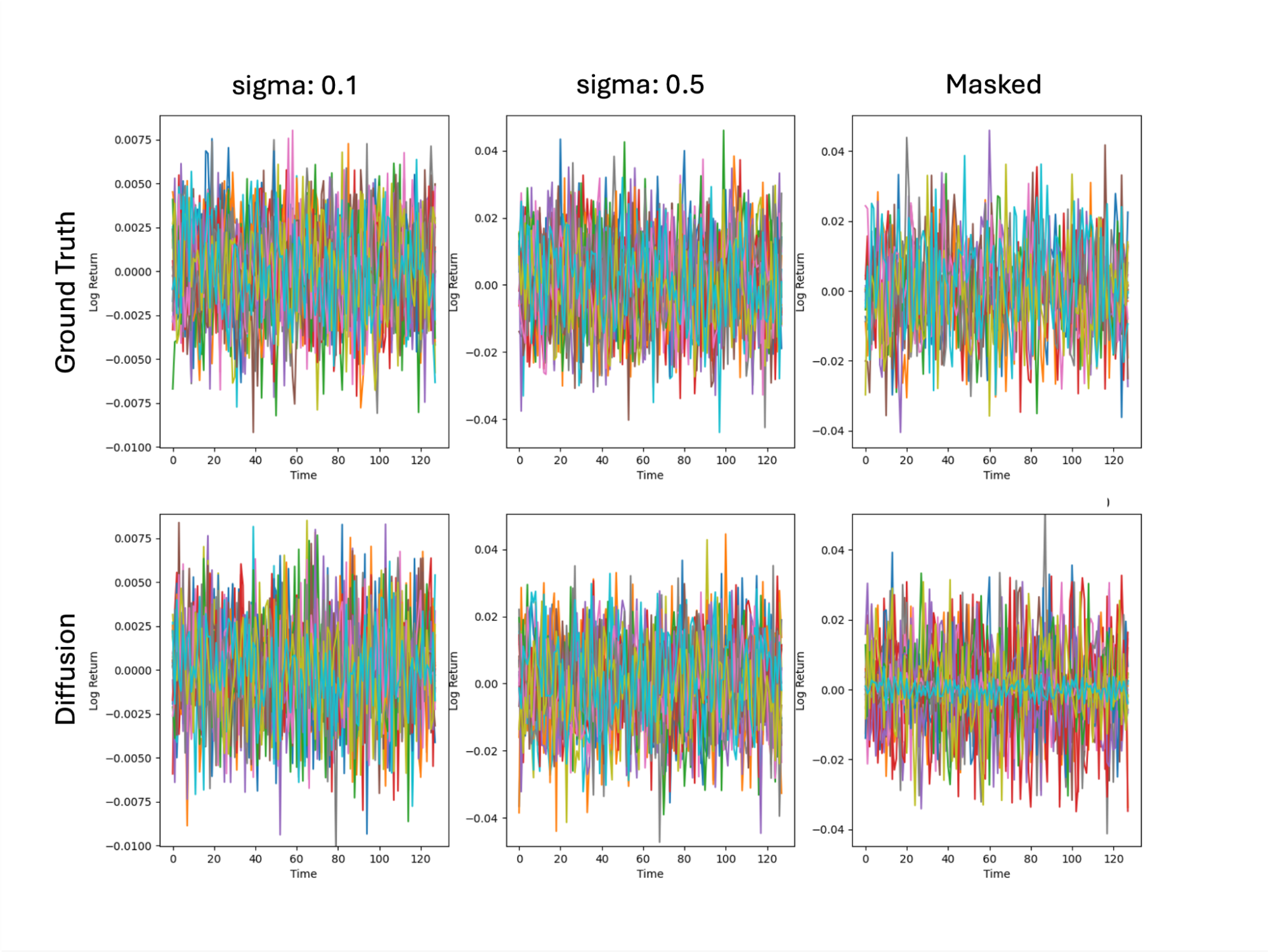
Brownianプロセス
ボラティリティはトレンドの特性を規定する重要な量の1つであり、後の定量評価がやりやすいという
理由で、今回はボラティリティ\(\sigma\)を条件付けの対象としました。\(\sigma\)は0.1と0.5の2値で与えています。
評価1: 価格系列と対数リターン系列の定性的な比較
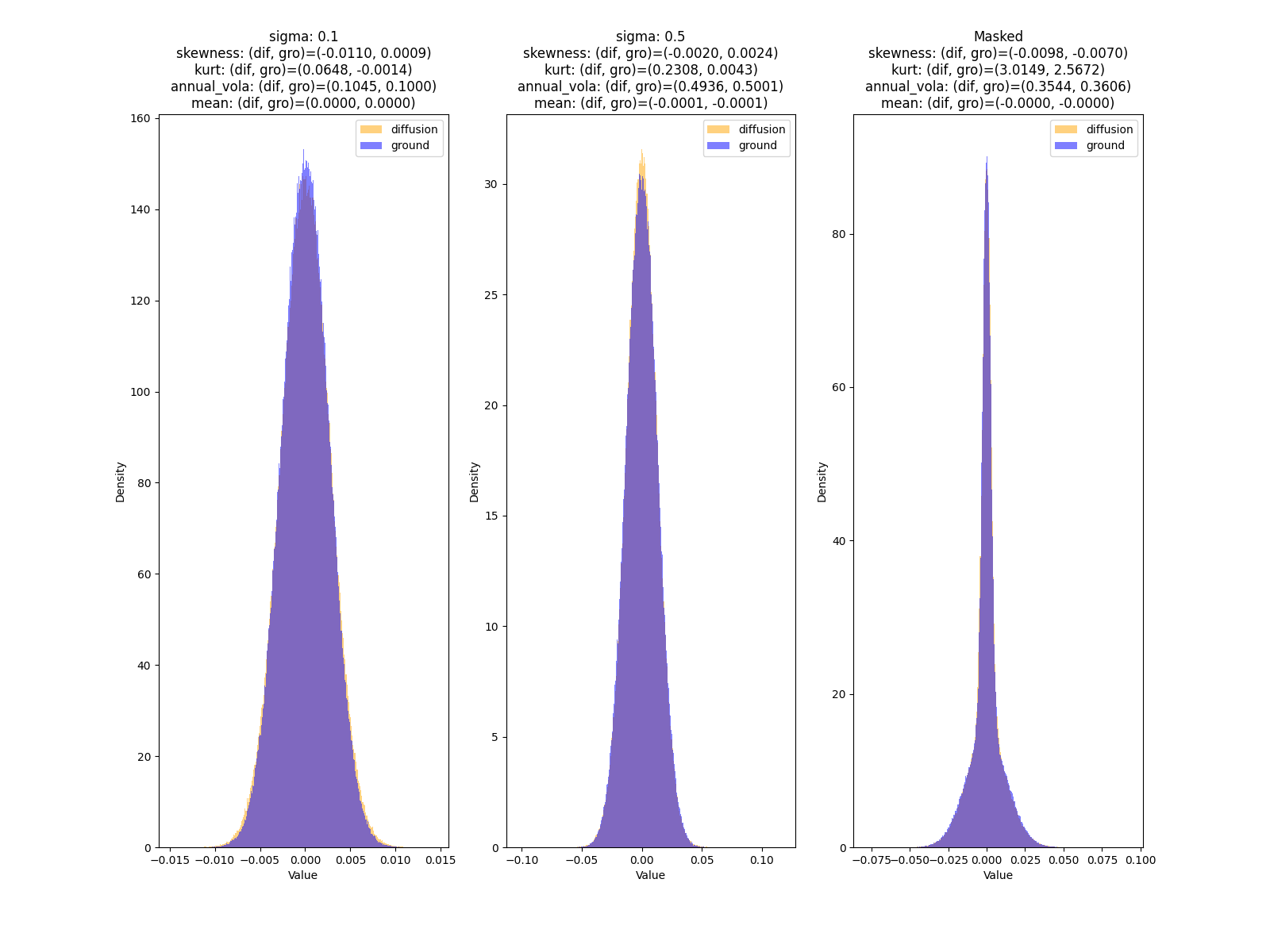
こちらは、価格系列と対数リターン系列を、与える条件ごとにGround Truthと生成データで比較したものです。いずれの場合も似たような振動具合が見られ、定性的には分布再現が成功していると考えられます。
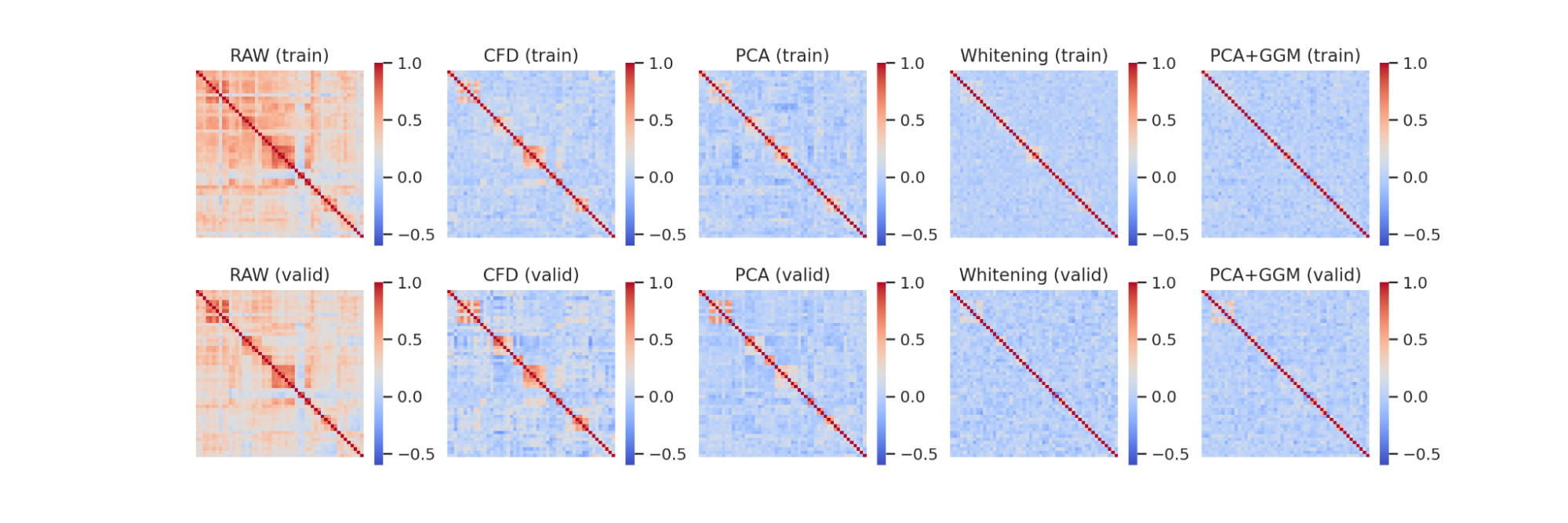
評価2: ヒストグラムによる対数リターンの分布
こちらに示しているのは、対数リターンの分布を示したものです。
以降、Maskedとは、条件をマスクすることを示します。
これを見ると、3つそれぞれでGround Truthの分布を捉えられていることがわかります。
| \(\sigma=0.1\) | 平均 | 年率ボラ | 歪度 | 尖度 |
| Ground Truth | 0.000 | 0.100 | 0.001 | -0.001 |
| Diffusion | 0.000 | 0.105 | -0.011 | 0.065 |
| \(\sigma=0.5\) | 平均 | 年率ボラ | 歪度 | 尖度 |
| Ground Truth | 0.000 | 0.500 | 0.002 | 0.004 |
| Diffusion | 0.000 | 0.494 | -0.002 | 0.231 |
| \(\sigma\): Masked | 平均 | 年率ボラ | 歪度 | 尖度 |
| Ground Truth | 0.000 | 0.361 | -0.007 | 2.567 |
| Diffusion | 0.000 | 0.354 | -0.010 | 3.015 |
表1. 対数リターンの統計量の比較。上からsigma: 0.1, sigma: 0.5, sigma: Masked。
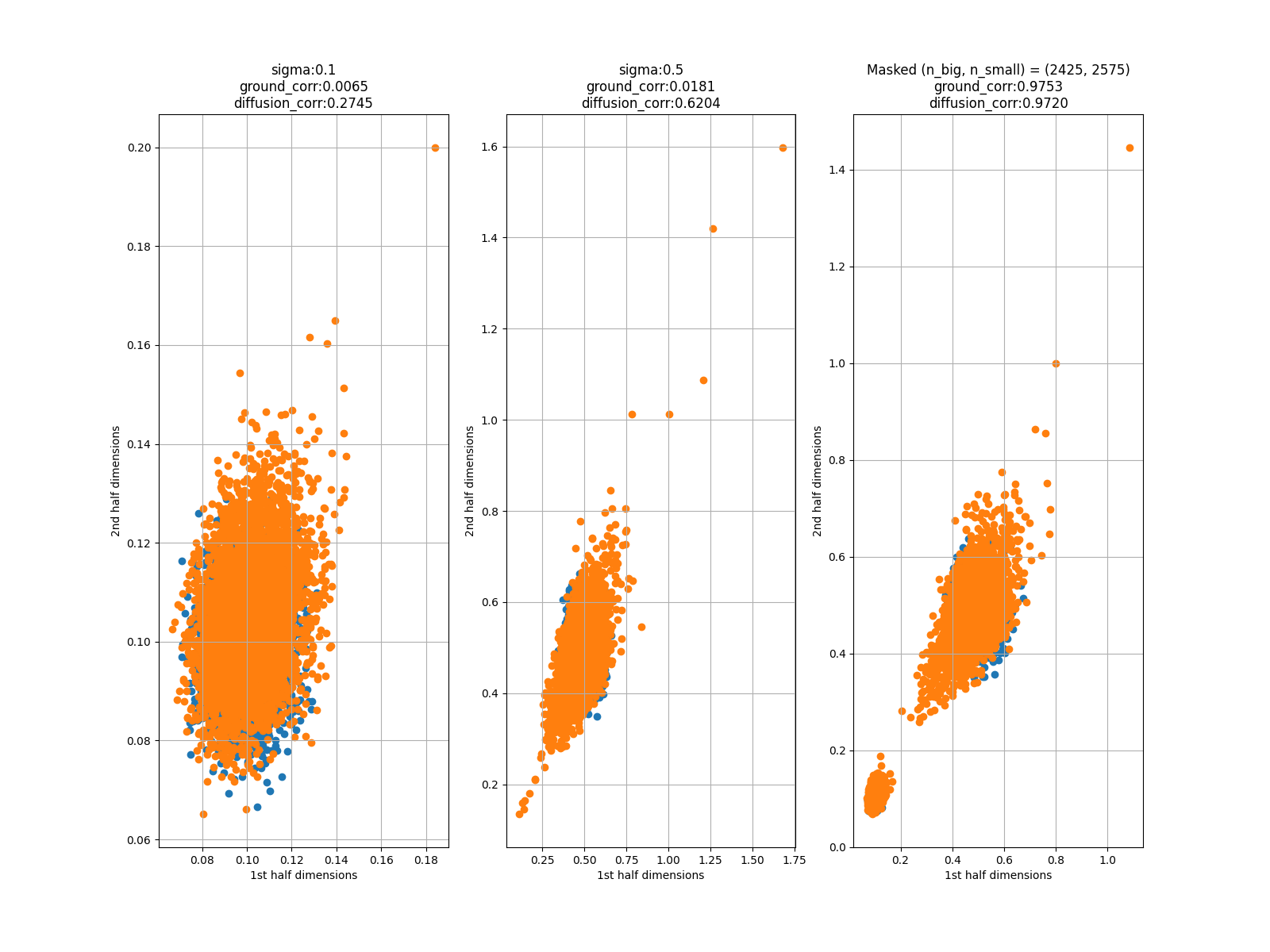
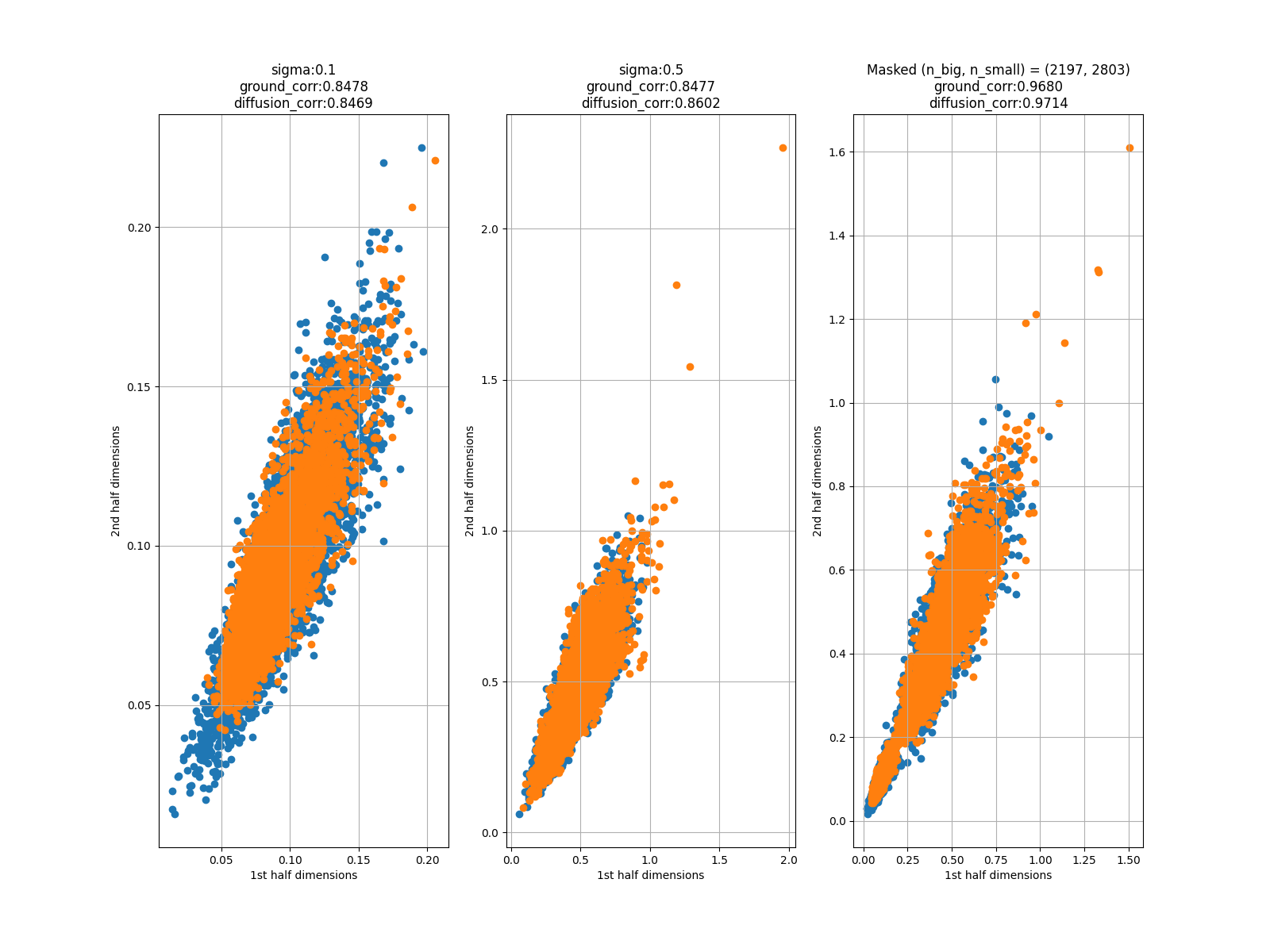
評価3: ボラティリティ変化の散布図
こちらに示したのは、前半64データポイントでのボラティリティを横軸に、後半64データポイントでのボラティリティを縦軸にプロットしたものです。青がGround Truth、オレンジが生成データです。
これを見ると、外れ値はあるものの、大まかな範囲を捉えていることがわかります。
\(\sigma=0.5\)、条件をマスクした時に右肩上がりの分布になってしまっています。
これは、\(\sigma=0.1\)の時の分布に引っ張られているからだと考えられ、学習回数を増やすことで改善される可能性があります。
Hestonプロセス
今回は、ボラティリティの標準偏差である\(\sigma\)を条件付けの対象としました。
\(\sigma\)の意味がBrownianプロセスと異なることに注意してください。
Brownianプロセスと同様の方法で評価した結果を以下に示します。
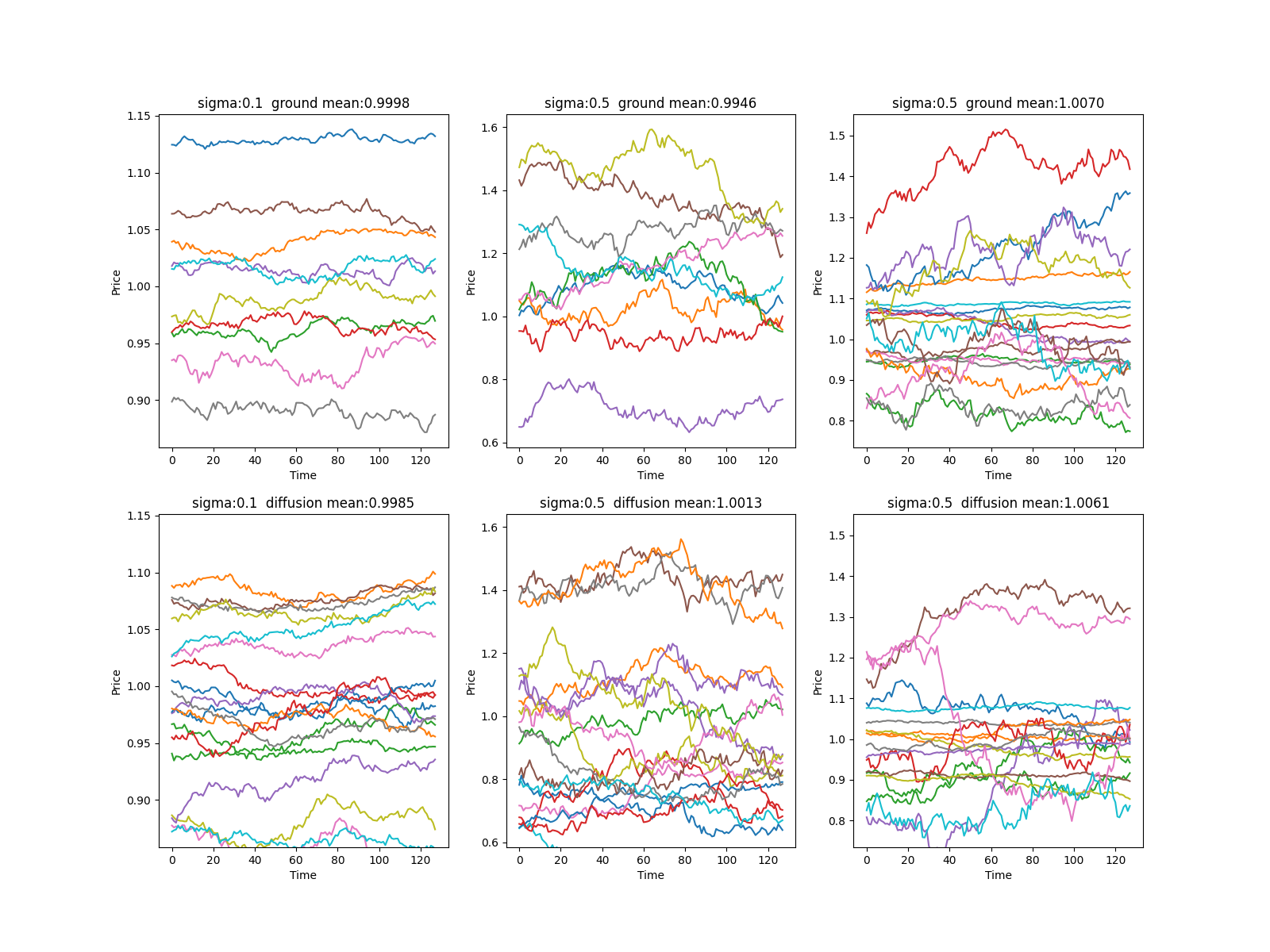
評価1: 価格系列と対数リターン系列の定性的な比較
価格系列におけるGround Truthと生成データの比較です。
こちらも似たような振動具合で、定性的に良い分布再現ができています。
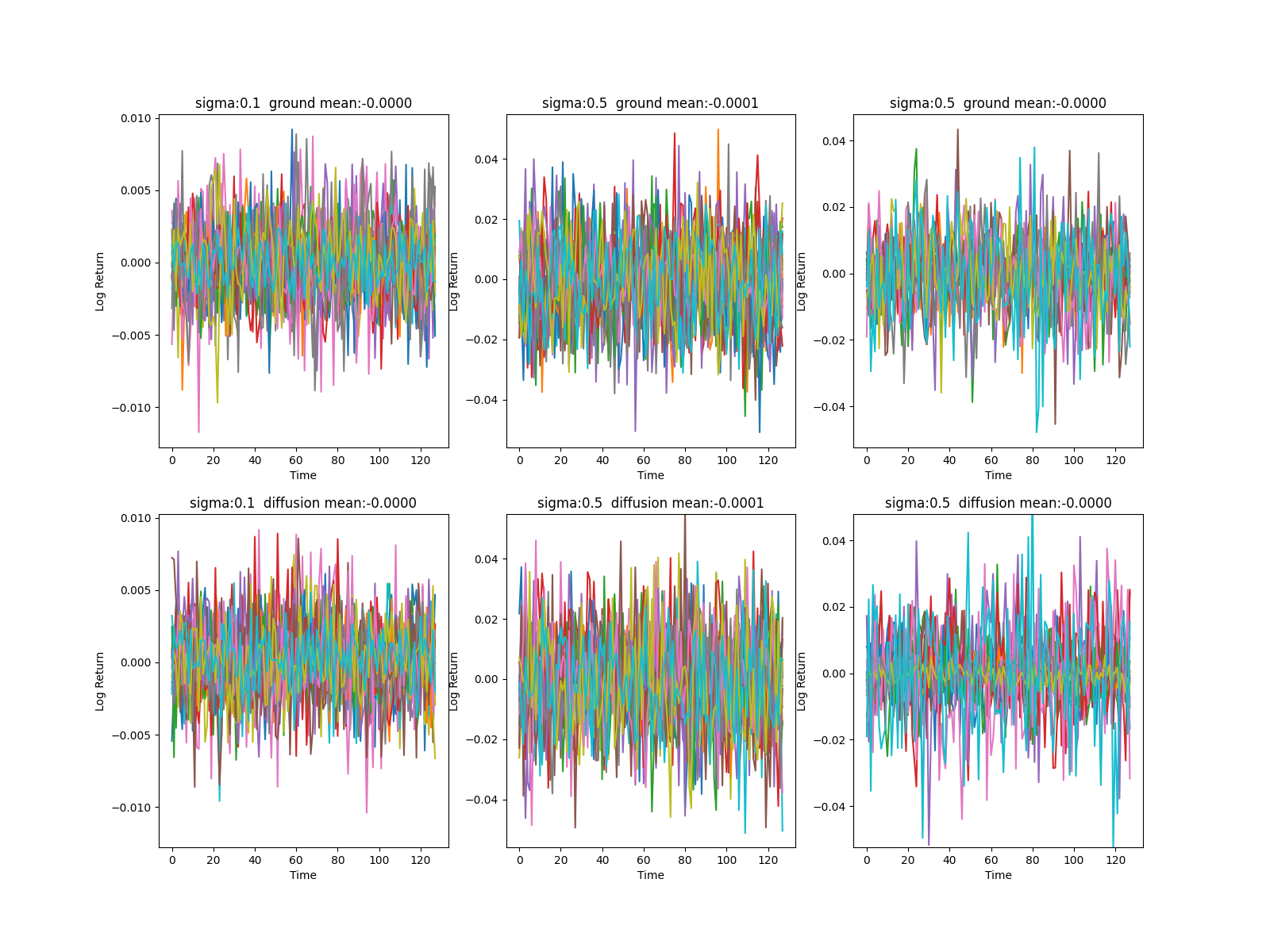
評価2: ヒストグラムによる対数リターンの分布
Hestonプロセスにおける対数リターンの分布を示します。
Brownianプロセスのときと同様、分布再現に成功していると考えられます。
\(\sigma=0.1\)の時はGround Truthより尖ってしまっています。
これは、もう1つの条件パターンが\(\sigma=0.5\)であるため、Ground Truthよりもsigmaが大きい方向にずれたと考えられます。
| \(\sigma=0.1\) | 平均 | 年率ボラ | 歪度 | 尖度 |
| Ground Truth | 0.000 | 0.101 | -0.019 | 0.810 |
| Diffusion | 0.000 | 0.091 | -0.033 | 0.768 |
| \(\sigma=0.5\) | 平均 | 年率ボラ | 歪度 | 尖度 |
| Ground Truth | 0.000 | 0.500 | -0.027 | 0.781 |
| Diffusion | 0.000 | 0.506 | -0.048 | 1.133 |
| \(\sigma\): Masked | 平均 | 年率ボラ | 歪度 | 尖度 |
| Ground Truth | 0.000 | 0.356 | -0.060 | 4.140 |
| Diffusion | 0.000 | 0.354 | -0.073 | 4.947 |
表2. 対数リターンの統計量の比較。上からsigma: 0.1, sigma: 0.5, sigma: Masked。
評価3: ボラティリティ変化の散布図
Brownianプロセスと同様、前半64データポイントでのボラティリティを横軸に、後半64データポイントでのボラティリティを縦軸にプロットしたものです。
青がGround Truth、オレンジが生成データです。
いずれの場合も、概ねGround Truthの分布を再現できていることがわかります。
$\sigma=0.1$では、外れ値は発生していませんが、標準偏差が小さい左下の部分は生成できていません。これは、学習用データ中にこのような部分のデータが相対的に少なく、モデルが学習できなかったためだと考えられます。
結論・今後の展望
拡散モデルを用いた金融時系列(Brownianプロセス・Hestonプロセス)の生成に取り組みました。
生成された時系列を取引戦略の評価に用いるという実応用の観点から、プロセスを特性付けるパラメータで条件付けし、それを反映したデータが生成できるかを定性的・定量的に複数の評価指標から確認しました。
その結果、いずれの場合でも分布再現に成功しました。
今後の展望として、実データを用いて同様の実験を行い、実用化を目指す方向性が考えられます。
感想
「拡散モデルをしっかり触ってみたい!」「金融の時系列に興味がある!」という中で本テーマに取り組むことを決めました。
私に未熟な部分も多くあり、ここまで多くの壁がありましたが、最後に綺麗な結果が得られて非常に達成感を感じています。
7週間という短い期間の中、毎日が学びの連続でした。
交流してくれたインターン生、快適な環境を提供してくださった社員の皆様、アドバイスいただいた金融チームの方々、特にメンターの平野さん・imosさん、ありがとうございました!