Blog
この記事は先日 arXiv に投稿した論文 “Efficient Crystal Structure Prediction Using Genetic Algorithm and Universal Neural Network Potential” https://arxiv.org/abs/2503.21201 に関するブログ記事です。
はじめに
この論文では PFCC が提供する Matlantisᵀᴹ の基盤技術であり、PFN が開発する汎用ニューラルネットワークポテンシャル(Neural Network Potential, NNP)の PFP を活用して結晶構造予測(Crystal Structure Prediction, CSP)を行う手法の提案を行いました。特に候補構造のサンプリングに工夫を行い、広いパラメータ空間を効率的に探索する工夫がなされています。本研究の成果である CSP アルゴリズムは PFCC が提供する Matlantis 上で利用が可能になる予定です。
ある元素系内で安定な結晶構造を特定することは材料探索において重要なタスクの一つです。ある元素の組み合わせでできる全ての化合物のうち、安定な構造の形成エネルギーを組成比の関数としてプロットした図1のような図は相図と呼ばれ、合成したい材料の安定性や合成方法を検討する上で重要な前提条件となります 。相図を原子シミュレーションによって探索する結晶構造予測は材料探索における代表的な問題設定の一つですが、密度汎関数理論(Density Functional Theory, DFT)計算の計算コストが高いために用途が限られてきました。特に組成を変化させながら探索を行い相図全体を計算により再現したり、系の中に存在する新しい結晶構造候補を網羅的に探索したりすることは容易ではありませんでした。
NNP の進歩により原子シミュレーションの計算コストが大幅に削減されましたが、NNP が対応する元素数が限られていたり、十分な精度で結晶のエネルギーを推論できなかったりするため、 CSP に実用的に活用することが難しいという課題がありました。しかし近年、元素によらずに様々な材料に適用可能な汎用 NNPが登場し、精度の改善も進んでいるためCSPを軽量な計算コストで行う道が開かれつつあります。材料探索においては、3元素以上の多元素系での探索や元素の置換、微量添加を考慮する必要があり、汎用NNPとの相性が良いと考えられます。さらに、結晶構造の安定性を評価するためには数十 meV/atom 程度の精度で形成エネルギーを正確に計算する必要があり、近年の汎用NNPの精度向上によりこの要件も満たせるようになってきました。こうした進歩・発展により、「多元素を対象とする」、「組成を変化させながら探索する」といった特性を持つ CSPを汎用NNPを用いて取り組めるようになった一方で、これまでは問題にならなかった組成空間での探索効率や並列実行効率向上の必要性といったアルゴリズム上・実装上の課題に直面することになったため、解決方法を模索しました。
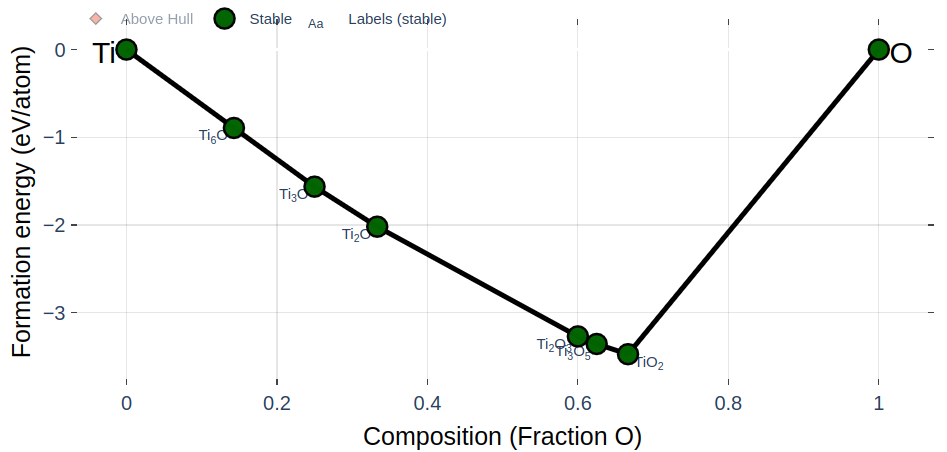
図1. Ti-O 系の相図の例
論文では、以下の特徴を持った新しい CSP 手法を提案しました。
- 汎用 NNP である PFP を用いて高速に結晶構造のエネルギーを評価できる。
- 遺伝的アルゴリズム(Genetic Algorithm, GA)を用い、多目的最適化手法を応用した選択手法によって探索履歴を有効活用した効率的なサンプリングができる。
- 特定の組成比のみを探索するのではなく、組成比が可変な遺伝操作を行うことで相図全体を探索することができる。
また実装上の工夫として、探索を管理するバックエンドに Optuna を用いることで高度に並列化した探索が可能となっています。Optuna は PFN が中心となって開発するオープンソースのブラックボックス最適化のフレームワークであり、本研究は PFN 社内のチーム間連携の結果として化学のドメイン知識と最適化技術を組み合わせた成果でもあります。
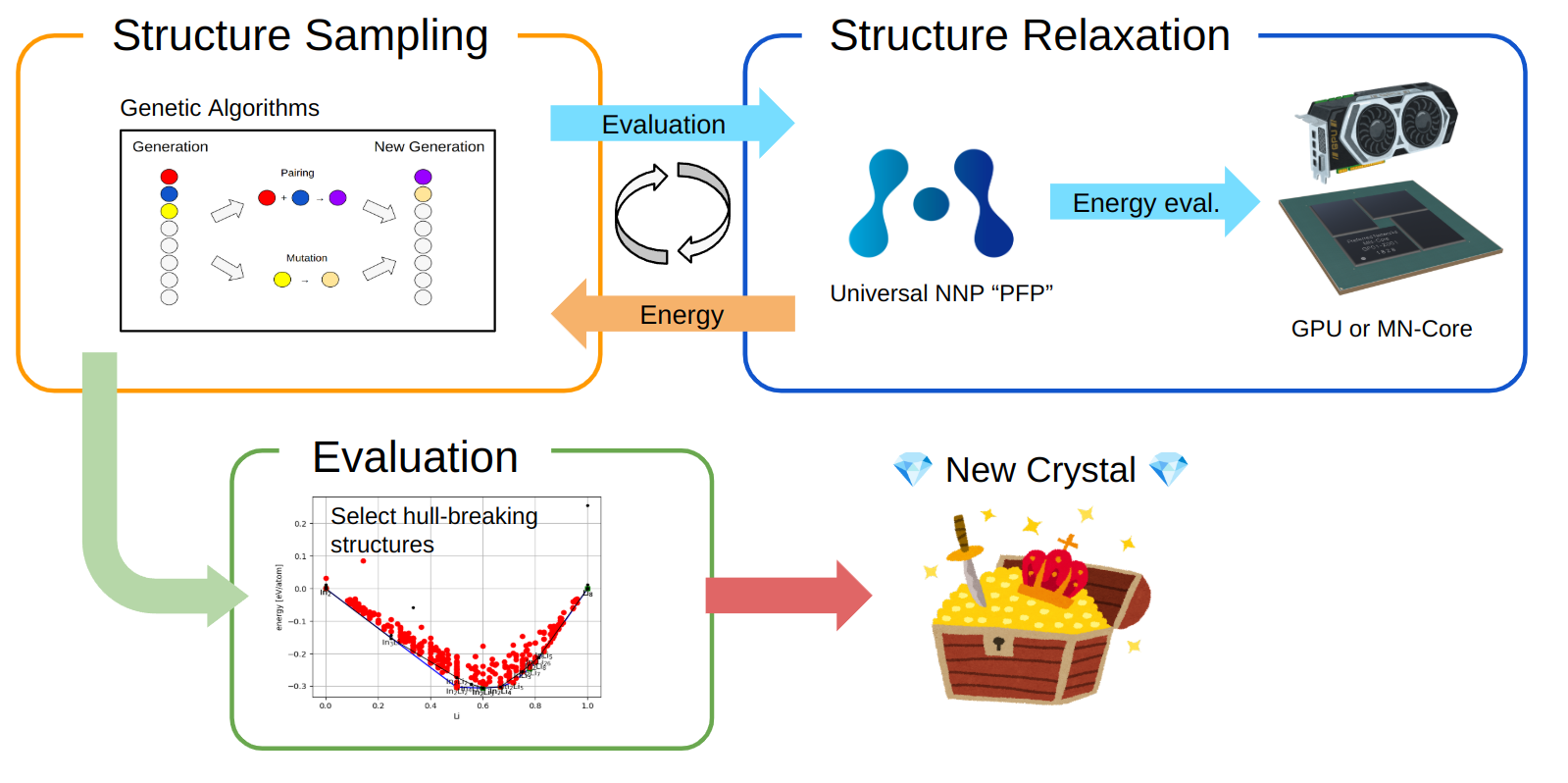
図2. CSP 探索の模式図
図2に CSP 探索の全体像を示しました。 CSP の探索は候補構造をサンプリングする Structure Sampling と構造緩和を行い近傍の安定点のエネルギーを評価する Structure Relaxation を繰り返すことで進めていきます。Structure Relaxation に関しては PFP を用いることで高速化が行われており、本論文では主に Structure Sampling の部分に関してサンプリング方法を高度化して PFP による高速化を活かすことができる CSP 手法を提案します。
次章では提案手法の Structure Sampling に関して解説します。
提案手法
結晶構造を決定するには、繰り返し単位である格子形状の情報、その中に含まれる原子の種類及び位置のパラメータを決定する必要があり、格子内の原子数によっては100次元以上の高次元パラメータ空間になります。このような高次元空間では探索問題を解くことが難しくなりますが、CSP では GA [1] を含めた様々な手法を用いて研究が行われてきました。また、結晶構造が持つ対称性に注目することで探索空間を削減する手法も研究されています[2]。本研究では GA を用いた探索手法を発展させました。GA は、生物の進化過程を模倣した最適化アルゴリズムの一種です。 複数の候補解からなる集団に対して選択と遺伝操作(交叉、突然変異など)の操作を繰り返すことで、より良い解を探索します。論文では選択と遺伝操作双方に関して提案を行いました。
相図を作成することを目標とした CSP では、エネルギーと組成の空間における様々な組成でより安定な構造を見つけることを目的とします(図3左)。これは数学的には凸包(convex hull, 点をすべて包含する最小の凸集合)を最大化することに対応します。この凸包の最大化を目的とした探索は、多目的最適化のパレートフロントの探索(図3右)と類似した問題設定となります。本論文ではこの類似性に着目して、多目的最適化をGAで行う際の選択アルゴリズムである NSGA-III(Elitist Non-dominated Sorting Genetic Algorithm III)[3] を CSP に応用しました。NSGA-III は多次元パラメータ空間の中で多様性を保って個体を選択できるように設計されており、これにより各世代の個体の多様性を担保します。
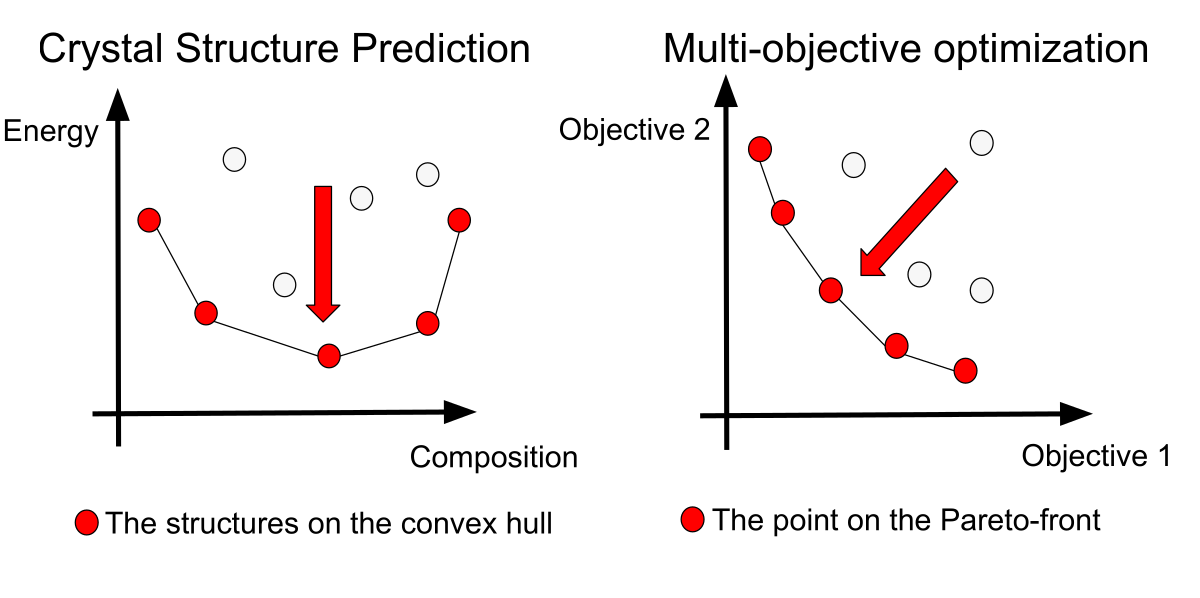
図3. CSP と多目的最適化の類似性
次に遺伝操作の拡張を行います。GA では有望な個体2つを用いた交叉や、一つの個体に変化を加える突然変異を問題設定に合わせて定義し、次の世代の個体をサンプリングしていきます。GA を用いた CSP では2つの結晶構造の一部を張り合わせる交叉や、一つの結晶構造の一部の元素を変更したり、原子位置をランダムに変化させたり入れ替えたりする突然変異が用いられます。ここで、今回の問題設定では組成をできるだけ連続的にサンプリングしたいですが、そのためには単位格子中の原子数を可変にする必要があります。これは単位格子中の原子数を固定した場合、例えば Ti-O 系で単位格子中の原子数が10個の場合に実現できる Ti の組成比は 0.1 刻みで 0.0, 0.1, 0.2, … 1.0 の構造しかサンプリングできず、TiO2 のような組成を探索することができないためです。本研究では単位格子中の原子数が変化することを許容するように交叉や突然変異を拡張しました。また、空孔を持つ構造をサンプリングするために親個体に存在する原子をランダムに削除するような突然変異も導入しました。
実験と結果
提案手法の有効性を検証するために 3, 4, 5, 8 元素系において提案手法とランダム生成の性能を比較します。また、Materials Project(MP)データベースに掲載されているデータとの比較も行います。比較に用いたランダム生成手法には PyXtal [2] を用いました。PyXtal では結晶構造にみられる対称性を考慮した生成が可能なため、ナイーブなランダム生成手法より性能が高いことが想定されます。定量的性能比較には凸包の超体積を用いました。これは図3左のような2元素系の場合は赤い点が囲む面積であり、これが大きいほど探索アルゴリズムの性能が高いと言えます。
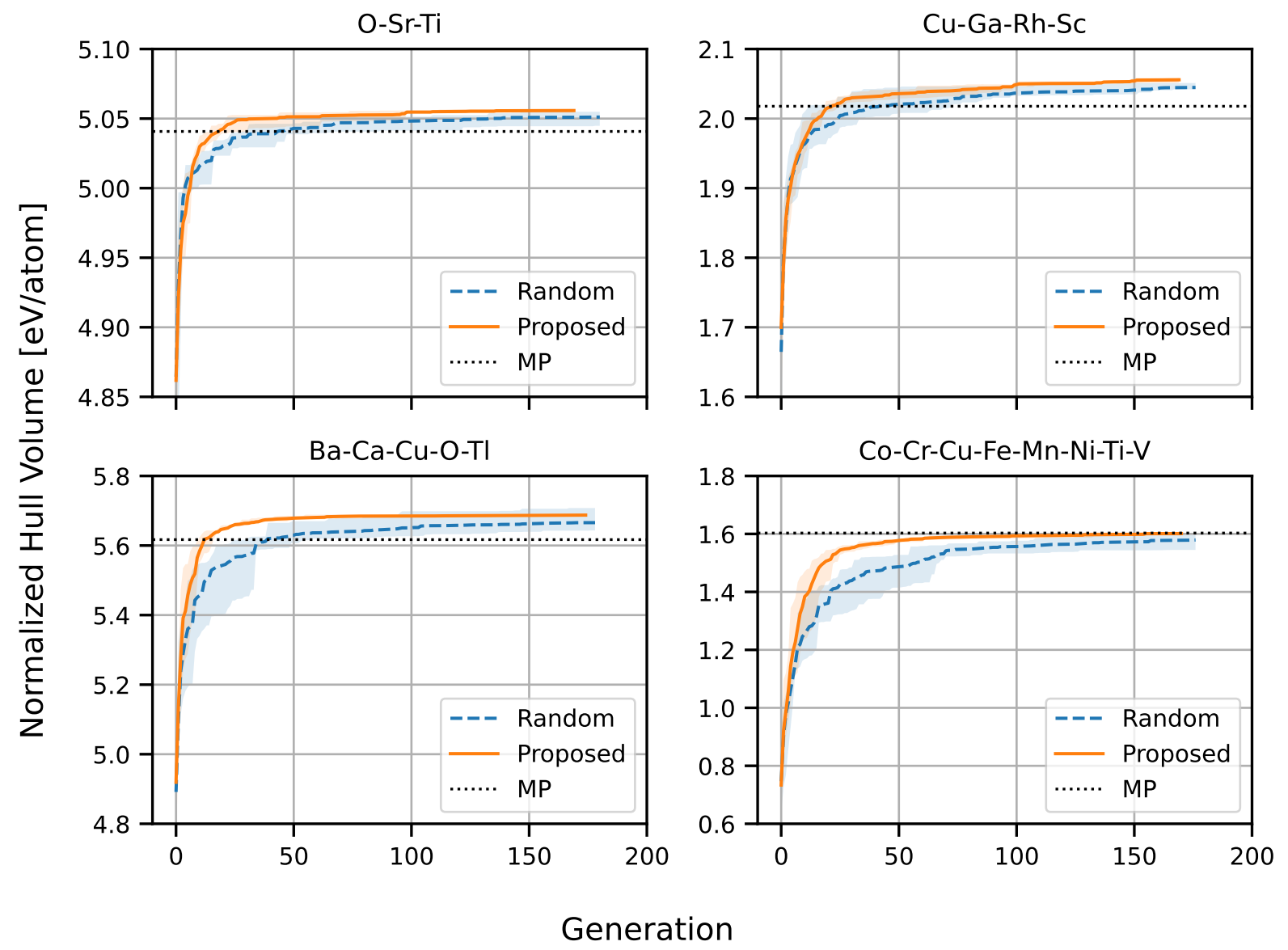
図4. 凸包超体積の探索履歴
図4 は 3, 4, 5, 8 元素系において凸包超体積が GA の世代ごとにどう変化するかを示したものです。この実験において1世代あたりの個体数は 250 であり、一度の探索で5万個の結晶構造をサンプリングして評価しています。オレンジ色の実線が提案手法を示しており、青破線で示したランダム生成よりも最終世代における性能は高く、探索中も概ねランダム生成よりも優れていることがわかります。また、探索初期の立ち上がり速度も優れている場合が多いことがわかります。これにより我々の CSP 手法はより少ない試行回数でより大きな凸包を達成できることが示されました。点線で示した MP との比較では8元素系ではわずかに劣っているものの、他の系では上回り、データベースにはない新しい構造を発見する能力が十分にあることがわかります。
次に、提案手法が更に実用途に近い形で新しい結晶材料候補を発見できるのかを検証します。ここでは GA の初期集団にMPデータベースの結晶構造を追加し、探索によって更に安定な結晶を発見できるかを評価します。
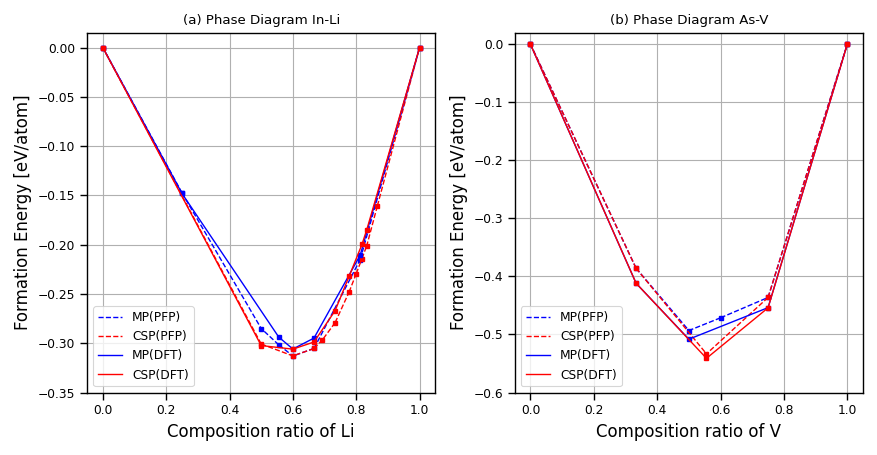
図5. 探索により新しい結晶候補が見つかった系の相図
図5は、提案手法を用いた探索の結果として新しい結晶候補が見つかった系の一部について、探索結果および MP データベースの相図をPFP と DFT でエネルギー値を評価した場合についてまとめています。この図からわかることはいくつかありますが、まずは赤実線(CSP, DFT)と青実線(MP, DFT)を比較します。これにより MP のデータベースの相図に対して CSP の探索結果がよりエネルギーが低く安定な結晶構造候補を発見できているかどうかを見ることが出来ます。図を見ると赤実線の方が下側にあり、実際に新しい結晶構造候補を発見できていることがわかります。これにより凸包を押し広げてより凸包面積も大きくなっていることもわかります。この探索を含めて論文中で報告した新しい結晶構造候補の一部を図6に示しています。これらの構造は直感的にも尤もらしい構造になっています。論文では4つの系で発見された28個の新しい安定構造候補に関して報告しています。
次に、赤線で示されているCSP探索結果について、破線(CSP, PFP)と実線(CSP, DFT)の結果を比較してみたいと思います。これらを比較することで、PFP のエネルギー推論精度に関して考察することが出来ます。PFP は DFT のエネルギーを推論するように学習していますが、データベースに載っていない未知の構造についてどの程度の推論精度が出るかは自明ではありません。赤破線と赤実線を比較すると、0.01 eV/atom 程度の誤差でエネルギーの推論ができていることがわかります。また、凸包の形状も概ね一致しており、エネルギーの順序が誤差により大きく入れ替わってしまうようなことは見られませんでした。ここから PFP は CSP を行うのに概ね十分な程度の推論精度があることがわかります。
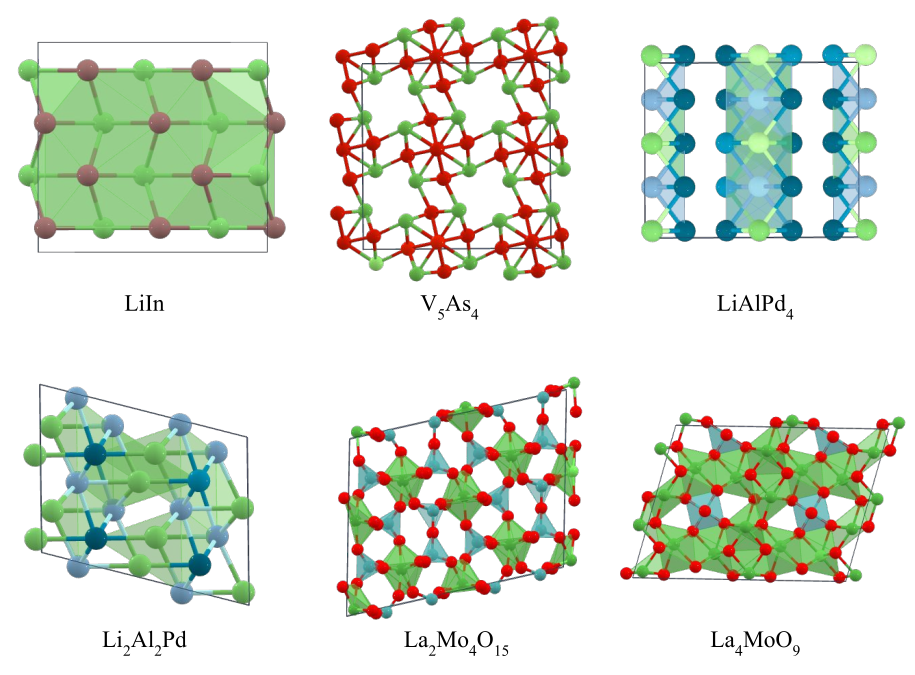
図6. 発見された結晶構造の可視化
まとめ
本論文では、PFN が開発する汎用 NNP である PFP と GA を組み合わせた新しい CSP 手法を提案しました。提案手法は、多目的最適化におけるパレートフロントの探索と凸包更新の類似性に着想を得ており、結晶構造の多様性を維持しながら、効率的に凸包超体積を最大化するように設計されています。実験の結果、提案手法は対称性を考慮したランダム構造生成よりいくつかの観点で優れており、より少ない試行回数でより大きな凸包を達成できることが示されました。実際の材料探索用途を模した実験でも相図を更新する新しい安定構造候補を複数発見することを示し、実用性を実証しました。
これらの結果より我々の CSP アルゴリズムが、データベースにあまり情報が無いような元素系であってもその相図や安定構造を探索することができ、材料設計において強力なツールとなる可能性を示唆しています。本研究の成果である CSP アルゴリズムは、 PFCC が提供する Matlantis 上で利用が可能になる予定です。このように PFN では 基盤技術である PFP を活用しつつ、幅広い技術を組み合わせて PFP だけでは解けない現実の問題に対してアプローチしています。
最後に
PFN で化学関係のプロジェクトを担当する Materials チームでは一緒に PFP の改善や Matlantis の機能拡張をするエンジニア、リサーチャーを随時募集しています。また、今回の社内のチーム間連携のように、PFN では最適化やコンピュータ・サイエンスのスキルを化学やその他分野に応用することもできます。本記事を通してご興味を持っていただけた方はぜひ下記ページや PFN website の Careers ページより詳細をご確認ください。
Material Discovery Researcher / リサーチャー(材料)
注記: PFP v6は、産業技術総合研究所の人工知能橋渡しクラウド(AI Bridging Cloud Infrastructure、ABCI)とPreferred Networksの自社スーパーコンピューターを使用して開発されました。
[1]: A. R. Oganov and C. W. Glass, J. Chem. Phys. 124, 244704 (2006) https://pubs.aip.org/aip/jcp/article-abstract/124/24/244704/567275/Crystal-structure-prediction-using-ab-initio?redirectedFrom=fulltext , https://arxiv.org/abs/0911.3186
[2]: S. Fredericks, K. Parrish, D. Sayre, and Q. Zhu, Comput. Phys. Commun. 261, 107810 (2021). https://www.sciencedirect.com/science/article/abs/pii/S0010465520304057?via%3Dihub https://arxiv.org/abs/1911.11123, https://arxiv.org/abs/1911.11123
[3]: K. Deb and H. Jain, IEEE Trans. Evol. Comput. 18, 577 (2014)., https://doi.org/10.1109/TEVC.2013.2281535