Blog
本記事は、2023年インターンシップで勤務された羽飼雅也さんによる寄稿です。実装はこちらに公開されています。テーマ内容のスライドは以下にアップロードされています。
背景
化学現象の解明や新規材料・デバイスの開発に向けたシミュレーションでは密度汎関数理論(Density Functional Theory, DFT)がよく使われています。しかし大規模な系の計算や創薬・材料開発分野における多数の候補分子のスクリーニング、長時間の第一原理分子動力学(Ab Initio Molecular Dynamics, AIMD)などにおいてはDFTの計算時間が問題となってしまいます。そこで、DFTで計算されたエネルギー、フォースをNeural Network(NN)で学習するNeural Network Potential(NNP)[1]が近年盛んに研究されています。NNPを用いることでDFTの計算精度を維持しつつ、高速に計算することができ、大規模・長時間のシミュレーションに活路を見出しています。Matlantis™内部でもNNPが用いられており[2]、その有用性が確かめられています。
DFT計算および従来のNNPで予測できるエネルギーは基底状態(\(S_0\))と呼ばれる、分子の最も安定な電子状態のエネルギーです。外場のない条件では分子は基底状態で存在していますが、光や熱などを加えると基底状態よりもエネルギーの高い励起状態と呼ばれる電子状態になります。光が関与する科学現象や光と分子の相互作用を利用した材料・デバイスは、この励起状態と密接に関わります。例えば光合成や動物の視覚は光と分子の相互作用が鍵となっています。また、太陽電池や有機EL、蛍光プローブなどの光が関与するデバイス・技術にも励起状態の性質が利用されています。これらの現象の理解やデバイスの向上のためには、励起状態のシミュレーションが必要となります。
励起状態の計算には時間依存密度汎関数法(Time Dependent Density Functional Theory,TDDFT)[3]がよく用いられます。エネルギーの低い順に第一励起状態(\(S_1\))、第二励起状態(\(S_2\))と名付けられます。本記事では簡単のために、スピンは一重項のみを考えています。フランク-コンドンの原理[4]によると、光で励起され一時的にエネルギーの高い電子状態となった分子は、励起状態のPotential Energy Surface(PES)に従い、分子構造が緩和されます。その後、光を放射しながら基底状態に戻る蛍光過程を経ます。実際には、この過程以外にも光を放射せずに基底状態に戻る内部転換(Internal Conversion,IC)という過程や、スピン反転が起き三重項状態に変化する項間交差(Instersystem Crossing,ISC)なども存在します。また、吸収した光エネルギーが化学反応や結合の解離に用いられる場合もあります。このように複雑な励起状態の振る舞いを、コンピューターで適切にシミュレーションするためには、励起状態PESの正確な予測が必要となります。
そこで本インターンシップではTDDFTで計算された励起状態エネルギーとそのフォースをNNで学習し、複数の分子種に対応する励起状態NNPの開発を目指しました。先行研究[5-7]では、単一の分子もしくは類似した構造をもつ少数の分子種を学習し、長時間の励起状態MD計算や励起状態の性質予測に成功しています。しかし、幅広い元素・分子種に対応した汎用的な励起状態NNPは未だ開発されていないのが現状です。
手法
用いたNNPのベースラインモデルと学習に使ったデータセットについて説明します。続いて励起状態のエネルギーに関する示量性・示強性の性質を示し、それらを考慮した出力層・損失関数について説明します。詳細についてはスライドおよび参考文献を参照ください。
NNPベースラインモデル
NNPのベースラインモデルとしてMaterials 3-body Graph Network(M3GNet)[8]を用いました。
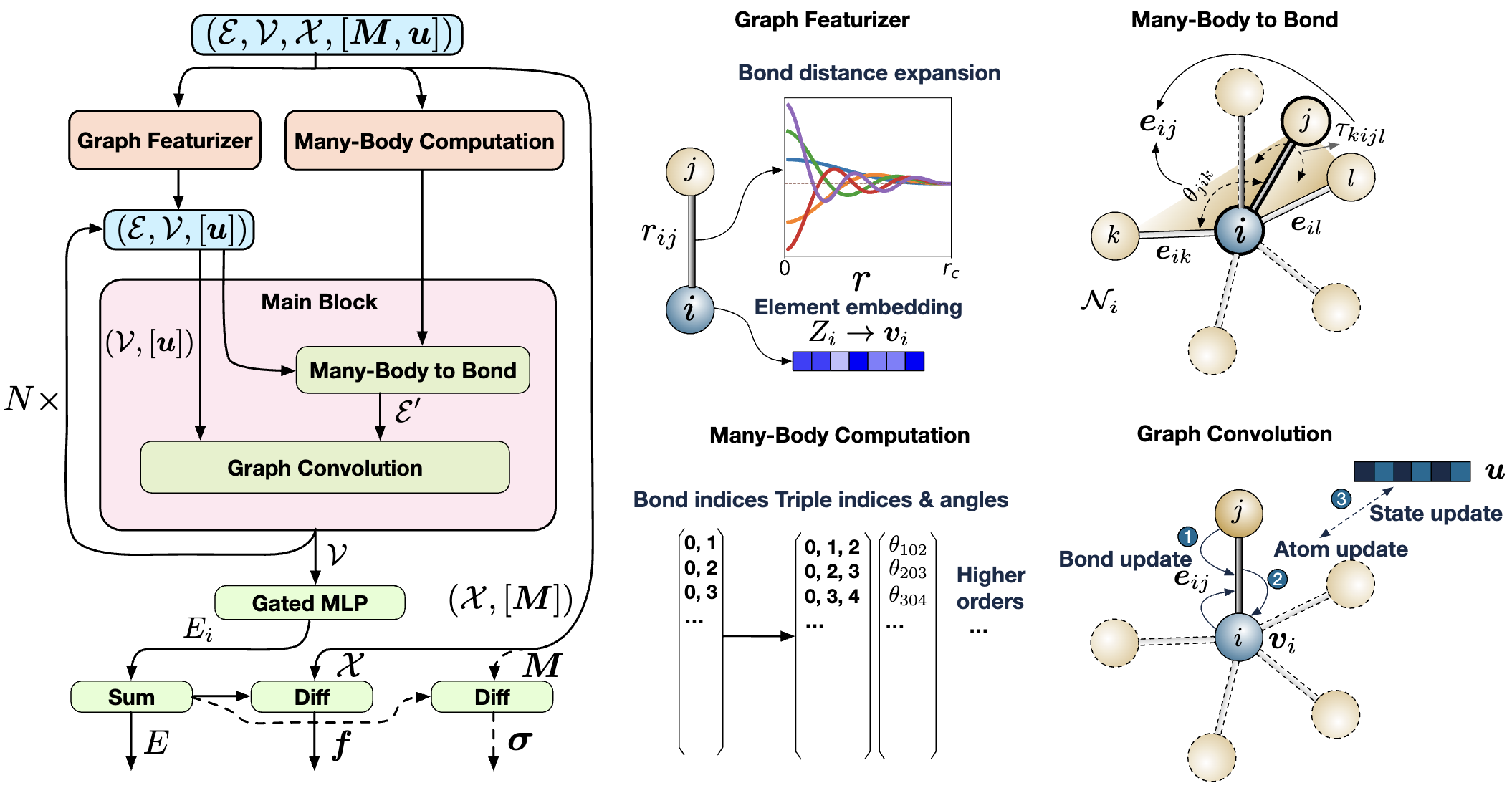
図1:M3GNetモデルの概要([8]より引用)
データセット
Gaussian16を用いてTDDFT PBE0/6-31G(d)の条件で励起状態のエネルギーとそのフォースを含むデータセットを作成しました。炭素数1 ~ 6個から成るアルカンデータセットとQM9データセット[10]を元に作成したQM5データセットを作成しました。まずそれぞれの分子種についてDFTを用いて基底状態\(S_0\)の構造最適化を行いました。その後TDDFTを用いて第一励起状態\(S_1\)の構造最適化を行い、平衡構造を得ました。(図2)
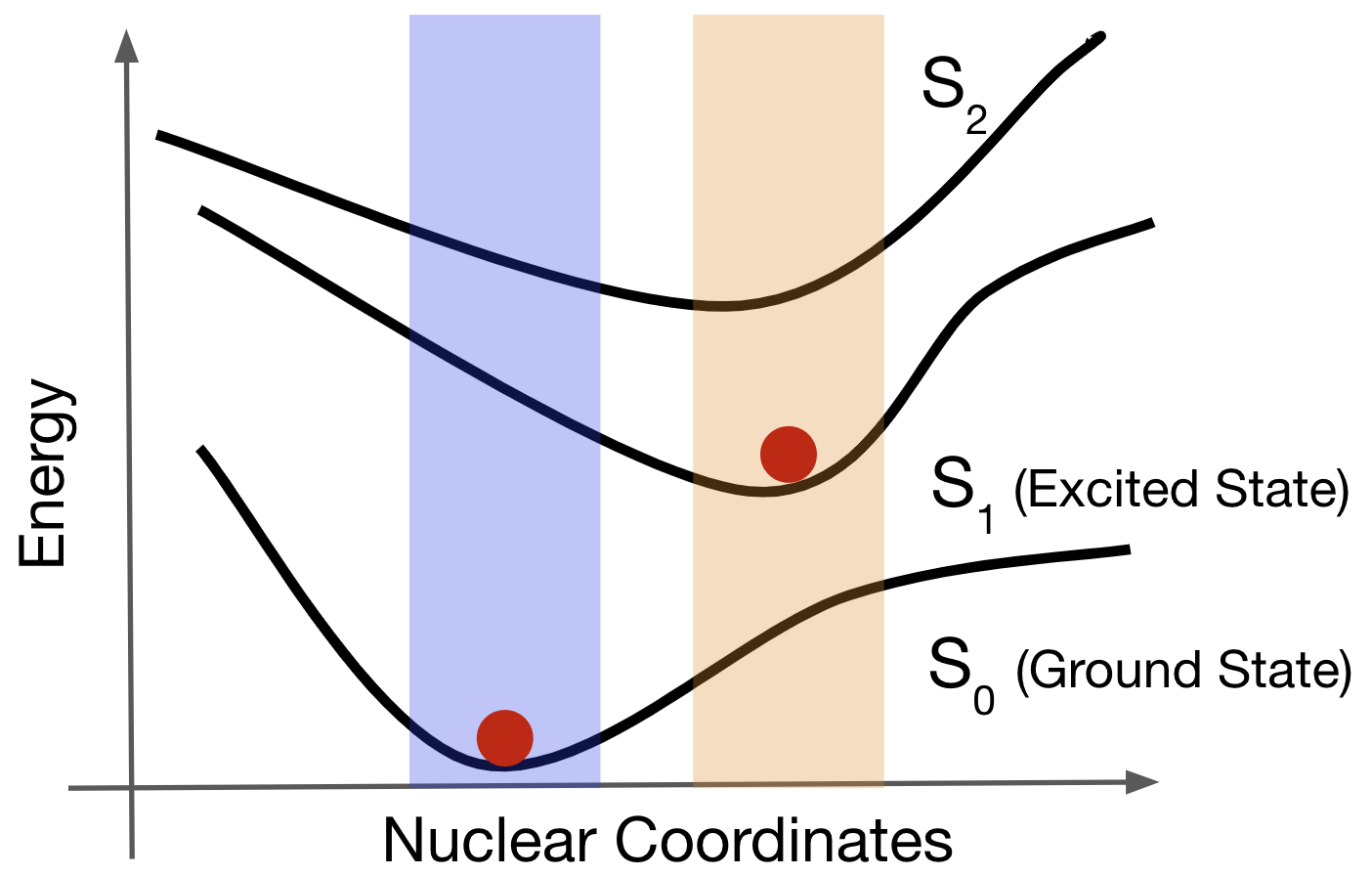
図2:基底状態PESと励起状態PESの模式図
それぞれの平衡構造は図2の赤点に相当します。それぞれの平衡構造を基にWigner sampling[11,12]を行い、PES上の平衡構造付近の構造をサンプリングしました。(図2中の青色・橙色の領域に相当します。)アルカンデータセットは炭素数1 ~ 6の直鎖アルカンの\(S_0\)平衡構造からそれぞれ200構造、炭素数5・6直鎖アルカンの\(S_1\)平衡構造からそれぞれ500構造、合計4,000構造から成ります。QM5データセットはQM9データセットからC,N,O,Fを最大5つ含む分子、合計178分子を抜き出し、それらの\(S_0\),\(S_1\)構造最適化を行いました。最終的に177個の\(S_0\)平衡構造と108個の\(S_1\)平衡構造が得られ、それぞれの平衡構造から200構造、合計57,000構造のサンプリングを行いました。TDDFT計算を用いた励起状態での構造最適化は難しく、69分子の\(S_1\)構造最適化に失敗しています。こちらに原因ついては、TDDFT計算では円錐交差(Conical Intersection, CI)付近の計算が不安定になること[13]、基底状態では安定分子として存在するが、励起状態では結合乖離してしまい局所最適構造が見つからないことなどが考えられます。また、最適化途中で分子が線形になるとGaussian 16がエラーで止まってしまうなどのプログラム上の問題もありました。Wigner samplingを用いて平衡構造からサンプリングした後、各構造で\(S_0\),\(S_1\),\(S_2\)のエネルギーとフォースを計算し、データセットを作成しました。同様の手順で炭素数7・8の直鎖アルカン(ヘプタン・オクタン)それぞれ100構造を含むデータセットを作成し、外挿性のテストとして用いました。
示量性・示強性
後で述べる励起状態エネルギーの出力層・損失関数の設計では、分子物性の原子数\(N_{\mathrm{atom}}\)に対する振る舞いに着目しています。ここではその導入として、示量性(extensive property)と示強性(intensive property)についてまとめています。
ここで分子Aと分子Bのある物性値について、その複合系であるA+Bの物性値はどのように変化するかを考えます。ここでは分子Aと分子Bは十分に離れており、相互作用しないと仮定します。基底状態のエネルギー\(E_g\)についてそれぞれのシュレディンガー方程式を考えます。
$$
H(A)|\Psi_{g}(A)\rangle=E_{g}(A)|\Psi_{g}(A)\rangle\\
H(B)|\Psi_{g}(B)\rangle=E_{g}(B)|\Psi_{g}(B)\rangle\\
$$
ここで複合系A+Bのハミルトニアンを\(H(A+B) = H(A)+H(B)\)とすると、複合系の基底状態波動関数と基底状態エネルギーは次のようになります。
$$
|\Psi_g(A+B)\rangle=|\Psi_g(A)\rangle \otimes |\Psi_g(B)\rangle\\
E_g(A+B) = E_g(A)+E_g(B)
$$
つまり、複合系A+Bの基底状態エネルギーは、分子Aと分子Bのそれぞれの基底状態エネルギーの和になります。このように物理量が系のサイズに対して線形でスケールすることを示量性と呼びます。
一方で励起状態エネルギー\(E_e\)については一般にこのような等式は成立しません。励起状態エネルギー\(E_e\)と基底状態エネルギー\(E_g\)の差分である励起エネルギー\(\Delta E\)を導入します。ここでは系Aの励起エネルギー\(\Delta E(A)\)は系Bの励起エネルギー\(\Delta E(B)\)よりも小さいと仮定します。複合系A+Bの励起エネルギーは次のようになります。
$$
E_e(A+B) = E_g(A+B)+\Delta E(A+B) \\
= E_g(A)+E_g(B) + \min(\Delta E(A),\Delta E(B)) \\
\neq E_e(A)+E_e(B)
$$
つまり系A+Bの励起エネルギーは分子Aと分子Bの励起エネルギーのうち小さいものと一致するため、励起状態のエネルギーについては示量性が成立しません。励起エネルギーは系の大きさに依存しない示強性の性質を持ちます。
Readout layer (出力層)
従来の基底状態のNNPのReadout layerを拡張したSum modelと、励起エネルギーの示強性を考慮したSoftmin modelを実装しました。
Sum modelでは基底状態・励起状態のエネルギー\(E^{S_0}\),\(E^{S_1}\)を各原子の寄与\(E_{i}\)の和として表します。
$$
E^{S_0} = \sum_{i=1}^{N_{\mathrm{atom}}} E_i^{S_0}\\
E^{S_1} = \sum_{i=1}^{N_{\mathrm{atom}}} E_i^{S_1}\\
E_{i}^{S_0} = \mathrm{Gated \;MLP} {}^{S_0}(\boldsymbol{v}_i)\\
E_{i}^{S_1} = \mathrm{Gated \;MLP} {}^{S_1}(\boldsymbol{v}_i)
$$
ここで\(\boldsymbol{v}_i\)は原子iのnode feature、\(\mathrm{Gated \;MLP}\)はゲート付き多層パーセプトロン(Gated Muilti-Layered Perceptron)です。
Softmin modelでは基底状態エネルギー\(E_{S_0}\)についてはSum modelと同じ形式ですが、励起状態エネルギー\(E_{S_1}\)を以下のように定式化します。
$$
E^{S_1} = E^{S_0} + \Delta E \\
=E^{S_0} + \sum_{i=1}^{N_{\mathrm{atom}}}\mathrm{Softmin}(E_{i}^{S_1})E_{i}^{S_1} \\
\mathrm{Softmin}(E_i) = \frac{e^{-E_i}}{\sum_{i=1}^{N_{\mathrm{atom}}} e^{-E_i}}
$$
励起状態エネルギーを基底状態エネルギーと励起エネルギーの和として考え、示強的な性質を持つ励起エネルギーに関しては原子数\(N_{\mathrm{atom}}\)に対してスケールしないようにSoftminの係数で重みづけしています。係数をSoftmin関数にすることで、複合系の第一励起エネルギーがそれぞれの系の最も低い第一励起エネルギーと一致するように設計しています。
Loss function (損失関数)
従来の基底状態NNPの損失関数を拡張した\(E^{S_1}\) Lossと励起エネルギー\(\Delta E\)を直接損失関数に含んだ\(\Delta E\) Lossの二種類を考えました。
\(E^{S_1}\) Lossでは次のように損失関数\(L\)を定義しました。
$$
L = \left| (E_{\mathrm{NNP}}^{S_{0}}-E^{S_{0}})/N_{\mathrm{atom}} \right|^2
+ |(E_{\mathrm{NNP}}^{S_{1}}-E^{S_{1}}))/N_{\mathrm{atom}}|^2
+ \cdots
$$
ここで\(E_{\mathrm{NNP}}^{S_0}\),\(E_{\mathrm{NNP}}^{S_1}\)はNNPのoutput、\(E^{S_0}\),\(E^{S_1}\)はDFT,TDDFTの計算結果です。第一項はM3GNetで用いられている損失関数であり、第二項は第一項を励起状態エネルギーへ拡張したものになります。フォースについても同様にLossを計算します。
\(\Delta E\) Lossでは、励起エネルギーが示強性であることを用いて次のように定式化します。
$$
L = |(E_{\mathrm{NNP}}^{S_{0}}-E^{S_{0}})/N_{\mathrm{atom}}|^2
+ |\Delta E_{\mathrm{NNP}}-\Delta E|^2
+ \cdots
$$
ここで励起エネルギー\(\Delta E_{\mathrm{NNP}}\)は\(\Delta E_{\mathrm{NNP}}=E_{\mathrm{NNP}}^{S_1}-E_{\mathrm{NNP}}^{S_0}\)とNNPで計算される量です。示量性である基底状態エネルギー\(E^{S_0}\)については原子数\(N_{\mathrm{atom}}\)で割った後の平均二乗誤差(Mean Squared Error, MSE)を考えていますが、示強性の励起エネルギー\(\Delta E\)は通常のMSEを損失関数として考えています。TDDFTの計算結果についても同様の計算を行っています。
結果と考察
アルカンデータセットでの学習
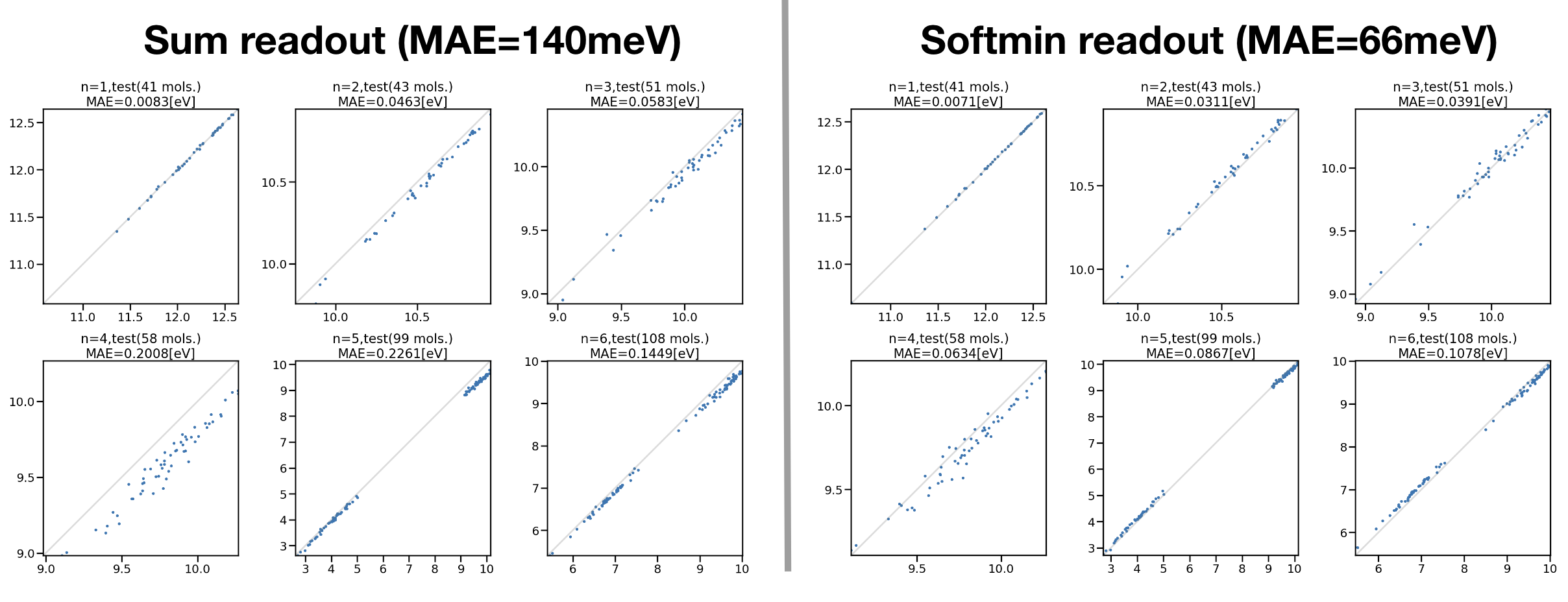
図3:アルカンデータセットで学習した励起状態NNPの励起エネルギーテスト
炭素数1 ~ 6のアルカンデータセットで学習した励起エネルギーのテスト結果が図3になります。図3左図がReadout layerにSum modelを用いた結果、図3右図がSoftmin modelを用いた結果になります。損失関数はどちらも\(E^{S_1}\) Lossを用いました。それぞれx軸がTDDFT計算の励起エネルギー、y軸がNNPの励起エネルギー予測値になります。6つのグラフはそれぞれ炭素数の異なる直鎖アルカンの計算結果になります。全ての分子種においてSoftmin modelを用いることでMAEが小さくなり、全体のMAE140 meVから66 meVへの改善という結果が得られました。
さらにReadout layerにSotmin model、Lossに\(\Delta E\) Lossを用いたテストデータのMAEは18 meVとなり、損失関数に励起エネルギーを直接取りこむことで精度の向上が確認されました。続いて学習済みのNNPを用いて、トレーニングデータに含まれていない炭素数7・8の直鎖アルカン(ヘプタン・オクタン)の外挿性能を確認しました。
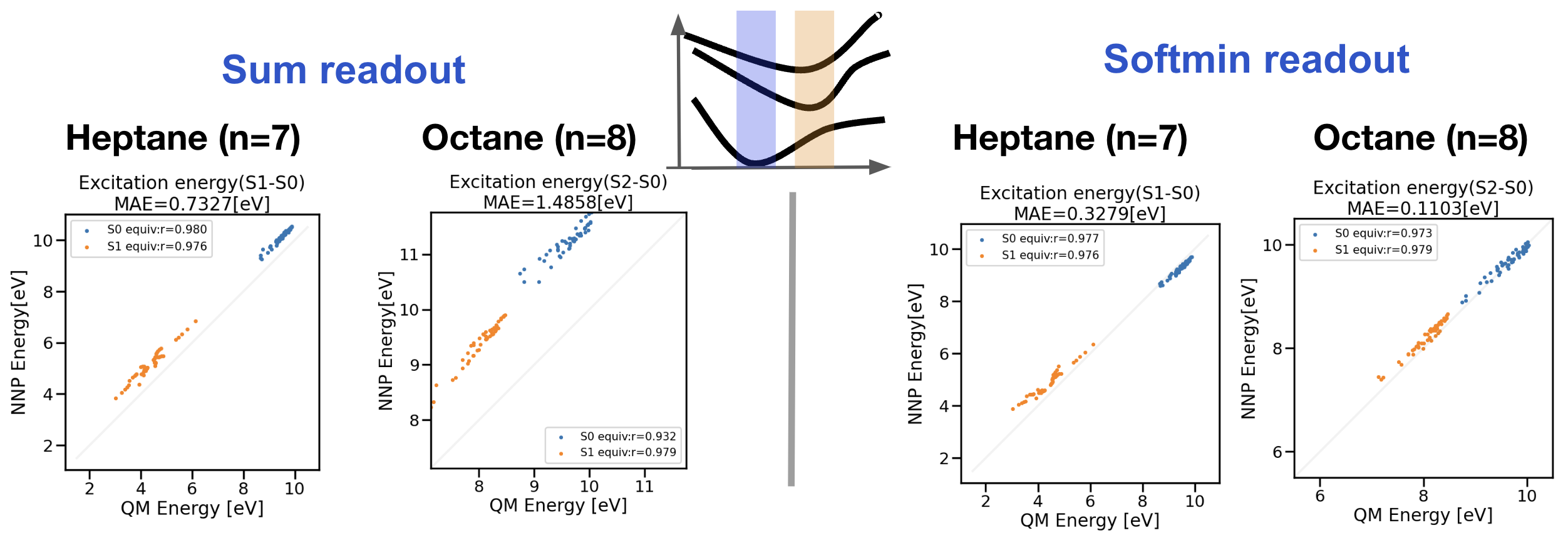
図4:アルカンデータセットで学習した励起状態NNPのヘプタン・オクタンの励起エネルギー外挿性テスト
図4左図がReadout layerにSum modelを用いた結果、図4右図がSoftmin modelを用いた結果になります。青色の点は\(S_0\)平衡構造を基にサンプリングされた構造での予測値、橙色の点は\(S_1\)平衡構造を基にサンプリングされた構造の予測値に対応します。(図4中央の模式図にそれぞれの色が対応しています。)Sum modelではヘプタンの励起エネルギーMAEが0.73 eVであるのに対し、Softmin modelでは0.33 eVと大きな改善が見られました。CASPT2/TZVPをレファレンスとしたTDDFT PBE0/TZVPのVertical Transition Energy(VTE)のMAEが0.24 eV[14]なので、Softmin modelはTDDFT自体がもつエラーと同程度のエラーで訓練データ外の分子を予測できたことになります。
さらにTDDFT計算結果とNNP予測値の相関が非常に高く、TDDFTの励起状態PESを正しく学習していることが示唆されます。そこで励起状態NNPを用いてヘプタンの\(S_1\)について構造最適化を行い、PESを正確に学習できているか検証しました。TDDFT計算で\(S_0\)平衡構造を初期構造として\(S_1\)構造最適化を行うと、中央のC-C-C結合角が113.5°から96.5°と狭まりました。励起状態NNPで同様に\(S_1\)構造最適化を行うと、中央のC-C-C結合角が97.8°となり、TDDFTで得られる構造と非常に似た構造が得られました。詳しくはスライド20ページに記載しています。
損失関数を\(\Delta E\)に変えて学習したモデルについてもヘプタン・オクタンの推論を行いましたが、大きな改善は見られませんでした。詳しくはスライドに記載しています。
QM5データセットでの学習
177分子種から構成されるQM5データセットについても励起状態NNPの学習を行い、NNPの表現力を確認しました。Readout layerにはSoftmin modelを、Lossには\(\Delta E\) Lossを用いました。
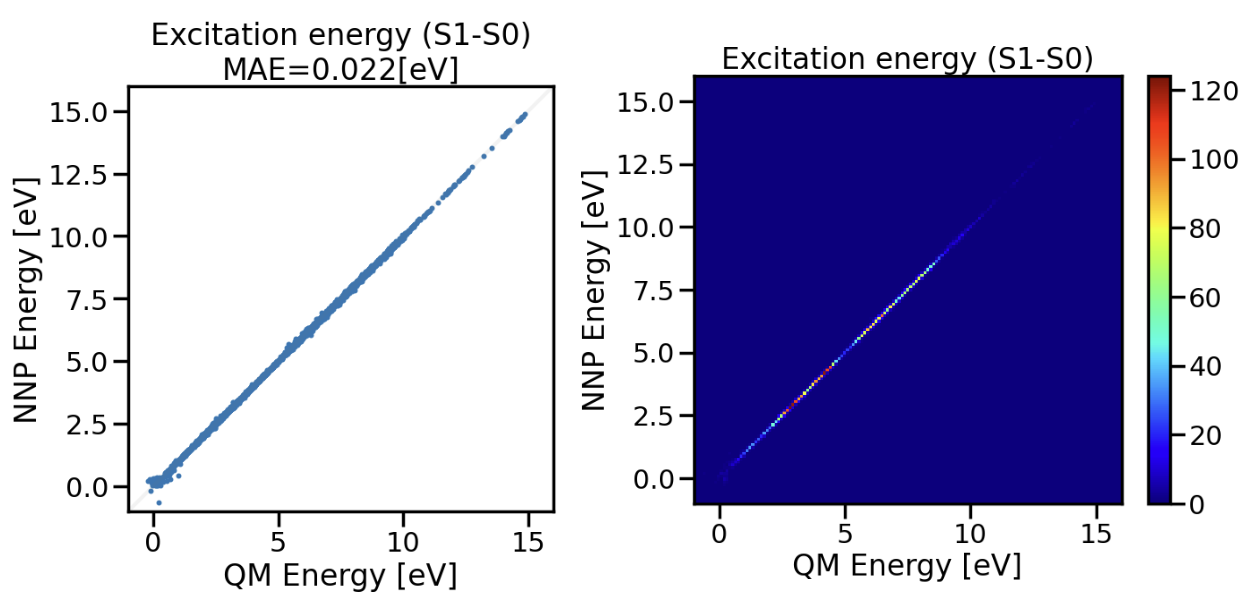
図5:QM5データセットで学習した励起状態NNPの励起エネルギーテスト。右図のカラーバーは分子の個数に対応。
テストデータの励起エネルギー予測結果は図5のようになりました。図5右図の二次元ヒストグラムのカラーバーは分子の個数に対応し、今回のテストデータでは4 ~ 6 eVに第一励起エネルギーをもつ分子が多いことがわかります。図5左図より励起エネルギーが0.01 ~ 15 eVという多様な励起特性をもつ分子群に対し、22 meVのMAEで予測できました。図5右図からサンプル数が少ない高エネルギー側も励起エネルギーを予測できました。
続いてQM5データセットで学習した励起状態NNPを用いて、ヘプタン・オクタン励起エネルギーの外挿性能を確かめました。
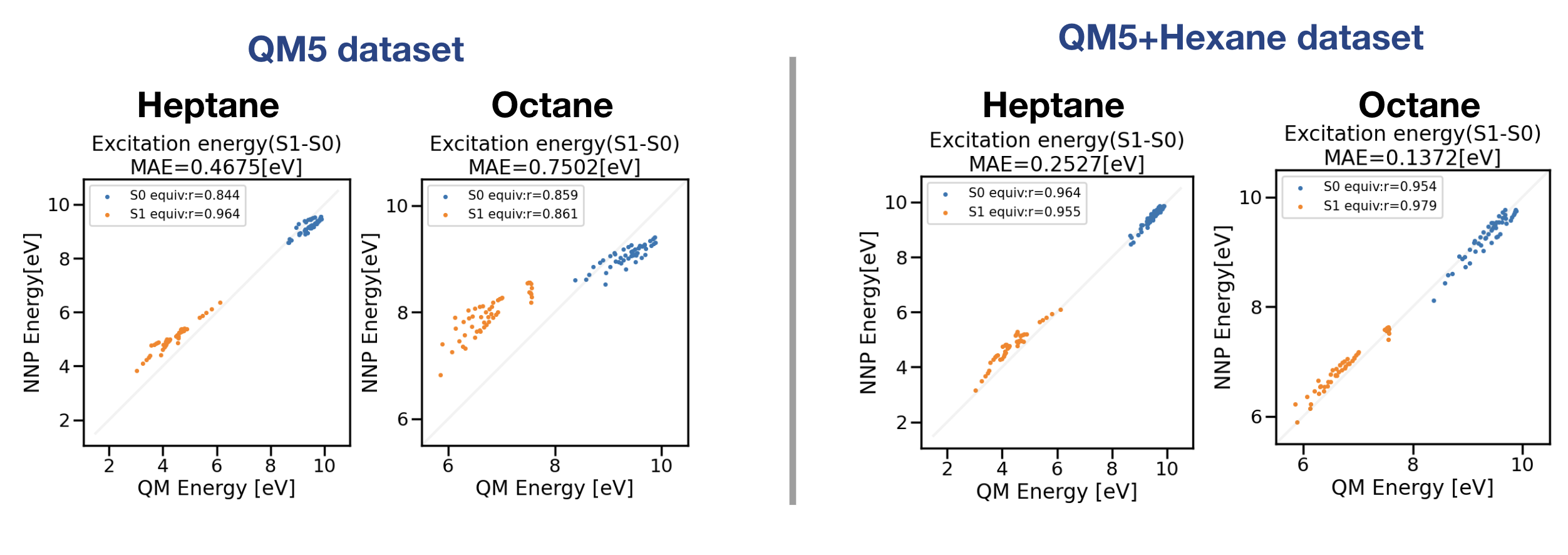
図6:QM5データセットもしくはQM5+ヘキサンデータセットで学習した励起状態NNPのヘプタン・オクタン外挿性テスト
図6左図はQM5データのみを学習したモデルの推論結果であり、ヘプタンのMAEは0.47 eV、オクタンのMAEは0.75 eVとアルカンデータセットの結果よりも精度の悪い結果が得られました。図6右図はアルカンデータセットからヘキサンのデータを抜き出し、QM5データセットに追加した訓練データで学習した結果になります。ヘプタン・オクタンのMAEはそれぞれ0.25 eV、0.14 eVとアルカンデータセットのNNPモデルと同程度の精度となりました。以上の結果から汎化性能を得るためにQM5データセットでは不十分であり、6つの炭素原子を含むデータを含めることで大幅にヘプタン・オクタンの推論性能が向上することが確認されました。
まとめ・謝辞
本インターンシップでは多様な分子種を含む励起状態データセットの作成と励起状態NNPの開発に取り組みました。基底状態エネルギーの示量性、励起エネルギーの示強性の性質を出力層や損失関数に反映することで、予測精度の向上が確認できました。また、訓練データに含まれていないヘプタンやオクタンの直鎖アルカンの励起エネルギーについては、TDDFT自体に含まれるエラーと同程度のエラーで推論できました。さらに学習した励起状態NNPを用いて、励起状態についての構造最適化にも成功しました。177分子種の基底状態と励起状態のエネルギー、フォースの学習を行い、テストデータを用いた検証ではTDDFT計算エラーよりも十分に小さいMAEで予測できました。
7週間という非常に短い期間ではありましたが、PFN社員の手厚いサポートのおかげで有意義な研究結果を残すことができたと思います。特にメンターの篠原さん、副メンターの澤田さんには毎日ディスカッションしていただき、今回のテーマをこのような形でまとめることができました。また材料探索チームの方々にも多くの質問やアドバイスをいただき、研究内容を深めることができました。本当にありがとうございました。
Reference
[1] J. Behler, M. Parrinello, Generalized Neural-Network Representation of High-Dimensional Potential-Energy Surfaces. Phys. Rev. Lett. 98, 146401 (2007).
[2] S. Takamoto, C. Shinagawa, D. Motoki, K. Nakago, W. Li, I. Kurata, T. Watanabe, Y. Yayama, H. Iriguchi, Y. Asano, T. Onodera, T. Ishii, T. Kudo, H. Ono, R. Sawada, R. Ishitani, M. Ong, T. Yamaguchi, T. Kataoka, A. Hayashi, N. Charoenphakdee, T. Ibuka, Towards universal neural network potential for material discovery applicable to arbitrary combination of 45 elements. Nat. Commun. 13, 1–11 (2022).
[3] M. Huix-Rotllant, N. Ferré, M. Barbatti, Time‐dependent density functional theory. Quantum Chemistry and Dynamics of Excited States (2020), pp. 13–46.
[5] J. Westermayr, P. Marquetand, Deep learning for UV absorption spectra with SchNarc: First steps toward transferability in chemical compound space. J. Chem. Phys. 153, 154112 (2020).
[6] J. Westermayr, M. Gastegger, P. Marquetand, Combining SchNet and SHARC: The SchNarc Machine Learning Approach for Excited-State Dynamics. J. Phys. Chem. Lett. 11, 3828–3834 (2020).
[7] G. G. Terrones, C. Duan, A. Nandy, H. J. Kulik, Low-cost machine learning prediction of excited state properties of iridium-centered phosphors. Chem. Sci. 14, 1419–1433 (2023).
[8] C. Chen, S. P. Ong, A universal graph deep learning interatomic potential for the periodic table. Nature Computational Science. 2, 718–728 (2022).
[9] https://github.com/materialsvirtuallab/matgl
[10] R. Ramakrishnan, P. O. Dral, M. Rupp, O. A. von Lilienfeld, Quantum chemistry structures and properties of 134 kilo molecules. Sci Data. 1, 140022 (2014).
[11] E. Wigner, On the Quantum Correction For Thermodynamic Equilibrium. Phys. Rev. 40, 749–759 (1932).
[12] M. Pinheiro Jr, S. Zhang, P. O. Dral, M. Barbatti, WS22 database, Wigner Sampling and geometry interpolation for configurationally diverse molecular datasets. Scientific Data. 10, 1–11 (2023).
[13] J. Westermayr, P. Marquetand, Machine Learning for Electronically Excited States of Molecules. Chem. Rev. 121, 9873–9926 (2021).
[14] A. D. Laurent, D. Jacquemin, TD-DFT benchmarks: A review. Int. J. Quantum Chem. 113, 2019–2039 (2013).