Blog
本記事は、2024年夏季インターンシッププログラムで勤務された樋野健太郎さんによる寄稿です。
有限温度系の拡散モデルによる分子構造生成
はじめに
こんにちは!2024年度夏季インターンシップに参加した京都大学の樋野健太郎です。
普段は、テンソルネットワークという道具をつかって量子多体系のシミュレーション手法を開発したりしています。
Preferred Networks (以下、PFN) の岡野原さんの著書[1]から拡散モデルに興味をもち、もともと興味のあった統計力学のPhysics-Informed Neural Network (PINN) [2]と組み合わせた、定量的な分子構造分布を再現する手法[3]を調査してみました。
この記事ではその結果と課題点について記しました。
なお、本内容の一部は昨年度インターンの貢献[4]を元にしております。
また一部を除いて、記法は参考文献[3]に基づきました。
なお、一部のソースコードはこちらで公開しています。
拡散モデルは定量性をもてるのか
データ学習型の拡散モデル
拡散モデルと聞いて皆さんはどのようなアプリケーションを思い浮かべますか?
私を含め多くの方は、Stable Diffusion[5]をはじめとする、画像生成モデルを思い浮かべると思います。
こういったモデルの多くは、訓練データ (画像) \(\mathbf{x}_0\)に小さなノイズを繰り返し付与していく順過程 ( \(t:0\to\tau\) )
\(\mathrm{d} \mathbf{x}_{t}=\frac{\beta_{t}}{2} \mathbf{x}_{t} \mathrm{d}t + \sqrt{\beta_{t}} \mathrm{d} \mathbf{W}_{t} \tag{1}\)
を考えます。
この順過程の確率微分方程式 (Stochastic differential equation; SDE) はWiener過程にしたがうノイズ項 \(\mathrm{d}\mathbf{W}_t\) があるため、高校の物理で習う運動方程式のように、時間 \(t\) を \(-t\) に置換しても等価な式にならず、軌跡の復元が困難です。
そこで、各ステップにおいて、ノイズ付与後のデータ \(\mathbf{x}_t\) からノイズ付与前のデータ \(\mathbf{x}_{t-\Delta t}\) を予測するようなモデルを構築します。
すると、完全なノイズデータ \(\mathbf{x}_{\tau}\) からスタートして、ノイズを取り除く逆過程 ( \(t:\tau\to 0\) )
\(\mathrm{d} \mathbf{x}_{t}=\frac{\beta_{t}}{2} \mathbf{x}_{t} \mathrm{d}t+\beta_{t} \nabla \log q\left(\mathbf{x}_{t},t\right) \mathrm{d}t+\sqrt{\beta_{t}} \mathrm{d} \mathbf{W}_{t} \tag{2} \)
を繰り返すことで、あたかも訓練データにあった様なデータ (画像) を復元 (生成) することを可能にしています。
ここで登場する、 \(\beta_t\) は時間ステップ幅のスケジュールに対応する定数です。
また、\(q(\mathbf{x}_t, t)\) は時刻 \(t\) までノイズを付与したあとの分布関数、その対数勾配 \(\mathbf{s}=\nabla \log q\) はスコアと呼ばれ、スコアベースモデルではこれをニューラルネットワークなどでモデル化します。
こうした拡散モデルは画像生成に限らず、分子や結晶の定性的な構造予測に対しても有望なアプローチとなりつつあります。
では、こうして生成される分子構造の分布を定量性を持って解釈できるでしょうか?
拡散モデルの一つであるスコアベースモデルの損失関数[6]を見つめてみましょう:
\(\sum_{i=1}^N \mathbb{E}_{\mathbf{x_0}\sim q(\mathbf{x})}\mathbb{E}_{\epsilon_i \sim\mathscr{N}(\mathbf{0}, \mathbf{I})} \left\| \sigma_i\mathbf{s}^\theta \left( \alpha_i\mathbf{x}_0+\sigma_i\epsilon_i, t_i \right) +\epsilon_i \right\|^2 \tag{3} \)
ここで、\(N\) は拡散過程のステップ数 (すなわち\(i\)は離散化時刻のインデックス) 、\(q(\mathbf{x})\) は教師データの分布、
スコア \(\mathbf{s}^{\theta}\) は \(\mathbf{x}\) と同じ次元をもつベクトル量で、ここに学習パラメータ \(\theta\) が含まれます。
また十分小さい正の実数 \(\beta_i=\beta_t\Delta t\;(i=1,2,\cdots,N)\) から \(\alpha_i=\prod_{j=1}^{i}\sqrt{1-\beta_j}\), \(\sigma_i=\sqrt{1-\alpha_i^2}\) が定まります。
この損失関数 (3) を”完璧”に訓練して、構造生成を行うと、ノイズから教師データを復元できます。
したがって、訓練データセットを物理的に意味のある分布 (例えば、温度 \(T=300\) KにおけるBoltzmann分布 \(\exp(-E(\mathbf{x})/k_{\mathrm{B}}T)\)) で統一しておき、完璧な訓練を行えば、理想的には物理的に意味のある分布からの定量的なサンプリングが達成できるわけです。
しかしながら、これが机上の空論であることは明らかでしょう。
完璧な訓練が困難であることは言うまでもなく、そもそも訓練データを採取する中で、レアイベントも含めて完璧なサンプリングを達成しておく必要があるからです。
さらには、もし完璧な訓練を達成してしまうと、教師データの分布をそのまま再現してしまうため、教師データに含まれている有限個の構造しか生成されず、物質探索で必要な外挿性能が保証されないというジレンマも抱えています。
物理方程式学習型の拡散モデル
さて、次の様な過程を考えてみます。:
1. \(q(\mathbf{x}, t=0)=\exp\left(-\frac{E(\mathbf{x})}{k_{\mathrm{B}}T}\right)\) を時刻 \(t=0\) の初期分布とする。
2. 時刻 \(t=0\to\tau\) まで、ある微分方程式にしたがって、確率密度関数 \(q(\mathbf{x}, t)\) を変化させる。
3. 終時刻 \(t=\tau\) では確率密度関数が、正規分布のようなサンプリングが容易な分布関数に収束する。
もし、この様な過程が達成できれば、この過程の逆向きを辿ることで、正規分布からサンプリングされた意味のないデータから、ある温度 \(T\) における分子構造を生成できそうです。
実際、拡散変数 \(\mathbf{x}_t\) を逆過程 (2) にしたがって \(t:\tau\to0\) へと遷移させることで、正規分布からサンプリングされた変数を、 \(t=0\) の分布にしたがうように結びつけることができます。この逆過程の個々の軌跡を積算した確率密度 \(q(\mathbf{x}, t)\) の時間変化は実は、次のFokker–Planck方程式に基づいています。
\(\frac{\partial}{\partial t} q = \nabla \cdot\left[ q\left[ \frac{\beta_{t}}{2} \mathbf{x}_{t} + \beta_{t}\nabla \log q \right] \right] – \frac{\beta_{t}}{2}\nabla\cdot(\nabla q)\)
この方程式の両辺を \(q\) で割り、 \(\nabla\) を作用させることで、スコア \(\mathbf{s}=\nabla\log q\) に関するFokker–Planck方程式が導出できます。
\(\frac{\partial\mathbf{s}}{\partial t} =\frac{\beta_{t}}{2}\nabla \left[ \mathbf{x}\cdot\mathbf{s} + |\mathbf{s}|^2 + \nabla\cdot\mathbf{s} \right]\)
この導出過程の行間に興味がある方は、Ito積分、Fokker–Planck方程式、後ろ向きKolmogorov方程式といったキーワードや参考文献[1,3]の付録を調べてみると良いです。
以上まとめると、1., 2.に従うという要請に関する損失関数を
\(\left\| \frac{\partial\mathbf{s}^\theta}{\partial t}-\frac{\beta_{t}}{2}\nabla\left[\mathbf{x}\cdot\mathbf{s}^\theta+ |\mathbf{s}^\theta|^2+ \nabla\cdot\mathbf{s}^\theta\right]\right\|^2+\left\|\mathbf{s}^\theta(t=0) + \frac{\nabla E(\mathbf{x})}{k_{\mathbf{B}}T}\right\|^2\tag{4}\)
として訓練することで、物理的に意味のある分布からのサンプリングが可能になりそうです。
ここで注意すべきは、物理方程式学習型の場合、拡散前の時刻 \(t=0\) における分子力場 \(-\nabla E\) を \(k_{\mathrm{B}}T\) で割ったもの (損失関数 (4) の第二項) から、再現すべき分布 \(q(\mathbf{x})\) の情報を獲得しているとう点です。つまり、データ学習型とは異なり、Boltzmann分布にしたがった理想的なデータセットを事前に容易しておく必要がありません。
定量性のある嬉しさ
PFNが開発している機械学習ポテンシャルPFP[7]に代表されるように、与えられた分子構造から、その構造に対応するエネルギーを定量的に予測することは可能になりつつあります。
こうしたエネルギー予測モデルは温度が0の環境を想定している一方で、身近な現象は300K付近の有限の温度で起きています。
有限温度における物性の予測をするには、分子動力学 (Molecular dynamics; MD) 法やマルコフ連鎖モンテカルロ (Markov-chain Monte-Carlo; MCMC) 法のようにエネルギー予測モデルを使った軌跡サンプリングをするのが一般的です。
しかしながら、こうした軌跡サンプリングは、時間に関する相関をなくすため、そしてレアイベントのサンプリングが必要であることに起因して、非常に長い時間の軌跡を計算せねばなりません。
拡散モデルによって、有限温度の分布にしたがう定量的な分子構造の生成が可能になれば、軌跡サンプリングよりも圧倒的に効率よく、自由エネルギーをはじめとする温度に依存する物性値を推定できるようになることが期待できます。
検証結果
2次元のモデル系 (混合ガウス分布)
先行研究[4]と同じ混合ガウス分布に対して損失関数 (4) を使った物理方程式学習型の拡散モデルを試してみました。
モデルは、残差接続のある多層パーセプトロンモデル (ResNet) を用いて、学習点は \([-4,4]^2\) から準モンテカルロ法で2048点をとりました。
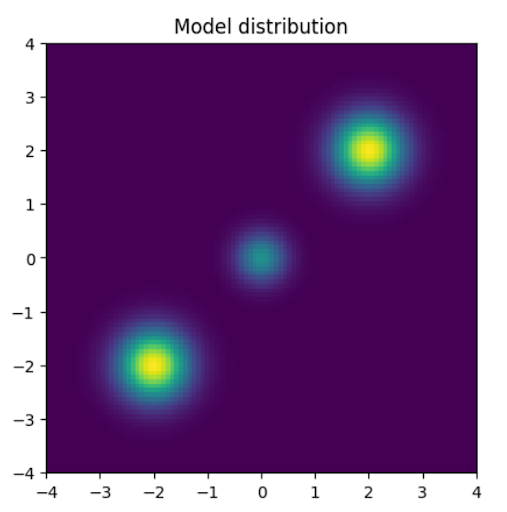
図1: 混合ガウス分布(t=0)
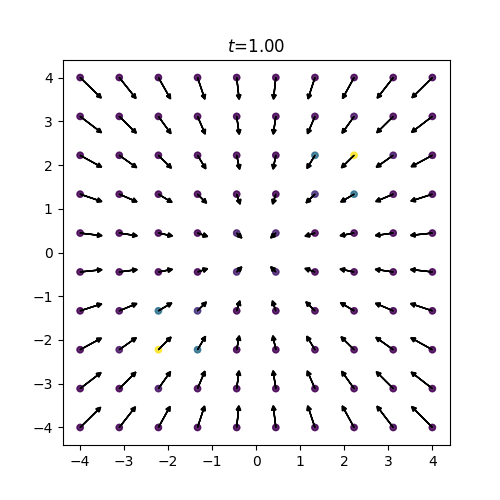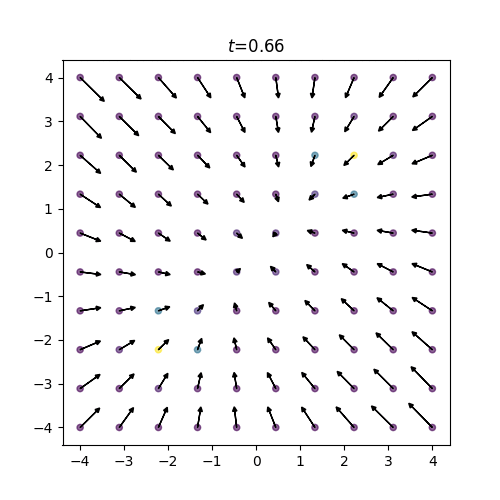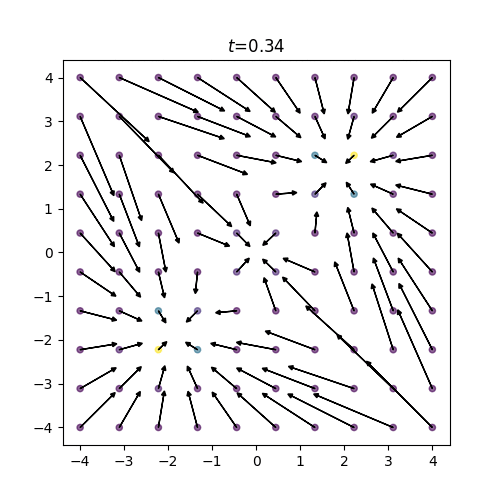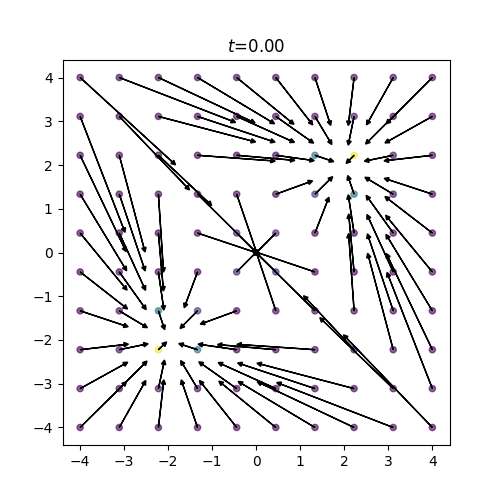
図2: 訓練スコア
終時刻 \(t=1(=\tau)\) において正規分布だったスコアが初期時刻 \(t=0\) の混合ガウス分布へと復元されていく様子がわかります。
訓練済みスコア関数 \(\mathbf{s}^\theta\) を使ったSDE
\(\mathbf{x}_N \sim \mathscr{N}(\mathbf{0}, \mathbf{I})\)
\(\mathbf{x}_{i-1} = \frac{1}{\sqrt{1-\beta_i}}\left(\mathbf{x}_{i} + \beta_i \mathbf{s}^{\theta}(\mathbf{x}_i, t_i)\right)+ \mathscr{N}(\mathbf{0}, \beta_i\mathbf{I})\)
で構造を生成したところ、以下の散布図のようになり、バランスよく混合ガウス分布からサンプリングできました。
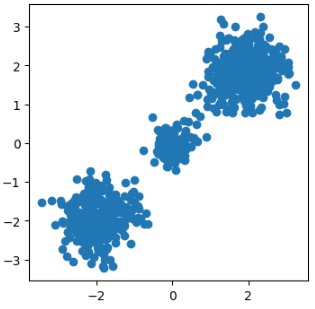
図3: SDEによりサンプリングされたデータ
また、常微分方程式 (Ordinary differential equation; ODE)
\(\mathrm{d} \mathbf{x}_t=-\frac{\beta_t}{2}\left[\mathbf{x}_t+\mathbf{s}^\theta\left(\mathbf{x}_t, t\right)\right] \mathrm{d} t\tag{5}\)
によって構造を生成をして、自由エネルギーの計算に必要な配置積分のモンテカルロ積分を以下の式で評価することも可能です。
\(Z=\int \mathrm{d}\mathbf{x} \exp\left(-\frac{E(\mathbf{x})}{k_{\mathbf{B}}T}\right)\simeq\mathbb{E}_{\mathbf{x}\sim q^{\theta}(\mathbf{x})}\frac{\exp\left(-\frac{E(\mathbf{x})}{k_{\mathbf{B}}T}\right)}{p^\theta(\mathbf{x})}\)
ここで、モンテカルロ積分の分母に現れる規格化された提案分布の確率密度 \(p^\theta(\mathbf{x})\propto q^\theta(\mathbf{x})\) は次の式で計算できます。
\(\log p^\theta\left(\mathbf{x}_0\right)=\log \mathscr{N}\left(\mathbf{x}_{t=\tau}^\theta\left(\mathbf{x}_0\right);\mathbf{0}, \mathbf{I}\right)-\int_0^{\tau} \frac{\beta_t}{2} \nabla \cdot \mathbf{s}^\theta\left(\mathbf{x}_{t}^\theta\left(\mathbf{x}_0\right), t\right) \mathrm{d} t-\frac{D}{2} \int_0^{\tau} \beta_t \mathrm{~d} t\)
ただし、\(\mathbf{x}^\theta_t(\mathbf{x_0})\) は \(\mathbf{x}_0\) に達するODEの軌跡で、 \(D\) は拡散変数 \(\mathbf{x}\) の次元です。
拡散モデルをつかったモンテカルロ積分の結果と、同じ点数を等間隔にとった数値積分の結果を以下のグラフに示します。
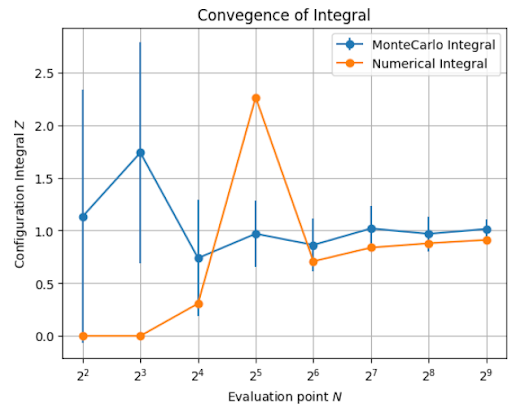
図4: 配置積分のモンテカルロ積分と数値積分による評価の比較
拡散モデルを使った方が少ない点数で厳密解1.0に収束しています。
このように、モンテカルロ積分の提案分布として拡散モデルを使うアプローチも有用です。
これは、分子系に限らず、金融シミュレーションなどにも使えそうですね。
さて、以上のように、簡単な混合ガウス分布では、物理方程式型学習によって、その学習済みモデルを使った構造生成や物性予測が可能であることがわかりました。
では、次に分子系で試してみます。
分子系 (水・グリシン)
分子系では、拡散前のスコア関数 \(\mathbf{s}^{\theta}(\mathbf{x}, t=0)\) (分子力場の定数倍) が以下の対称性を有します。
- 同一原子種の置換に対する対称性
- 系の平行移動に対する対称性
- 系の回転移動に対する対称性
- 系の鏡像移動に対する対称性
グラフ表現やアテンション機構を持ったニューラルネットワークは、こうした対称性を自動的に達成できる上に、異なる分子系に対しても同じアーキテクチャを適用できるという利点があります。
特に、今回は \(-\log q\) を学習するモデルではなく、\(\mathbf{s}=\nabla \log q\) を学習するスコアベースモデルであるため、系の回転に対する同変性 (系を回転させたときに、勾配ベクトルも同じだけ回転するという性質) を組み込む必要があります。
今回は Graphormer[8]の実装を参考に、回転同変なアテンション機構をもつモデルを構築しました。
アーキテクチャを以下に示します。
ポイントは出力層で相対座標との行列ベクトル積をとることで、座標が回転したときに、自動的に、出力も同じだけ回転するように設計している点です。
また原子間距離をアテンション機構の入力とすることで、他の対称操作に対する不変性も組み込まれています。
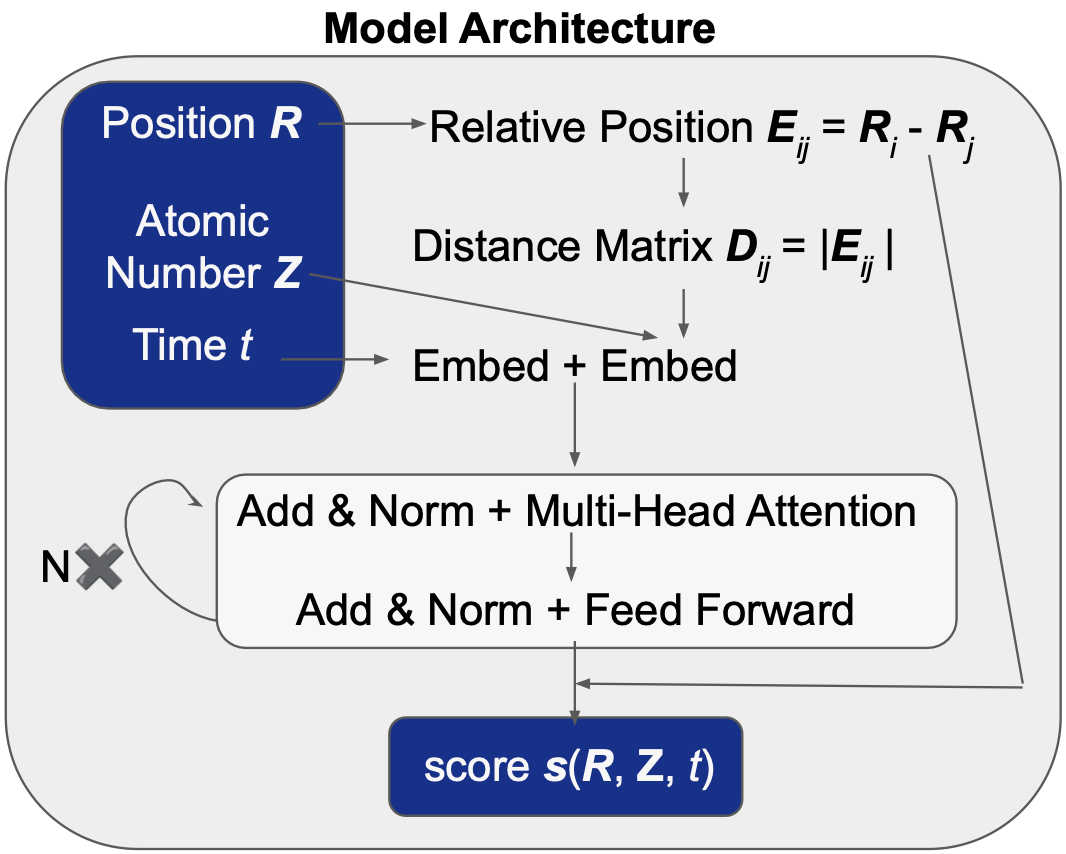
図5: Model Architecture
拡散モデルでは、機械学習ポテンシャルとは異なり、時間も引数にとっていることに注意が必要です。
時刻 \(t=0\) では分子の対称性を考慮する必要がありましたが、\(t>0\) においても同じ対称性を保持したまま拡散させる必要があります。
式 (1) のSDEに基づく拡散過程の場合、第一項は \(\mathbf{x}_t\) を平行移動すると、異なる値を返すため、このままでは平行移動に対する対称性がありません。終状態の正規分布が平行移動に対して対称性を持たないことからも明らかですね。
一方で、スコア関数 \(\mathbf{s}^\theta(\mathbf{x}, t)\) は分子力場が満たすべき性質から平行移動をしても常に同じ値を返すように設計しています。
これでは、モデルが拡散過程を正しく記述できません。そこで今回はノイズから平行移動の成分を除いて[9]、常に分子の重心が原点にあるような過程を考えてみました。
アーキテクチャと拡散過程の説明はここまでとして、以下では計算結果を示します。
以下の例では、教師データはすべてPFNが開発する機械学習ポテンシャルPFP[7]で用意しました。
まず、水分子に対して物理方程式学習を試してみました。
十分な数の構造点に対して学習後の \(t=0\) におけるスコアを以下に可視化してみました。
方向、スケールともに真の値を再現できているように見えます。
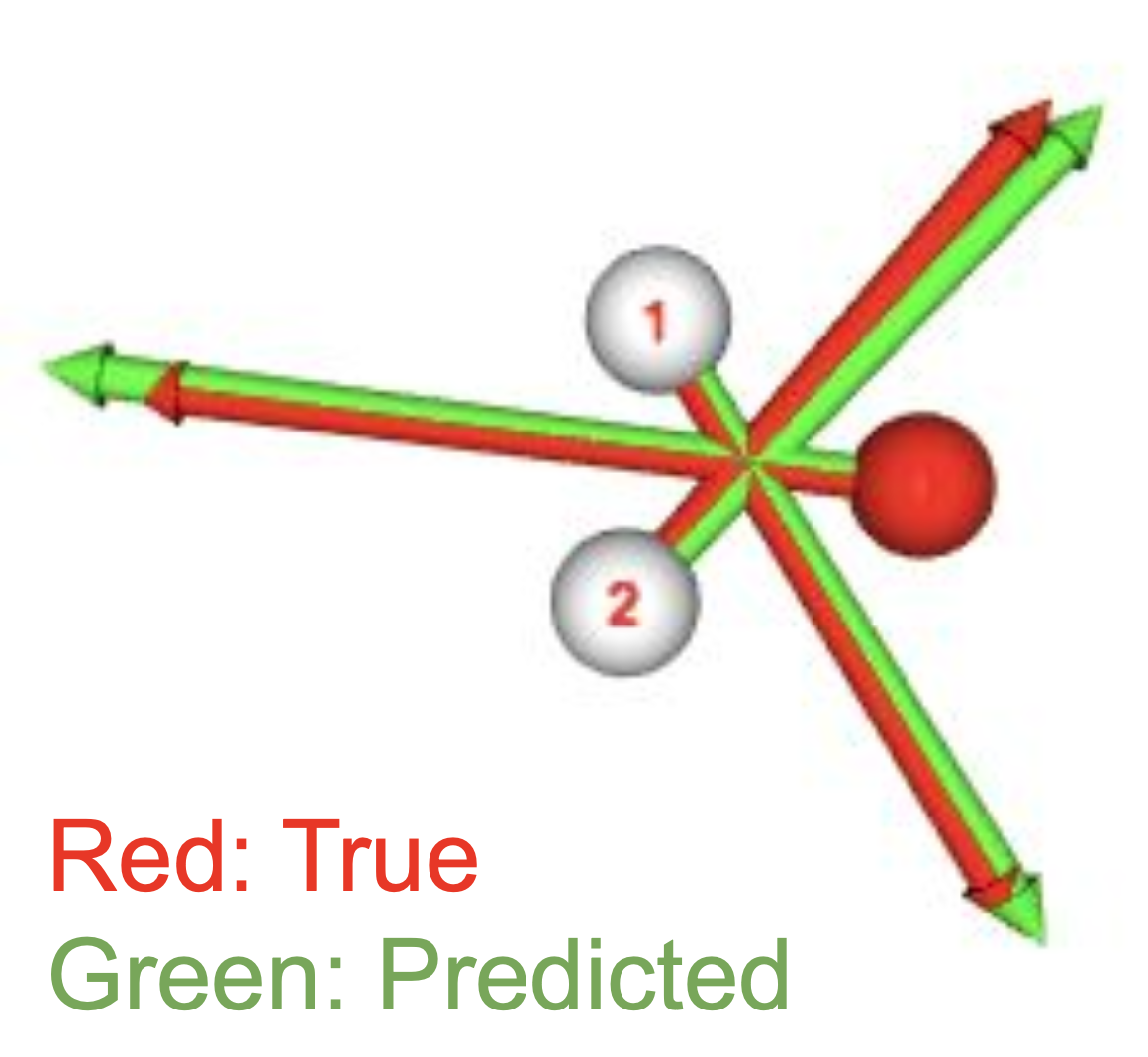
図6: \(t=0\) におけるスコア
一方で、損失関数 (4) の第一項は訓練が非常に難しく、スコアが満たすべきFokker–Planck方程式の左辺と右辺を可視化してみたところスケール、方向ともに全く合いませんでした。この理由については後ほど考察します。
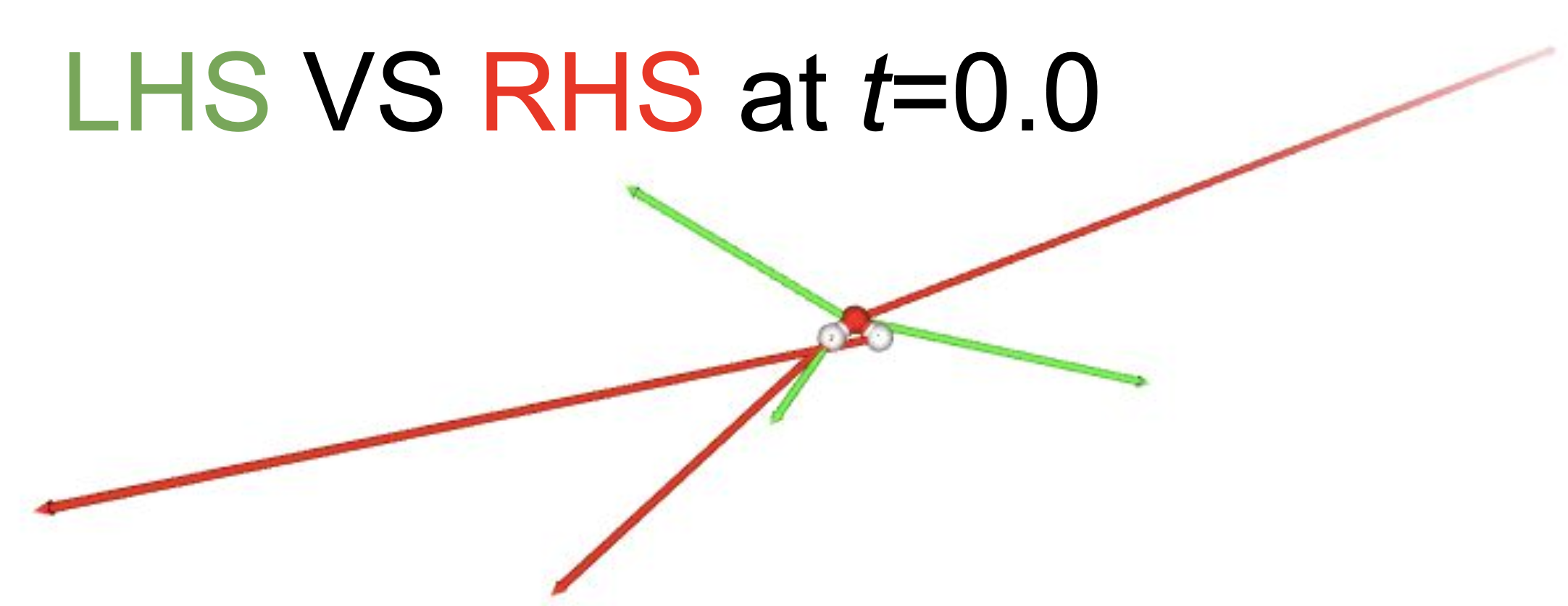
図7: スコアが満たすべきFokker–Planck方程式の左辺と右辺
図8: グリシンの構造式
次に、より難易度の高そうなグリシン分子 (10原子系) に対して、データ学習型の拡散モデルを試してみました。 (水分子でデータ学習型を試しても同じような結果が得られます。)
学習データは300KにおけるMDの軌跡としました。
実際、試してみると、分子サイズを大きくしたとしても、データ学習型の場合は容易に訓練が可能なことがわかりました。
訓練後のモデルで生成したグリシン分子を以下に示します。
ランダムに配置された原子が拡散モデルの逆過程によって、グリシン分子の構造に復元されていく様子がわかりますね。
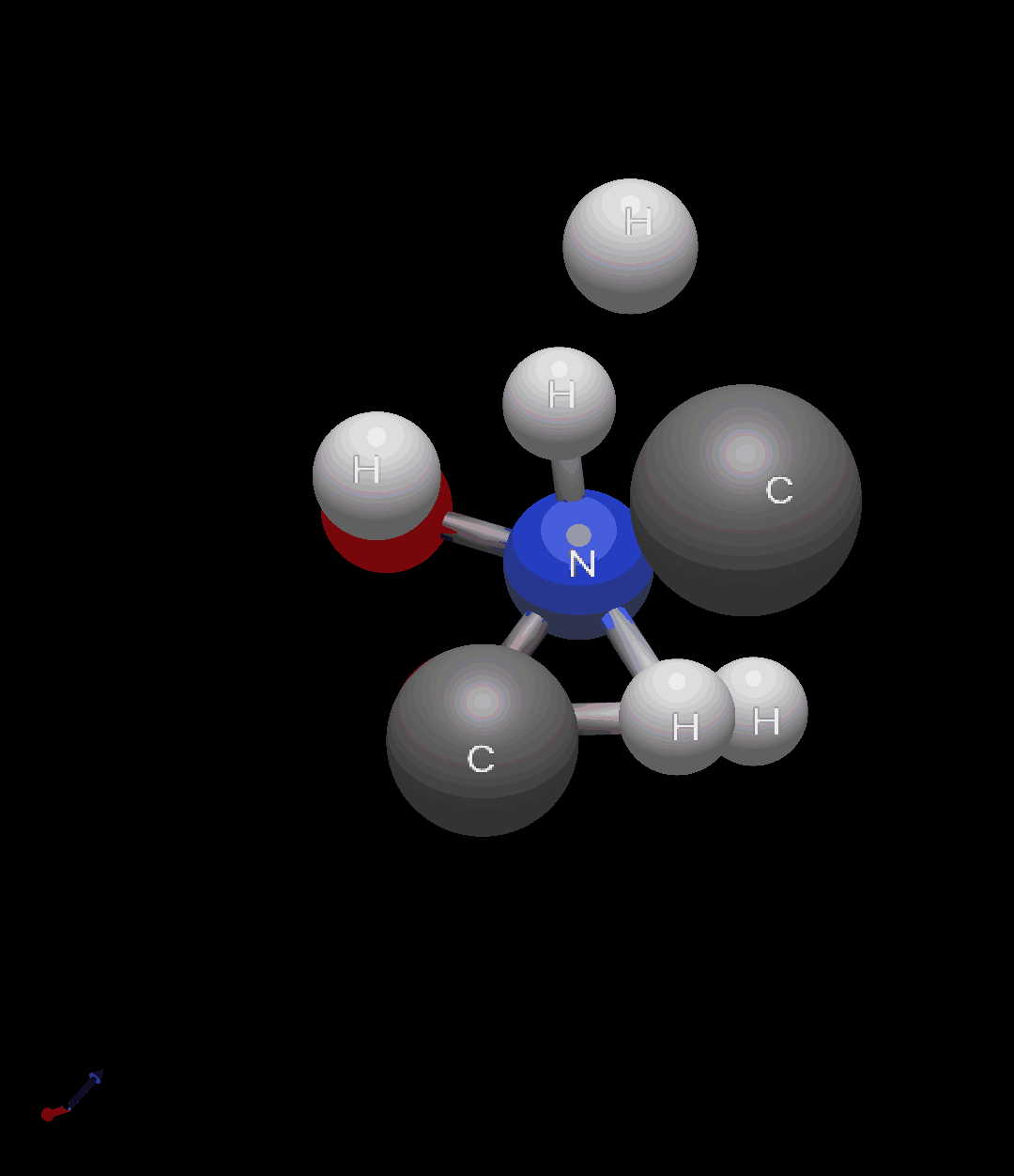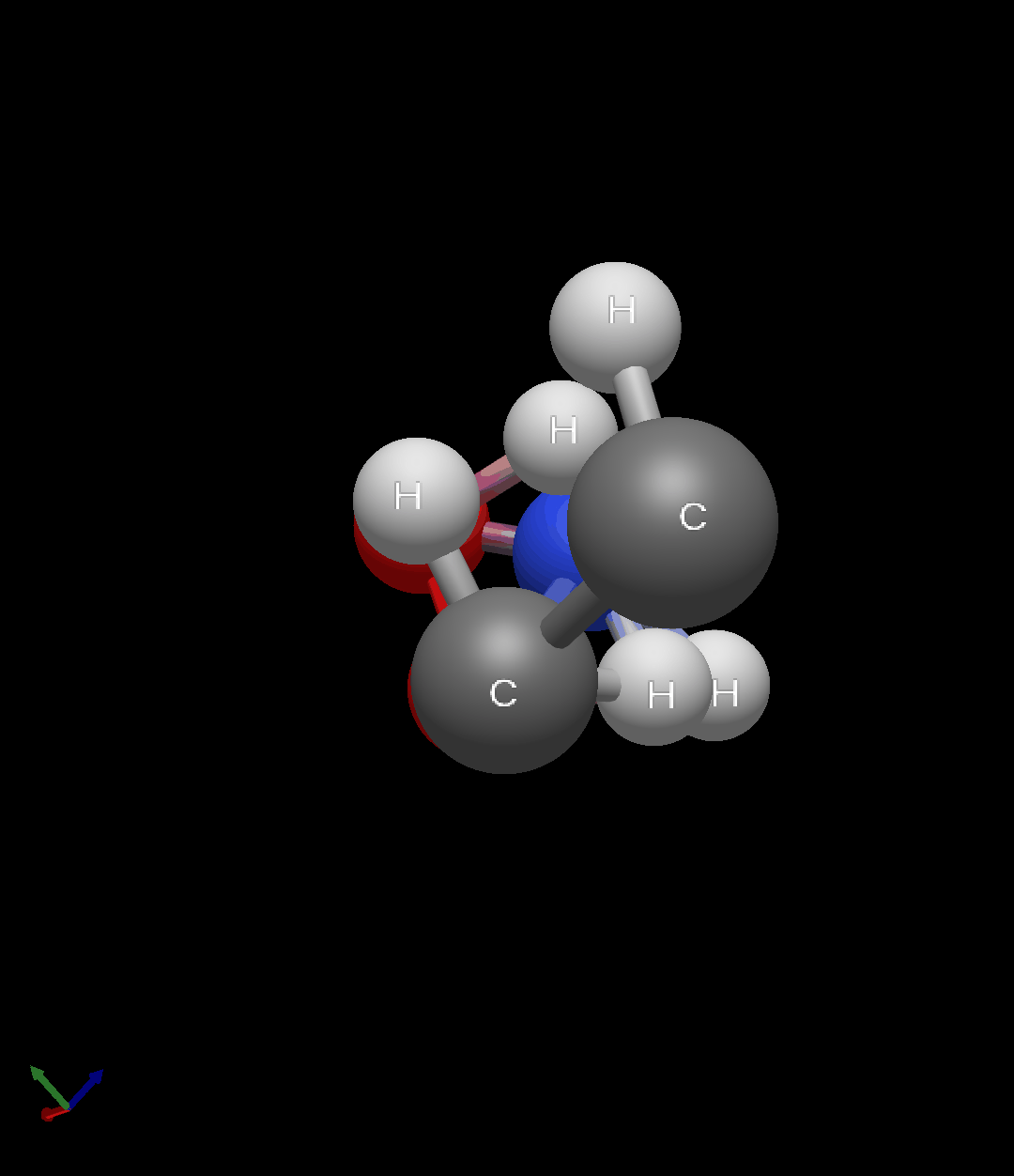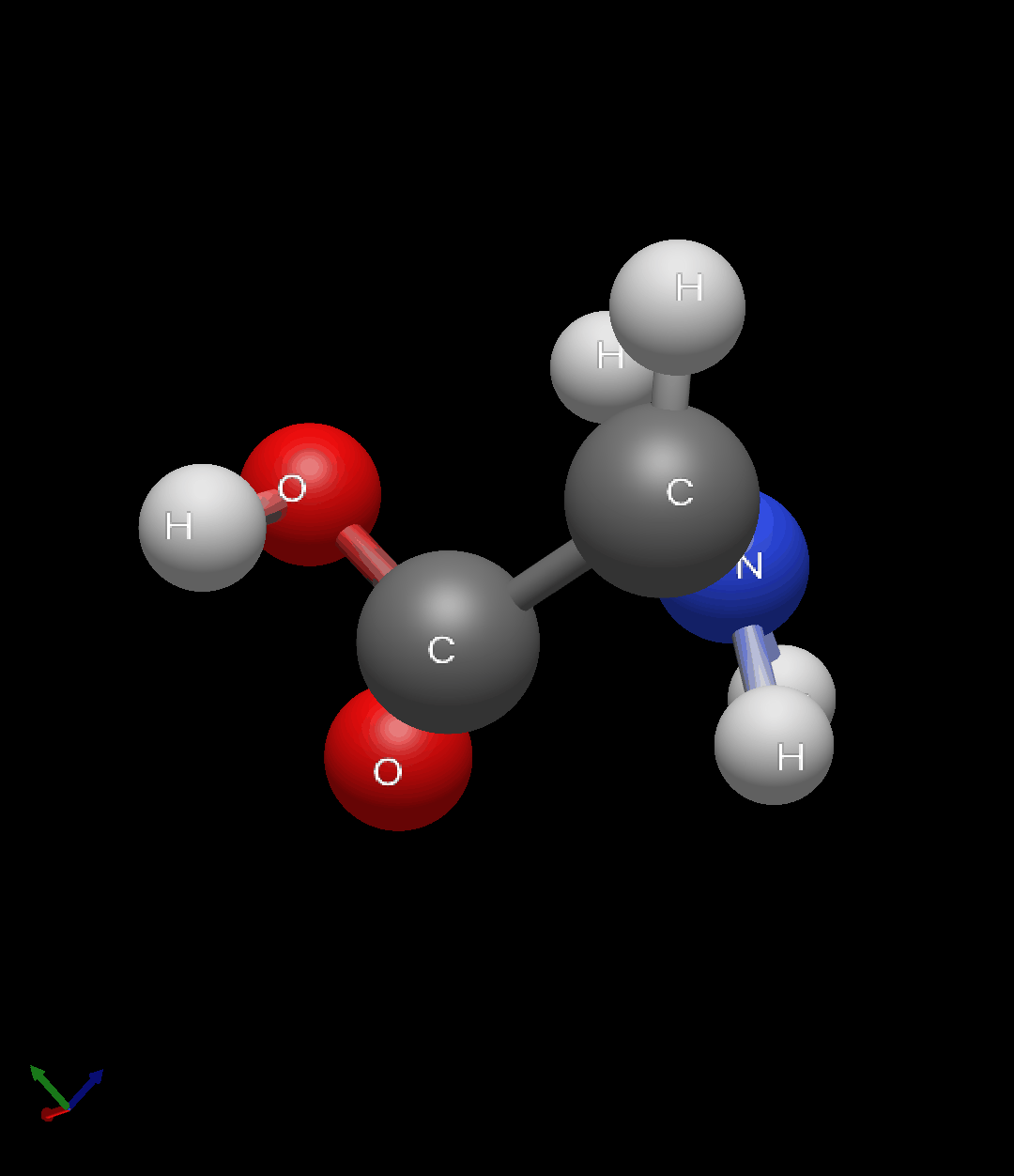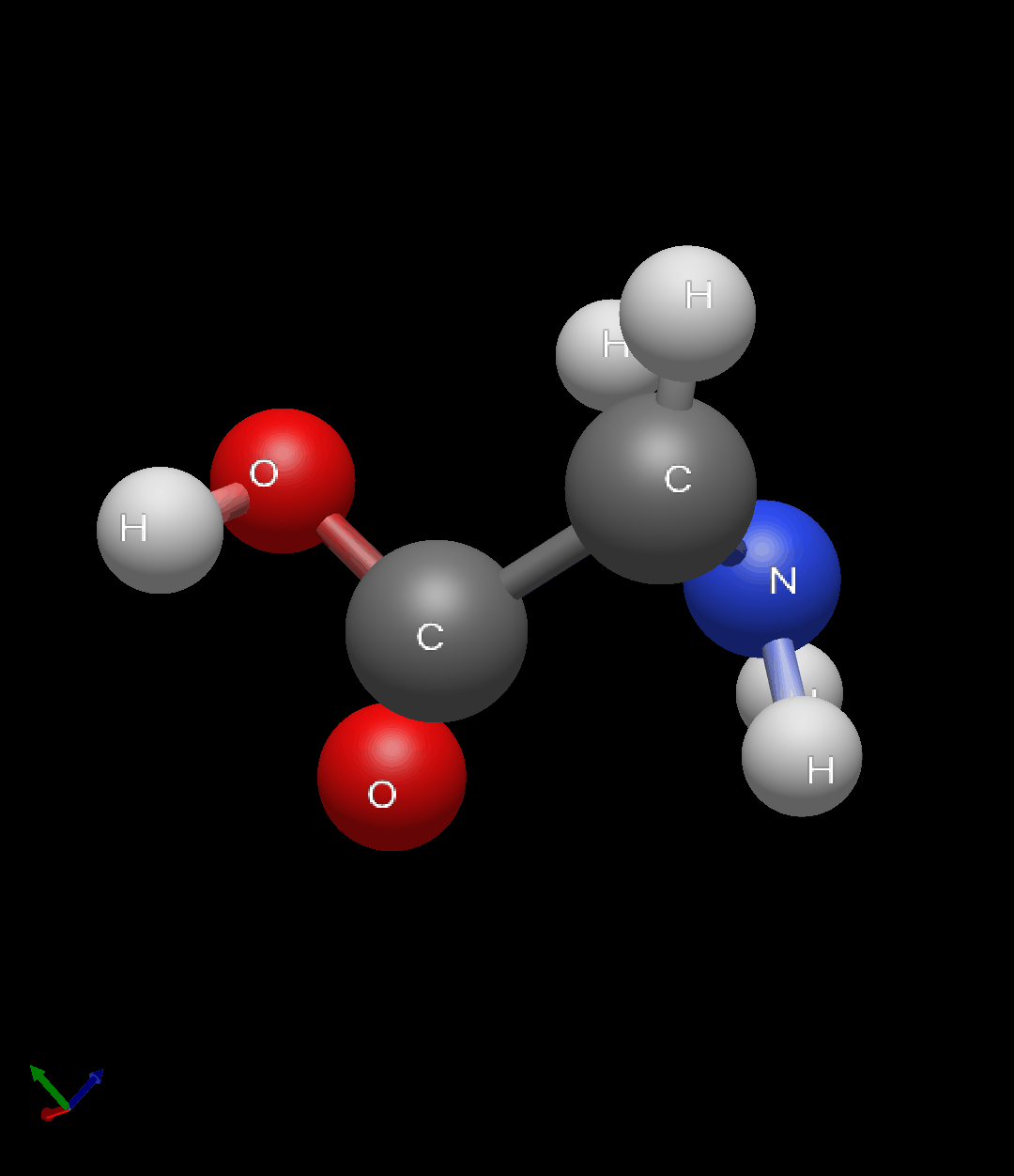
図9: グリシンの生成過程
こうして生成される構造の分布を定量的に評価しました。
以下に、(H-)O-C-Cを含む面と、C-C-N(-H2)を含む面のなす角の分布を以下に示します。
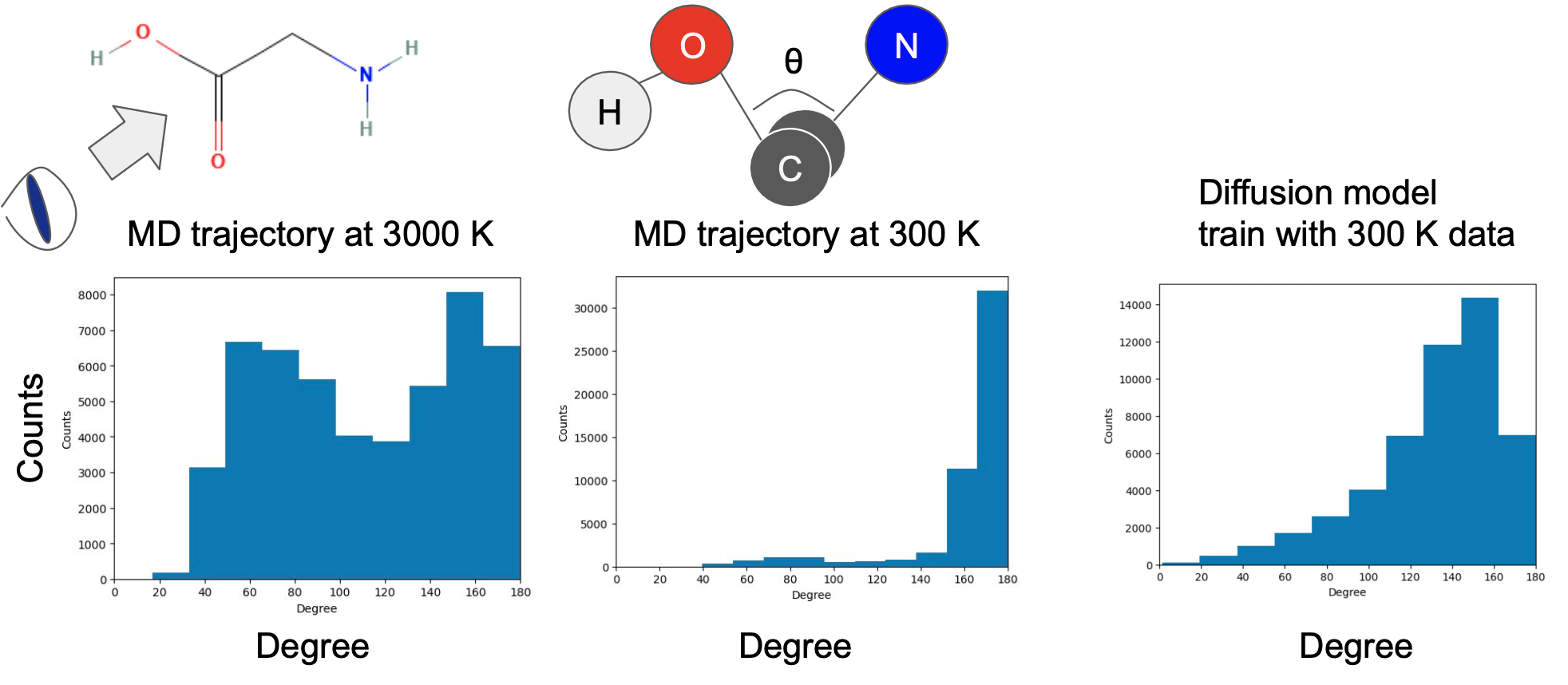
図10: 二面角の分布。左: 3000KにおけるMDの軌跡の構造、中: 300KにおけるMDの軌跡の構造、右: 300KのMDの軌跡を学習した拡散モデルで生成される構造
300KのMDの軌跡 (中央のヒストグラム) ではH-OとN-H2が反対側 ( \(\theta=180^\circ\) ) の位置にある安定構造が多数出現しますが、3000Kといった高温な環境のMDの軌跡 (左側のヒストグラム) では、エネルギー障壁を超えて同じ側にある構造も一定数出現することがわかります。
今回の拡散モデルは300Kのデータを元に学習しているため、理想的には300Kと同じような構造分布に基づいて生成されるはずですが、右側のヒストグラムのように、不安定でばらつきのある構造が生成されていることがうかがえます。
実際に、拡散モデルによって生成される構造に対して、エネルギーを計算すると、数十eVという、MDの軌跡に表れるエネルギーよりオーダーが1桁大きい物理的に意味をなさない値を返してしまうことが多々ありました。
これは、原子の運動自由度がとりうる高次元空間の大きさに対して、安定な分子として成立しうる空間の大きさは、私たちの想像よりはるかに小さいことを示唆しています。
以上をまとめると、データ学習型のモデルは訓練が容易で、人間の目では定性的に妥当な分子構造が生成されているようには見えますが、実際に生成される分子構造をそのまま使って定量的な物性計算を行うことは難しく、あくまでも多峰性のある分子構造の分布を網羅するための軌跡の初期値として用いる、といった用途の方が実用的ということが言えます。
再び2次元系 (Morseポテンシャル)
分子系において、データ学習型の訓練に比べて、物理方程式学習型の訓練の方がはるかに学習が難しいことがわかりました。
実際、先行研究[3]でも、物理方程式学習だけによって定量的な結果を得られることはできていません。
この難しさは分子系の自由度の多さに起因するものなのか、それとも、分子系のBoltzmann分布の形状が病的なために困難であるのかという疑問が生じます。
そこで、初めに学習がうまくいった、2次元のモデル系の分布関数をより分子に似たものに差し替えてみました。
ここで使う人工的な分布関数 \(\exp(-\beta E)\) は \(r=\sqrt{x^2+y^2}\) という原点からの距離によって特徴づけられており、エネルギー関数 \(E(r)\) は原点近傍で非常に大きな値を返し、\(r=2\) で最小値をとり、\(r\to\infty\) で0になるような関数です。
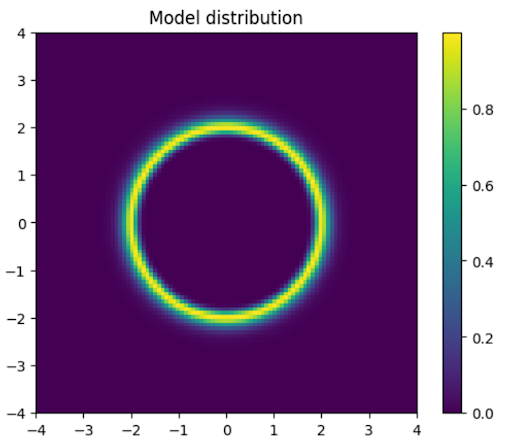
図11: 2次元モースポテンシャルのボルツマン分布
この分布関数を初期分布として、先ほどの2次元モデル系と同じ訓練を実行してみます。
得られたスコア関数は下の画像のようになり、スコアの方向が明らかにおかしい挙動を示していることがわかりますね。
(例えば、リングの内側のスコアが回転していたり、リングの外側のスコアはつねに中心を向いて欲しいですが、外側を向いてしまっていたりします。)
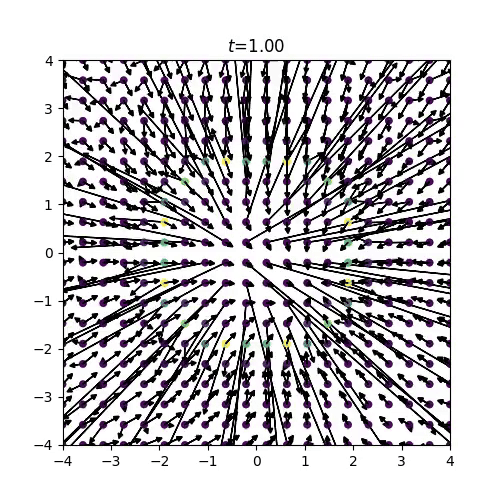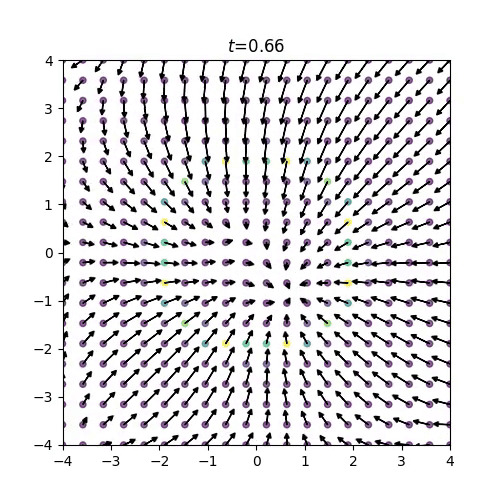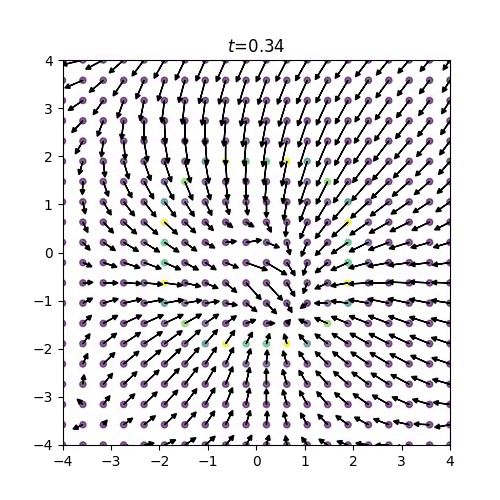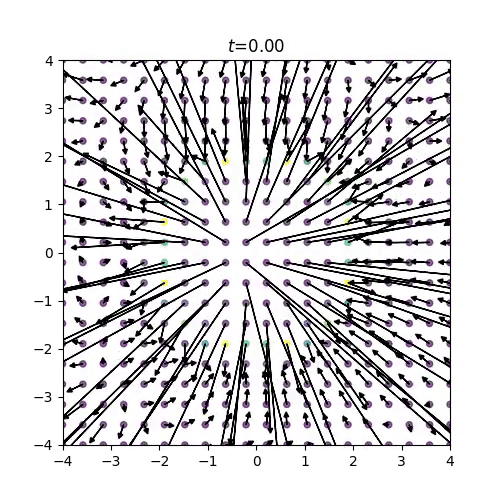
図12: 2次元モースポテンシャルの学習済みスコア関数
分子系の自由度の多さももちろん学習の難しさに影響を与えているはずですが、このトイモデルの結果から、そもそも始状態の分子のBoltzmann分布と終状態の正規分布をニューラルネットワークによって滑らかに接続させることが難しい、という仮説が立ちます。
そして、その理由は主として以下の3点に起因していると考えています。
1. 分子のBoltzmann分布のスコア関数は特異点を大量に含み、特に原点付近の振る舞いが正規分布と全く異なる。
2. Fokker–Planck方程式を学習するには、エネルギーの座標に対する2階微分以上の精度が求められる。
3. 物理方程式学習は、若い時刻から帰納的に学習を進める必要がある。
まず、1.について説明します。
正規分布で最も確率密度の高い点は原点 \(\mathbf{x}=0\) ですが、Boltzmann分布における原点は、すべての原子が衝突するような最も確率密度の低い点であり、その対数勾配は特異点になっています。
そのため、ニューラルネットワークで表現することが難しかったということです。
さらに、分子系は原子が離れすぎると、相互作用がなくなってしまい、スコアが \(\mathbf{0}\) になってしまいます。
そのため、正規分布の分散を極端に大きくするというアプローチも難しそうです。
この問題を解決するには、拡散変数として、分子のCartesian座標 \(\mathbf{x}\) を直接用いるのではなく、粗視化変数を用いる[2]、何らかの変数変換をする[10]、安定な参照構造からの変位を拡散変数として用いる[11]といった手段で、拡散過程において、特異点を踏みにくくするのが大事でしょう。
次に、2.について説明します。
物理方程式学習型の損失関数 (4) の第一項に、スコア関数の微分、すなわち、エネルギー関数の2階微分が出現しており、これが問題を難しくしています。
これは、スコアの発散 \(\nabla\cdot\mathbf{s}\) の計算コストが大きいという意味もありますが、それ以上に、そもそも2階微分が滑らかになっていないと、スコア関数が自己無撞着に偏微分方程式を満たすように学習するのが難しいということです。
水分子の例で計算したスコアの発散 \(\nabla\cdot\mathbf{s}^\theta\) のある方向の微小変位に対する振る舞いを可視化してみます。
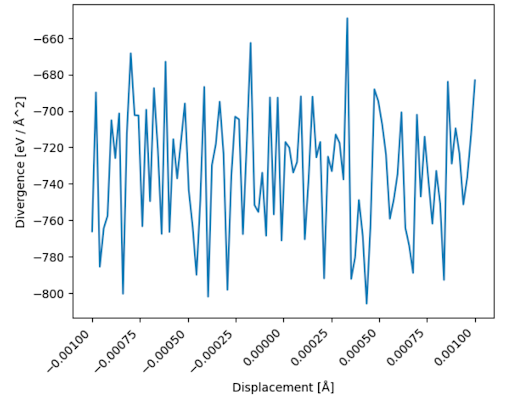
図13: 水分子のスコアの発散の振る舞い
このグラフからわかる通り、ニューラルネットワークが返すスコアの発散 (エネルギーの座標に対するHessian行列の対角和) の振る舞いが非常に不安定であり、Fokker–Planck方程式の右辺を、左辺 \(\partial\mathbf{s}/\partial t\) でフィッティングするのは無理がありそうです。
この問題の解決策としては、密で十分なサイズのバッチを使って倍精度の有限差分法で2階微分を評価したり、2階微分が妥当な値を返すような損失関数を加えるといった方法が思い浮かびます。
3.は物理方程式学習全般に言えることです。
入力変数の時空間のある点で真の解から外れる損失関数のスパイクが起こると、それより先では、自明な解 (trivial solution) に陥って意味のない学習をしてしまうことがあります。
たとえば、スコア関数のFokker–Planck方程式は自明な解 \(\mathbf{s}=0\) を持ちます。
ですので、ある時刻でスコアがつねに \(\mathbf{0}\) を返すような状態に陥ってしまうと、見かけ上、損失関数は下がっているが、それは意味のない学習をしている、といった状況があり得ます。
この現象は容易に発生して、以下のように、時刻 \(t\in[0, 0.10]\) のみで訓練した場合でも \(t=0.02\) 以降では自明な解に陥ってしまいました。これは、各離散化時刻ステップを独立に学習できる、データ学習型のモデルでは起きない現象です。
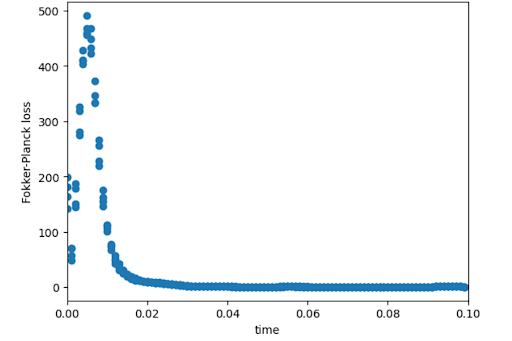
図14: Fokker–Planck方程式の損失関数にスパイクがおきる様子
この問題を解決するには、学習時間の区間を非常に小さくとる必要があります。
また、スパイクが起きる点で損失関数の入力に対する勾配が急激に変化していることから、「損失関数の入力 (上のグラフでいう横軸の時間 \(t\)) に対する勾配のノルム」を損失として加えるといったアプローチ[12]も考えられます。
さらに、 \(\partial \mathbf{s} / \partial t\) を離散化することで
\(\mathbf{s}^{\theta}_{i+1}(\mathbf{x}) =\mathbf{s}^{\theta}_{i}(\mathbf{x})+ \frac{\beta_{i}}{2}\nabla\left[\left(\mathbf{x}+\mathbf{s}^{\theta}_i(\mathbf{x})+\nabla\right)\cdot \mathbf{s}^{\theta}_i(\mathbf{x})\right]\)
から各離散化時刻 \(i\) ごとに、ニューラルネットワークを組んで帰納的にモデルを学習するというBrute-force的なアプローチによって、後の時刻で自明解に陥ってしまっても、その結果に引っ張られにくくするといった策も思い浮かびます。
まとめ
拡散モデルによって定量的な分布を再現することを目標に、一般的なデータ学習型の訓練と、物理方程式学習型の訓練を試してみました。
どちらの方法も、それぞれの良し悪しがありましたが、現状の拡散モデルでは、データ学習型の方が定性的な要求を満たすためであれば、うまい結果が得られやすいということが分かりました。
一方で、物理方程式型学習の方法を確立し、汎化することができれば、物性予測など定量性が求められる分野での大きなブレイクスルーになることが期待できますが、その道はもう少し長そうです。
また、PFPのように高階微分の精度で正しい振る舞いを示すモデルをFokker–Planck方程式に従って若い時刻から帰納的に数百から数千ステップ分構築することで定量的な拡散モデルは原理的に作れる可能性も感じました。
いずれにせよ、生成モデルを使った定量的な材料探索には、高精度な機械学習ポテンシャルのノウハウが必要不可欠である、ということを最後に述べておきます。
謝辞
本テーマは私が興味はあったものの一人では手が出せなかった領域を詰め込んだようなものでしたが、1ヶ月半という短い期間で、確率過程の基礎の習得、PFPを使ったMD計算、拡散モデルの課題までキャッチアップすることができ、非常に満足しております。
本課題の遂行にあたって、成果物を残してくださった昨年度インターンの坂部さん、環境整備や議論に加わっていただいたPFNの社員の皆様、特にメンターを務めてくださった林さん、森さんに感謝申し上げます。
引用
[1] 岡野原大輔 拡散モデル: データ生成技術の数理; 岩波書店, 2023.
[4] https://tech.preferred.jp/ja/blog/free-energy-estimation-using-diffusion-model




