Blog
海野です。
先日会社の論文読み会で、ICML2014のMaking the Most of Bag of Words: Sentence Regularization with Alternating Direction Method of Multipliersという論文を紹介しました。さて、この時話題になったのが正則化項をグループ化すると何でグループごと重みが0に潰れるのかという話でした。式を見ても直感的にはわからなかったのですが、得居さんがとてもわかり易い説明をしてくれました。この話、日本語で検索してもあまり出てこないのでちょっと紹介します。
まず、Lassoというのは、正則化項にL1normを使ったいわゆるL1正則化のことで、大部分の重みが0に潰れて疎な解が得られます。
\(\Omega_{\mathrm{lasso}}(\mathbf{w}) = \|\mathbf{w}\|_1 = \sum_i |w_i|\)
この進化形として、Group Lassoという手法があります。Group Lassoでは、重みベクトルの次元をグループ分けして、各グループごとのL2norm(L1じゃないよ)の総和を正則化項として使います。具体的な式は以下のとおりです。
\(\Omega_{\mathrm{glas}}(\mathbf{w}) = \sum_g \|\mathbf{w}_g\|_2\)
ここで、gは特徴次元をグループ分けした時の、各グループを示します。Group Lassoを使うと、重みが潰れるときはグループ内の重みがいっぺんに潰れやすくなります。こうすることで、事前に類似の傾向がありそうな特徴の情報をいれこむことができます。ところで何でいっぺんに潰れるのでしょう。式を見ても直感的にわかりません。等高線を使った図で説明します。
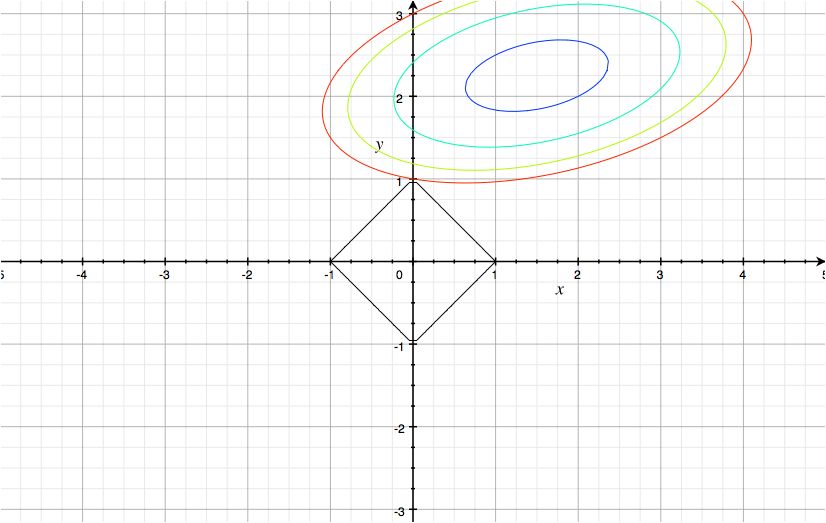
その前に、LassoつまりL1正則化で重みが0に潰れやすい理由の復習です。入力次元が2次元として等高線を使った説明をします。入力が2次元の時、正則化項が同じ値になる領域(等高線)は原点を中心とする菱形になります(下図の黒線)。さて、一方の損失関数は何かしらの凸な関数ですので、等高線は丸っぽい形になります(下図の色線)。幅は外に行くにつれて狭まっていきます。この2つの和が最小の点を探すわけです。
ここで、最適点の時の正則化項の値が仮にわかっていたとして、それが図の菱型上のどこかだとします(もちろんこういう風に最適化するわけではないですが)。この時、最適点はどこでしょう? ここで、損失関数の等高線を見てみます。損失関数の値もなるべく小さいほうがいいので、菱型と交わる等高線の内、最も内側の等高線が最適です。内側の等高線から外側に見ていって、一番最初に菱型と接する等高線を探せば良いわけです。
ではどんな点で接しやすいのでしょうか。ここで大事なのは、正則化項は菱型をしている、つまり尖っているのです。丸い損失関数の等高線を大きくしていくと、正則化項の尖っている点と接しやすいのはイメージでわかりますね。そして、尖っている点はどんなところかというと、いずれかの次元が0になっている点です。そのため重みが0に潰れやすくなります。大事なのは尖っている点が最適点になりやすいという性質です。
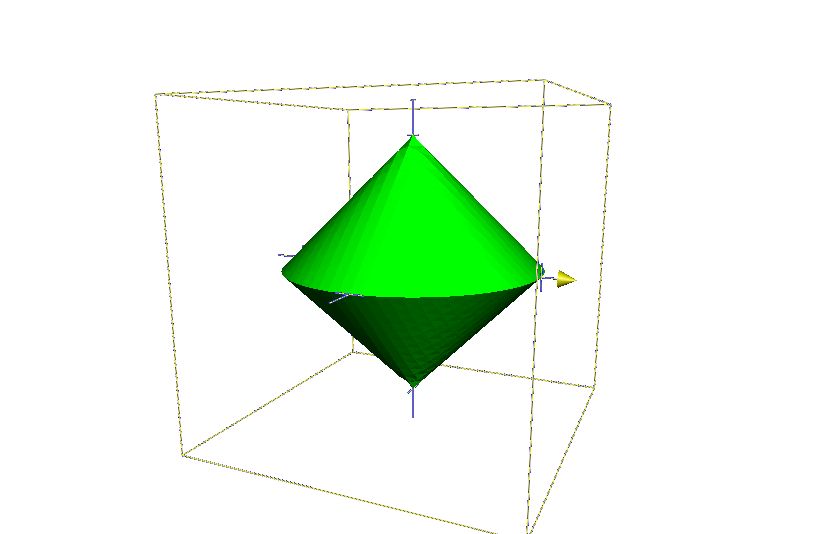
長くなりましたが、ここまでが前置きです。ではGroup Lassoの正則化項の等高線はどうなっているでしょう。下の図は、\(\sqrt{x^2 + y^2} + \sqrt{z^2}=C\)の図です。入力は3次元です。
xとyが同一グループになっています。この時、3次元空間中で等高線(面?)は円錐を2つたしたような形になっています。先の菱型ではなくて、円推になるのはz=0の平面上で、\(\sqrt{x^2 + y^2}=C\)の円ができるというイメージです。ここが単なるLassoの場合は、円ではなくてやはり菱形になることに注意して下さい。
では、どんな点で最適点になりやすいか。もうわかったと思いますが、尖っている部分です。つまり、円錐の先と、円錐の縁の部分です。これはそれぞれ、前者がx=y=0の、後者がz=0に対応しており、各グループの値が全部0になっていることと対応しています。1つのグループ以外が全部0になっているとすると、正則化項は残りの次元で形成される球の式になります。これが円錐の縁に対応しているわけです。このとき、同一グループ内ではなめらかなため、グループ内のどれか一つだけが0になるということは起きにくいのです。さきの図の場合、z=0の平面中で円(xとyの2次元なので)になっているため、xかyだけが0になるということは起こりづらく、0になる時はみんな一緒に0になるわけです。
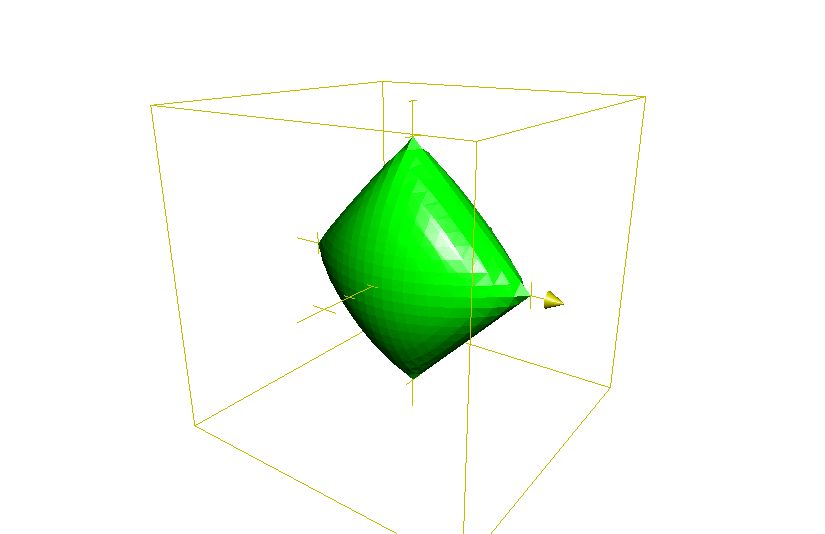
さらに、論文にあるようなグループに重複があるときはどうなるでしょう。下の図は\(\sqrt{x^2+y^2} + \sqrt{y^2+z^2} = C\)のグラフです。このとき、座布団のような形をしています。このとき尖っているのは、第1グループが全部0のx=y=0のときと、第2グループが全部0のy=z=0のときです。
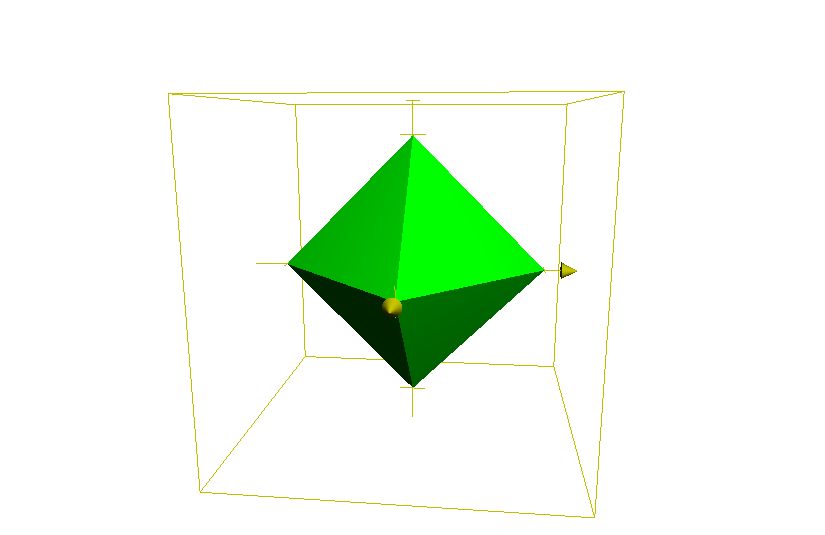
ちなみに、同様に入力が3次元のとき、Lassoは多次元菱型(?)になります。これは先の円錐2つに比べるとより尖っていて、そのため各頂点に最適解がみつかりやすいという風に振る舞うわけですね。各頂点は1つの次元以外は全部0というわけですから、独立にそれぞれの重みベクトルの値が0になりやすいということです。
最後に、このグラフ簡単にプロットできないかなぁと思ったらMacにはGrapherというツールがデフォルトでついていました。方程式を入れたらあっさりプロットしてくれました。Macスゴイ。
Tag