Blog
はじめに
こんにちは!Material &Drug discovery チームの森です。普段はリサーチャーとして研究開発に従事する傍ら、エンジニアリングマネージャーも兼任しています。PFNに加わる前は素材メーカー、自動車部品メーカーで高分子の材料開発や計算化学、マテリアルズインフォマティクスに関する業務に携わっていました。実験と計算のキャリアはちょうど半分ぐらいで、ようやく最近計算のキャリアの方が長くなってきました。PFNには機械学習だけでなく、私のようにいわゆる実験系出身の人も働いています。
この記事では弊社深層学習用プロセッサーのMN-Core 2を活用して自由エネルギーを効率的に計算する試みについて書いています。
自由エネルギーとそのシミュレーション
化学現象を理解するうえで最も重要な熱力学量に自由エネルギーがあります。自由エネルギーは物質の安定性や状態の出現頻度を示す指標として機能し、化学反応における反応物と生成物の比例関係や反応頻度といった情報の把握に非常に重要です。エネルギーと混同されがちな自由エネルギーですが、自由エネルギーにはエントロピーの要素が組み込まれている点が異なります。
しかし、自由エネルギーが物理量として重要である一方、自由エネルギーをシミュレーションで求めることは難易度の高い課題として知られています。これは前述のエントロピーが原因となっています。エントロピーは状態数に対応するため、特定の状態の自由エネルギーを計算するためには、その状態のすべての数を計算する必要があります。これはほとんどの場合、非現実的な計算量になります。自由エネルギーの絶対値を計算することは依然として困難な問題ですが、一方で、実用的には自由エネルギーの絶対値ではなく、その相対的な変化に関心があることがほとんどです。ある状態と別の状態における相対的な自由エネルギー差は、自由エネルギー摂動法や熱力学積分法 [1-3]、メタダイナミクス [4]などによって可能となっており、材料開発や創薬など広い分野で利用されています。実際に弊社でもP-FEPという名称でRelative Binding free energy perturbation (RBFEP)の受託サービスを開始しています。
自由エネルギーのシミュレーションの課題
次に、具体的な自由エネルギー計算方法とその課題について解説します。化学反応を例に挙げて、A+B → ABという付加反応の自由エネルギー曲面(Free energy surface, FES)を求めることを考えてみます。まず、自由エネルギーを計算するにあたって、シミュレーションモデル上での反応を特徴づける変数を決める必要があります。この変数のことを集団変数 (Collective variables, CV)といいます。集団変数は原子間の距離や角度やこれらを組み合わせた関数、配位数など様々な量を利用できます。また最近では機械学習を用いた集団変数も提案されています [5]。今回取り上げる付加反応は、A, B分子間に結合が形成される反応であり、このケースでは集団変数として特定の原子間距離が考えられるでしょう。ある集団変数sに対する自由エネルギー\(F(s)\)は統計力学に基づいて次のように表すことができます。
$$F(s) = – k_bT\log(p(s)) \tag{1}$$
ここで\(k_b\)はボルツマン定数、\(T\)は絶対温度を表します。式 (1)に基づいて、ある集団変数\(s\)の確率密度\(p(s)\)を求めるというのが基本的な発想になります。\(p(s)\)の求め方として分子動力学 (Molecular dynamics, MD)シミュレーションによって\(s\)をサンプリングするという方法が考えられます。しかし、シンプルなMDのみで自由エネルギー変化を求めることはほとんどの場合困難です。これは式 (1)の裏返しで、エネルギー的に不安定な状態の出現頻度は指数的に低くなるためです。これにより単純にMDを行っても安定構造のみがサンプリングされ、遷移状態の近傍はほとんどサンプルされないという問題が起こります。
この問題に対処するための方法は様々開発されていますが、代表的なものにエネルギー的に安定で出現確率が高い状態に対してバイアスポテンシャルを付与するという方法があります。こうすることで系が全体的に不安定になり、様々な状態を効率的にサンプリングすることができます。これらの方法はアンブレラサンプリングやメタダイナミクスとして良く知られています [4, 6]。バイアスポテンシャルの存在下で獲得された確率密度は、本来の確率密度とは異なりますが、確率の再重み付けにより元の確率密度に戻すことができます。また、バイアスポテンシャルの与え方を工夫することで、よりサンプリング効率を高めるという研究も数多くなされています。最近開発された手法にOn-the-fly enhanced sampling (OPES) があります [7]。OPESは、MD中にサンプリングされた確率密度に基づいてバイアスポテンシャルを決定するというものでメタダイナミクスよりFESが高速に収束することが報告されています [7] 。
しかし、これらの工夫を行ったとしても、依然として自由エネルギーを計算するには大量のサンプリングが必要であることには変わりません。例えば、古典MDを用いた自由エネルギー計算の代表的なベンチマークとして、アラニンジペプチドの異性化があります。これは二つの二面角の回転の自由エネルギー曲面を評価するものですが、これには数十ナノ秒のサンプリングが一般的に行われます [7, 8]。これは\(10^7\)オーダーのステップの計算に対応します。また、化学反応が重要になるケースでは第一原理計算などの反応が扱えるポテンシャルを用いる必要があり、実際に分子内ケテン-オレフィン環化反応 [9] やフルオロアルコール中のフリーデルクラフツアルキル化 [10]などの適用例があります。しかし、第一原理計算は計算コストが高いため、大量のサンプリングを必要とする自由エネルギー計算を化学反応に適用するのは依然として容易なことではありません。
PFP
反応が重要になる現象に対して迅速に自由エネルギー計算を行いたい場合、機械学習ポテンシャルが有効な選択肢となります。弊社とENEOS株式会社で開発しているMatlantisで用いているPFPは反応を扱うことができる機械学習ポテンシャルであり、DFT並の精度でありながらDFTよりも10,000倍高速に計算が可能です。さらに、PFPは任意の化合物に適用可能な汎用性を特徴としており、研究対象の物質ごとにfinetuneすることなく動作することが期待されます。PFPを用いることで従来は難しかった化学反応が関与する系の自由エネルギー曲面を現実的な時間で計算できると期待されます。実際にMatlantisでWell-tempered metadynamicsによって自由エネルギー曲面を解析するためのチュートリアル [11]がmatlantis-contribで提供されています。
MN-Coreを用いた自由エネルギー計算の高速化
しかし、PFPをもってしても多数の反応を計算したい場合にはさらなる高速化が望まれます。さて、高速化という観点では、計算コストの小さいポテンシャルの利用やサンプリング方法の工夫以外にも、高速な演算装置を使うというアプローチも考えられます。弊社ではMN-Coreシリーズという深層学習用プロセッサーの開発をしており、実際にMatlantis上でも一部のワークロードが提供されています。このMN-Coreを自由エネルギー計算に適用できれば、より短い時間でシミュレーション結果を得ることが可能となります。これにより計算結果を研究に高頻度にフィードバックを行うことができるため、より効果的な研究開発ができると期待されます。そこで今回は、化学反応の自由エネルギー計算にMN-Coreを用いることでどれだけシミュレーションが高速化されるのかを検証してみました。
検証
検証用のモデルにはメタクリル酸メチル (MMA)の3量体ラジカルとMMAの付加反応を用いました。この反応は成長反応と呼ばれ、アクリル樹脂を合成する際の中心的な反応の1つです。成長末端のラジカル炭素と\(\beta\)炭素の距離\(d\)を集団変数としています(図1)。
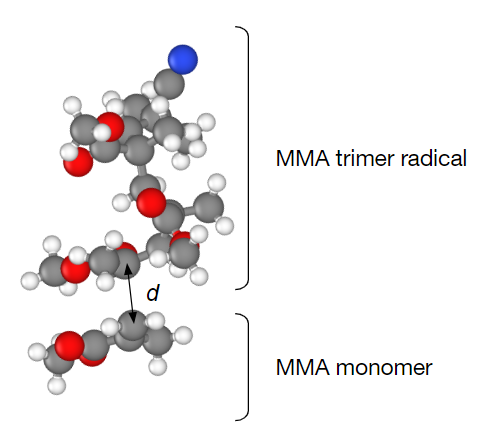
図1 検証に用いたモデル
シミュレーションは以下の条件で行いました。
- アンサンブル:NVT (\(T = 333\,\mathrm{K}\), 時間刻み \(\Delta t = 1\,\mathrm{fs}\))
- 熱浴:Langevin integrator (friction coefficient \(= 100\,\mathrm{fs}^{-1}\))
- サンプリング:OPES(barrier 2 eV, 100ステップごとにバイアスを追加)
- ポテンシャル:PFP ver.5.0.0 CRYSTAL_U0_PLUS_D3
シミュレーションにはOpenMM ver.8.1.1を用い、これらと合わせてPLUMED ver.2.8.2及び、及び自社開発したPFPのOpenMMインターフェイスを用いました。計算資源にはNVIDIA V100-16GB、MN-Core 2のいずれかを用いました。
シミュレーション結果を図2に示しました。\(d \approx\)1.5 Åが反応後、\(d > \) 4が反応前に対応します。図中の帯はブロック数 5のブロック解析によって得られたFESの95%信頼区間を表しています。ブロック解析については[11]でも詳しく説明しています。若干の差異はあるものの、MN-Core 2とGPUとの差は1 kcal/mol以内であることがわかります。1 kcal/molというのはいわゆる化学精度と呼ばれるもので、演算装置によってその精度が大きく損なわれているわけではないことがわかります。
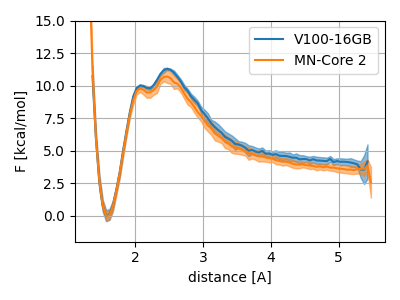
図2 GPUとMN-Coreの自由エネルギー曲面(FES)の比較
図2の計算が得られるまでの時間を示しました。MN-Core 2を用いた場合はGPUの6~7倍速く計算できており、より短い時間で結果が得られることがわかります。高速化の度合いは原子数やシミュレーションの内容に依存しますが、今回の問題ではサンプリングが律速であったためMN-Core 2による高速化の恩恵が大きく得られたと考えられます。計算時間をより実用的な観点でみると、今回のケースでは図2のFESを得るまでに8-9時間程度で済んでいるため、例えば会社から帰宅する前に計算を投入しておき、翌朝結果を確認するという使い方も可能かと思います。また、FESの推定誤差は一般的にサンプル数\(n\)に対して\(\frac{1}{\sqrt{n}}\)に比例するため、例えば同一の計算時間でよりFESの誤差を低減させるという使い方も考えられます。深層学習専用チップは速度や価格面に注目が集まることも多いですが、その速度を活かして、より高精度でリアルな結果を現実的な時間で取得する使い方も考えられます。
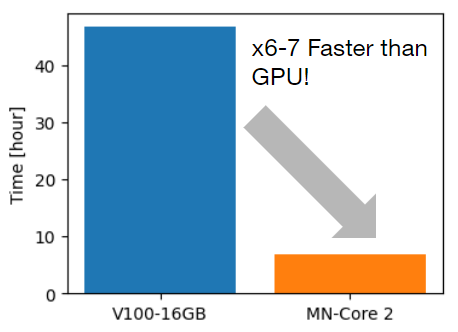
図3 図2のFESを得るまでに要した時間 (70原子, MD 2×10^6 ステップ。速度の向上効果は原子数によって変わります。)
応用例
先の例では真空中での反応を扱いましたが、溶液中での反応解析への適用も考えられます。アゾビスイソブチロニトリル (AIBN)はラジカル重合の開始剤で用いられる化合物で、熱によってメタクリロニトリルラジカル2分子と窒素に分解します。この分解反応のアセトン溶液中におけるFESを計算してみました。反応座標はアゾ基に隣接する炭素のそれぞれの距離(\(d_1\), \(d_2\))を採用しています。モデルはAIBN 1分子、アセトン 50分子としており合計で523原子となります (図5)。計算にはMN-Core 2を用いました。
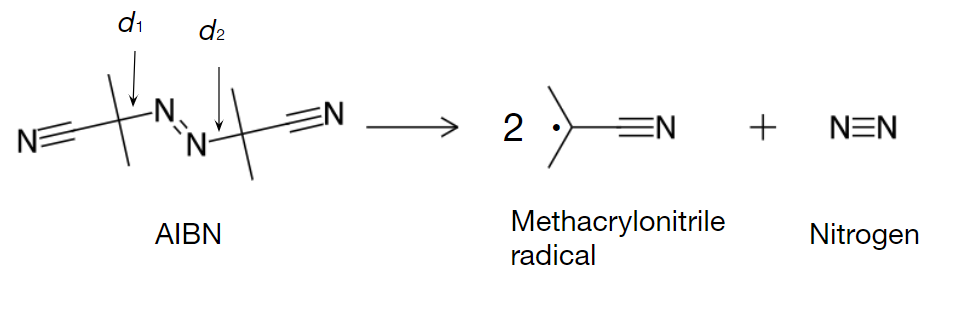
図4 AIBNの分解反応
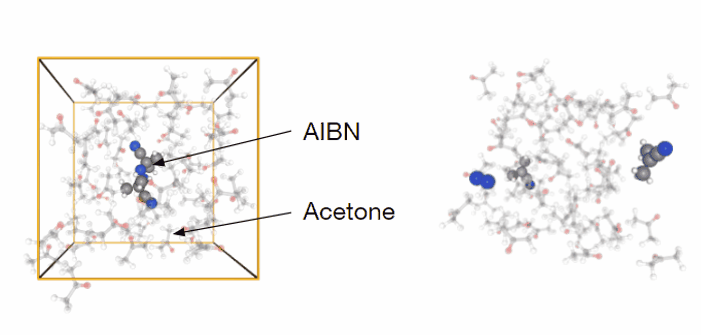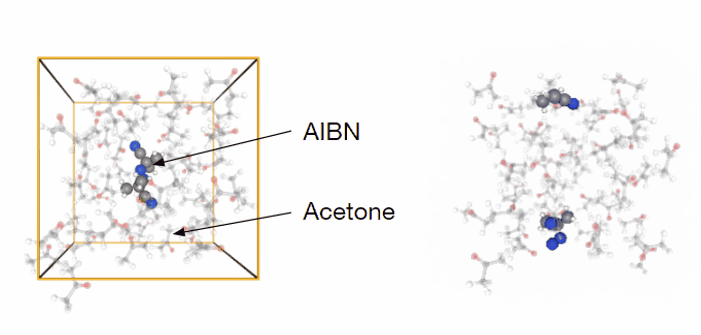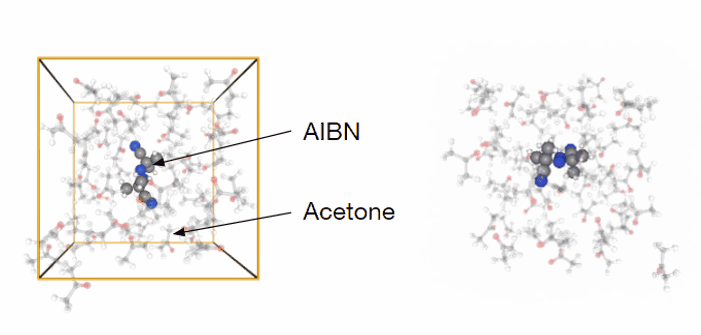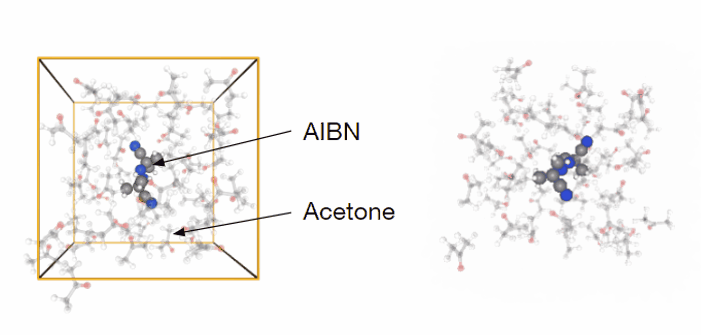
図5 シミュレーションモデル(アセトン溶媒中におけるAIBN。右図は実際のシミュレーションのトラジェクトリーを表しています。シミュレーションボックスは非表示になっています)
図6にAIBNの分解反応のFESを示しました。図6は約45時間でFESが得られています。\(d_1\), \(d_2\)の距離が大きい領域の自由エネルギーが低く、発熱反応であることがわかります。
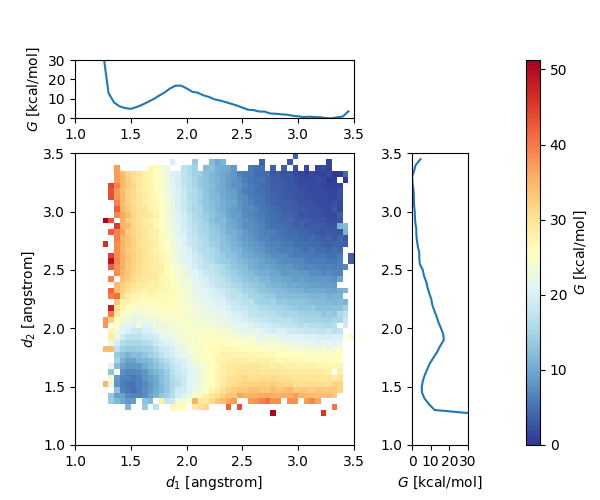
図6 AIBNの熱分解の自由エネルギー曲面 (523原子, 原子数MD 1.5 ×10^6 ステップ)
おわりに
本記事ではMN-Coreのアプリケーションとして高速な自由エネルギー計算を紹介しました。化学反応が関与する系の自由エネルギー計算はまだまだ少ないですが、機械学習ポテンシャルとMN-Coreを用いることで日常の研究開発に利用可能な段階に来ていると感じます。今回紹介したシミュレーションはいずれもプラスチックの製造やリサイクルに関係するものです。現代社会ではより高機能かつ環境にやさしいプラスチックの開発が急務であり、シミュレーションを含めて活発な材料開発が行われています。
Material &Drug dicoveryは、Matlantis以外にも材料開発を加速させる様々な技術の研究を行っています。一緒に研究開発を行うリサーチャー・エンジニアを募集しています。本記事を通して、ご興味を持っていただけたという方はぜひ下記ページをご確認ください。本記事のような原子シミュレーションの手法に関する知識を持っている方も歓迎です!
- Material Discovery Researcher / リサーチャー(材料)
- Matlantis Core Development Engineer / Matlantis コア技術開発エンジニア
- Matlantis Software Engineer in Test
参考文献
[1] J. P. Hansen and I. R. McDonald, Theory of Simple Liquids, 2nd ed., Academic Press, London(1986).
[2] M. P. Allen and D. J. Tildesley, Computer Simulation of Liquids, Oxford University Press, Oxford (1987).
[3] D. Frenkel and B. Smit, Understanding Molecular Simulation, From Algorithms to Applications, 2nd ed., Academic Press, London (2002).
[4] A. Laio, and M. Parrinello, “Escaping free-energy minima,” Proc. Natl. Acad. Sci. U. S. A. 99(20), 12562–12566 (2002).
[5] S. Vandenhaute, T. Braeckevelt, P. Dobbelaere, M. Bocus, and V. Van Speybroeck, “Rare Event Sampling using Smooth Basin Classification,” arXiv [physics.chem-Ph], (2024).
[6] G.M. Torrie, and J.P. Valleau, “Nonphysical sampling distributions in Monte Carlo free-energy estimation: Umbrella sampling,” J. Comput. Phys. 23(2), 187–199 (1977).
[7] M. Invernizzi, and M. Parrinello, “Rethinking metadynamics: From bias potentials to probability distributions,” J. Phys. Chem. Lett. 11(7), 2731–2736 (2020).
[8] https://www.plumed.org/doc-v2.9/user-doc/html/masterclass-21-4.html
[9] K. Kamiya, T. Matsui, T. Sugimura, and Y. Shigeta, “Theoretical Insight into Stereoselective Reaction Mechanisms of 2,4-Pentanediol-Tethered Ketene-Olefin [2 + 2] Cycloaddition,” J. Phys. Chem. A 116(4), 1168–1175 (2012).
[10] X. Hu, X. Zhao, X. Lv, Y.-B. Wu, Y. Bu, and G. Lu, “Ab initio metadynamics simulations of hexafluoroisopropanol solvent effects: Synergistic role of solvent H-bonding networks and solvent-solute C-H/π interactions,” Chemistry 29(17), e202203879 (2023).
[11] https://github.com/matlantis-pfcc/matlantis-contrib/tree/main/matlantis_contrib_examples/plumed_well_tempered_metadynamics




