Blog
本記事はPFNでアルバイトをされている馬場凱渡さんによる寄稿です。
はじめに
本記事では、Optuna v4.5 でリリースされた GPSampler の制約付き多目的最適化の機能を紹介します。
ガウス過程に基づくベイズ最適化 (Gaussian process-based Bayesian optimization; GPBO) は、材料科学や機械学習を含む様々な分野で広く利用されています。GPSampler の初期リリースでは、GPBO をシンプルでユーザーが使いやすいように実装して提供することを目的としていました。カーネルや獲得関数などの要素のカスタマイズ性は、Meta Platforms, Inc. が開発する BoTorch や Ax ほど柔軟ではありませんが、GPSampler はより高速に動作し、依存関係も少なく抑えられています。
一方で、初期の GPSampler が対応できる問題設定は限られていたため、さらなる開発が進められました。Optuna v4.2 では不等式制約に対応し(詳細はこちらの記事を参照)、Optuna v4.4 では多目的最適化に対応しました。そして今回 Optuna v4.5 では制約付き多目的最適化に対応しました。
この新機能は、材料科学・機械学習・創薬など、現実的な物理的・実験的制約の下で複数の目的関数を同時に最適化する必要のある多くの分野で有用です。Optuna v4.5 の制約付き多目的 GPBO により、ユーザーはこの機能を容易に利用できるようになり、様々な分野での科学的進展が加速することが期待されます。
本記事では、その使い方を説明し、技術的概要を簡単に述べ、Optuna の他のサンプラーとのベンチマーク結果を示します。
Optuna での GPSampler の使用方法
GPSampler を利用するには optuna と依存関係のインストールが必要です:
$ pip install optuna==4.5.0 # scipy and torch are also necessary for GPSampler. $ pip install scipy $ pip install torch --index-url https://download.pytorch.org/whl/cpu
インストールが完了したら、GPSampler を study に渡すことで簡単に使用できます:
import optuna
def objective(trial: optuna.Trial) -> tuple[float, float]:
x = trial.suggest_float("x", -5.0, 5.0)
y = trial.suggest_float("y", -5.0, 5.0)
c = x**2 + y**2 - 4.0
trial.set_user_attr("c", c)
return x**2 + y**2, (x - 2) ** 2 + (y - 2) ** 2
def constraints(trial: optuna.trial.FrozenTrial) -> tuple[float]:
c = trial.user_attrs["c"]
return (c,)
sampler = optuna.samplers.GPSampler(constraints_func=constraints)
study = optuna.create_study(sampler=sampler, directions=["minimize"] * 2)
study.optimize(objective, n_trials=100)
GPSampler での多目的最適化
獲得関数にはハイパーボリュームの期待改善量 (Expected Hypervolume Improvement; EHVI) の対数を使用しており、これは Daulton ら [1] の式 (1) と Lacour ら [6] のアルゴリズム 2 に基づいています。技術的な詳細については以下の PR を参照してください:
- #6039:ハイパーボリューム改善量を高速に計算するボックス分解アルゴリズムを実装。
- #6052:準モンテカルロ法に基づく log EHVI を実装。
- #6069:GPSampler で多目的最適化をサポート。
この PR にもあるように、ボックス分解アルゴリズムによって log EHVI の時間計算量が改善され、素朴な手法に比べて 6〜800 倍高速になりました。なお、本実装は BoTorch の実装と概ね整合していますが、一部では異なるロジックを使用しています。詳細については該当 PR を参照してください。
GPSampler での制約付き多目的最適化
上述の多目的最適化に加え、GPSampler を J. Gardner ら [3] および M. Gelbart ら [4] の手法に基づいて、不等式制約に対応できるよう拡張しました。ここでは目的関数と制約関数の両方にガウス過程モデルを適用していますが、それらの間の相関は無視しています。詳細については以下の PR を参照してください:
本実装では、候補点の実行可能性を改善確率 (Probability of Improvement; PI) によって評価します。最終的な獲得関数は、EHVI と実行可能性の PI の積としています。
ベンチマーク
GPSampler による制約付き多目的最適化の有効性を確認するためにベンチマークを実施しました。具体的には、(i) 制約を考慮しない多目的 GPSampler(以下、制約なし GPSampler と記述)との比較による制約導入の効果の評価、(ii) Optuna で制約付き多目的最適化をサポートしている TPESampler および NSGAIISampler との比較、を行いました。
ベンチマーク問題。C2-DTLZ2 問題 [5] を利用します。これは制約付き多目的最適化のベンチマークのために、今回新たに OptunaHub に追加しました。詳細については OptunaHub のドキュメントおよび該当 PR を参照し、目的関数および制約関数の定義については元論文 [2, 6] を参照してください。本実験では、目的関数の数を 2、変数の数を 3 としました。
実装詳細。各最適化は 300 トライアル実行し、異なる 5 つの乱数シードで繰り返して標準誤差を計算しました。C2-DTLZ2 問題は決定的(つまり、目的関数にノイズが含まれない)であるため、GPSampler では deterministic_objective=True としました。使用した実装については該当 PR を参照してください。
計算機環境。ベンチマークは Intel® Core™ i9-14900HX プロセッサ(24 コア、32 スレッド、最大 5.8GHz)を搭載した Arch Linux 環境のコンピュータで実行しました。
結果と考察
得られたパレートフロントと制約考慮の有無による効果の分析
図 1 は得られたパレートフロントを示しており、解の分布や質を確認することができます。
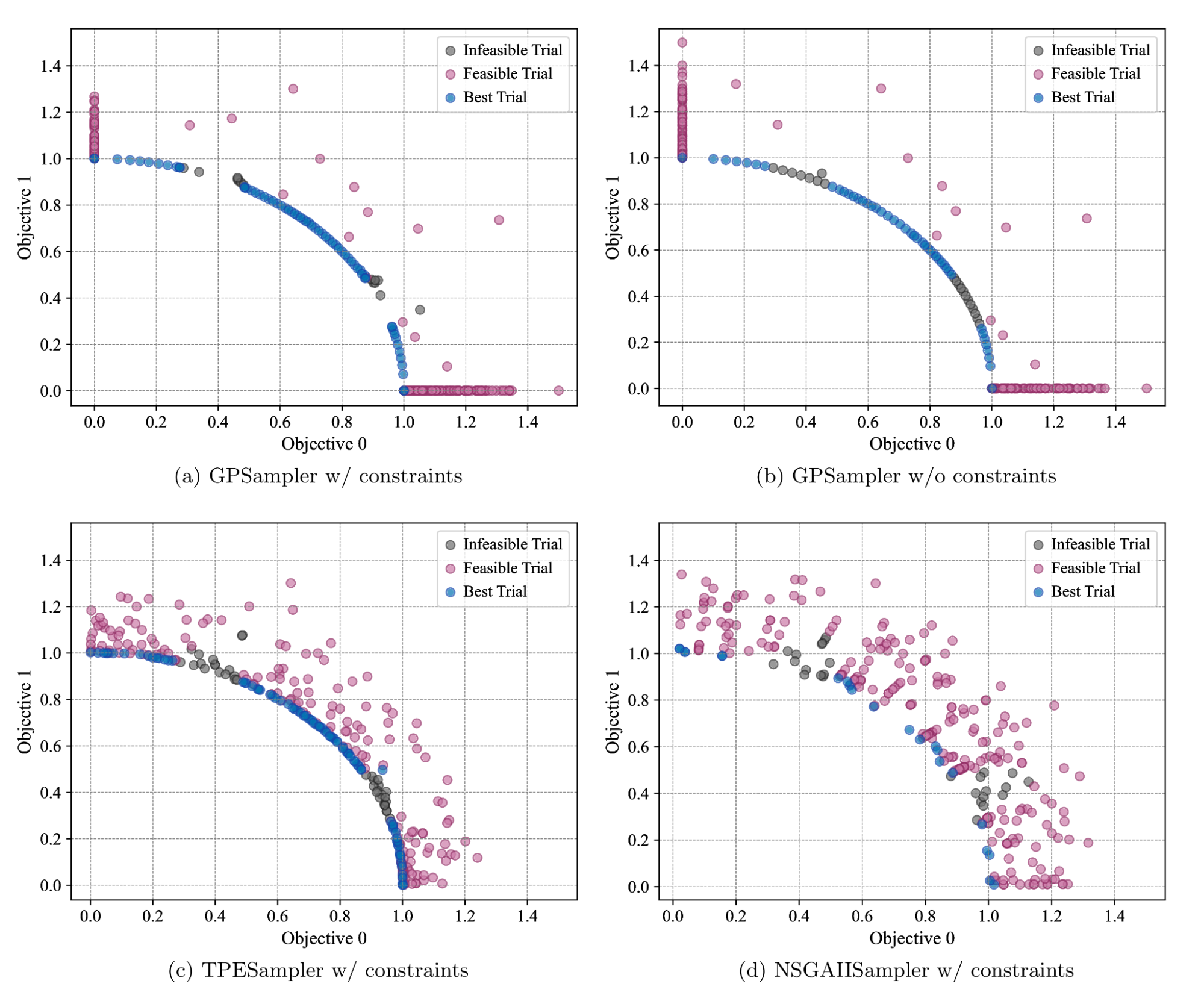
図 1.C2-DTLZ2 問題における 300 トライアル後のパレートフロント。 制約付き GPSampler ((a) に示す) では、制約なし GPSampler ((b) に示す) や TPESampler ((c) に示す) と比べて、実行不可能領域における無駄な評価(灰色で表示)が少なくなっている。一方、NSGAIISampler ((d) に示す) は 300 トライアル後でも依然として収束していない。
GPSampler における制約考慮の有効性
C2-DTLZ2 問題では、分断されているパレートフロントをアルゴリズムが扱う能力を評価できるように、パレートフロント上に実行不可能領域が導入されています [5]。そのため、制約を考慮しなくてもパレート解を得ることは可能ではありますが、そのような方法では実行不可能領域での無駄な評価を多く含んでしまうため、制約付き最適化が重要となります。
制約付き GPSampler (図 1(a)) を制約なし GPSampler (図 1(b)) と比較すると、前者は実行可能なパレート解(青で表示)の間における実行不可能な観測(灰色で表示)が少なく、制約を正しく捉え無駄な評価を削減できていることが分かります。
他のサンプラーとの比較
TPESampler (図 1(c)) と比較すると、GPSampler (図 1(a)) は実行不可能領域における無駄な評価がより少ないことが分かります。一方で、目的変数のどちらかの値が 0 付近の領域については、TPESampler の方がよりしっかりとカバーできています。これは、ガウス過程ベースの獲得関数の性質上、境界付近でのサンプルが過剰になる傾向があること、またその領域における分散が小さくなることにより、その付近のパレートフロントの探索が難しくなるためです。
さらに、図 1(d) に示すように、NSGAIISampler は 300 トライアル後であっても収束に至らず、最適解もほとんど得られていないことから、GPSampler の優位性が確認されます。
実行可能領域でのハイパーボリューム推移の分析
図 2 は実行可能領域でのハイパーボリュームの推移を示しており、各サンプラーにおいて与えられた制約下でどれだけ速く性能が改善されるかを確認することが出来ます。
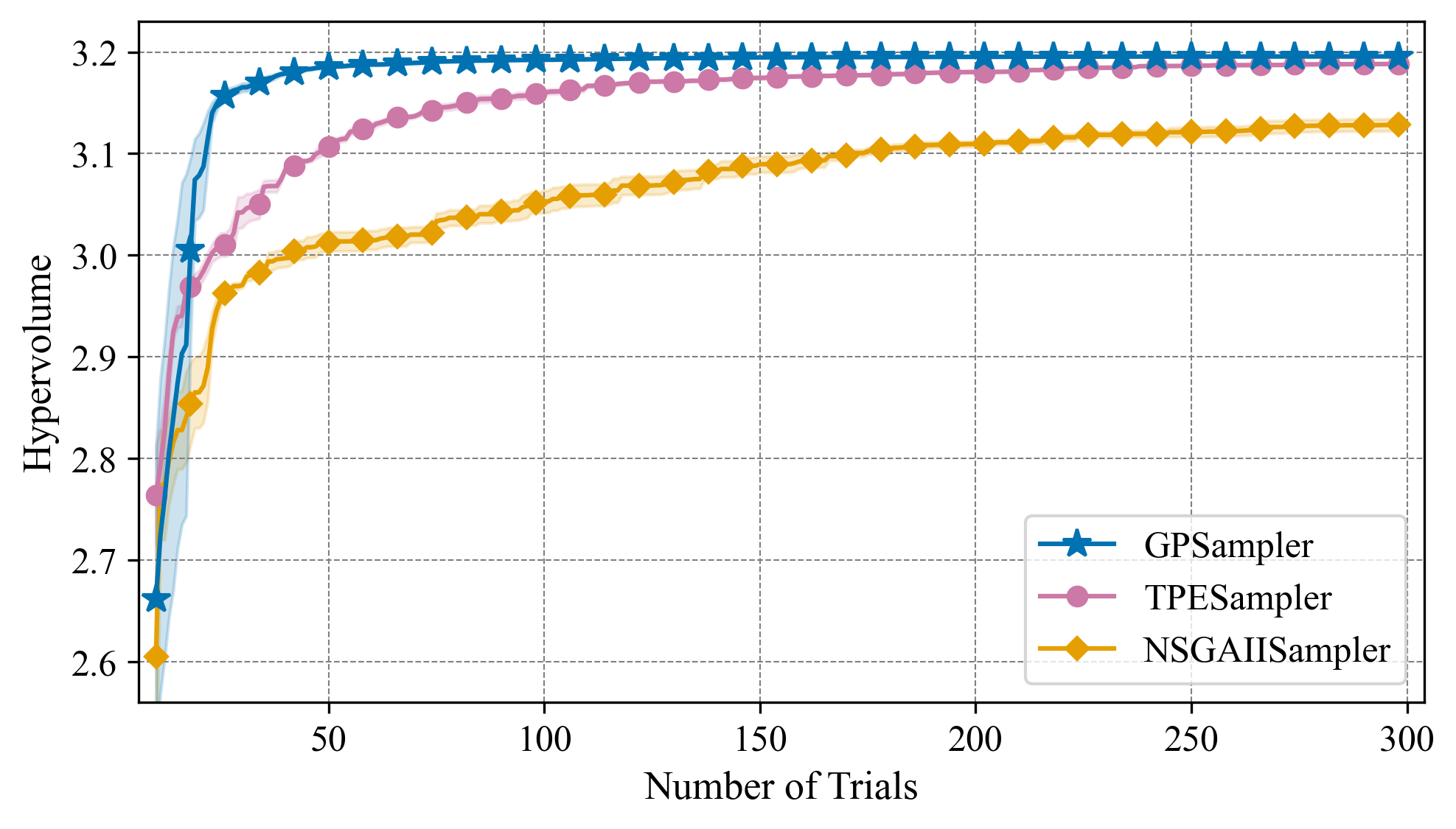
図 2.C2-DTLZ2 問題 [5] における実行可能領域でのハイパーボリューム推移。 実線は平均を表し、半透明の領域は標準誤差を表しており、いずれも異なる 5 つの乱数シードでの実行から計算されています。制約付き GPSampler(青)は、TPESampler(ピンク)および NSGAIISampler(黄)と比べて、より少ない試行回数で高いハイパーボリュームに収束しており、新機能が目的関数の評価コストの削減に有効であることを示しています。
図 2 を見ると、GPSampler のハイパーボリューム推移は、 50 トライアル未満で TPESampler の最終性能に到達し、NSGAIISampler をはるかに早く上回っており、サンプル効率が良いことが分かります。高いハイパーボリュームへの素早い収束は、目的関数の評価が重い場合に特に重要であり、評価の回数が減ることで全体の計算時間が大幅に短縮されます。
終わりに
Optuna v4.5 では GPSampler を拡張し、制約付き多目的最適化をサポートしました。C2-DTLZ2 問題 [5] に対するベンチマークでは、新機能において実行不可能領域での無駄な評価が削減され、TPESampler や NSGAIISampler と比べて高いハイパーボリュームへの収束が高速であることが確認されました。この新機能は Optuna にとって大きな前進であり、計算コストの高いブラックボックス最適化における有力な選択肢となります。ぜひお試しください!
参考文献
[1] Daulton, S., Balandat, M., and Bakshy, E. Differentiable expected hypervolume improvement for parallel multi-objective Bayesian optimization. In Advances in Neural Information Processing Systems, volume 33, pp. 9851–9864, 2020.
[2] Deb, K., Thiele, L., Laumanns, M., and Zitzler, E. Scalable test problems for evolutionary multi-objective optimization. In Evolutionary Multi-objective Optimization, pp. 105–145. Springer-Verlag, 2005.
[3] Gardner, J., Kusner, M., Zhixiang, W., Weinberger, K., and Cunningham, J. Bayesian Optimization with Inequality Constraints. In Proceedings of the 31st International Conference on Machine Learning, volume 32, pp. 937–945. PMLR, 2014.
[4] Gelbart, M. A., Snoek, J., and Adams, R. P. In Proceedings of the 30th Conference on Uncertainty in Artificial Intelligence, pp. 250–259. AUAI Press, 2014.
[5] Jain, H., and Deb, K. An Evolutionary Many-Objective Optimization Algorithm Using Reference-Point Based Nondominated Sorting Approach, Part II: Handling Constraints and Extending to an Adaptive Approach. In IEEE Transactions on Evolutionary Computation, 18(4):602–622, 2014.
[6] Lacour, R., Klamroth, K., and Fonseca, CM. A box decomposition algorithm to compute the hypervolume indicator. Computers & Operations Research, volume 79, pp. 347–360, 2017.
Tag