これらの速度向上は必ずしも全てのユーザにとって必要な改善ではありませんが，Optunaが普及するにつれて多様な使われ方をする内にこれらの速度改善が重要になることがあります．例えば，ニューラルネットワークの学習のように目的関数評価に時間がかかる場合はOptuna自体の速度がそれほど問題となりません．一方で，1 Trialが数秒から数分程度であり，Trialを数千から数万回行いたい場合には速度向上が利便性や最適化における反復回数に直接影響する可能性があります．

今回のブログではOptuna v4.0.0開発で新たに数百から数万Trials程度の効率的な最適化が可能になった多目的TPESamplerについて取り上げようと思います．

なぜ多目的TPESamplerの高速化？

Optunaでは複数の値を返す目的関数の最適化 (多目的最適化) を行うことができます．例えば，翻訳タスクにおける機械学習モデルのハイパパラメータ最適化では翻訳品質 (BLEU等の評価指標) と返答速度 (入力された文章が翻訳されるまでにかかる時間) の両方が重要になります．このようなハイパパラメータ最適化においては多目的最適化を利用することができます．多目的最適化では複数の目的関数のトレードオフを考慮しつつ最適化する都合上，最適解が複数発見されることが一般的でかつ多様なトレードオフを網羅するために単一目的関数の最適化と比較してより多くのTrial数を必要とします．

多目的最適化のTrial数を少しでも減らすために性能のよいSamplerの開発が求められており，Optuna v2.3.0で現状のOptunaの多目的最適化で既定となっているNSGAIISamplerよりも1000 – 10000 Trials程度のベンチマークで高性能を残した (参考: Ozaki et al. [2]のFigs. 8–10) MOTPE [1] (使用法は後述) が導入されました．MOTPEは性能上NSGAIISamplerを上回るとされていますが，今までのOptunaにおける実装ではTrial数が数百以上に増加すると目的関数の評価時間に対して無視できない程度の時間を次のパラメータ提案にかけてしまうという問題があります．

MOTPEが組み込まれているTPESamplerは，多目的最適化のデフォルトSamplerであるNSGAIISamplerにはない，動的探索空間の取扱いやユーザ定義のカテゴリ変数間距離等に代表されるような機能がサポートされているため，MOTPEの高速化は性能面を活かすという目的以外にも大きな意味を持ちます．従って，Optuna v4.0.0ではMOTPEの実装高速化を行うことで，数百以上のTrial数を要する多目的最適化においてもTPESamplerが実用的に動作するように高速化を行いました．今回のブログではTPESamplerのアルゴリズム実装詳細は割愛しますが，興味のある方はMOTPEの論文 [1,2]及びTPEの解説論文 [3]を参照してください．

速度向上のために加えた変更

MOTPEで実行上のボトルネックとなっていたのは，最適なトレードオフの網羅性を定量化するために用いられる超体積の計算 (WFG [4]) とTrialの優劣を決めるアルゴリズム (Non-dominated sortとHSSP (Hypervolume Subset Selection Problem) [5]) でした．ブログでは詳細を省きますが，前述のアルゴリズムの計算量改善，定数倍高速化及びNumPyを用いた大幅な書換を行いました．詳細は以下のPRを参考にしてください．

#5302: Non-dominated sortの定数倍改善 (参考: Watanabe [6]で紹介されているfast-pareto)
#5303: 2次元の超体積計算の計算量改善
#5346: 2次元のHSSPの計算量改善
#5355: HSSPにおける超体積計算の遅延評価による定数倍改善 [7]
#5424: WFGのNumPyによる大幅な書換
#5433, #5591: WFGの定数倍改善

TPESamplerを多目的で使う方法

最も簡単にMOTPEを利用する方法は以下のとおりです．Optunaの多目的最適化では既定アルゴリズムがNSGAIISamplerとなっているため，TPESamplerをstudyに渡さずに多目的最適化を実行するとNSGAIISamplerが利用されることに注意してください．


import optuna


def objective(trial):
    x = trial.suggest_float("x", -5, 5)
    y = trial.suggest_float("y", -5, 5)
    objective_1 = x**2 + y**2
    objective_2 = (x - 2)**2 + (y - 2)**2
    return objective_1, objective_2


sampler = optuna.samplers.TPESampler()
study = optuna.create_study(sampler=sampler, directions=["minimize"]*2)
study.optimize(objective, n_trials=100)

実験

Optuna v4.0.0 (v4.0.0のリリース前のためv4.0.0b0を使用) での高速化効果を見るために前回のリリースとなっていたOptuna v3.6.1のTPESamplerと速度比較を行いたいと思います．実験に使用したコードはGistから確認可能です．尚，今回の可視化に用いた関数はOptunaHubに登録されており，optunahub.load_module(package="visualization/plot_sampling_speed") によって利用可能です．詳細は個別のパッケージページを参照してください．

全ての問題設定において，2次元の探索空間を用いて，各実験で3つの乱数シードを用いて評価しました．各実験は10,000 Trialsもしくは1時間のどちらかに達した時点で終了しました．実行環境として，Ubuntu 20.04, 12th Gen Intel(R) Core(TM) i7-1255UのCPU，Python 3.9.13, NumPy v2.0.0を利用しました．

図1に目的数1–3を用いた実験結果を示します．TPESamplerの原理上，多目的な設定での実行速度は目的数1における実行速度を上回ることができないため，多目的な設定での実行速度を目的数1の線に少しでも近づけることが必要な改善となります．改善限界を示すために図1には目的数1の結果も示しています．また，log (mean of n_trials) = a * log (elapsed_time) + b の係数である (a, b)の線形回帰を用いて，あるTrial数を実行するために必要な実行時間の予測値を破線として描画しました．

図1にある通り，目的数1 (濃青) に関してはOptuna v3.6.1とOptuna v4.0.0で大きな変化はありません．一方で，Optuna v4.0.0で目的数2 (黄緑★) における実行速度が目的数1 (つまり，実装限界値) に拮抗する速度まで向上しています．また，目的数3 (黄★) では実装限界値までの高速化を達成していませんが，大幅に実行速度を改善することができました．例えば，目的数3のときに200 Trialsを提案するのに要する時間が1,000秒以上から3秒となり，300倍近く速くなっています．また，線形回帰の予測に基づくとOptuna v3.6.1で目的数3の設定を1,000 Trials実行する場合，1年以上必要かかることがわかりましたが，Optuna v4.0.0では100秒程度で実行可能になっています．このように1,000 Trialsを超えるような多目的最適化においても高性能なTPESamplerを利用できるようにOptuna v4.0.0の速度改善が行われました．また図2にあるとおり，Optuna v4.0.0では目的数3–5であっても概ね同様の実行速度で動作します．

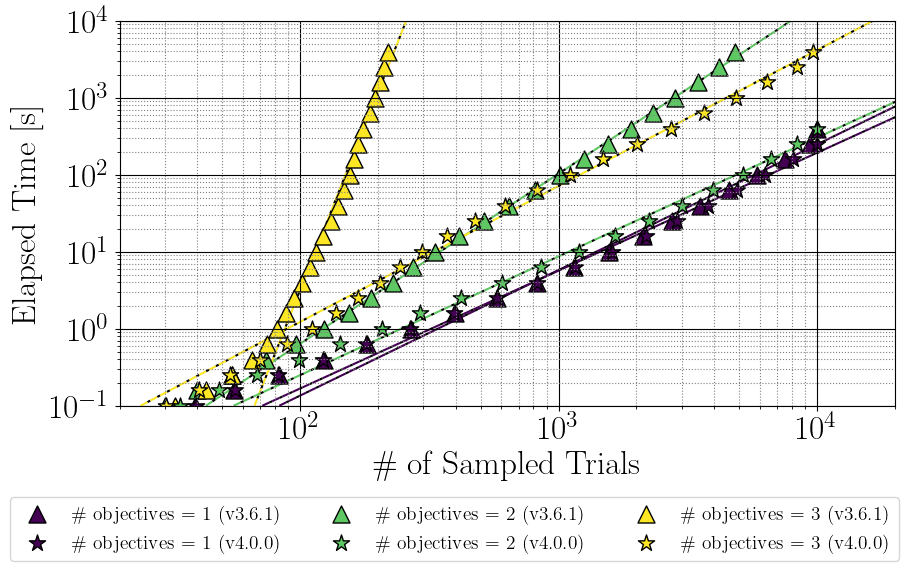
図1. TPESamplerからあるTrial数提案するのに必要な実行時間 (目的数1–3)．横軸はTPESamplerによって提案されたTrial数，縦軸は3回の異なる乱数による実行時間の平均値を示します．★のマーカーがv4.0.0によって得られた結果で，▲のマーカーがv3.6.1によって得られた結果です．破線は実験値を利用した線形回帰から予測された結果です．また，一般的に線が下にあればあるほど，アルゴリズムが高速に動作していることを示します．

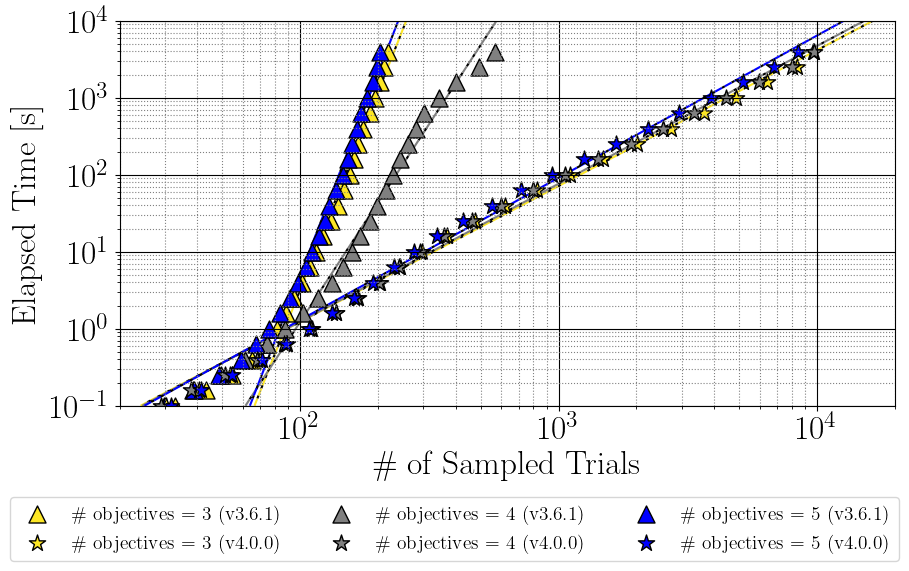
図2. TPESamplerからあるTrial数提案するのに必要な実行時間 (目的数3–5)．図の読み方は図1と同様です．Optuna v4.0.0 (★のマーカー) では目的数3–5それぞれがほぼ同様の速度で動作していることがわかります．

まとめ

Optunaでは継続的に速度改善を行っており，今回はTPESamplerの多目的対応に焦点を当てました．v3系と比較した際にTPESampler による三目的最適化が今回のベンチマークから実測値で300倍程度高速化されたことがわかりました．多目的最適化を行う際にはぜひTPESamplerを利用してみてください．Optuna開発では今後もこのような速度改善を行っていきたいと思います．

Optunaチームでは一緒にOptunaやOptunaHubを開発するパートタイムエンジニアを随時募集しています．また，OptunaHubの機能開発をメインとした短期の募集も開始しました．本記事を通して，ご興味を持っていただけたという方はぜひ下記ページより詳細をご確認ください．

また，8月17日には約2年ぶりとなるOptuna開発スプリントを学生を対象に開催します．Optunaコミッタと一緒にOptunaHub向けの機能開発にチャレンジできるイベントなので，こちらも奮ってご参加ください．

Optuna 開発スプリント #7 / Optuna Dev. Sprint #7 – connpass

参考文献

[1] Yoshihiko Ozaki, Yuki Tanigaki, Shuhei Watanabe, and Masaki Onishi (2020). Multiobjective Tree-Structured Parzen Estimator for Computationally Expensive Optimization Problems. Proceedings of Genetic and Evolutionary Computation Conference (GECCO) 2020.

[2] Yoshihiko Ozaki, Yuki Tanigaki, Shuhei Watanabe, Masahiro Nomura, and Masaki Onishi (2022). Multiobjective Tree-Structured Parzen Estimator. Journal of Artificial Intelligence Research (JAIR) 2022.

[3] Shuhei Watanabe (2023). Tree-Structured Parzen Estimator: Understanding Its Algorithm Components and Their Roles for Better Empirical Performance. arXiv Preprint arXiv:2304.11127.

[4] While Lyndon, Lucas Bradstreet, and Luigi Barone (2011). A Fast Way of Calculating Exact Hypervolumes. Evolutionary Computation 16.1: 86-95.

[5] Andreia P. Guerreiro, Carlos M. Fonseca, and Luís Paquete (2016). Greedy Hypervolume Subset Selection in Low Dimensions. Evolutionary Computation 24.3: 521-544.

[6] Shuhei Watanabe (2023). Python Tool for Visualizing Variability of Pareto Fronts over Multiple Runs. arXiv Preprint arXiv:2305.08852.

[7] Chen Weiyu, Hisao Ishibuchi, and Ke Shang (2020). Lazy Greedy Hypervolume Subset Selection from Large Candidate Solution Sets. Congress on Evolutionary Computation (CEC) 2020.

Area

Data Science / AutoML

Tag

# AutoML

# Hyperparameter Optimization

# Machine Learning

# Optuna