はじめに

7月からOptunaHubという新しいOptuna向け機能共有プラットフォームのベータ版を提供中です。今回は新たに導入されたImplicit Natural Gradient Optimization (INGO) [1]という自然勾配法ベースの最適化アルゴリズムについて紹介します。INGOは進化計算における強力な手法である CMA-ES (共分散行列適応進化戦略) に近いアルゴリズムで、本記事の実験ではCMA-ESよりも良い性能を示しました。

OptunaHubに登録されたINGOアルゴリズム

この節ではOptunaHubに登録したINGOのSamplerを実際に実行してみます。今回の実装はYuhei Otomoさんに協力して頂きました。実装はこちらで見ることができます。

このSamplerの実装にあたり、簡単な単体テストでの動作確認やベンチマーキング結果が論文の主張と整合していることの確認を行いました。下記の図は100次元のL₁-Norm Ellipsoidを用いた比較実験の結果を示したものです。横軸はTrial数で縦軸は目的関数値 (下に行くほど良い) です。実線 (赤: INGO, 青: CMA-ES) が各Trial数までに見つかった最小の目的関数値で、薄い帯のように見えているものは各Trialで見つかった目的関数値の点描画の集合です。なお、帯のように見えるのはTrial数が多く点同士が密集しているためです。論文のFigure 1と同様に、INGOはTrial数を経るごとに着実に改善していますがCMA-ESは途中から上手く改善していないことが見て取れます。

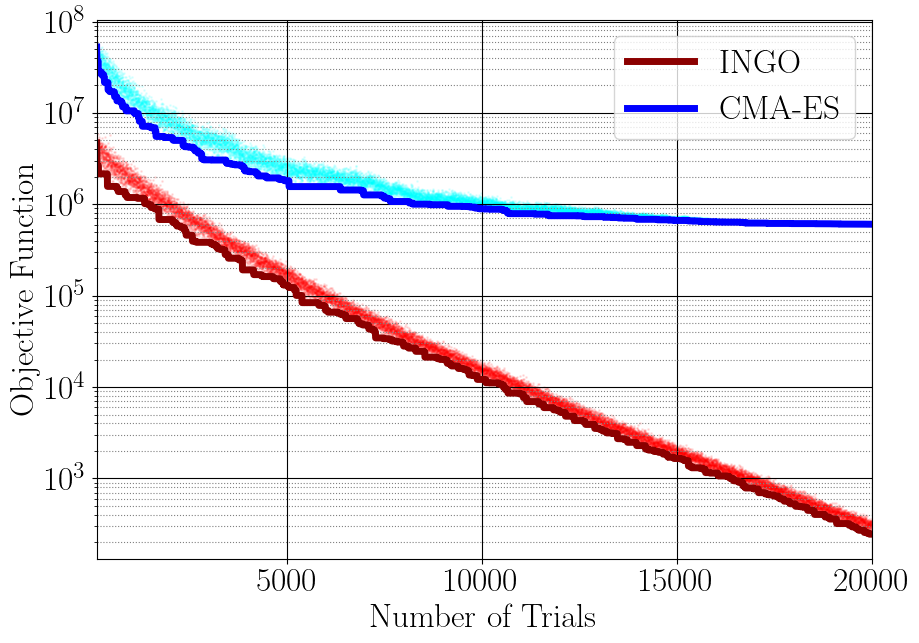
図1. 100次元のL₁-Norm Ellipsoidを用いた比較実験。

ベンチマーキングのために利用したコードは以下の通りです。

from argparse import ArgumentParser

import numpy as np
import optuna
import optunahub

parser = ArgumentParser()
parser.add_argument("--use-ingo", action="store_true")
args = parser.parse_args()


def objective(trial):
    dimension = 100
    X = np.abs([trial.suggest_float(f"x{d}", -10.0, 10.0) for d in range(dimension)])
    coefficients = [10 ** (6 * d / (dimension - 1)) for d in range(dimension)]
    return float(coefficients @ X)


if args.use_ingo:
    mod = optunahub.load_module("samplers/implicit_natural_gradient")
    #`sigma0=0.5` is specified in the paper.
    sampler = mod.ImplicitNaturalGradientSampler(sigma0=0.5, seed=0)
else:
    sampler = optuna.samplers.CmaEsSampler(sigma0=0.5, seed=0)


study = optuna.create_study(sampler=sampler)
study.optimize(objective, n_trials=20000)

このコード (例えば、demo.pyとして保存したものとします) を実行するための依存ライブラリのインストールと実行の手順は以下の通りです。OptunaHubにはINGOのSamplerの他にも様々なパッケージが既に登録されていますが、それらの多くもoptunahubをpip installするだけで使えるようになります！（もちろん、パッケージに個別の指定がある場合は別です。パッケージの著者は依存ライブラリを指定できます）

# 依存関係のインストール。
$ pip install optuna optunahub cmaes

# INGOの実行。
$ python demo.py --use-ingo

# CMA-ESの実行。
$ python demo.py

INGOアルゴリズム解説

Implicit Natural Gradient Optimization (INGO) は目的関数の勾配情報が陽に与えられない条件のもとで最適化 (ブラックボックス最適化) する手法です。LyunとTsang [1] は観測からフィッシャー情報行列を推定することで情報幾何学の有名手法である自然勾配法をブラックボックス最適化に適用できるようにしました。

INGOの関連手法として、Optunaでも利用可能であり、実用的によく用いられる共分散行列適応進化戦略（CMA-ES）があります。両手法ともに探索空間上に定義した多変量正規分布のパラメータ (平均ベクトルと共分散行列のこと) を更新することによって探索領域を決定します。INGOでは自然勾配法によってパラメータを更新し、CMA-ESの場合も一定条件下では自然勾配法のモンテカルロ近似によってパラメータを更新することが知られています [2]。ただし、CMA-ESはあくまで自然勾配法のモンテカルロ近似を利用することから、自然勾配法による最適化手法としてはINGOがより効率的であることが期待されます。本記事の実験と同様に元論文でも連続空間においてCMA-ESに匹敵するベンチマーク実験結果を得たと報告されています [1]。

おわりに

本記事ではOptunaHubにて公開されている自然勾配法ベースの最適化アルゴリズム「INGO」を紹介しました。強力な手法なので、是非皆さんも利用してみてください！

Implicit Natural Gradient Sampler (INGO) | OptunaHub

OptunaHubでは新たなパッケージのPRだけでなく、コードのリファクタリングやバグの報告、欲しいパッケージの提案など、皆さまの様々なコントリビュートをお待ちしています。興味が湧いたらぜひGitHubリポジトリを覗いてみてください。気軽にコントリビュートして、一緒にOptunaHubをより良いものにしていきましょう！

Optunaチームでは一緒にOptunaHubを開発するパートタイムエンジニアを随時募集しています。本記事を通して、ご興味を持っていただけたという方はぜひ下記ページより詳細をご確認ください。

Software engineer (Optuna – Short Term) / ソフトウェアエンジニア（Optuna・短期）/ 株式会社Preferred Networks

参考文献

[1] Yueming Lyu and Ivor Tsang (2020). Black-box Optimizer with Implicit Natural Gradient. arXiv Preprint arXiv:1910.04301.

[2] Youhei Akimoto, Yuichi Nagata, Isao Ono, and Shigenobu Kobayashi (2010). Bidirectional Relation between CMA Evolution Strategies and Natural Evolution Strategies. PPSN, pp. 154–163 (2010).