金融資産におけるリターンの値動きは、しばしばファクターモデルにより説明されます。代表的なファクターモデルの多くが、資産のリターンを「市場に共通する要因（ファクター）」と「資産固有の要因」に分解します。例えば株式市場では、業界（例：小売、半導体）のような「銘柄に共通する市場ファクター」と、各企業の業績などに起因する「企業固有の残渣ファクター」が挙げられます。

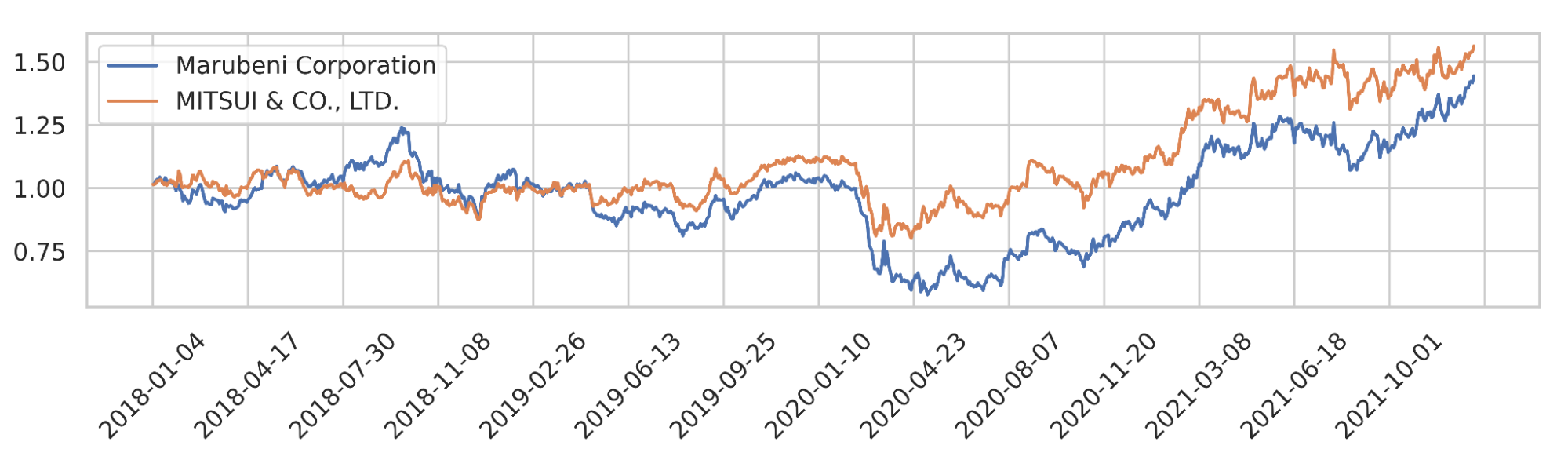
これは、TYO:8002 (丸紅株式会社) とTYO: 8031 (三井物産株式会社) の2018年から2021年の累積リターンです。どちらも「卸売業」に分類されており、類似した値動きを記録している一方で、完全に重なることはなく、企業に固有する動きが確認できます。このような銘柄共通の「市場ファクター」と銘柄固有の「残渣ファクター」を抜き出すことは、効率的なポートフォリオの構成や市場分析をする上で重要です。

ファクター分解のための目標設定

ここで、ファクターを分解するための目標について整理します。「市場ファクター」は各時刻における市場の影響が強く、普遍的な目標を定めることは難しいです。一方で、企業に固有の動きとした「残渣ファクター」は、「銘柄間で独立＝相関が0」であると見なすことができます。そこで、銘柄同士の相関行列の非対角成分を0に近づける変換を目指し、得られるファクターを「残渣ファクター」、残りを「共通ファクター」とします。

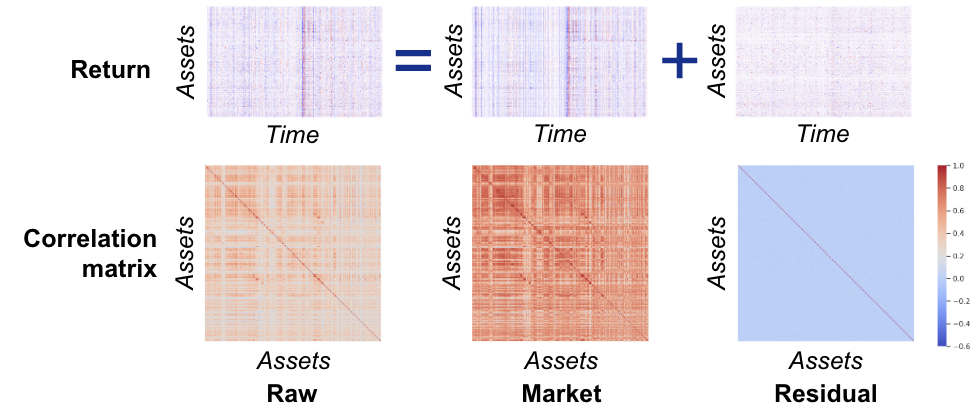
こちらに目標とする操作の概要図を示します。リターン列を市場ファクターと残渣ファクターに分解する際に、残渣ファクターにおける相関行列の非対角成分を0（青色）にする変換の導出を目指します。

先行研究

以上の操作を実現するために有効であると考えられる従来研究について紹介します。

“Determining the Number of Factors in Approximate Factor Models”
- この研究では市場ファクターを抜き出すために主成分分析 (PCA) を利用しています。主成分分析では、リターン列の特異値分解により複数の直交する成分に分解することが可能です。この研究では情報量基準に基づき抜き出す主成分の数を自動で決定し、市場ファクターの動的な抜き出しに成功しています。

“Optimal Whitening and Decorrelation”
- この研究では無相関化する射影を求める手法である「白色化 (whitening)」について包括的に調査しています。今回目標とする残渣ファクターは無相関であることを仮定しているため、白色化の手法は有効なベースラインと考えられます。

“主成分等価法による残差リターン抽出”
- この研究では残渣ファクターを抜き出すために主成分分析と交差検証を組み合わせた手法 (Cross Fitting Diversification; CFD) を提案しています。主成分分析に基づいて残渣ファクターを抜き出す場合、対応する固有値が小さいために推定が不安定となります。この研究では交差検証を導入することで安定した残渣ファクターの抽出に成功しています。

やったこと

先行研究における課題

市場ファクターには、「日経平均株価」などのindexに連動する成分と業種などのセクターに連動する成分が存在しますが、先行研究ではセクターに依存する成分を抜き出せない問題が存在していました。

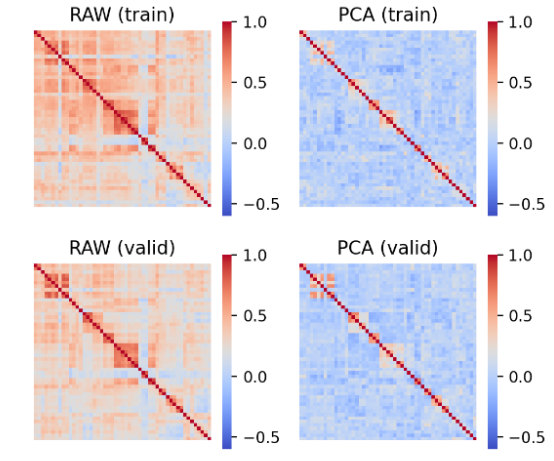
こちらはPCAにより取り出された残渣成分の相関行列です。左側（取り出す前のリターン）では、全体が赤色になっており、全ての銘柄がある程度相関していることが確認できます。一方、左に示すPCAにより取り出された残渣ファクターでは、非対角の成分が青っぽくなっており白色化に成功しています。しかしながら、PCAの残渣ファクターでも対角にブロックのような相関が残っていることが確認できます。ここで、今回の実験では業種毎に銘柄が並べられています。そのため、このブロックの相関は「業種等のセクター内の相関」であると考えられ、市場全体のファクターより小さいファクターが残ってしまう問題が存在しています。

Gaussian Graphical Modelの導入

以上の問題を解消するために、今回のインターンでは、PCAに基づくファクターの抜き出しの後にGaussian Graphical Model (GGM) を導入した階層的な白色化手法を構築しました。金融データにおけるGGMでは、それぞれの銘柄をノードとみなして、ノード間の局所的な関係を推定します。今回、金融時系列は正相関を多く持つという性質を利用するために、MTP2制約を導入したGGMを用いました。一方、GGMで推定できるのはノード間の関係のみで、元のリターンの情報を推定することはできません。そこで、推定した重みを用いてある変数から他の変数へ回帰することで、元のリターンの情報に戻す枠組みを構築しました。PCAによるファクターの抜き出しからGGMによる局所的な関係性を抜き出すまでの一連の操作は一つの線形作用素により表現でき、そのままテスト期間にも応用することが可能です。

PCAに基づくファクターの抜き出し

以降では「残渣ファクター」を抜き出すための変換の導出を目指します。まず、観測されたリターン列を\(\boldsymbol{\mathrm{X}}\in\mathbb{R}^{N \times T}\)とします。ここで、\(N\)は銘柄数、\(T\)は観測された時系列の数を表します。始めにPCAに基づく主要なファクターの抜き出しを行います。\(\boldsymbol{\mathrm{X}}=\boldsymbol{\mathrm{U}}\boldsymbol{\Sigma}\boldsymbol{\mathrm{V}}^{\top}\)を\(\boldsymbol{\mathrm{X}}\)の特異値分解とします。ただし、それぞれの特異値と対応する特異ベクトルは降順に並べられているとします。続いて、\(\boldsymbol{\Sigma}=\mathrm{diag}(\sigma_{1},\sigma_{1},\ldots, \sigma_{M}),\,M=\min(N, T)\)で表される特異値を用いて、各特異値\(k (k=1,2,\ldots,M)\)に対して次式で表される情報量基準を算出します。

\[ IC_{k}=\log(\sum_{i=1}^{M}\sigma_{i}^{2}-\sum_{i=1}^{k}\sigma_{i}^{2})+k\frac{\log (M)}{M} \]

算出された情報量基準が最大となる\(k\)までの特異ベクトルを主要なファクターローディングとみなします。最終的に得られた\(k\)を用いて、PCAに基づく「残渣ファクター」に対応する射影を\(\boldsymbol{\mathrm{W}}=\boldsymbol{\mathrm{I}}-\boldsymbol{\mathrm{U}}_{k}\boldsymbol{\mathrm{U}}_{k}^{\top}\in\mathbb{R}^{N \times N}\)とします。ここで、\(\boldsymbol{\mathrm{U}}_{k}\)は\(k\)番目までの左特異ベクトルとします。ここまでの処理は、“Determining the Number of Factors in Approximate Factor Models”で提案されたものと同様です。

GGMに基づくファクターの抜き出し

続いて、得られた\(\tilde{\boldsymbol{\mathrm{X}}}=\boldsymbol{\mathrm{W}}\boldsymbol{\mathrm{X}}\)にたいしてGGMを適用します。今回適用したMTP2制約下でのGGMでは、次式で表される最適化問題を解きます。

\[ \boldsymbol{\Lambda}=\max_{\boldsymbol{\Lambda}}\left\{\log|\boldsymbol{\Lambda}|-\mathrm{tr}(\boldsymbol{\Lambda}\tilde{\boldsymbol{\mathrm{S}}})\right\}, \hspace{0.5cm}s.t.,\;\boldsymbol{\Lambda}\in\mathbb{M} \]

ここで、\(\tilde{\boldsymbol{\mathrm{S}}}=\tilde{\boldsymbol{\mathrm{X}}}\tilde{\boldsymbol{\mathrm{X}}}^{\top}\)、\(\mathbb{M}\)1は対称M行列の集合で、M行列は非対角成分が非正の正定値行列と定義されます。この問題は射影勾配法で解くことが可能です。得られた\(\boldsymbol{\Lambda}\)をを用いて、GGMに対応する射影を\(\tilde{\boldsymbol{\mathrm{P}}}=\boldsymbol{\mathrm{D}}^{-1}\boldsymbol{\Lambda}, \boldsymbol{\mathrm{D}}=\mathrm{diag}(\boldsymbol{\Lambda})\)と算出します。これは、正規分布における条件付き分布の平均が\(\mathbb{E}[x_{it}|x_{\backslash it}]=-\sum_{j \neq i}\frac{\Lambda_{ii}}{\Lambda_{ij}}x_{jt}\)として求められることに基づいています。以上を用いると、最終的な変換行列は次式のように表されます。

\[ \boldsymbol{\mathrm{A}}=\boldsymbol{\mathrm{P}}\boldsymbol{\mathrm{W}}=\boldsymbol{\mathrm{D}}^{-1}\boldsymbol{\Lambda}(\boldsymbol{\mathrm{I}}-\boldsymbol{\mathrm{U}}_{k}\boldsymbol{\mathrm{U}}_{k}^{\top})\]

実験

設定

データセットとして2016年から2023年までのTOPIX500の銘柄の値動きを用いました。リターンは終値ベースで算出し、2016年1月4日から2022年12月29日までを訓練期間、2022年1月4日から2023年12月28日までを検証期間として、検証期間における白色化の性能に基づき手法の評価を行いました。評価は「非対角成分の絶対値の平均」と「非対角成分の絶対値の標準偏差」により行いました。今回は非対角成分を0にする白色化を目指しているため、両指標とも0に近づくことが望ましいです。

加えて、手法の包括的な評価を実現するために、以下の工夫をしました。1. 訓練の開始期間を2016年1月4日から一年ずつ短くしていき、そのパフォーマンスの変化を記録しました。2. 各訓練期間において、ランダムでサンプリングされた200銘柄において各手法を適用し、それを10回繰り返した平均値を算出しました。

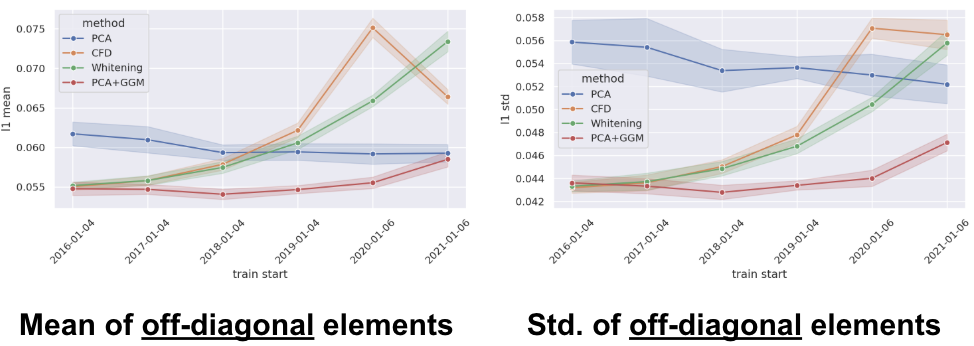
こちらが実験結果です。横軸は訓練の開始期間、縦軸は各評価指標の値を示しています。また、実線が各訓練期間における平均値、薄く色が塗られた領域は±の標準偏差です。非対角成分の平均値では、ほとんど全ての訓練期間において、今回構築した提案手法（PCA+GGM）が最も低い値となっており、高い水準で白色化を実現していることを確認しました。また、非対角成分の標準偏差でも同様に提案手法が最も低い値となりました。比較として用いているPCAや白色化 (Whiteining) は広く用いられている手法ですが、GGMを用いた階層的な枠組みにより、より高精度に白色化を実現できることが示唆されました。ここで、従来研究であるCFDやWhiteningでは、グラフの右側に対応する訓練データ数が少ない条件における精度の劣化が確認できます。これらの手法では、小さい固有値に対応する成分も射影の算出に用いているため、共分散行列がランク落ちする設定において精度が悪化していることが考えられます。一方、提案手法では大きい固有値のみを用いて射影を算出するため、そのような数値的な不安定性の問題を解消することに成功しています。

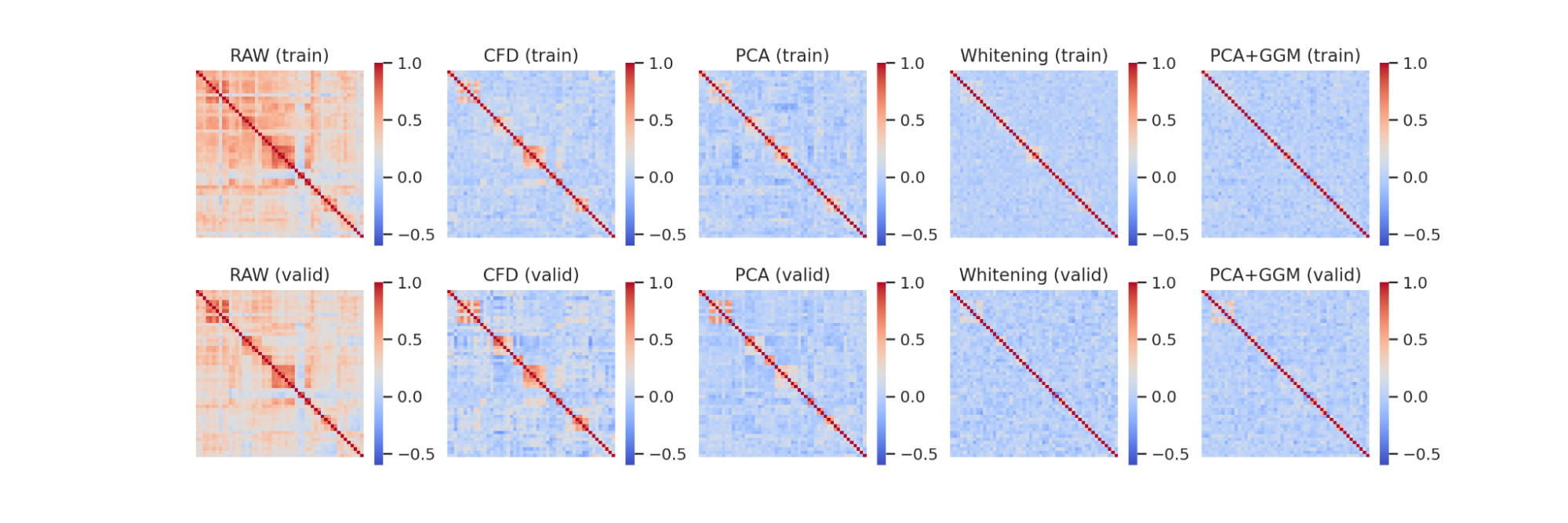
こちらは、実際に算出された残渣ファクターの相関行列の可視化です。CFDやPCA、Whiteningの手法では、左の元の相関行列と比較して白色化できている一方、ブロック毎の相関がでていることが確認できます。一方、一番右に位置する提案手法では、ブロックに発生する相関は概ね確認できません。今回の手法の階層的なアプローチにより、相対的に影響が小さいセクター内の相関が取り除かれ、非対角成分における定量的な結果が改善されたと考えられます。

結論・今後の展望

今回のインターンでは、金融時系列における市場ファクターと残渣ファクターの分解に取り組みました。金融時系列では、インデックス等の影響による銘柄に共通する変動と各企業の業績等の影響による銘柄に固有の動きが存在します。今回構築した手法では、従来研究と比較して精度の良いファクターの分解を実現しました。今後の展望として、今回抽出された残渣ファクターの性質の解析やファクターを用いたポートフォリオの構築が考えられます。