Blog
吉田です。今日も引き続き有名な乱択アルゴリズムということで最小カット問題に対する乱択アルゴリズムを紹介したいと思います。ネタが無くなるということは無いのですが、有名かつ簡単なものとなると、そろそろ終わりが近くなってきているかもしれません。
グラフ\(G=(V, E)\)とは、頂点の集合\(V\)と頂点間を結ぶ枝の集合\(E\)のペアです。
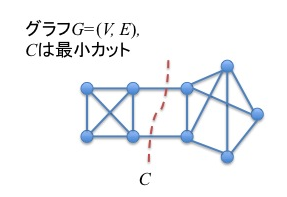
\(G\)のカット\(C \subseteq E\)とは、\(G\)から\(C\)を取り除くと、二つ以上(の連結成分)に分かれてしまうようなもののことを言います。特にカットの中で大きさが一番小さいものを最小カットと言います。恐らく具体例を見た方が良いと思いますので、下の図を見てください。
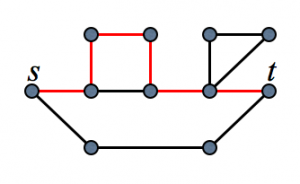
さて「\((s,t)\)-最小カット=\((s,t)\)-最大フロー」という有名な事実が有ります。今回の目的ではないので、余り深入りはしませんが、\((s,t)\)-最小カットとは、グラフ中の頂点\(s, t\)を分けるカットで最小のものを指し、\((s,t)\)-最大フローは\(s\)から\(t\)に流れる”フロー(流れ)”で最大のものを指します。
\((s,t)\)-最大フローを求める決定性アルゴリズム(乱数を使わないアルゴリズム)はよく研究されていて、今現在最速なものは\(O(nm \log(n^2/m))\)です(Hao-Orlin)。ここで\(n=|V|\)は頂点の数、\(m=|E|\)は枝の数です。最小カットを求めるには全ての\(s,t \in V\)に対して、\((s,t)\)-最小カットを求めて、その最小のものを取れば良いです。よって\(O(n^3m \log(n^2/m))\)時間で求まります。
また最大フローに頼らないアルゴリズムもいくつか知られていて、例えばMaximum Adjacency Orderingという手法を用いると\(O(nm+n^2\log n)\)時間で最小カットが計算できます(永持-茨木)。見ての通り発案者は日本人です。僕もこういう有名な結果が得られるように努力したいものです。
さて、今回解説しようと思っていたのは、Kargerによる最小カットに対する乱択アルゴリズムです。中心となるアイデアは簡単で、
- 一つ見つけたい最小カット\(C\)をグラフ中で固定する(勿論どこにあるかは分かりませんが)
- 最小カット\(C\)は枝の数が少ないので、ランダムにグラフから枝を選ぶと\(C\)以外の枝を選ぶ確率が高い
- 選んだ枝を”縮約”しても、最小カットの大きさは保たれる。
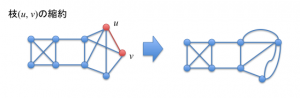
枝\(e=(u,v)\)の縮約とは、\(u\)と\(v\)をくっつけることです。これも正確な定義を見るより、図を見る方が早いでしょう。
縮約に対して以下の補題が成り立ちます。証明は簡単なので考えてみてください。
補題1:
\(G=(V,E)\)をグラフ、\(e\)を枝とする。\(e\)を縮約しても最小カットの大きさは小さくならない。
この事実を元に、次のアルゴリズムを考えます。
Random Contraction
入力: \(G=(V,E)\)
While \(|V|>2\)
枝\(e\)をランダムに選ぶ。
枝\(e\)を縮約する。
残った\(2\)点の間の枝集合を出力する。
まず最初に次の事実を確認します。
補題2:
Random Contractionが出力する枝集合は、元のグラフにおいてカットに対応する。
証明:
最後に残った2点を\(u_1,u_2\)とおく。縮約は頂点をくっつけるという操作なので、\(V\)の分割\(U_1 \cup U_2\)が存在して、\(U_1\)を一点にまとめたものが\(u_1\)、\(U_2\)を一点にまとめたものが\(u_2\)であるとみなすことが出来る。よって\(u_1\)と\(u_2\)の間の枝とは、\(U_1\)と\(U_2\)の間の枝に対応しており、これはカットである。
上の補題からRandom Contractionが出力する枝集合は、常に最小カットの大きさより大きいことが分かります。実際に最小カットに一致する確率を次の補題で見積もります。
補題3:
Random Contractionは確率\(\Omega(n^{-2})\)で、最小カットを出力する。(\(\Omega(n^{-2})\)は\(n^{-2}\)の定数倍以上であることを表します。)
証明:
\(G\)の最小カット\(C\)を一つ固定する。\(C\)の枝が最後まで縮約されない確率が\(\Omega(n^{-2})\)以上であることを示す。\(n=|V|\)を頂点数、\(c=|C|\)を最小カットの大きさとする。
まず最初の縮約を考える。\(G\)の最小カットの大きさが\(c\)であることから、全ての頂点の次数(その頂点に隣接する枝の数)は\(c\)以上である。よって、\(G\)中には\(\frac{nc}{2}\)本以上の枝が存在する。また\(C\)の枝の数は\(c\)であるので、最初のステップで\(C\)以外の枝が選ばれる確率は、少なくとも\(1-\frac{c}{nc/2}=1-\frac{2}{n}=\frac{n-2}{n}\)である。
もし\(1\)から\(i-1\)ステップ目まで\(C\)の枝を縮約しなかっとして、\(i\)ステップ目で\(C\)の枝を縮約する確率を考える。グラフの頂点数は\(n-i+1\)になっている。また、最小カットの大きさは補題1から\(c\)以上である。よって同じ議論を用いて、\(i\)ステップ目で\(C\)以外の枝が選ばれる確率は、少なくとも\(1-\frac{2}{n-i+1}=\frac{n-i-1}{n-i+1}\)。
よって、最後まで\(C\)の枝が選ばれない確率は
\(\frac{n-2}{n}\cdot \frac{n-3}{n-1}\cdots \frac{2}{4}\cdot \frac{1}{3} = \frac{2}{n(n-1)} = \Omega(n^{-2}).\)
最終的なアルゴリズムは次のようになります。
Random Min Cut
入力:\(G=(V,E)\)
\(O(n^2)\)回Random Contractionを実行する。
得られたカットのうち大きさが最も小さいカット\(C\)を出力する。
一回のRandom Contractionで最小カットが得られる確率が\(\Omega(n^{-2})\)以上であることと、Random Contractionは最小カットより小さい枝集合を出力しないことを利用すると、上のアルゴリズムが最小カットを出力する確率は\(\frac{2}{3}\)以上に出来ることが示せます。また、一回のRandom Contractionは\(O(n^2)\)時間で実装出来るので、Random Min Cut全体の計算量は\(O(n^4)\)時間となります。
Random Contractionで最小カットを見つける確率を下げているのは、頂点数が小さい時です。なので頂点数が小さい時は何回も縮約を試し、頂点数が大きい時は荒く試すという方法で、最小カットを見つける確率を上げることが出来ることが知られています。具体的には先ほど\(\Omega(n^{-2} )\)だった確率を\(\Omega(\frac{1}{\log n})\)まで上げることが出来ます。それを利用すると、\(O(n^2\log n)\)時間で最小カットを確率\(2/3\)以上で求めるアルゴリズムを得ることが出来ます。
さてRandom Min Cutが示唆する面白い事実を述べて終わりたいと思います。Random Contractionの証明は、”任意の最小カット”に対して、その最小カットを見つける確率が\(\Omega(n^{-2})\)であると言っています。ある最小カットが見つかるという事象と、別の最小カットが見つかるという事象が同時に起こることはあり得ないので、これはつまりグラフの最小カットの数が\(O(n^2)\)で抑えられるということになります。
Tag