Blog
エンジニアの楠本です。深層学習で再計算と呼ばれる手法を使って学習時のメモリ消費を削減する研究や実装に取り組んでいるのでその紹介をしたいと思います。
背景
大規模なニューラルネットの学習ではしばしば誤差逆伝播(以下同様)で GPU のメモリ不足に陥ることがあります。
通常、誤差逆伝播ではパラメータについての勾配を求める際に必要な順伝播の計算結果を (途中の計算結果も含めて) すべて覚えた状態で勾配計算を行います。
一方で、例えばコンピュータビジョンの重要なタスクであるセグメンテーションや物体検出では入力画像として高解像度のものがしばしば扱われます。モデルについても高精度を達成するために複雑なネットワーク設計、すなわち層が深くまた中間表現のチャンネル数の多いネットワークが使われることが少なくありません。
このように入力やモデルが巨大である場合には記憶しておくべき途中の計算結果全体が巨大になり、学習中のメモリ不足に繋がります。
GPU のメモリサイズはハードウェアの進歩で大きくなってはいるものの、大規模な学習には足りないことがあります。現状で商用販売されているGPUのメモリは最もハイエンドな Tesla V100でも最大 32 GB であり、大規模な学習ではメモリ不足を回避するためにバッチサイズをかなり小さい値にしなければいけないことがあります。バッチサイズを小さくすることは Batch Normalization で使われる統計情報推定を不正確にし、モデルの精度低下につながることが検出等のタスクで知られています[1]。
メモリ不足は深層学習の根幹的な問題であるため様々な解決方法が試されています。例えば半精度浮動小数点数 (FP16) やネットワークのサイズ削減などはその一例でしょう。しかしこれらは本来学習したいモデルに直接変更を加えることになるため、予測精度を悪化させることに繋がりえます。これから紹介する再計算と呼ばれる手法を使うとモデルの予測精度を変えることなくメモリを削減することができます。この場合、精度ではなく、学習時の計算時間が増えることを引き換えにします。
逆誤差伝播法の復習
ここで少し順番が前後しますが、ニューラルネットの学習方法である誤差逆伝播法について今一度復習します。
ニューラルネットワークは変数と計算の順序関係を示す計算グラフによって表現できます。この計算グラフをどう表現するかはいくつか流儀がありますが、ここでは計算グラフは変数を頂点とするグラフとします。これには入力変数、中間変数、出力変数を含みます。変数から変数の間には直接的な依存関係がある場合に枝が生えているものとします。
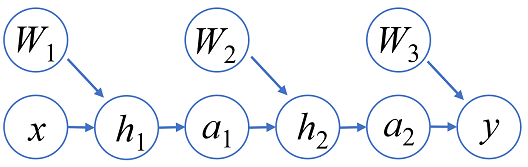
誤差逆伝播法は入力変数(モデルパラメータを含む)に対してその勾配を求めるための方法です。誤差逆伝播法の計算は多変数関数のチェインルールに基づいて計算されます。一般に勾配計算ではネットワークの出力を y として、それぞれの変数 z に対して勾配 ∂y/∂z を求めるのが目的です。これは∂y/∂y=1 から出発して再帰的に勾配を求めることができます。いま、z=f(x) のような関係があるときに ∂y/∂z を表すテンソルがわかっているとすると ∂y/∂x = ∂y/∂z ・ ∂z/∂x = ∂y/∂z ・ F(x) (ここで、F(x) := ∂f(x)/∂x とした) となるため、f に対してその勾配関数 F を事前に計算できる状態にしておけば勾配を計算できます。計算グラフの観点からすると、元の計算グラフ (順伝播部分と呼ぶことにします) から勾配の計算部分(逆伝播部分)を足していることになります。例えば3層のニューラルネットの順伝播部と逆伝播部は以下のような図になります (簡単のため、∂y/∂z を gz のように記しています) 。
再計算
計算グラフは勾配計算のための実行手順を与えてくれますが、これをそのまま実行すると順伝播部分での計算結果は逆伝播時に基本的にすべて必要となるため、単純に中間結果もすべて記憶しておくと、大規模学習ではメモリが足りなくなることがあります。しかしよく考えると順伝播ですべてを記憶せずに一部の中間結果を破棄したとしても、残りの中間結果からもう一度順方向に計算して必要な中間結果を復元さえできれば、逆伝播時に勾配計算を行うことができます。これにより計算のオーバーヘッドが発生する代わりにピーク時のメモリ消費を下げることできます。
このような手法を再計算あるいはチェックポインティング (checkpointing) と呼びます。再計算自体はニューラルネット固有の手法ではなく、自動微分のコミュニティで研究されていました[2][3]。再計算はメモリ消費を抑える代わりに追加の計算時間を発生させます。どの変数をどのタイミングで捨てるかという戦略によってメモリ消費とオーバーヘッドは変わります。近年になってディープラーニングの問題設定に特化した再計算手法が提案されるようになりました[4][5]。
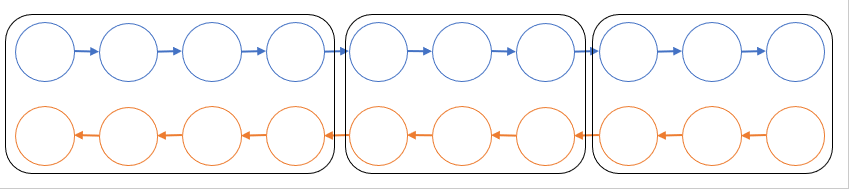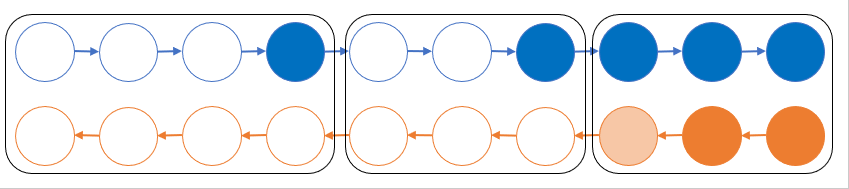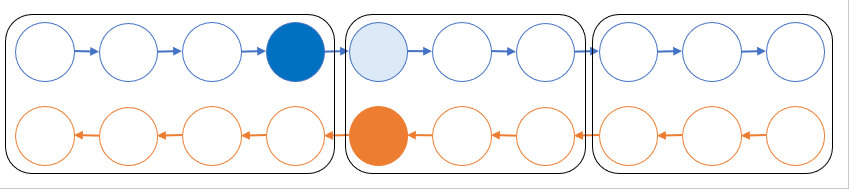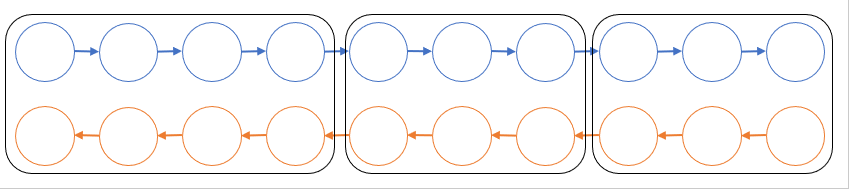
ここではその一つである Chen らの手法 [4] を紹介します。簡単のため、計算グラフが n 層の直線的なネットワークになっている場合を考えます。実際の計算ではモデルパラメータが付いているかもしれませんが一旦無視します。いま、グラフを √n 個ごとに切って √n 個のブロックに分けたとします。順伝播ではそれぞれのブロックを計算した後にブロック間の境界となる部分の変数以外をメモリから捨てることにします。逆伝播では捨てた部分が必要になってしまいますが、残しておいた部分を起点として順伝播のブロックを一時的に復元することでそれぞれのブロック内で逆伝播を実行できます。これにより順伝播部分で再計算のオーバーヘッドが順伝播1回分だけ掛かる代わりに、メモリ消費を O(n) から O(√n) 程度に減らすことができます。ResNet のようにスキップ接続がある場合でも、関節点等でグラフを切れば似たようなことができます。
グラフ的形式化による再計算 (我々の提案手法)
ここからは我々が少し前に arXiv に投稿した論文である “A Graph Theoretic Framework of Recomputation Algorithms for Memory-Efficient Backpropagation” の紹介をします。こちらは2018年夏PFNインターンの井上卓哉さんとの研究成果でもあります。
深層学習で知られている再計算手法は適応可能範囲が計算グラフが限定的で、やや砕けた表現をすると「グラフが直線っぽい場合」に特化していました。しかし近年着目されているネットワークには U-Net のように大きなスキップ接続が存在したりして多様な構造を持っています。また、メモリと計算時間について良いトレードオフを取るという点も大事です。つまりメモリ不足がそこまで深刻でない状況ではできるだけオーバーヘッドを少なくするような再計算スケジュールを求めたいはずです。
そこで我々の論文では、任意の構造の (静的な) 計算グラフ *1 と利用可能なメモリ容量が与えられたときに、メモリ容量を超えない範囲でできるだけオーバーヘッドを小さくするスケジュールを求める離散的な最適化問題を考えます。
任意のグラフに対する再計算も、Chen らの手法の核である「グラフをブロックごとに切ってそれぞれのブロックごとに順伝播、再計算、逆伝播を行う」という考えを拡張できます。すなわち、元の計算グラフの頂点集合 V を V1, V2, …, Vk というブロックに分割し、V1→V2→…→Vk と順伝播計算するものだとします。するとこのような分割方法に対してそれに付随する再計算方法も自然に定まります。砕けた言い方をすると、順伝播で各ブロックを計算し終えた後には境界となるところをだけを覚えて、そうでないところは捨て去るようにします。逆伝播では忘れたところを復元します。よって分割方法を決めればそれに付随する自然な再計算方法の消費メモリとオーバーヘッドが定まります。
分割方法は残念ながら指数的に多く存在するので全探索などはできそうにないですが、もし分割列の途中状態の集合 (V1∪…∪Vi) としてありうるパターン数が少ないのだとすると動的計画法によって最適化問題の解を用いて求めることができます。パターン数が多いときでも、近似的に解くことで現実的に性能の良い解を求める方法も提案しています。
実験では PSPNet, ResNet, DenseNet, U-Net などのネットワークに対して提案手法を用いると計算時間が1.3~1.4倍程度になる代わりに40%-80%のメモリ削減を実現できることや、メモリに余裕がある場合には既存手法よりも計算時間のオーバーヘッドを小さくできることを確認しています。
*1 RNN のようなループを含む計算グラフであっても、ループ回数がイテレーションごとに固定であればループを展開して静的なグラフとみなせます。
Chainer-compiler 上での実装
まだ実験的な段階ではありますが、再計算手法を Chainer の学習で使えるようにする取り組みをしています。再計算では事前に計算グラフの構造が分かっている必要があるため、Chainer 本体ではなく計算グラフのコンパイラである Chainer-compiler 上でその実装を進めています。学習させるときの流れは以下のようになります。
- まず Python で記された Chainer のモデルを静的な計算グラフとして ONNX 形式にダンプします。これは ONNX-chainer を使えばできます。
- ONNX 形式の計算グラフを Chainer-compiler に渡すと学習のための逆伝播部分を足して勾配計算を実行可能な形式にします(Python からは `chainer.Chain` でラップされた状態で見られます)。オプション次第で再計算を含めたスケジュール生成を自動で行います。
Chainer-compiler には Python ラッパーがあり、元の Python コードに少し変更を加えるだけで使えるような形になっています。もし試してみたい方がいらっしゃったらドキュメントの Train your model with chainer-compiler を参考に実行してみてください。
まとめ
深層学習における再計算という手法の紹介と PFN での取り組みについて紹介しました。メモリ不足が深層学習研究開発のボトルネックにならない世の中が来ると素敵なのかもしれません。
ちなみに手動スケジューリングでいいのであれば、Chainer なら functions.forget を使うと比較的カジュアルに再計算ができます。
文献
[1] Chao Peng, Tete Xiao, Zeming Li, Yuning Jiang, Xiangyu Zhang, Kai Jia, Gang Yu, and Jian Sun. MegDet: A large mini-batch object detector. In IEEE Conference on Computer Vision and Pattern Recognition (CVPR), pages 6181–6189, 2018.
[2] Andreas Griewank and Andrea Walther. Evaluating derivatives: principles and techniques of algorithmic differentiation. Vol. 105. Siam, 2008.
[3] Benjamin Dauvergne and Laurent Hascoët. The data-flow equations of checkpointing in reverse automatic differentiation. International Conference on Computational Science. Springer, Berlin, Heidelberg, 2006.
[4] Tianqi Chen, Bing Xu, Chiyuan Zhang, and Carlos Guestrin. Training deep nets with sublinear memory cost. arXiv preprint, arXiv:1604.06174, 2016.
[5] Audrunas Gruslys, Rémi Munos, Ivo Danihelka, Marc Lanctot, and Alex Graves. Memory-efficient backpropagation through time. In Advances in Neural Information Processing Systems (NIPS), pages 4125–4133, 2016.