Blog
本記事は、2019年インターンとして勤務した服部桃子さんによる寄稿です。
こんにちは、2019年度PFN夏季インターン生の服部桃子と申します。
私は今回のインターンで、Chainerを用いてニューラルネットワークを記述しているPythonスクリプト中の式の型とshapeを “半”静的に推論するというプロジェクトに取り組みました。
なお以下の話のより詳細な内容については、6/15から開催される国際会議 PLDI 2020 (ACM SIGPLAN Programming Language Design and Implementation) 併設のワークショップ MAPL 2020 (the 4th Annual Machine Learning and Programming Languages Workshop) で発表してきます。
PLDIはプログラミング言語の設計と実装に関する最高峰の国際会議の一つであり、MAPLは2017年よりPLDIに併設で開催されている、プログラミング言語分野と機械学習分野のコラボレーションを目指したワークショップです。
今年はオンライン開催ですが、参加される方はよろしくお願いします。
Semi-static Type, Shape and Symbolic Shape Inference for Dynamic Computation Graphs
動機
このプロジェクトのモチベーションは2つあります。1つは、推論された型情報を(chainer-compilerによる)モデルのコンパイル時に利用するため、もう1つは、プログラムの静的な型付けによって典型的なバグの検出を実行前に行うため、です。
chainer-compiler (elichika)
PFNでは昨年に、chainer-compilerという実験的なプロジェクトがありました。
このプロジェクトの目指しているところについてはメンターでもあるPFN社員浜地さんによる記事で詳しく解説されています。
chainer-compilerのコンポーネントの1つとしてelichikaというものがあり、Pythonの抽象構文木を拡張されたONNXフォーマットに変換しています。この変換を正しく行うため、またその後の最適化等でONNXフォーマットに型情報が必要となるため、変換の際に与えられたモデルの計算グラフ中に出現する式の型をelichika内で推論する必要がありました。ここで必要とされている型とは、Pythonのプリミティブな型(int, float, list等)およびテンソル(numpy.ndarray, chainer.Variable等)のdtypeなどを指します。
テンソルのshape問題
Pythonで機械学習のプログラムを書いていてテンソルのshapeが途中で合わなくなってしまい、とりあえずprintで変数のshapeを出力してデバッグをするという作業をした経験は多くの方がお持ちだと思います。
与えられたプログラム中に出現するテンソルのshapeだけを計算して手軽にチェックすることができれば、このような辛い作業をする必要がなくなります。
このため今回のプロジェクトでは、elichikaで必要とされているレベルの型にとどまらず、テンソルのshapeや次元(ndim)も推論していくことを視野に入れていました。
なお同様のモチベーションを持っているプロジェクトの1つに、pythonの静的型チェッカであるmypyのnumpy拡張がありますが、そこで実装されている型にさらにdtypeやshapeの情報を含んだものを扱いたかったため、独自に開発を進めました。
問題設定と成果
タイトルに“半”静的な推論と書きましたが、今回のプロジェクトにおける型推論は前提条件がかなりユニークです。具体的には、通常の静的型付けコンパイラにおける型推論と次のような点で異なります:
- 機械学習のモデルを表すクラスのインスタンスが既に存在していて、
そのメソッドに対して推論を行う- 特に、クラスのアトリビュートの情報を値として持っている
- メソッドの引数の値(と型)がわかっており、
その引数に応じてメソッド内の各式につく型を得たい - ユーザ定義関数の呼び出しはインライン展開するため、
多相型を考える必要がない(呼び出し元ごとに型をつければ良い)- 再帰関数は考慮せず、展開は必ず止まると仮定する
- chainerやnumpyの関数は引数の値によって出力の型やshapeが変わるものが
多くあるため、関数適用の際の引数は(定数であれば)なるべく評価したい
このため型推論というよりは、プログラムを型とshapeに関わる部分だけ評価していくというイメージになります。
実際の例として次の図のようなプログラムを見てみましょう。Modelクラスのインスタンスを作り、forwardの引数にくる値の型が
x : numpy.ndarray(dtype=float32, shape=(2, 3, 227, 227))
t : numpy.ndarray(dtype=int32, shape=(2, 57, 57))
となるようにしてforward(x, t)に対して型推論器を実行すると、forward 中の全ての式に上から順に型がついていきます。例えば2行目の左辺のhの型は、
h : chainer.Variable(dtype=float32, shape=(2, 64, 57, 57))
であると推論されます。
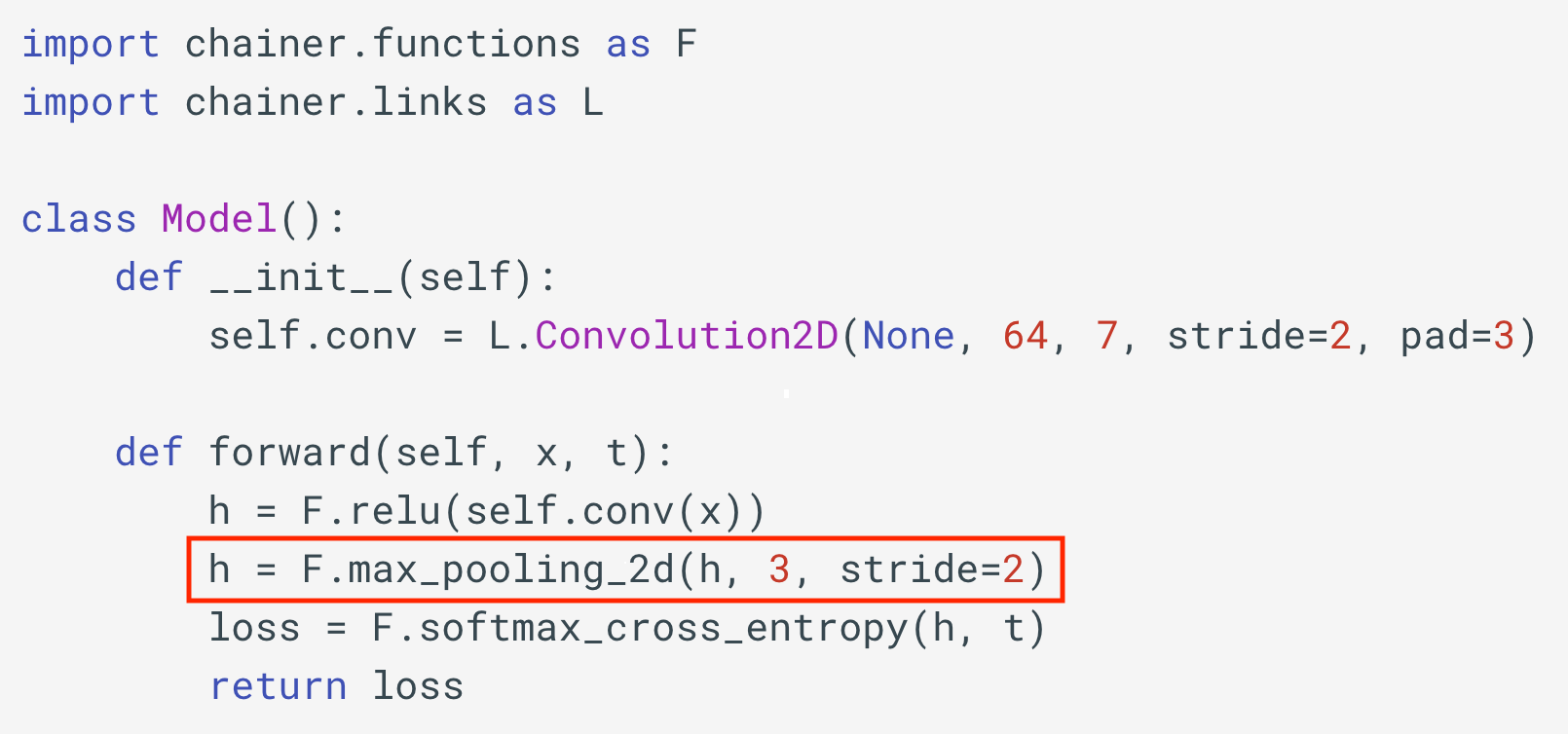
もちろんこれよりももっと複雑で現実的なネットワークに対しても型推論器を動かすことにも成功しており、インターン期間中にはGoogLeNetやEspNetなどに対する型とshapeの推論を達成しました。
またshapeの推論を発展させて、次のようにsymbolicにshapeを表現する機能も実装しました。
次の図は上のプログラムと同じですが、引数のxに型アノテーションがあり、shapeの一部の要素に名前がつけられています。このとき、forward内のテンソルの各式につくshapeは、型アノテーションで使用されている名前を変数とする数式として表示させることができます。すなわち、先ほどと同様の入力で型推論器を実行させたとき、例えば2行目の左辺のhのshapeは
(2 (bsize), 64, 57 (ceil(((height - 1) // 2 - 2) / 2) + 1), 57 (ceil(((width - 1) // 2 - 2) / 2) + 1))
のように、推論された実際の値に数式を伴って出力されます。

また、今回の型推論器はプログラムを実行しないため、時にはshapeが完全にはわからないこともあります。推論できなかったshapeの次元には None を入れていますが、 None の入った不完全なshapeに対しても、残りのわかっている情報を元に推論できるshapeは全て推論するという方針を取っています。
例えば下のように、 x.shape[3] がわからなくなってしまっているとき、 x に対してpoolingをして得られる y のshapeを考えます。 y.shape[3] は x.shape[3] に依存するのでわかりませんが、そのほかは推論できています。
# x.shape: (2, 3, 227, None)
y = F.average_pooling_2d(x, ksize=3, stride=2)
# y.shape: (2, 3, 113, None)
shape推論のメカニズム
型推論器の中では、shapeの各要素は ShapeElem というクラスで表現され、このクラスはそれが表すvalue (intの値または None)と、valueの計算履歴を保持するAST(Abstract Syntax Tree)を持っています。
ShapeElem を含む算術演算( __add__ 等)はオーバーロードされて ShapeElem を返すようになっており、片方にvalueが None であるような ShapeElem がきたら結果の ShapeElem のvalueも None になります。イメージとしては次のような感じです。
ShapeElem(None) + ShapeElem(4) = ShapeElem(None)
ShapeElem(3) * ShapeElem(None) = ShapeElem(None)
これによって、shapeの計算時に失敗を伝播させることができます。
また、演算子のオペランドのvalueが両方ともintの値であるときは、(a)結果のvalueを計算しながら新しいASTを構築し、(b)可能であればASTの簡約を行います。

なお、テンソルの和をとるときなど、複数のテンソルのshapeの同一性をチェックする際は、ASTではなくvalueを比較します。変数を含む代数的な式の同一性の検証は一般には困難ですが、ASTとともにvalueを持ち回ってvalueで比較をすることによってこの問題を回避しています。
まとめと今後の課題
若干の実行時情報をもとに、入力のPythonプログラムの型とshapeのみを計算するプログラムを作成し、shapeのsymbolicな型アノテーションという興味深い機能も実験的に実装してみました。なお成果は全てchainer-compilerのmasterブランチにマージされているのでよければご覧ください。
今回の実装ではshapeの要素をsymbolicな式と具体的な値のペアで扱いました。理想的には値を持つ必要をなくしてsymbolicなままで扱うことができれば、特定の入力値に依存することなくshapeの整合性をチェックすることができ、プログラムの信頼性が上がります。ただしそのためにはsymbolicな式の同一性を証明する必要がありますが、shapeのsymbolicな式はネットワークによってはかなり複雑になるため、この証明を完全に自動で行うのは理論的には困難であると予想されます。完全な証明のかわりにテストを用いて擬似的に同一性を判定するなどの解決策が考えられますが、今後の課題として興味深い問題だと思います。
最後になりますが、このプロジェクトを通じてお世話になった以下の方々に心から感謝を申し上げます。
- インターン期間中から論文執筆まで共著者として関わってくださった、
メンターの澤田さん、副メンターの浜地さん、酒井さん、清水さん - インターン終了後の型推論器の開発を支えてくださった
Chainer compilerチームの渡辺さん - 投稿前の論文を読んでコメントをくださった山崎さん
- インターン期間中にお話してくださったPFNの全ての皆様
今回、2ヵ月という短いインターンの期間の中で、ゼロからpythonの半静的推論の機能を開発していただきました。当初の目標はshapeの推論まででしたが、シンボルの表示という予定してなかった機能まで実装し、目覚ましい成果を上げていただきました。そして実装のみならず、論文にまとめて国際会議に採択されました。今回の成果はchainerに限らず、pythonによるテンソルの計算に関連する問題を改善していくと考えています。




