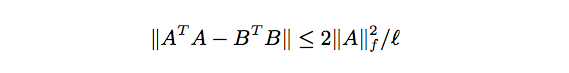Blog
毎日暑いですね。比戸です。
ちょうど今週シカゴで開かれていたSIGKDD2013でBest research paperに選ばれたEdo Liberty氏 (Yahoo! Haifa Labs)の”Simple and Deterministic Matrix Sketching”のアルゴリズムを実装して公開してみました。
元論文PDFは著者サイトから、私が書いたPythonコードはGithubからそれぞれ入手できます。
SIGKDD (ACM SIGKDD Conference on Knowledge Discovery and Data Mining)はACM主催で行われる、知識発見&データマイニングにおけるトップ会議です。最近は機械学習との境目が曖昧になってきましたが、査読時には理論的な新しさだけでなく、実データ(特に大規模データ)を使った実験での評価が必要とされるのが特徴です。
この論文のテーマ、Matrix sketchとは簡単に言うと、元の大きなNxM行列Aを、はるかに小さなℓxM行列B(N >> ℓ)で近似するものです。ここでいう良い近似とは、A^T AとB^T Bの差のノルムが小さいということです。このような行列演算に帰着できるためsketchが有効な応用例としてはPCAやk-meansなどが代表的です。これらは元行列AのSVD(特異値分解)等を用いた低ランク近似でも計算できることはよく知られていますが、行列のサイズが大きすぎる場合、SVD自体のコストが大きくなり過ぎます。そこで、より低い計算量で行列をsketchで直接小さくしてから処理する手法が最近は注目されてきています。
そんな中、この論文の着眼点と貢献は、次のようにまとめられます。元アイデア自体は去年6月の段階でarXiv.orgに公開されていたようで、言及しているブログ記事も見かけます。
- 元行列Aの各行を、各変数の「表現量」ベクトルと見なすと、sketchは直感的にはよく現れる「方向」をできるだけ残して行数を削減する操作として捉えられる
- そのような操作は、各アイテムの出現個数リストからよく現れる共起パターンを見つける、頻出アイテムマイニングと似ている
- 実際、ゼロ行列から始まるsketch行列BにAの各行を挿入しながら、BのSVDを求めて頻出方向を更新しつつ、特異値が小さいものに対応する部分はゼロ行に潰す操作を行って、逐次的にBを更新するアルゴリズムを与えた
- その結果、以下の不等式で近似誤差を抑えられる
Pythonのソースコードでも、NumPyを使えばメインの処理はわずか10行ほどで書けてしまいます。
論文の実験では、行列AがN=10,000、M=1,000くらいのサイズでℓを10から200くらいまで動かすと、sketch行列Bによる誤差が行列Aを直接SVDに書ける場合(Brute force)の精度に近づいていくこと、かつ計算コストが低いままであることが示されています。このデータ規模ではBrute forceと比べた場合の利点をまだ活かしきれてないのではないかと思います。実際には、SVDにも色々な高速化版があるので、実応用での精度と速度の評価が待たれるところです。
さて、せっかく実装してみたので、何か見た目麗しい例を作ってみようということで、有名なUSPS手書き文字認識データセットを使って東大の富岡先生が公開している、PCAを使って得られた主成分2軸が貼る平面上に各数字サンプルをプロットするタスクを真似してみました。
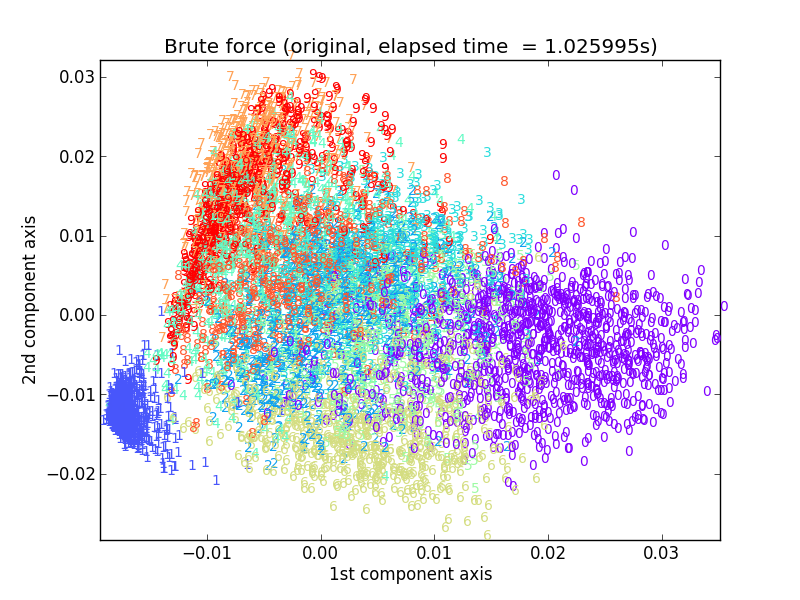
まず、オリジナルのデータ行列(7291サンプル x 256変数)を使ってSVDによる主成分解析をした結果がこちらです。
0と1という画像として見分けやすいもののクラスタが左右に明確に分かれ、その間に他の数字のクラスタが交じり合いながら埋め込まれているのがわかるかと思います。これに一致するものを、sketch行列から作るのが目標です。
ではFrequent-directionsアルゴリズムを動かしていきましょう。やっていることは、いったんℓ x 256のsketch行列を求め、そのSVDから射影行列を作って、元の行列にかけることで、同様の出力を得ています。
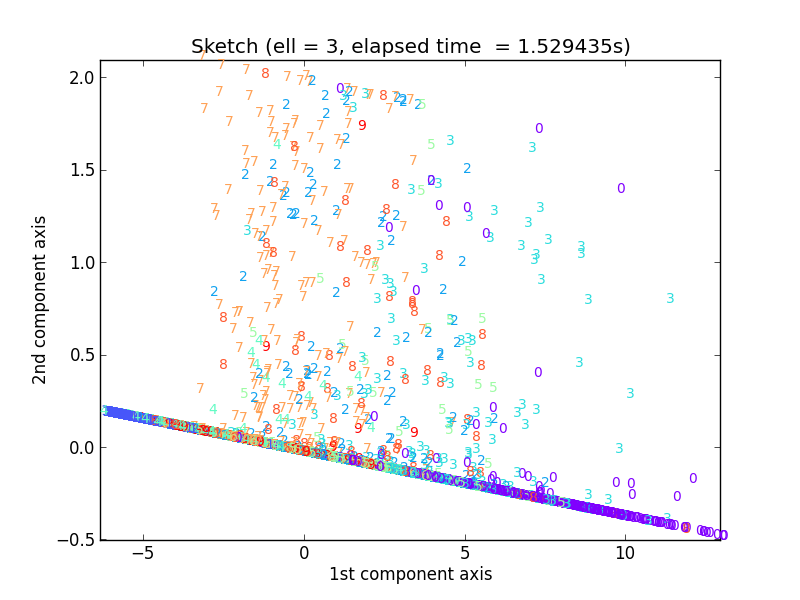
まずはℓ = 3の場合です。
なんとなく、直線上の左側に水色の1、右側に紫の0が固まっている感じはしますが、3 x 256の大きさのsketch行列Bを半分はゼロ行のまま作っていくので、さすがに無理があるようです。
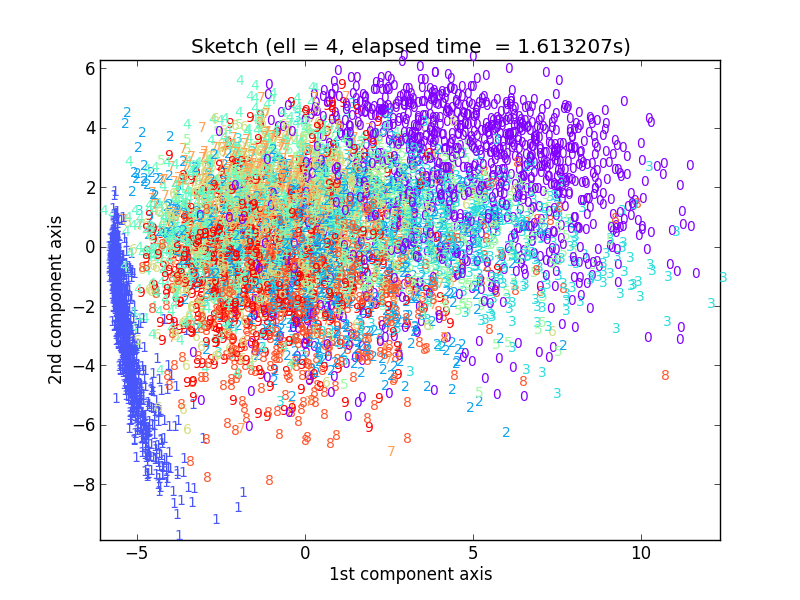
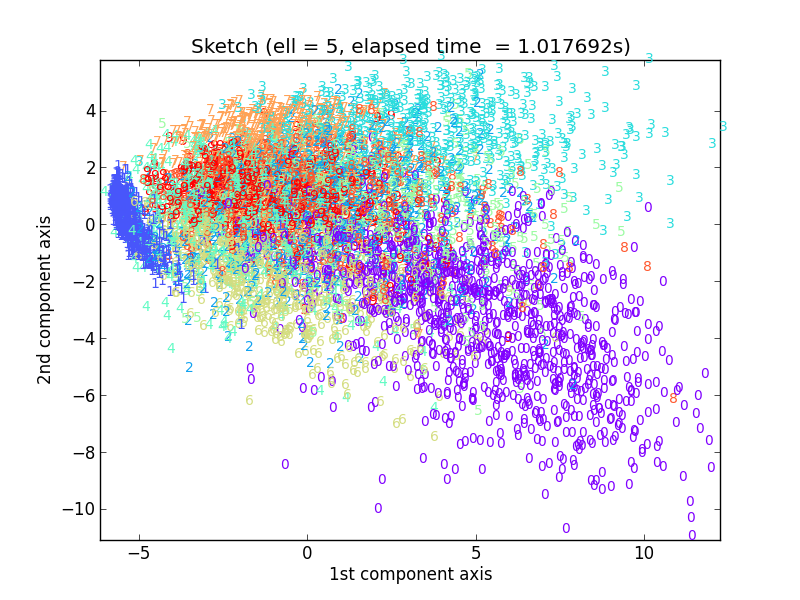
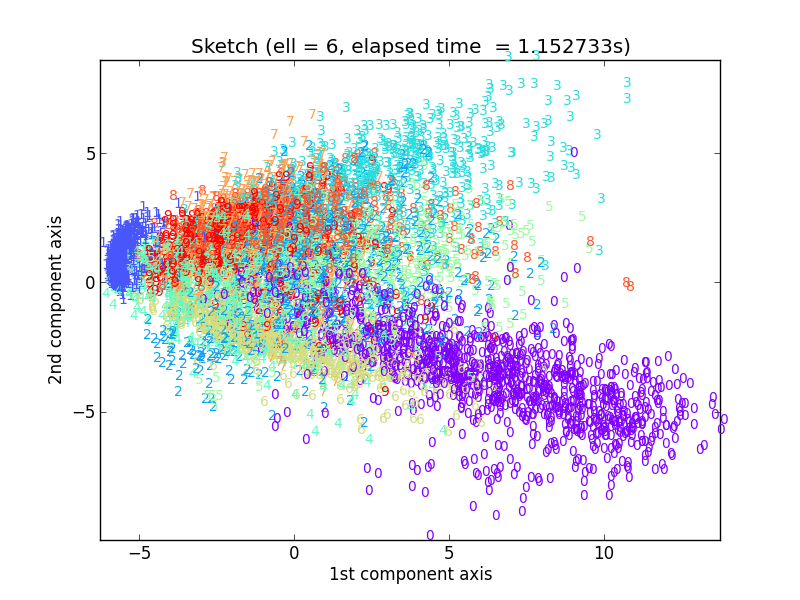
ではℓ = 4, 5, 6といきます。
かなりドラスティックに変わっていますが、だんだん数字ごとのクラスタがはっきりしてきた感じがしますね。しかし元のPCA出力を近似するという意味ではまだまだです。
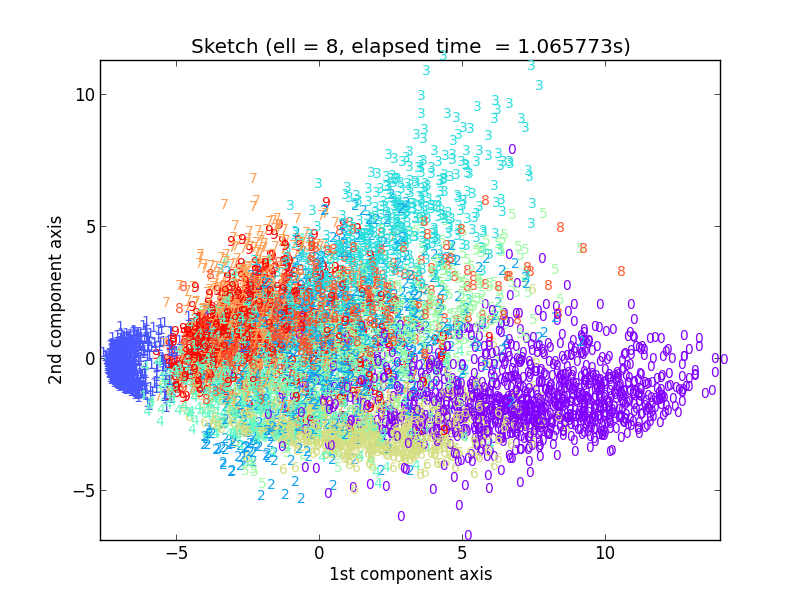
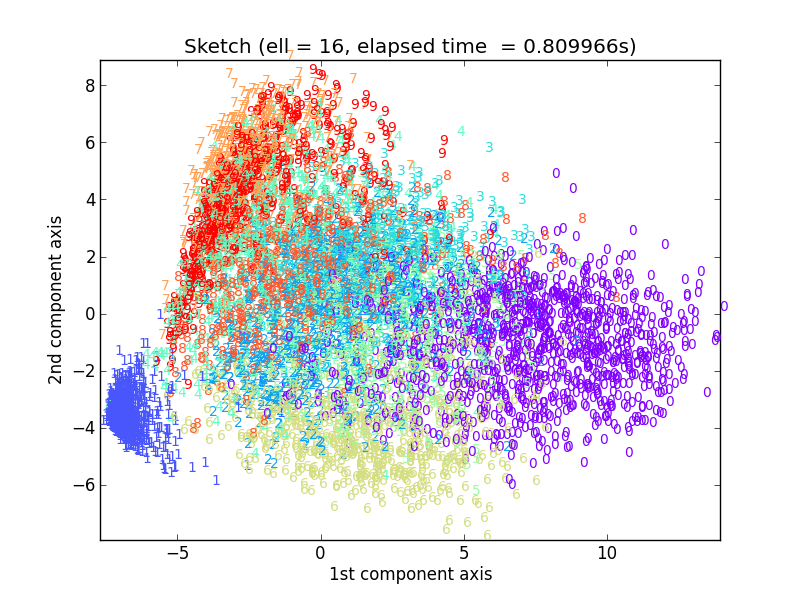
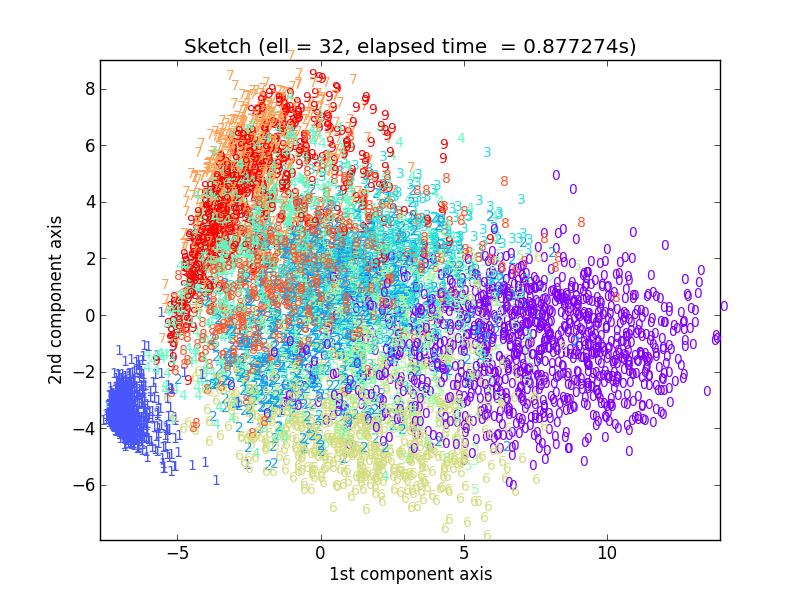
ここからは飛ばし気味にℓ = 8, 16, 32といきます。
おお、ℓ = 16あたりでもうかなりオリジナルの実験結果に近づいてますね。実はℓ = 32で元の出力とほぼ一致していて、それより大きいℓの値で試しても計算時間が大きくなるだけで結果はほとんど変わりませんでした。
この実験から言えることは、7291 x 256の大きさを持つUSPS元データ行列の特徴は、 16 x 256という非常に小さなsketch行列で十分近似できるということです。もともと10種類の数字が含まれていることから、1つ1つの数字を代表するような頻出方向ベクトル(Frequent-directions)があれば十分と予測されるので、このℓ = 8から16に増やしたタイミングでほぼ一致するようになったというのは興味深いです。
こちらのサンプルスクリプトもGithubに上がっていますので宜しければ試してみて下さい。
ちなみに、上記のアルゴリズムは行列Aの各行要素に対して逐次的に実行できるので、データサンプルが1つ1つ得られるような環境で、オンラインで動作させることも可能です。つまり巨大な行列Aをメモリに保持する必要がありません。バッチ処理として考えると、上記のUSPS実験でも速度的なメリットはあまり無いので、なぁーんだと思われるかもしれませんが、メモリ使用量がNではなくℓで抑えられるというのはこのアルゴリズムの非常に大きなメリットだと思います。
さらに、論文の中ではAもBもぶった切ることで並列化が簡単にできることにも触れられています。
ん?オンラインで…並列実行可能な…機械学習と関係ある…?どこかで聞いたことあるようなコンセプトですね!