Optuna GPSampler (ガウス過程ベースのベイズ最適化手法) の 2.5倍高速化

本記事は2025年度PFN夏期インターンシップで、Optuna GPSamplerの高速化に取り組まれた入江海地さんによる寄稿です。

この記事の要約

• Optuna の GPSampler は強力である一方で、Trial 数が増えると実行時間が長くなるため、問題設定によっては、GPSampler の計算時間が課題となります。
• GPSampler のボトルネックの一つは、並列化可能ですが、並列化手法の調査および速度の検証は行われてきていません。
• 本インターンシップでは、並列化手法について、包括的な調査および速度検証を行い、OSS の保守性とユーザー体験を損なわない形で Optuna に組み込みました (#6268) 。
• 今回の成果は Optuna v4.6 以降で利用可能となり、図1にあるように、v4.5と比較して GPSampler が2.0〜2.5倍高速化されます。

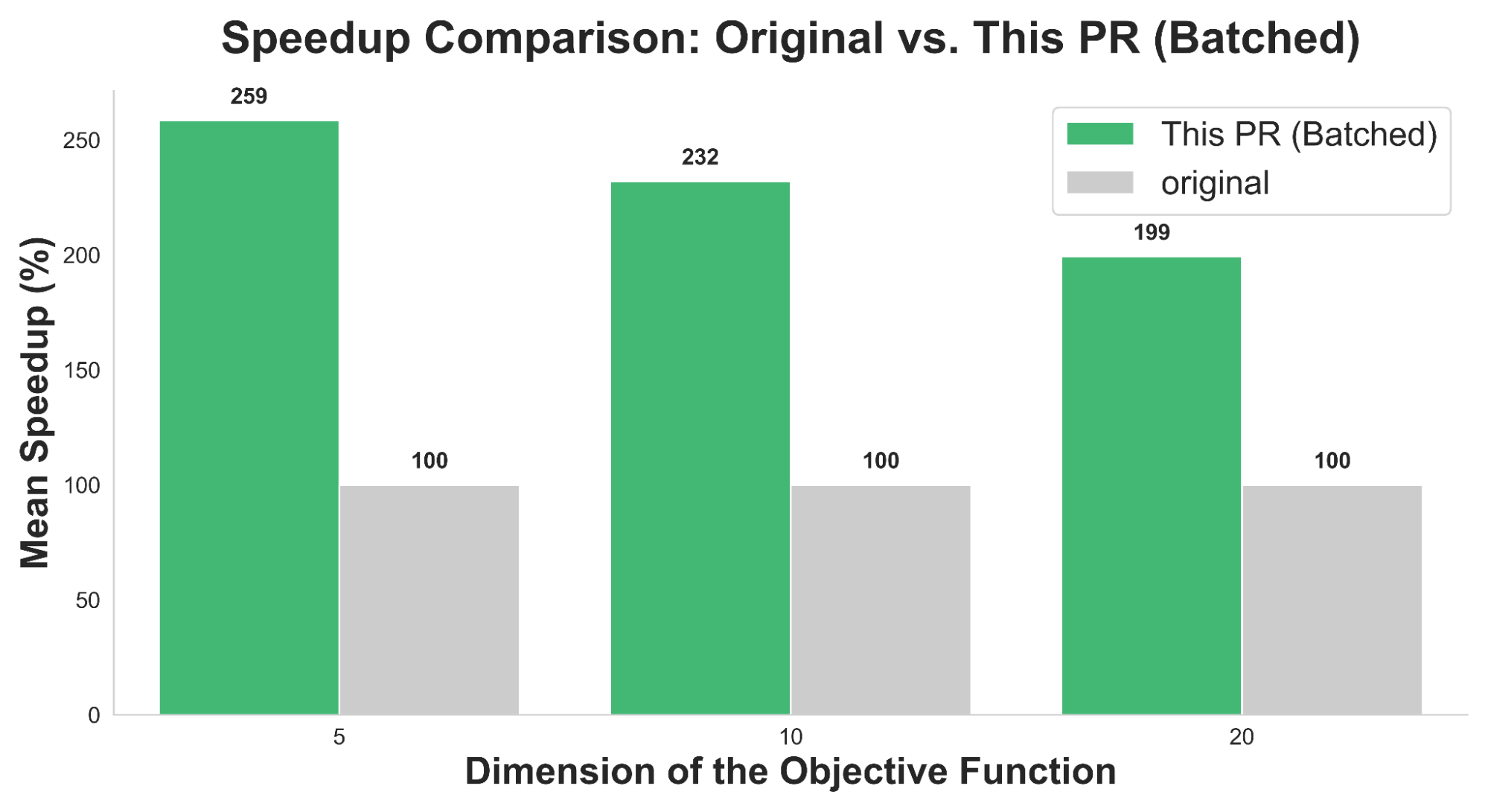
図1. 本インターンシップの成果 (#6268) による高速化効果を目的関数の次元ごとに比較した図。横軸は目的関数の入力の次元 (5, 10, 20) を、縦軸は 300 Trials 後に元のOptuna実装に対して何倍高速化したかを表します。例えばMean Speedupが200%の場合、元の実装よりも平均実行時間が1/2になったことを表します。各次元に対する実行時間は、OptunaHub の BBOB ベンチマークから計5つの関数 (f1, f6, f10, f15, f20) を選び、3つのシード値を用いて計算した場合の実行時間の平均値をとっています。

本インターンシップの成果を含む最新のGPSampler を利用するためには最初に必要な依存関係をインストールする必要があります。

# Optuna v4.6.0 のリリース以降は "pip install optuna==4.6.0" で利用可能になります．
$ pip install git+https://github.com/optuna/optuna@master 
# GPSampler には scipy と torch も必要となります.
$ pip install scipy torch greenlet

依存関係のインストール後に GPSampler を以下のように利用できます。

import numpy as np
import optuna
 
def objective(trial: optuna.Trial) -> float:
    x = trial.suggest_float("x", 0.0, 2 * np.pi)
    y = trial.suggest_float("y", 0.0, 2 * np.pi)
    return float(np.sin(x) + y)
 
sampler = optuna.samplers.GPSampler()
study = optuna.create_study(sampler=sampler)
study.optimize(objective, n_trials=100)

今回の成果により、高速化されたGPSamplerを体感して頂ければ幸いです。

はじめに

Optuna はブラックボックス最適化フレームワークの OSS で、ブラックボックス最適化は材料探索や工業製品のデザイン最適化など幅広い分野で利用されています。ブラックボックス最適化では、パラメータの提案と評価 (提案＋評価をTrial、評価される関数を目的関数と呼ぶ) を繰り返します。例えば、デザイン最適化では、Optuna によるデザインの提案と、ユーザによるデザインの評価とを繰り返すことでデザインを最適化します。特にパラメータの評価自体に時間がかかる (数分〜数時間) 場合、より少ない回数のパラメータ提案で、最適値に収束することが期待されます。

Optuna にはパラメータ提案のアルゴリズム (Samplerと呼ぶ) が多く用意されており、その中でもガウス過程ベースのベイズ最適化Samplerである GPSampler は連続変数の最適化性能が高いことで知られています。その一方で、GPSampler は他の Sampler に比べて、提案に時間がかかることも知られています。そのため、問題設定によっては 500 Trials で数時間かかる場合もあります。この問題を軽減するために、本インターンでは GPSampler の高速化に取り組みました。具体的には、GPSampler には並列化可能なボトルネックがあり、その並列化を行うことで高速化します。本インターンでの貢献は、 (1) 並列化手法の調査、(2) 並列化手法の速度の検証、(3) OSS としての保守性とユーザー体験を考慮した並列化手法の実装および Optuna への Merge (#6268) です。

GPSamplerとその課題

GPSamplerは、以下の4ステップでパラメータの提案を行います。

• ステップ1. 今までの観測データ (パラメータとその目的関数値, Optunaの用語で Trials) を用いて、ガウス過程モデルを訓練
• ステップ2. ガウス過程モデルを用いて、「獲得関数」を構築
• ステップ3. 獲得関数の値を最大化するようなパラメータを提案
• ステップ4. 提案されたパラメータで目的関数を評価して、ステップ1へ戻る

ここで、「獲得関数 (acquisition function) 」とは各パラメータの提案の優先度をモデル化した関数です。GPSampler のボトルネックの一つは上記のステップ3であり、この処理は並列化可能であることが知られています。一方で、利用可能な並列化手法の候補や、各手法の高速化の効果については今まで調査されていませんでした。

獲得関数のマルチスタート最適化

まず、前項のステップ3の処理を具体的に説明します。

図2. マルチスタート最適化の概念図 (Garnell, E [1] の図5.10より引用) 。複数の初期値 (黒色の点) から最適化を行い、最良の局所最適解 (灰色の点) を選択します。

前節で述べたように、各Trialにおいて、GPSamplerは獲得関数を最大化するようなパラメータを提案します。獲得関数の最適化ルーチン (下記の optimize_acqf 関数) は、大まかに以下のような処理を行います。

# 従来の逐次的なマルチスタート最適化
def optimize_acqf(acqf, starting_points):
    local_solutions = []
    for x0 in starting_points:
        # 各初期値x0から、一つずつ局所最適解を計算する
        local_solution = scipy_optimize(acqf, x0)
        local_solutions.append(local_solutions)
    # 得られた局所最適解の中から最良のものを選択
    best_solution = find_best(local_solutions)
    return best_solution

上記の scipy_optimize 関数は局所最適化を行います。つまり、最適化したい関数と初期値を受け取って、1つの局所最適解 (上記の local_solution) を返します。図2のように、複数の初期値 (上記の starting_points) から局所最適化を行い、複数の局所最適解を求め、その中で最善の解を選択する手法をマルチスタート最適化と呼びます。得られる解 (上記の best_solution) が大域的最適解である保証はありませんが、局所最適解を複数列挙することで、解の精度を高めることができます。

上記コードの4-7行目にあるように、Optuna v4.5までは異なる初期値10点を用いた局所最適化を逐次的に実行しています。各局所最適化は独立しており、この逐次処理を並列化することで高速化が期待されます。

並列化手法とその調査の結果

マルチスタート最適化の並列化により、高速化は期待できるものの、その包括的な調査および速度検証は行われていません。本インターンシップでは、GPSampler 高速化に向けて、(1) 利用可能な並列化手法の候補、(2) 各手法の高速化性能と精度への影響、そして (3) Optunaに組み込むための具体的な実装方法について、調査・検証しました。

調査の結果、大きく分けると「マルチプロセッシング」、「Stacking」、「Batched Evaluation」の3つの手法がありました。詳細は次節に任せますが、マルチプロセッシングは複数プロセスでの並列化、Stackingは、ベイズ最適化の OSSライブラリである BoTorch で採用されている方法、Batched Evaluation は獲得関数の評価のみを並列化する方法を指します。なお、Stacking や Batched Evaluationという名称は一般的なものではなく、本稿でのみ用いている名称であることに注意してください。また、テンソル演算のバッチ化も、内部ではスレッド並列が行われていることから、広義の並列化とみなして議論します。

マルチプロセッシング

マルチプロセッシングは、各局所最適化を独立したプロセスで並列実行する単純なアプローチです。マルチプロセッシングのメリットは実装が単純である点です。一方、デメリットはプロセスの起動とプロセス間通信のオーバーヘッドおよび、SamplerのAPIに変更を要することです。詳しく述べると、プロセス起動のオーバーヘッドを避けるため、study.optimizeを行う前にプロセスプールを起動して、Samplerに持たせるため、プロセス終了の処理が必要となり、SamplerのAPIに変更が必要になります。

Stacking

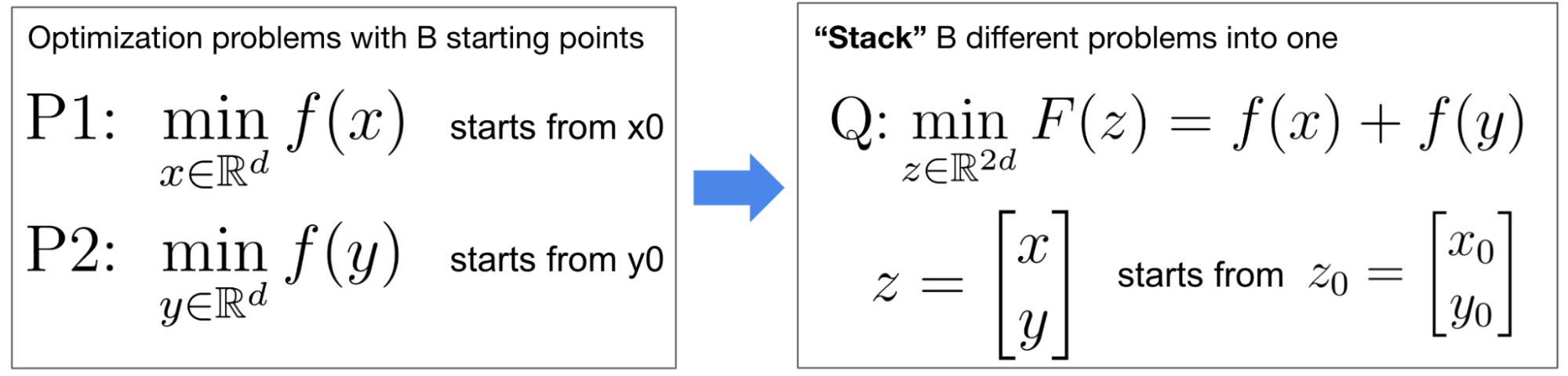
図3. B=2の場合のStackingの定式化。逐次的に2個のd次元最適化問題 P1, P2  (左図) を解く代わりに、2d次元最適化問題Qを解きます。変数 x と y は独立であることから、問題 P1, P2 と問題Qは数学的に等価です。

獲得関数の計算は、主にPyTorchによるテンソル演算で構成されます。テンソル演算は、複数のテンソルをまとめ (バッチ化し) て一つのテンソルとして処理することで、高速化を図ることができます。図3にあるように、StackingはB個の最適化問題 P1, …, PB (左図) の代わりに、各目的関数の和を新たな目的関数とする最適化問題Q (右図) を解くという手法です。これは執筆時点 (2025年9月下旬) で BoTorch に利用されている方式です。問題Qでは、B点の獲得関数評価のテンソル演算のバッチ化が可能であるため、Bが極端に大きくない限りは高速化が期待されると記述されています。詳細に関してはこの記事をご覧ください。

Stacking のメリットは実装が単純である点です。一方、デメリットは獲得関数最適化精度が劣化してしまう点であり、これが機能導入における課題となりました。より正確に言うと、GPSampler で利用されている準Newton法の一種である L-BFGS-B と Stacking を組み合わせると最適化精度が劣化します。詳細については付録を参照してください。

Batched Evaluation

Batched Evaluationは、最適化の一部の処理のみ切り出してバッチ化する手法です。最適化問題としては図3 (左図) を解きつつ、獲得関数の評価のみバッチ化する方法であるため、マルチプロセッシングとStackingの中間的な手法です。実際の処理を例に具体的に説明します。GPSamplerで用いられる局所最適化のアルゴリズム (準Newton法) では、次の2ステップを繰り返します。

• ステップ1. 現在の点xに対する関数値と勾配を評価
• ステップ2. ステップ1で得た関数値と勾配を用いて x を更新し、ステップ1に戻る。

獲得関数の最適化では、ステップ1でPyTorchによる重いテンソル演算を呼ぶため、ステップ2の処理はステップ1と比べてほぼ無視できるほど高速です。そのため、ステップ1をまとめて処理 (バッチ化) し、ステップ2の部分は逐次的に計算するというのがBatched Evaluationのアイデアです。

Batched Evaluationのメリットは、解の更新ロジックは逐次的に実行した場合と変わらないため、最適化性能が劣化しない点です。一方、SciPyのインターフェースとの統合が難しい等の実装上の課題があります。この解決が実装の肝であるため、詳細は「マージのための課題と解決策」の節で説明します。

速度の検証結果

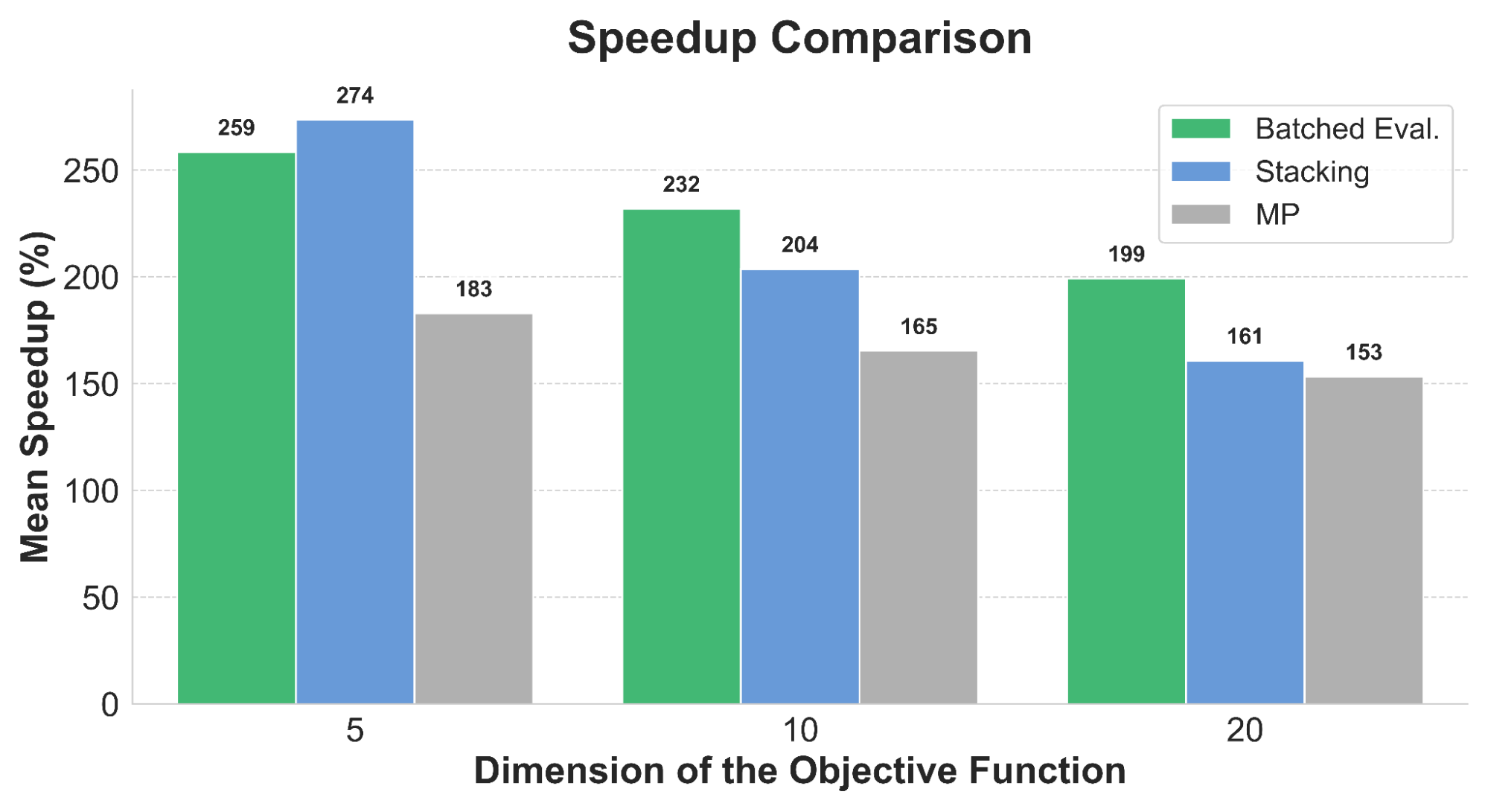
図4. 各並列化手法の 300 Trials 目における高速化効果を目的関数の次元ごとに比較した図。MPはマルチプロセッシングを表します。詳細は図1の説明を参照してください。図1と異なり、Stackingとマルチプロセッシングの高速化効果も示しています。

次に、それぞれの高速化の手法の速度を検証しました。ベンチマークの結果は図4の通りです。この結果から、高速化によって実行速度がおよそ1.5〜2.5倍高速化されたことがわかります。特にBatched Evaluationは目的関数の高次元であっても高速であることがわかります。

それぞれの並列化手法のメリット・デメリット

表1. 各並列化手法のメリット・デメリットの比較表。MPはマルチプロセッシングを表します。

それぞれの手法のメリット・デメリットをまとめると表1のようになります。これらの比較検討の結果、高速化性能が最も高く、かつ最適化精度も劣化しないBatched Evaluationを採用しました。Stacking は最適化の速度および精度、マルチプロセッシングは限定的な速度向上およびAPI変更が必要となることが問題となり、採用を見送りました。

マージのための課題と解決策

表1にもある通り、Batched Evaluation で高速化が見込まれる一方、Optunaに組み込むにあたっては複数の技術的な課題がありました。本節では、課題と実際に行った解決策について解説します。

実装上の主な課題

Batched Evaluationの実装の主な課題は、 (1) SciPyのAPI仕様と (2) Optuna の保守性とユーザー体験への考慮に関するものです。

GPSamplerの獲得関数最適化に用いる、SciPy の最適化モジュールは、最適化の反復の途中で処理を中断・再開するAPIを公開していません。そのため、最適化中の関数評価のみをバッチ化する Batched Evaluation は、既存のAPIでは単純には実装できません。初期プロトタイピングでは、SciPy の内部モジュールに依存することによってこの制約を回避した上で Batched Evaluation を実装しました。一方で、SciPy の内部モジュールは APIの安定性が保証されていないことから、将来のバージョンアップで動作しなくなる可能性があり、 GPSampler の安定性が損われる可能性があります。この問題を解決するような別のライブラリを利用することも一案ですが、依存関係の追加によって GPSampler を利用できなくなる環境を増やしてしまう可能性が発生します。これらを鑑みると、「新たな外部ライブラリへの依存回避」と「外部ライブラリの内部APIへの依存回避」の2点を意識する必要があります。

これらに加え、以下のような設計上の論点もありました。

• 責務の分離: バッチ化という機能の責任は、どのモジュールが持たせるべきか。GPSampler 自身か、最適化アルゴリズムか、獲得関数か。

• 実装の範囲: どの範囲の処理をバッチ化するか。連続最適化のみか、連続最適化・離散最適化の両方か、他のルーチンまで範囲を広げるか。

解決策: コルーチンライブラリ Greenlet を用いた Batched Evaluation

最終的には、コルーチンライブラリである Greenlet を用いて Batched Evaluation を実装することで、master ブランチにマージ (#6268) することができました。Greenlet は軽量なコルーチンを提供する OSS で、すでに Optuna の依存先ライブラリでも利用されています。この実装により、既存 API の変更や精度の劣化および外部ライブラリの内部実装への依存なしに、GPSampler を2.0〜2.5倍高速化することができました。

次に、Greenlet による Batched Evaluation について詳しく説明します。

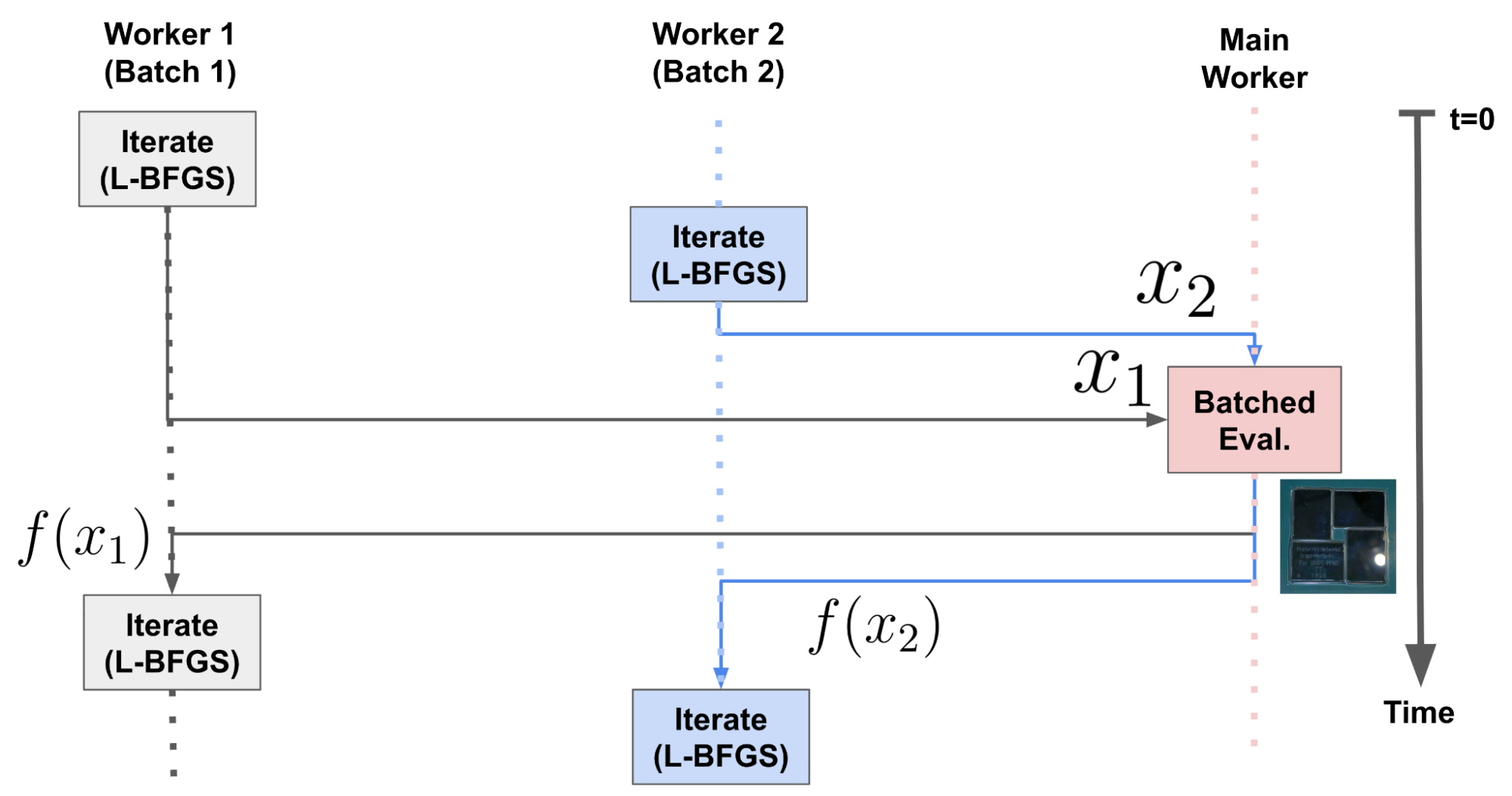
図5. コルーチンを用いた Batched Evaluation の処理の流れ。

Batched Evaluation は、1つのメインワーカーと、各初期値に対応する複数のワーカーによる協調動作で実現できます。言い換えると、実際の計算は並列に行わず、各時刻でどれか1つのワーカーのみが動作しますが、処理を効率的に遅延・切り替えすることで、重い処理のバッチ化を可能にします。具体的には、以下のような手順を行います。

• ステップ1. 各ワーカーが関数値 f(x) とその勾配 ∇f(x) を評価したい点 x  (図5の x1,  x2) をメインワーカーに渡して処理を一時停止する。
• ステップ2. メインワーカーは全てのワーカーから評価したい点 x を受け取ったら、その関数値とその勾配をバッチで計算 (図5の Batched Eval.) して、各ワーカーに結果を返す (図5の f(x1), f(x2))。
• ステップ3. 各ワーカーは処理を再開し、メインワーカーから受け取った関数値を用いて、x を次の点に更新 (図5の Iterate) してステップ1に戻る。

なお、Python の multithreading でも同様の処理は実装できますが、オーバーヘッドが大きく、十分な高速化性能が得られませんでした。そこで、起動と切替が軽量かつ高速な Greenlet を採用しました。また Greenlet をインストールできない環境に対応するために、既存の逐次処理にフォールバックする機構と本機能の単体テストの追加 (#6274) まで実施しました。

設計議論の結果

最後に設計議論の結果について述べます。第一に、バッチ化機能の責務はOptimizer (最適化アルゴリズム) に持たせました。これは、代替案であった獲得関数モジュールへの実装が、連続最適化と離散最適化のロジックの密結合を招き、保守性と拡張性を低下させる懸念があったためです。第二に、実装の範囲は、高速化の必要性が高い連続最適化のみを対象としました。範囲を限定することで、実装の複雑さを抑えながらも、最も効果的な部分の高速化を実現しました。

おわりに

インターンに応募した時点では、「ブラックボックス最適化」や「ガウス過程」についてほとんど知らない状態でした。しかし、「Optuna開発、面白そう！」という純粋な好奇心で応募した結果、毎日課題と発見の連続で、夢中で開発に取り組むことができました。もしインターンのテーマを見て少しでも心が動いた方がいれば、専門知識に自信がなくてもぜひインターン応募に挑戦してみてほしいと強く思います。

前半は手法の調査やベンチマーキングが主で、研究開発に寄ったインターンでした。一方で後半は、masterマージに向けて、チームの方と議論しながら実装や設計を進めていく、ソフトウェア開発に寄ったインターンでした。Optunaはとても丁寧にメンテナンスされているOSSということもあり、マージまでのハードルはとても高かったですが、その分マージされたときはとても嬉しかったです。インターン当初は「BoTorchと同じく、Stackingを実装したらあっさり速くなるのではないか」という見立てもありました。しかし、実際に取り組んでみると様々な課題が浮かび上がり、色々な手法・実装方針がある中でメリット・デメリットを比較しながら技術選定を行う必要がありました。特に、広く使われているOSSの開発だからこその難しさを肌で感じることができたのが勉強になりました。開発において自分の専攻である数理最適化の知識も活かすことができ、インターンシップを通じて研究へのモチベーションも高まりました。

謝辞

メンターの渡邊さんの手厚いサポートによって、無事masterマージまでやりきることができて本当に良かったです。途中、何度か課題に直面しましたが、課題の数だけ実装や設計が洗練されたように感じます。

PRレビューや設計について議論してくださったAutoMLチームの皆さん、実装のアドバイスをくださった酒井さんにも感謝申し上げます。また、インターン期間中にお世話になったPFN社員およびインターン同期の皆様とも、たくさんお話する機会があり、とても良い刺激になりました。重ねて感謝申し上げます。

参考文献

[1] Garnell, E. (2020). Dielectric elastomer loudspeakers: models, experiments and optimization (Doctoral dissertation, Institut Polytechnique de Paris).

付録: Stacking における最適化精度に関する議論

図6. Stackingを用いても、最急降下法では各反復が一致することを表す図。

Stackingを用いても最急降下法やNewton法では、各反復で両者は完全に一致することが知られています。最急降下法の場合について図6に示します。一方で、Stacking に準Newton法を適用すると最適化性能が劣化します。これは準Newton法が過去の勾配情報からヘッセ行列を近似するため起こります。より正確に言うと、Stackingされた問題では相互に独立な問題に含まれる2変数による混合微分は数学的にゼロになりますが、準Newton法ではこの自明なゼロ成分が非ゼロと推定されます。結果として、最適化の精度が劣化して (あるいは、反復回数が非常に大きくなって) しまいます。OptunaやBoTorchでも準Newton法の一種であるL-BFGS-B法が用いられていて、これはStackingを採用する上で課題となります。