Blog
進撃の巨人3巻が11月に発売されるものと勘違いして本屋を探し回っていましたが、発売日は12月9日でした。徳永です。
前回は、確率的勾配降下法(SGD)について説明しました。今回はいよいよ、劣微分を用いた最適化手法に付いての説明をおこないます。
前回の復習
前回は、最大エントロピーモデルによる線形識別器の学習方法について説明し、最後に正則化について紹介しました。正則化については重要性を主張しきれていなかった気がするので、もう一度過学習と正則化について説明しておきたいと思います。
前回、間違いは少ないほうがいいよね、というような話をしましたが、間違いには2種類あります。一つは既知のデータに対する間違いの多さで、もう一つは未知のデータに対する間違いの多さです。既知のデータに対する間違いを経験損失と言い、未知のデータに対する間違いを期待損失、もしくは汎化誤差と言います。(間違いと損失はちょっと違いますので、興味のある方は調べてみてください。ここでは簡単のため同一視しています。)
例えば、迷惑メールの文面から迷惑メール度合いを学習し、明らかに迷惑メールっぽいものを新しく受け取った場合には自動で迷惑メールに分類して非表示にしてしまう、というようなことを考えましょう。この時、経験損失というのは、既に持っているメールに対してフィルタを適用した場合にどれだけ間違えるかという量で、期待損失というのはこれから受け取るメールでどれだけ間違えるか、という量にあたります。
このように例にあてはめて考えると、我々が小さくしたいのは期待損失であって、経験損失は小さくても大きくてもあまり関係ない、という事が分かります。もっとも、経験損失が大きいのに期待損失が小さいということは考えにくいので、経験損失の値も重要ではあります。
期待損失の正確な値は測りようがありません(VC次元を使って評価する方法などはあります)が、学習時に使ったデータでテストをすると、経験損失の値しかわかりません。そこで、例えばデータを学習用データとテスト用データに分割して、学習時には学習用データだけを使い、テスト時にはテスト用データで性能を評価する、といったことをやります。これを交差検定と呼びます。実用的には、5分割交差検定や10分割交差検定がよく使われます。これで期待損失のようなものが求まります。
期待損失と経験損失は、モデルの自由度が高く(=パラメーターの数が多い)データの数が少ない場合に乖離する傾向があります。また、学習のループを繰り返すうちに、経験損失は減少しているにもかかわらず、ある時点から期待損失の値が上昇する、といったこともよくあります。期待損失と経験損失が乖離している状態を過学習と呼びます。
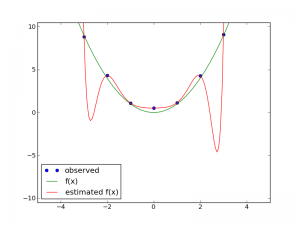
過学習の例を実際に図で見てみましょう。
緑色の線がy = x^2で、青い点がそこから少しノイズをのせた点です。観測にはノイズが必ず入るものなのでこうしてあります。赤色の線が、11次の多項式で青い観測値をフィッティングしたものです。データが7個しかないので、見事に経験損失は0になっています(赤線はすべて青い点を通っています)が、赤線と緑線の間には大きな乖離がある点が2ヶ所あり、期待損失の観点からは褒められた結果ではありません。
正則化とは、この複雑すぎるモデルに対してペナルティを与える方法です。最適化を行う目的関数に、損失項の他に正則化項を入れることによって、パラメーターの値が多くなることに対してペナルティをかけます。パラメーターが大きな値を取ろうとするとペナルティがかかるため、そのペナルティを超えて基準値をよくする(例えば、損失を少なくする)ようなパラメーターのみが大きな値を取ることができます。
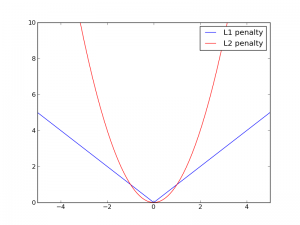
前回も説明しましたが、正則化にはいくつかの種類があり、その中でもL1正則化とL2正則化というのがよく使われています。それぞれ式で書くとL1正則化は\(r(\textbf{w}) = c \sum_i |w_i| \)となり、L2正則化は\(r(\textbf{w}) = c \sum_i |w_i|^2 \)となります。(cは正則化の効きの強さを調節するためのパラメーターで、適当に自分で決めます。0より大きな実数で、例えばc=0.01とかにします。最適な値を効率的に求める手法も研究されていますが、ここでは触れません。)\(w_i\)に対するペナルティの大きさをグラフにすると図2のような感じになります。
0に近いあたりではL1正則化(青色)の方がペナルティの値が大きくなっていることなどが見て取れます。L2正則化では\(w_i\)の値が0に近づくとペナルティの値が急速に0に近づきますが、L1正則化では0以外の点では一定の強さでペナルティがかかります。そのため、L1正則化の方が0になるパラメーターが多くなります。
長々と書いてきましたが、実は自然言語処理ではデータセットがそれなりに大きいことが多く、過学習が致命的な問題となることはあまりありません。しかし、正則化を入れるとちょっと性能が上がる事例はよくありますし、L1正則化でほとんどのパラメーターが0にできれば、パラメーターを保持するメモリ量が少なくなったり、計算が速くなったりするといったメリットがあります。このため、正則化は重要です。
劣微分とは
前回の最後で、L1正則化はパラメーターの非ゼロ要素を減らす効果が強いが、\(w_i\) = 0の位置で微分不可能なのでSGDではそもそも計算できない、という話を書きました。図2にもL1正則化のペナルティ効果が青色で書いてありますが、\(w_i\) = 0の点は左側から近づけていくと微分は-1、右側から近づけていくと微分値は1となって、両者の値が違うため、\(w_i\)=0の点では微分ができない、ということがよくわかります。
でも、よく考えてみると、微分の値として-1から1の間で適当な値を取ってもいいんじゃないかな…と思いませんか? その疑問に答えてくれるのが劣微分です。
数学的にきっちりとした劣微分(subdifferential)の定義を見てみましょう。ある点関数\(f\)の\(\textbf{x}\)における劣微分とは、以下で定義される劣勾配(subgradient)の集合です。
ある点関数\(f\)の\(\textbf{x} \)における劣勾配(subgradient)を\(\textbf{g} \)と表記することにします。以下の式を満たす\(\textbf{g} \)はすべて、関数\(f\)の\(\textbf{x} \)における劣勾配です。
すべての\(\textbf{x}’ \in \mathbb{R}^n \)に対して、
\(f(\textbf{x}’) \ge f(\textbf{x}) + \textbf{g} \cdot (\textbf{x}’ – \textbf{x}) \)
劣勾配と劣微分の言葉の使い分けは、劣勾配が具体的な値で、劣微分は劣勾配の集合であるというところです。
例えば、L1正則化の正則化項の場合は、\(w_i = 0\)において微分不可能ですが、この時、\(-c \le g \le c\)が劣微分であり、この条件を満たす\(g\)はすべて劣勾配です。例えば、0は劣勾配ですし、\(-c\)以上\(c\)以下を満たすような実数であるような0.5c、-0.3cなども劣勾配です。
微分可能な点では劣微分の値は一つに定まり、その値は微分の値と一致します。
劣勾配法
劣勾配法は劣微分を使って最適化を行う手法です。SGDでは微分不可能なところは計算しようがありませんでした。劣勾配法は、微分不可能な点では劣微分の値のどれかを採用する、という手法です。これによって、微分不可能な点が含まれている場合でも、最適化が行なえます。その他の点ではSGDと変わりません。
微分不可能なところがないと劣勾配法はSGDと完全に同じになってしまうので、ここではSVMを最適化することにしましょう。天下り的に最小化するべき式を書いてしまうと、SVMでは以下の式を最小化します。
\(L(\textbf{w}) = \sum_i f(\textbf{w}, \textbf{x}_i, y) + r(\textbf{w})\)
ただし、fは\(\max(1 – y \textbf{w} \cdot \textbf{x}, 0)\)となります。これをHinge lossと言います。また、\(r(\textbf{w})\)はSGDの場合と同じく正則化項です。ここではL1正則化を採用することにして、\(r(\textbf{w}) = \sum_w c|w| \)としましょう。cは今回は0.01にでもしておきましょう。
劣勾配法では、SGDと同じく、fとrのそれぞれを\(\textbf{w}\)で劣微分したものに、適当な学習率をかけて\(\textbf{w}\)に足しあわせていきます。しつこいようですが、微分可能な点では劣勾配は勾配と同じですから、微分不可能な点で、劣勾配を使うというところがSGDと劣勾配法の違いです。
\(f\)を微分すると、\(1 > y \textbf{w} \cdot \textbf{x} \)の場合は \(y \textbf{x}\) が勾配になり、\(1 < y \textbf{w} \cdot \textbf{x} [/latex]では勾配は[latex]\textbf{0}[/latex]になります。[latex]1 = y \textbf{w} \cdot \textbf{x} [/latex]の場合は劣勾配になるので自由度がありますが、どんな値がいいのかはよくわからないので、とりあえず[latex]\textbf{0}[/latex]にしておきましょう。もちろん、[latex]\textbf{0}[/latex]が劣勾配の条件を満たしていることは確認しておく必要があります。 次に、[latex]r(\textbf{w})[/latex]を微分してみましょう。[latex]w_i[/latex]で偏微分した時、その値は [latex]w_i > 0 \)ならば1、\(\)w_i < 0 [/latex]ならば-1となります。[latex]w_i = 0 [/latex]の時が劣微分になり自由度があるわけですが、ここではその時の値を0としておきましょう。 [latex]r(\textbf{w})[/latex]は全体に対する正則化なので、データ数を[latex]n[/latex]としたとき、一つあたりの正則化項は[latex]r(\textbf{w}) / n [/latex] になります。そのため、SGDの更新式では、実際には正則化項の影響はn/c * sign(w_i)となります。 ぐちゃぐちゃ式で書くよりも、実際にコードで示したほうが理解が早いかもしれません。Pythonっぽい擬似コードで書いてみることにします。 [sourcecode language="python"] def learn_svm(x) diff = [] # 損失による勾配 if w.inner_prod(x) < 1 diff = x * y # 正則化による勾配 i = 0 while i < w.length w_i = w[i] if w_i > 0 diff[i] -= c # cは適当な定数とする elif w_i < 0 diff[i] += c w += eta * diff [/sourcecode] learn_svmは引数として一つのデータ(x)を受け取り、それがうまく分類できなかった場合には、勾配を計算してパラメーターを更新します。ただし、x, wは同じ次元の配列であり、配列同士の和や内積、スカラ積が定義されているものとします。
次回予告
劣勾配法は、SGDとほとんど同じ感じで使えて、しかも適用範囲が広いという点で優れた手法であると言えますが、L1正則化の場合、求まった解の品質があまりよくない、という問題があります。L1正則化を使うと、最適解では多くのパラメーターが0になるはずなのですが、劣勾配法ではほとんどのパラメーターが0にならないのです。実際に計算をしてみると明らかですが、0のところでパラメーターを固定するような処理は何もないので、多くのパラメーターが0に近い値を取りはしますが、0にはなりません。これでは有効なパラメーター数が減るというL1正則化のうまみが得られません。
そこで、劣勾配法のこの欠点を克服した方法として、FOBOSやTruncated Gradientがあります。次回はいよいよこれらの手法について解説します。たぶん次回が最終回です。乞う御期待!