Blog
本記事は、2019年夏のインターンシップに参加された太田真人さんによる寄稿です。
こんにちは、2019年夏のインターン生だった関西学院大学大学院M1の太田です。大学では、ベイズモデリングの応用で研究しています。インターンでおこなった業務について紹介します。
概要
私は、時系列予測に取り組みました。実問題では、データを細かい時間スケールで長期間保存できず、過去のデータから秒を分スケールに集約して保存することがあります。
他にも、数年前までは、1ヶ月や1日単位で来場者数(売り上げ)をカウントしていましたが、最近は、高い時間分解能(日にち、時間単位)で予測したい需要が高まり、細かくデータを取り始めることもあると考えます。
その場合、データを集めたばかりの頃は、時系列長が短く予測が難しいことがあります。そこで、集約されていない時系列データは直近の短い期間しかないが、集約された時系列データは長期間あるという問題設定を考え、本研究に取り組みました。毎分計測されるデータを例に出すと、集約されていない時系列データとは1分単位のデータ1つ1つを、集約された時系列データとは1時間ごとの合計等を表します。
ここで、本研究で扱う時系列データを図1に示します。青色が観測値で白色は未観測値になります。タスクは、これらの時系列データが与えられたもとで、集約されていない時系列の予測になります。
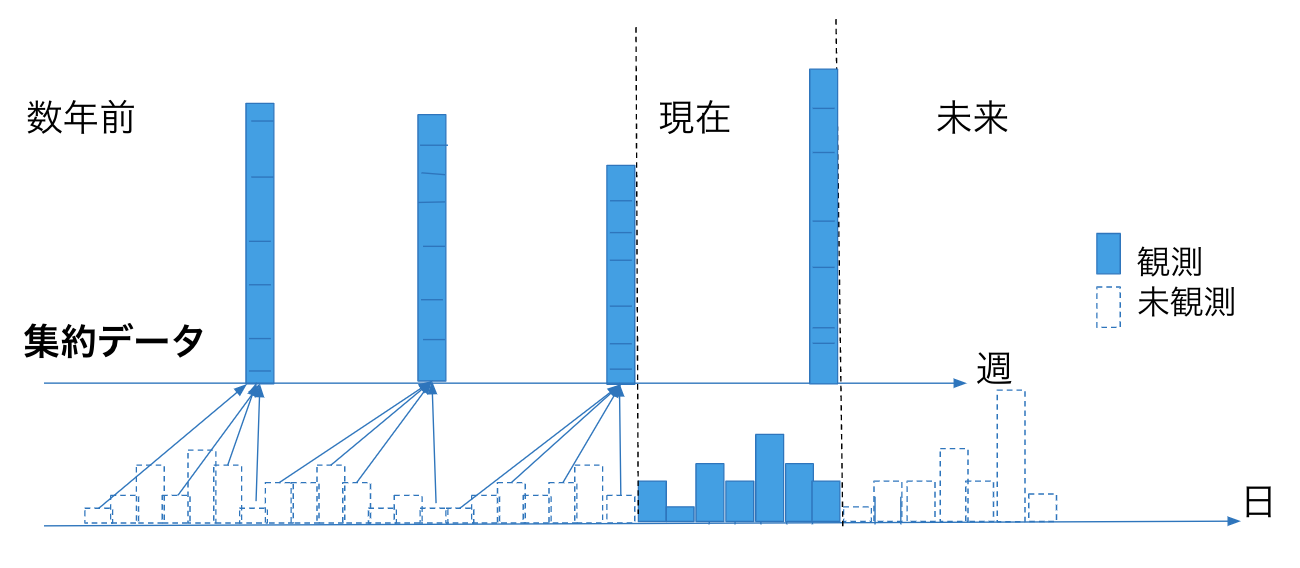
図1. 本研究で扱う時系列データ
提案アプローチにより、直近の短期間の時系列データから、高い精度で予測ができるような手法を検討しました。つまり、集約されていないデータが貯まるまで数年や数十ヶ月待つ必要が無く、なるべく早い段階で予測が行えるようになります。
アプローチ
素朴なアプローチとしては、短期間の時系列データだけで予測モデルを作ることですが、トレンドが捉えられず、予測が難しいです。
そこで、時間方向に集約された時系列データを分解(Disaggregation)することが考えられます。その素朴なアプローチは、直近の集約されていない時系列データから分解の割合の平均を計算して、過去の集約された時系列データに適応することです。
これは直近の集約されていない時系列データが少ない場合、データによっては分解が不適切になることがあります。例えば、数週間分のデータから1週間で金曜日が一番売り上げが良いとわかると、このアプローチだと過去の集約されたデータを分解するときに、金曜に多く売り上げが割り振られてしまいます。本当は、夏季休暇と通常時で売り上げの量が変わるなど、違う場合は多くあると思います。1週間や2週間分のデータで過去の全てに適応するのは不適切です。
提案アプローチはこれらを解決する方法を作りました。まず、提案アプローチを図2を用いて簡単に説明すると、上段の集約された時系列データを分解しつつ、下段の分解された赤色の推定値と青色の集約されていない時系列データを合わせて、時系列モデルを学習し、未来の集約されていない時系列データを予測する確率モデルです。
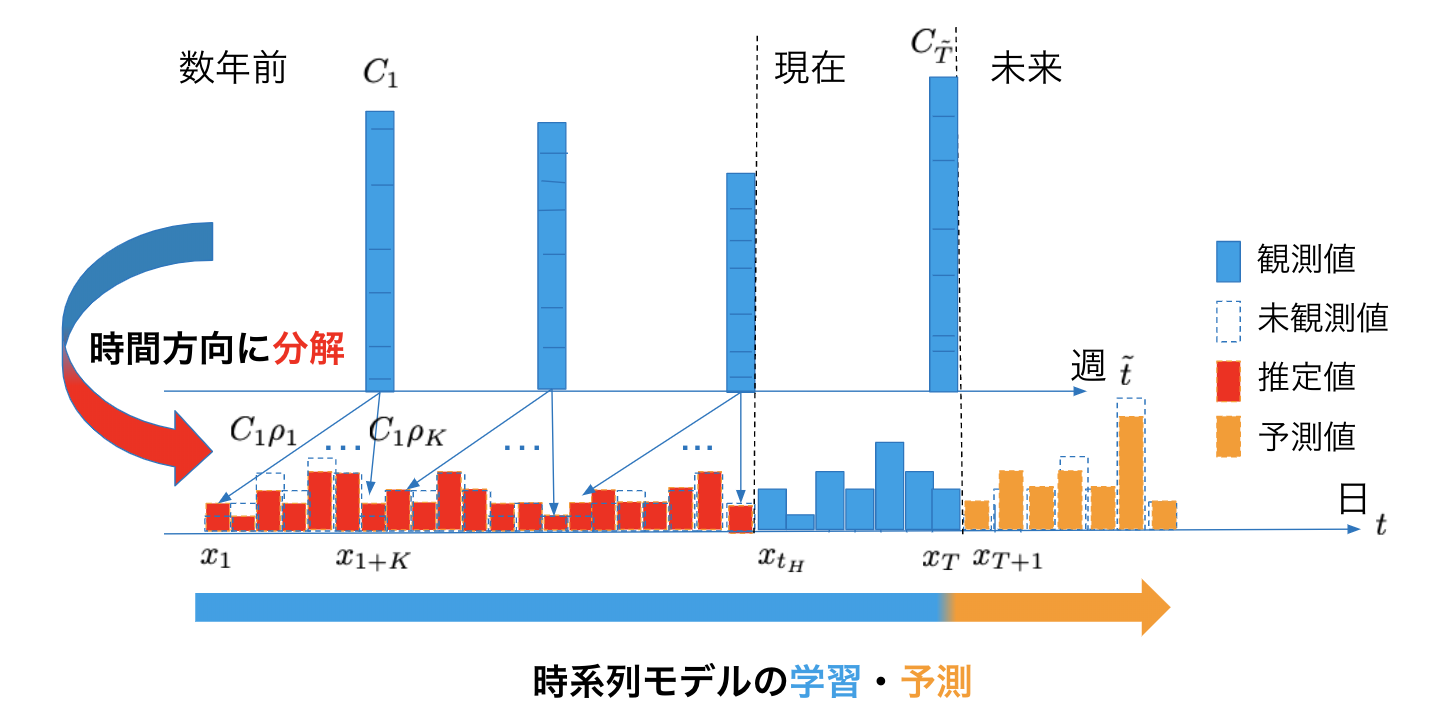
図2. 提案アプローチの概略
詳しく説明していくと、集約された時系列データは、図2の上段のように\({C}_{\tilde t}\ ({\tilde t}=1,\dots,{\tilde T})\)と集約されていない時系列データは下段のように \({x}_{t}\ (t=1,…,T)\)と表します。このとき、集約されていない時系列データは\(x_{t_H}\)まで未観測のデータになります。この集約された時系列データとされていない時系列データの関係は,時間方向の合計\(C_{\tilde t}= \frac{1}{K}\sum_{i =1}^K x_{i+({\tilde t}-1)K}\)によって求まります。ここで、集約された方の時系列長は\({\tilde T}=T/K\)と表せ、\(K\)は自分で決定するパラメータになります。例えば、1日のデータを24時間に分解したければ、\(K=24\)になります。
集約された時系列データの分解比率は, \({\rho} = {\rho}_1,…,{\rho}_K\)とあらわし、この分解比率は時間に依存しない確率変数として扱い、ディリクレ分布 \({\mathrm Dir}({\alpha})\)に従うと仮定します。ディリクレ分布を用いることで、分解した後のデータの総和がまた集約されたデータに戻ることを保証します。
尤度関数は \(\prod_{t}{\mathcal N}({x}_t|f_{\theta}( {x}_{<t}),{\sigma}^2)\)とします。 \(f_{\theta}( {x}_{<t})\) は,時系列モデルであり,本研究では,AR(Auto Regressive)モデルとFacebookが開発したProphet[1]を使用しました。\({\theta}\)は時系列モデルのパラメータになります。
同時分布は、\(p(x_{\le T},{\mathbf \rho}|C_{\le \tilde{T}}) = p(x_{\le T}|{\mathbf \rho}, C_{\le \tilde {T}}) p_{\alpha}({\mathbf \rho})\)となります。ここで、\(p_{\alpha}({\mathbf \rho})\)のディリクレ分布のパラメータは、完全に一様分布にするのではなく、直近の集約されていない時系列データから求まる分解比率をほどよく生成するような値にします。(一様分布にすると、分解比率の事前の信念として、全て均等に分解されることを表します。)
では、そのようなパラメータ値を求めるために、次の同時分布\(p(x_{t_H:T},{\mathbf \rho}|C_{{\tilde t_{H}}:{\tilde T}})=p(x_{t_H:T},{\mathbf \rho}|C_{{\tilde t_{H}}:{\tilde T}})p({\mathbf \rho})\)について説明します。この分布は、直近の集約されていない時系列データと分解比率の同時分布です。尤度関数にあたる\(p(x_{t_H:T},{\mathbf \rho}|C_{{\tilde t_{H}}:{\tilde T}})\)は、\(\prod_{{\tilde t}={\tilde t}_H}^{\tilde T}{\mathcal N}({\mathbf x}_{\tilde t}|C_{\tilde t}{\mathbf \rho},\sigma^2)\)と表します。ここで、\({\mathbf x}_{\tilde t}=(x_t,…,x_{t+K})^{\rm T}\)となります。また、\({\tilde t_{H}}\)は、集約されていない時系列データが観測され始めた時の集約された時系列データでの時刻です。
事前分布\(p({\mathbf \rho})\)は、ディリクレ分布です。ただし、ここでは、\({\mathbf \alpha}=1\)として、一様分布にしました。この同時分布から事後分布\(p({\mathbf \rho}|x_{t_H:T},C_{{\tilde t_{H}}:{\tilde T}})\)を、変分推論により求めます。近似事後分布には、ディリクレ分布を仮定します。この近似事後分布は、先ほど事前分布に求めていた「直近の集約されていない時系列データから求まる分解比率をほどよく生成する」ことを実現しています。したがって、近似事後分布の変分パラメータ\({\tilde \alpha}\)を先ほどの事前分布\(p_{\alpha}({\mathbf \rho})\)のパラメータとして用います。つまり、事後分布を事前分布として用いることになります。
また、グラフィカルモデルは図のようになります。
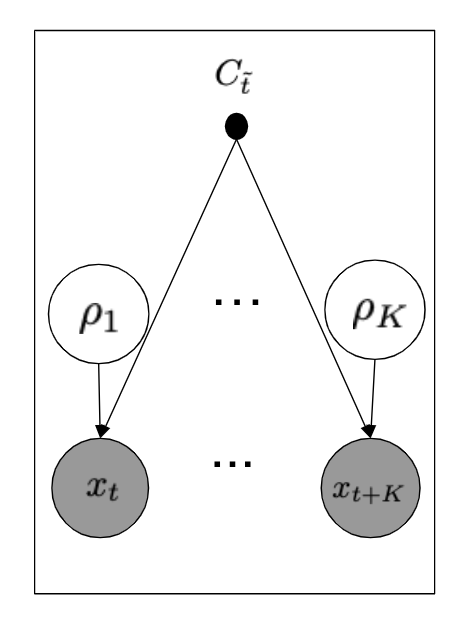
図3a. 直近の観測している集約されていない時系列データから事前分布を学習するグラフィカルモデル。
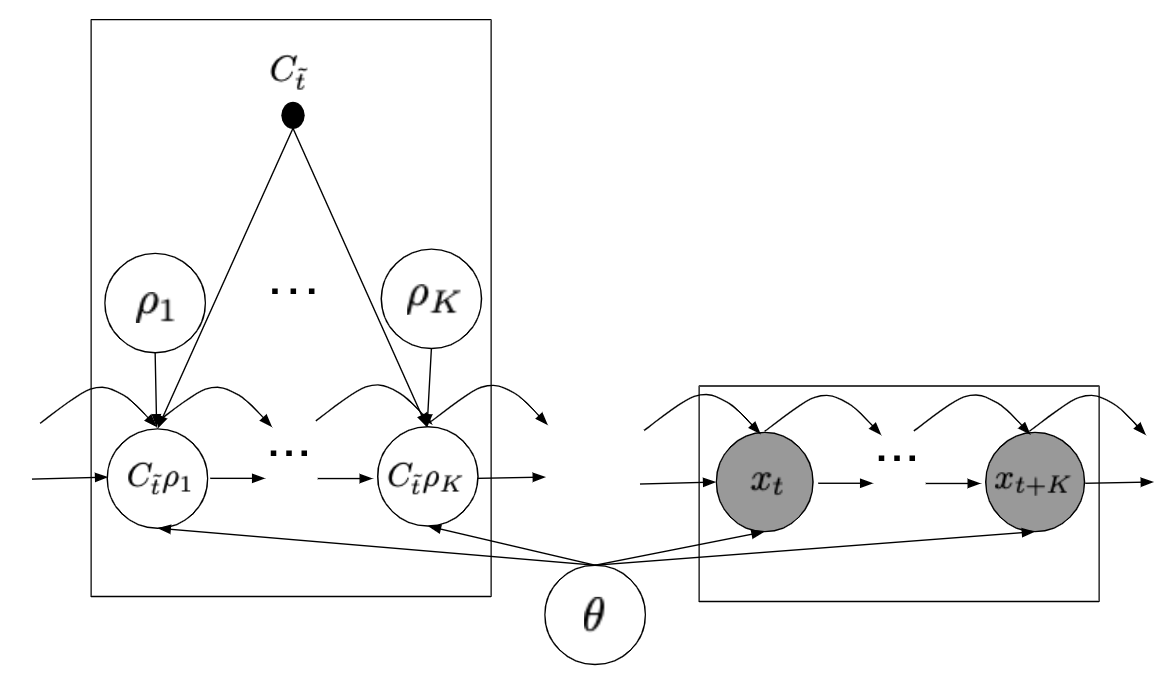
図3b. 時系列予測のグラフィカルモデル。図の左側のプレートが集約されていない時系列データが未観測時刻のグラフィカルモデルを表し、右側のプレートが観測され始めた時刻のそれを表します。θは、ARモデルのときパラメータであり、Prophetのとき確率変数になります。
この後は、時系列モデルのパラメータの学習と近似推論について説明していきます。
モデルパラメータの学習は、周辺尤度の最大化をおこないます。これは、2つのELBO(Evidence Lower BOund)の最大化により達成されます。1つ目は、
$$\log p({\bf x}_{t_H:T}|C_{{\tilde t_{H}}:{\tilde T}}) \ge \mathbb{E}_{q_{\tilde \alpha}({ \rho})}[ \sum_{t=t_H}^T \log p_{\theta}( {\bf x}_t | {\mathbf \rho}, C_{\tilde t}) ]-KL(q_{\tilde \alpha}({\mathbf \rho})|p({\mathbf \rho})).$$
このELBO最大化により、近似事後分布\(q_{\tilde \alpha}({\mathbf \rho})\)を学習します。
このELBOの1項目は、集約されていない時系列データから、分解の比率\({\rho}\)が尤もらしい値をサンプルするように\({\tilde \alpha}\)を学習する再構成誤差項です。
2項目のKL項が、\({\tilde \alpha}\)が過剰適合しないようにする正則化の役割を果たします。近似事後分布は、ディリクレ分布を仮定しており、\(p({\rho})\)のディリクレ分布(一様分布)に近づくよう変分パラメータ\({\tilde \alpha}\)を学習します。この正則化によって、素朴なアプローチのような過去のデータに対して分解を強く仮定しないため、分解時の規則性がはっきりしないノイズのあるデータに対しても予測がうまくいく可能性があります。ちなみにディリクレ分布のreparameterization trick はFigurnovら[2]が提案しています。
求めた近似事後分布\(q_{\tilde \alpha}({\mathbf \rho})\)を事前分布\(p_{\tilde \alpha}({\mathbf \rho})\)として用いて,次のELBOを最大化します。
$$\log p({\bf x}_{ \le T}|C_{\le {\tilde T}}) \ge \mathbb{E}_{q_{\alpha}({\mathbf \rho})}[\sum_{t=1}^T \log p_{\theta}({\bf x}_t|{\bf x}_{<t},{\mathbf \rho},C_{\le {\tilde T}})]-KL(q_{\alpha}({\mathbf \rho})|p_{\tilde \alpha}({\mathbf \rho})).$$
このELBOは、時系列モデルの出力を平均とするガウス分布を尤度関数に、事前確率は先ほど求めた近似事後分布をもとに、近似事後分布\(q_{\alpha}({\mathbf \rho})\)を求めながら、時系列モデルのパラメータを学習する段階になります。ARを時系列モデルに使う場合、ARモデルのパラメータは、VAE(Variational AutoEncoder)[3]のdecorderの学習方法に習い、近似事後分布を求めるELBO最大化と同時に学習します。また、Prophetを時系列モデルに用いる場合は、別途モデルパラメータの事前確率を用い、また近似事後分布を仮定し、KL項がさらに増えます。
予測分布は、以下の式で与えられます。
$$p(x_{T+1}|x_{\le T},C_{\le {\tilde T}})=\int p_{\theta}(x_{T+1}|x_{\le T, },{\mathbf \rho},C_{\le {\tilde T}})q_{{\alpha}}(\mathbf \rho){\rm d}{\mathbf \rho}.$$
ここまでを数式を使わずに説明すると、直近の時間方向に集約されているデータの分解比率を、事前分布に組み込み、過去の集約されたデータから集約されていないデータを推定しつつ、時系列モデルを学習しようというアプローチです。
以後、提案アプローチの時系列モデルにARモデルを用いた場合、TDAR (Temporal Disaggregation AR)と呼び、Prophetを用いた場合、TDProphet (Temporally Disaggregation Prophet)と呼びます。
実験
実験は、集約されていない時系列の予測精度の比較と集約さていない時系列データの量がどのくらい少なくても精度が高いのかを実験しました。データセットは、アメリカの複数地区の1時間毎の消費電力を記録したHourly Energy Consumption[4]、毎月の飛行機の乗客数を記録したAir passengers[5]、複数のレストランの毎日の来場者数を記録したRecruit Restaurant Visitor Forecasting[6]です。また、集約の方法は図4のように、毎時は毎日に、毎日は毎週に、毎月は四半期に集約しデータセットを作成しました。
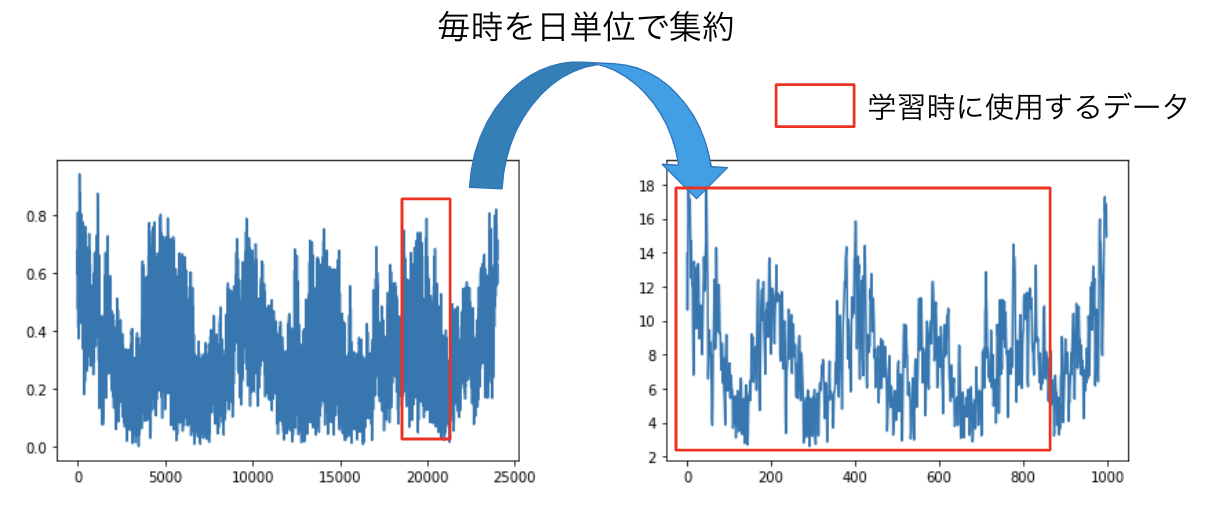
図4a. Hourly Energy Consumptionの1地区のデータを集約した時系列データ。赤枠が学習データに使用します。
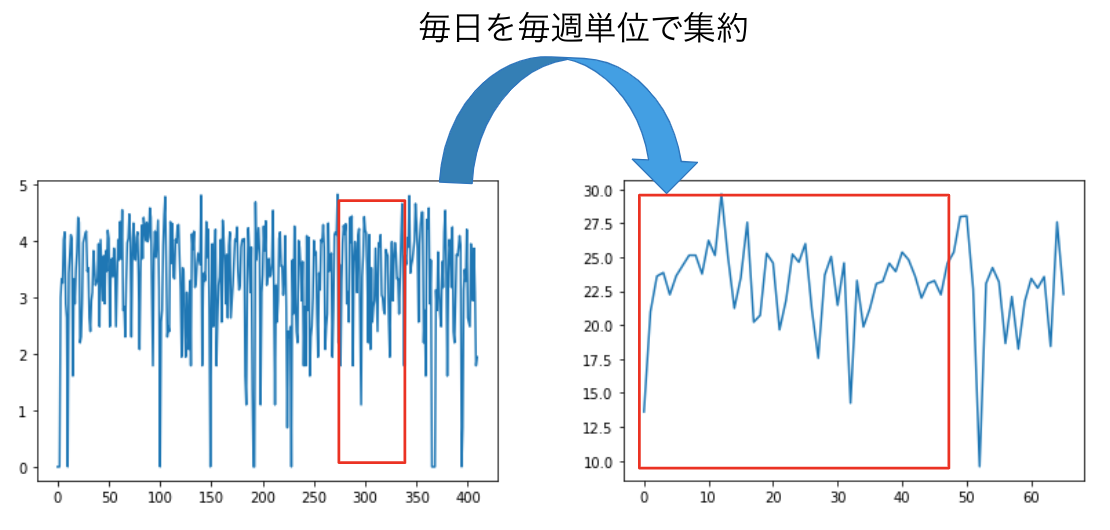
図4b. Recruit Restaurant Visitor Forecastingのデータセットの1店舗分のデータを集約した時系列データ
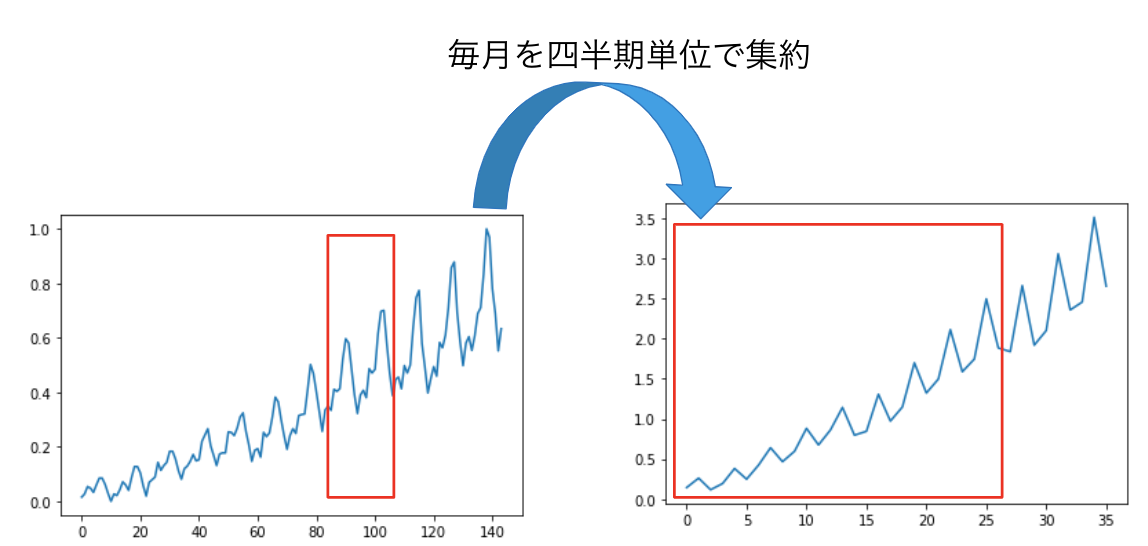
図4c. Air passengersのデータを集約した時系列データ
比較手法は、短い期間の時系列データだけで学習したARモデルと直近の集約されていない時系列データから分解比率の平均を求め、過去の集約されたデータを分解し、分解されたデータを含めて学習したARモデル(MDAR:Mean Disaggregation AR)を使用しました。また時系列モデルにProphetを使用した方は、Recruit Restaurant Visitor Forecasting (RRVF) のデータセットとAir Passengersのデータセットで試しました。
評価指標に関しては、RRVFのデータセットに対する予測にはRMLSEを用いて、他はRMSEで評価しました。予測範囲は、スケールがそれぞれ違いますが、集約されたデータ3点分の分解されたデータです。RRVFのデータなら21日分、Air passengersのデータなら9ヶ月分、Hourly Energy Consumptionデータなら72時間分になります。
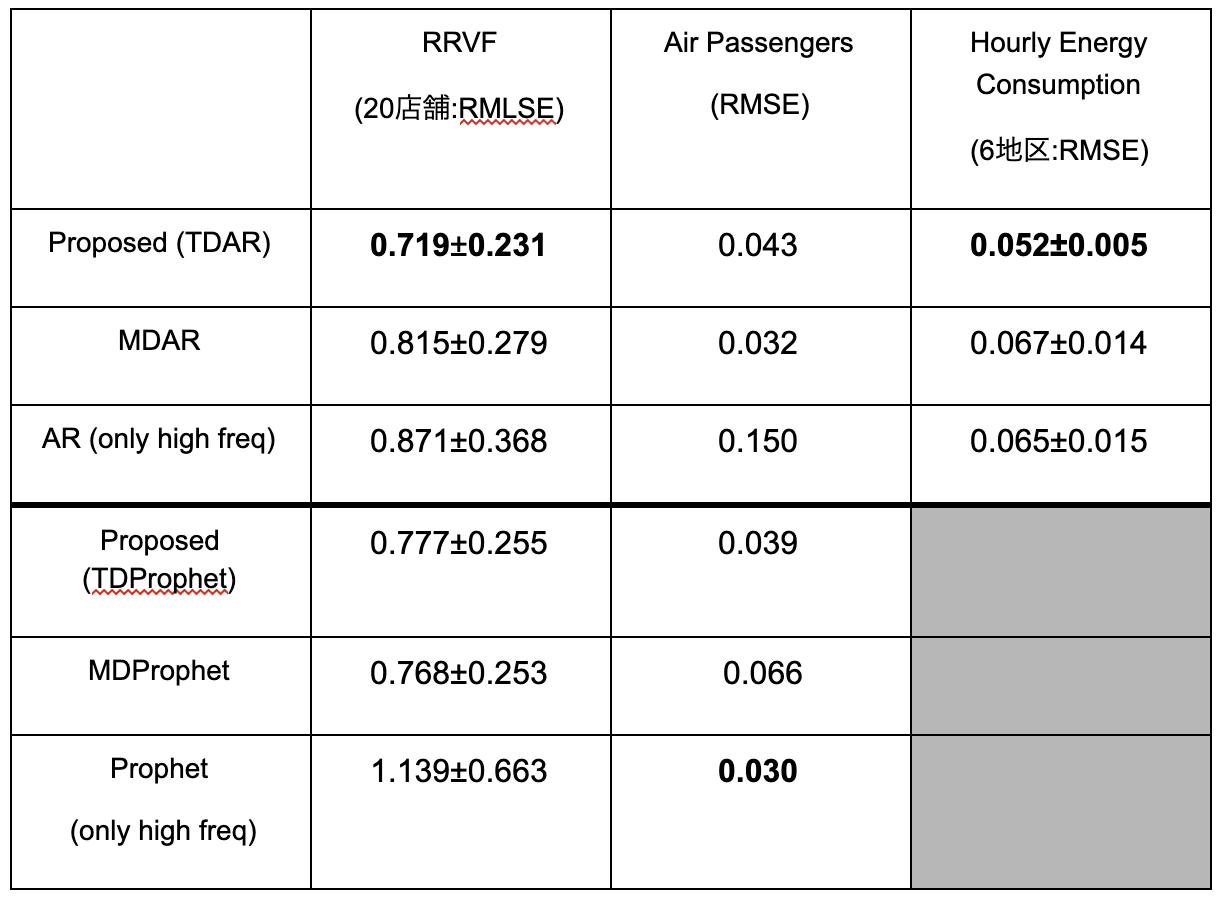
表1. 予測精度の比較
表1が実験結果になります。予測精度を比較した結果、提案手法のTDARがRRVFのデータセットとHourly Energy Consumptionのデータセットに対して精度が一番高いです。提案アプローチは、データにノイズが乗りやすく、集約されていないデータが少ない場合に効果がありました。それゆえに、Air Passengers のデータセットでは、提案アプローチはMDARに予測精度が劣りました。このデータセットは、データにノイズが少なく、直近の観測された分解比率から精度高く集約されたデータを分解できてしまうからです。また集約されたデータを活かすことにより、長期的なトレンドを捉えることができます。Air Passengers のデータセットには右上がりのトレンドがあり、直近のデータだけで学習したARモデルの場合、トレンドは捉えられないですが、集約されたデータを活かすことでトレンドは捉えることができます。
TDProphetの精度が高くないと考えられる理由は、それ以外のProphetは、MAP推定でパラメータ推定しているのに対し、提案アプローチはELBOの計算をしているため、近似事後分布のパラメータの初期値に依存し、局所解に落ちて精度が振るわなかったのかもしれません。
実験2:集約されていない時系列データの量に伴う予測精度の比較
RRVFデータセットに対して、集約されたデータは固定し、集約されていないデータがどれだけ少なくても、精度が出るのかを実験しました。図5は、横軸が集約されていないデータを2週間隔で増やし10週分、縦軸に予測精度RMLSEをとりました。
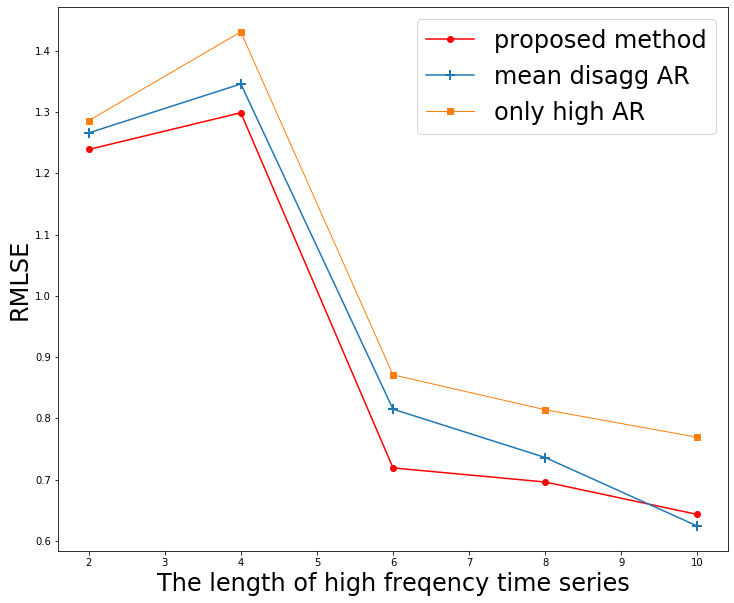
図5. 学習に使用する集約されていない時系列の長さを変えて予測精度の比較
縦軸の値が低いほど精度が高いことを示します。集約されていないデータ量が少ないときに提案手法の赤線が2か月分のデータ量が手に入る段階では、他の手法より精度が高いことがわかりました。
関連研究
本研究と一番関連のある研究は、階層時系列予測 (Hierarchical time series forecasting)[7] になります。それは、各層が異なる時間スケールで集約された時系列データを表し、一番下の層が最も細かい粒度の時系列データになります。そのデータがあたえられたもとで、どの層の予測もおこなう研究です。本研究の集約されていないデータが過去にも多く手に入っていると階層時系列予測と同じ問題設定になります。
データが少ない場合、転移学習が考えられます。時系列データの転移学習[8]は、分類や予測、分解があります。転移学習で行われている時系列分解は、多変量の時系列とそれらを集約した時系列が与えられたもとで、ある変量の時系列予測をおこなう研究です。例えば、各家の家電の消費電力とその家の合計の消費電力が複数の家が与えられたとき、ある家の家電の消費電力を予測しようという応用があります。本研究の分解は時間方向の分解なので、この転移学習で行われている時系列分解とは異なります。
最後に、時系列データではありませんが、空間的に集約されたデータの高解像度化をおこなう研究として[9]があります。この研究は、州ごとに集計されたデータを、共変量データを補助的に使用しつつ、ガウス過程を用いた確率モデルから、空間の高解像度化をしています。さらに、ガウス過程を用いながらも、100万件を超える観測データがあっても計算できるように工夫されています。
Future Work
本研究で用いた事前分布は、無情報を意味する一様分布を使用しましたが、ここにデータのドメイン知識を詰め込むことができます。例えば、長期休暇期間とそれ以外の期間でデータの分布が変わるとわかっているなら、その事前の信念を事前分布に組み込む事も考えられます。また、時系列モデルに素朴なARモデルとProphetを用いましたが、場合によってはRNNを用いることもできます。さらに、集約データの分解の比率も今回は時間に対して独立でしたが、時間方向に依存関係のあるようなモデルの拡張も考えられます。
まとめ
本研究では、集約された時系列データは長期間あり、集約されていない時系列データは直近の短期間しか手に入らない状況下で、集約されていない時系列の予測をおこなうタスクに取り組みました。アプローチとして、集約された時系列データを細かい粒度に分解しつつ時系列モデルから予測する確率モデルを構築しました。実際に集約されていないデータが少ないとき、予測精度が高いことを実験的に示しました。
最後に、インターンの中盤にこのテーマに切り替え、残りの短い時間の中で、メンターのお二人の指導があったおかげで最後までやり遂げれました。本当にありがとうございました。
参考文献
[1] Taylor, S. J., & Letham, B. (2018). Forecasting at scale. The American Statistician, 72(1), 37-45.
[2] Figurnov, M., Mohamed, S., & Mnih, A. (2018). Implicit reparameterization gradients. In Advances in Neural Information Processing Systems (pp. 441-452).
[3] Kingma, D. P., & Welling, M. (2013). Auto-encoding variational bayes. arXiv preprint arXiv:1312.6114.
[4] Hourly Energy Consumption https://www.kaggle.com/robikscube/hourly-energy-consumption
[5] Air Passengers https://www.kaggle.com/abhishekmamidi/air-passengers
[6] Recruit Restaurant Visitor Forecasting https://www.kaggle.com/c/recruit-restaurant-visitor-forecasting
[7] Hyndman, R. J., & Athanasopoulos, G. (2018). Forecasting: principles and practice. OTexts.
[8] Laptev, N., Yu, J., & Rajagopal, R. (2018). Applied time series transfer learning.
[9] Law, H. C., Sejdinovic, D., Cameron, E., Lucas, T., Flaxman, S., Battle, K., & Fukumizu, K. (2018). Variational learning on aggregate outputs with Gaussian processes. In Advances in Neural Information Processing Systems (pp. 6081-6091).




