本記事は、2019年夏のインターンシップに参加された中野裕太さんによる寄稿です。

---

皆様はじめまして。2019 年 PFN 夏季インターンシップに参加していた北海道大学の中野裕太です。本ブログでは、私が夏季インターンで取り組んだテーマである、「Graph Neural Network を用いたグラフの木幅予測」について説明します。

要旨

与えられた無向グラフがどれくらい木に近いかを表す値である木幅は、グラフ上の組み合わせ最適化問題に対するアルゴリズムの効率性や解そのものと深く関係しています。しかし、木幅を計算することは NP 困難なため、木幅を計算するには頂点数に対し指数時間かかってしまいます。そこで、今回 Graph Neural Network を用いた 2 つの方法でこの問題にアプローチしました。1 つ目は、よく知られた既存のアルゴリズムと組み合わせ探索木の枝刈りを行い高速化を図り計算する方法です。結果は、多くの場合で枝刈りがうまく働き、関数呼び出し回数が 90% 以上減少しました。2 つ目はグラフ回帰問題として直接木幅を計算する方法で、平均絶対誤差が 0.75 となりました。また、真値との誤差が 5 を超えるような、大きく間違えた例はありませんでした。

はじめに

木幅とは？

グラフ理論において木幅とは、ある無向グラフに対し定義されるグラフ不変量の一つであり、大雑把にいうとグラフがどれくらい木に近いかを表す値です。この値を厳密に定義するためにまず、グラフに対する木分解^*1というものを定義します。

ある無向グラフ \(G=(V,E)\) に対する木分解とは、下記の条件を満たす \((X = \{X_i\ |\ i \in I \},\ T = (I,\ F))\) のことをいいます。

1. \(i \in I\) に対し、\(X_i \subseteq V\) である。
2. \(V = \bigcup_{i \in I}\ X_i\)
3. 全ての \(\{v, w\} \in E\) に対し、\(v, w \in X_i\) となる \(i \in I\) が存在する。
4. 全ての \(v \in V\) に対し、\(\{i \in I\ |\ v \in X_i\}\) で誘導される、\(T\) の部分グラフが木となる。

下図に、グラフと木分解の一例を示します。

また、木分解 \((T = (I,\ F),\ X)\) に対する幅を \(\max_{i \in I} |X_i| – 1\) と定義します。例えば、先程の図における木分解の幅は 2 です。ここで、ある無向グラフ \(G=(V,E)\) に対する木幅 \(tw(G)\) は、\(G\) に対し可能な全ての木分解における幅の値の最小値として定義されます。

例えば、木に対する木幅を考えてみると、\(X_i\) を各辺の端点 2 点とすることで、定義を満たす \(T\) が構成できるため、頂点数 2 以上の木は木幅 1 を持ちます。このように、木幅が 1 に近いほどそのグラフが木に近いこと、つまり木へと分解しやすいということを意味します。また、任意の 3 頂点がサイクルを形成し、最も木から離れている完全グラフは、\(X_1\) に全ての頂点を含める以外に条件を満たす \(T\) を構成できないため、\(|V| – 1\)の木幅を持ちます。

^*1 機械学習の分野などでは Junction Tree とも呼ばれます。

木幅は何の役に立つ？

グラフ上における組み合わせ最適化問題は、大きく 2 種類に分けられます。1 つは与えられたグラフのサイズ（辺数や頂点数）に対し多項式時間で解ける問題、もう 1 つは多項式時間で解けるアルゴリズムが \(P \neq NP\) 予想の下で存在が知られていない問題です。前者の例として、最短経路問題や最大流問題、後者の例として、最大独立点集合問題や巡回セールスマン問題があります。

しかし後者の問題のほとんどにおいて、入力として与えられるグラフが木である場合に、グラフのサイズに対する多項式時間で解けるということが知られています。では、木に似ているグラフ、つまり木幅が小さいグラフではどうでしょうか？これは、先程述べた木分解を用いることで、 木幅を固定した際、つまり木幅 \(k\) が定数の場合、グラフのサイズに対し多項式時間で解けることが知られています。これは、アルゴリズム分野における Fixed Parameter Tractability (FPT) と深く関係しています。詳しくは [1] をご参照ください。

また、先程も述べたように木幅はグラフ不変量であるため、他のグラフ不変量との間で、上界や下界の関係が存在します。例えばグラフ彩色数 [2] に関して、木幅 \(k\) を持つグラフは高々 \(k + 1\) の彩色数を持つといった関係があることが知られています。詳しくは、[3] をご参照ください。

このようなことから、木幅を計算することや予測することは、グラフ上の組み合わせ最適化問題に取り組む上で重要なことといえます。

Graph Neural Network とは？

Graph Neural Network (GNN) とは、グラフ構造を扱う新しいニューラルネットワークです。一般的なニューラルネットワークでは、入力として実数ベクトルや行列、テンソルなどを扱っていますが、GNN では下記に示すフレームワークを用いるなどで、グラフ構造を扱うことを可能にしています。GNN が主に扱う問題としては、教師ありのグラフ分類・回帰問題やノード分類・回帰問題があります。GNN に関するサーベイ論文として [4] などがあります。詳細はこちらを参照してください。

GNN にも様々な種類がありますが、今回用いる大きなフレームワークとして [6] で提案されているものを用います。これは、各ノードに特徴ベクトルが与えられており、それらを一定回数更新していくことで、ノードに対する特徴表現を獲得し、グラフ全体における全てのノード特徴表現を集約することで、グラフに対する特徴表現を獲得するという仕組みになっています。

入力として、無向グラフ \(G=(V, E)\) が与えられ、各頂点 \(v \in G\) に対し特徴ベクトル \(h_v\) が割り当てられていると仮定し、具体的なノード特徴ベクトルの更新方法を下図に示します。

 

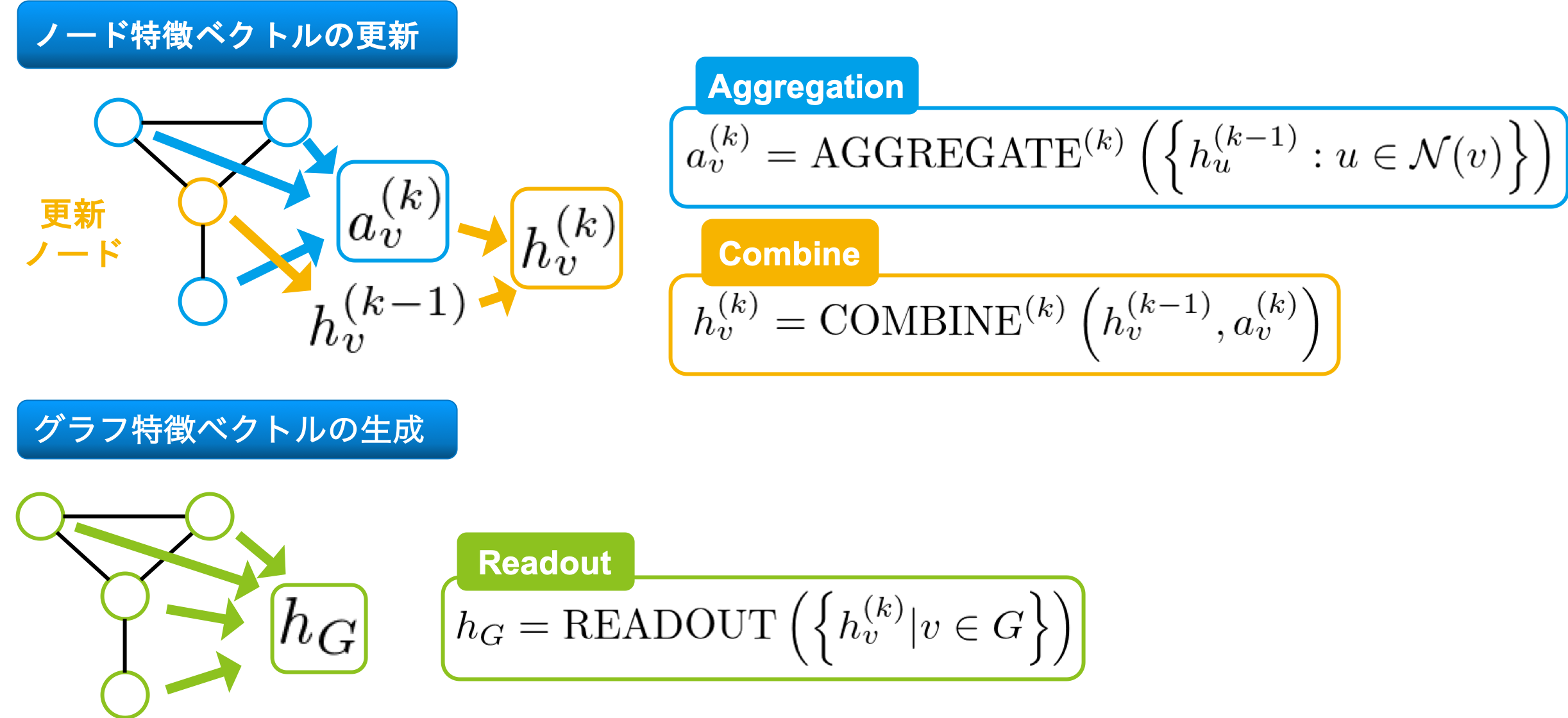
Aggregate で更新ノードの近傍（\(\mathcal{N}(v)\) で表される部分です）の特徴ベクトルを集約し、Combine で、自身の特徴ベクトルと集約した特徴ベクトルを用い、新しい特徴ベクトルを生成します。グラフ分類・回帰タスクを行う場合、最終的に Readout でグラフ全体の特徴ベクトルを生成します。

実際のモデルにおいて、Aggregation や Readout の部分にあたる特徴ベクトルの多重集合に対する関数は、Max, Average, Sum などが用いられることが多いです。例えば、Kipf らにより提案されたノード分類における GNN モデルである、 Graph Convolutional Networks (GCN) [5] では、Aggregation の部分に Element-wise mean を、Combine の部分に1層のパーセプトロンを用いています。

では、GNN の性能を最大限に引き出すためにはどのような操作が良いでしょうか？これに関し Xu らは、ノード近傍の特徴ベクトルの多重集合における区別可能性を基に考察しています [6]。これを簡単に説明します。

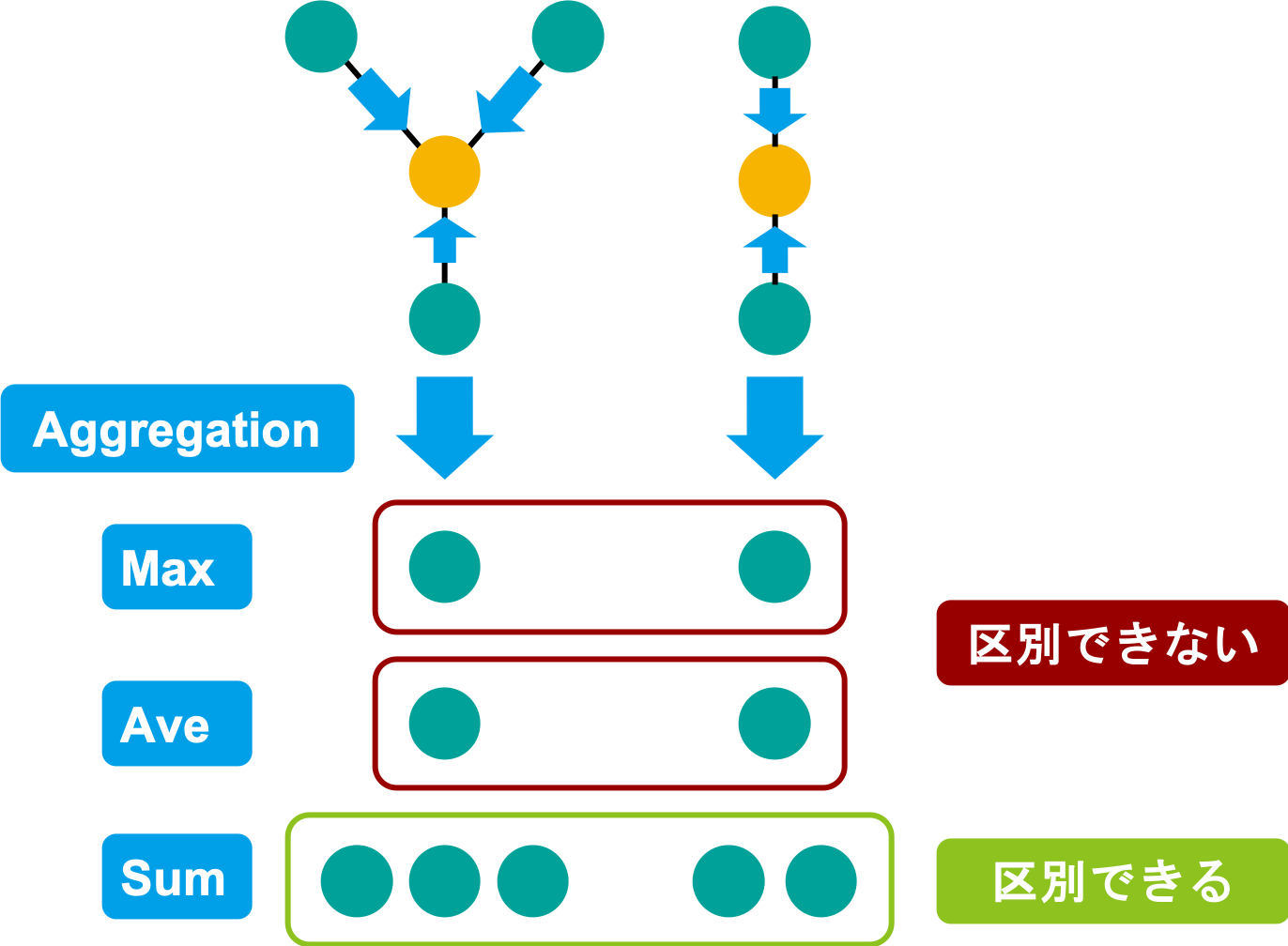
上図におけるノードの色は、特徴ベクトルを表しており、同じ色は同じ特徴ベクトルです。今、黄色のノードの特徴ベクトルを更新する際の Aggregation について、具体的な例として上げた Max と Average と Sum の 3 つについて考えます。Max や Average を取った場合は、左右どちらとも緑色が 1 つになってしまい、2 つのグラフを区別できません。しかし、Sum をとった場合、左は緑が 3 つ、右は緑が 2 つとなり、区別できるようになります。

このようないくつかの考察を通し、Xu らは Graph Isomorphism Network (GIN) と呼ばれる、Aggregation や Readout を Sum ベースに行う、シンプルなネットワーク構造を提案し、多くのグラフ分類タスクで State-of-The-Art を達成しています。今回、木幅を予測するために試したいくつかの GNN 構造は、この GIN における、Aggregation や Readout の部分を変えて得られるものを用いました。詳しくは後述するコードをご覧ください。

どのように木幅を予測するか

今回、下記に示す 2 つの手法を用い木幅の予測を行いました。

1. 既存のアルゴリズムと GNN を組み合わせての予測
2. GNN を用いた直接予測

それぞれの手法について説明する前に、今回用いたグラフデータセットについて簡単に説明します。

今回用いたグラフデータセット

GNN を学習させるためのデータセットが必要になりますが、木幅に関するデータセットはほとんどありません。見つけたデータセットとして、Parameterized Algorithms and Computational Experiments Challenge (PACE) と呼ばれる様々な組合せ最適化問題に対するアルゴリズムの設計を競うコンテストにおいて、2016 年、2017 年に木幅に関するコンテスト [7, 8] が開かれた際に用いられたデータセット [9] がありましたが、200 グラフほどしか含まれておらず、GNN の学習に用いるためには少し心許ない数量でした。そこで、ランダムにグラフを生成し、木幅を既存の木幅計算プログラムで計算することで、GNN の学習に用いるためのデータセットを作成しました。

今回、グラフを生成する際に用いたランダムグラフ生成モデルは下記の 3 つです。

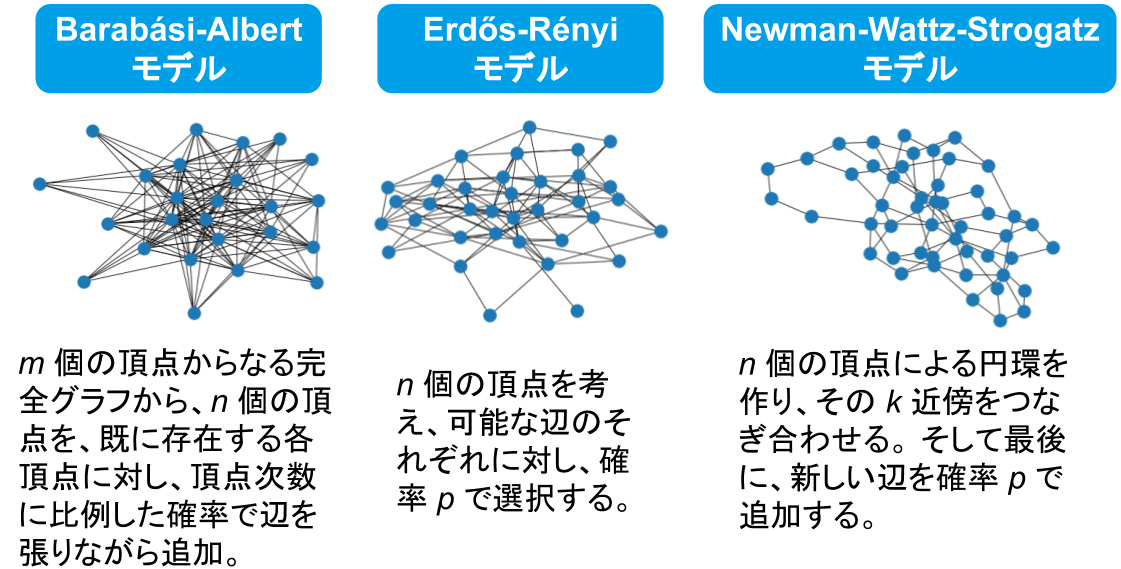
各モデルからそれぞれ 10000 グラフを生成し混ぜ合わせたデータセットを用いました。後述する各分類タスクにおいては、ラベルが均等になるように選択し、回帰タスクにおいては、30000 グラフの中から、10000 グラフをランダムに選択し、それぞれのタスクにおいてデータセットとして 1 割をテストデータ、残りを訓練データとしています。

また、ラベル付けのために木幅を計算するための既存のプログラムとして、先程も取り上げた 2017年に開催された PACE の木幅の計算コンテストにおいて提出された、明治大学の玉木先生の実装 [10] を用いました。

アプローチ 1

既存の木幅を計算するアルゴリズムに対し、GNN による木幅に関する分類タスクの予測結果を探索状態の枝刈りに用いることで、既存のアルゴリズムの高速化を図りました。

既存アルゴリズムについて

木幅を計算する既存アルゴリズムは複数あります。詳しくは [11] をご参照ください。今回は、[11] にて取り上げられていた 空間計算量、時間計算量ともに \(O^{\ast}(2^n)\)^*2 である木幅計算アルゴリズムを参考にした、下記に示す Algorithm 1 を用います。アルゴリズム中に登場する、\(\mathrm{Q}(G, S, v)\) の詳細については [11] を御覧ください。これは、あるグラフ \(G=(V, E)\) に対し \(\mathbf{TWCheck}(G, V, opt)\) を呼び出すことで、\(G\) が木幅 \(opt\) 以下であるかどうかを判定します。つまり、\(opt = 1\) から値を 1 ずつ増やしながら順に代入していき、初めて true を返した値、または \(opt = |V| – 1\) から値を 1 ずつ減らしながら順に代入していき、初めて false を返した値に 1 を加えた値として、\(G\) の木幅を計算できます。以降、前者を Lower-Calculation、後者を Upper-Calculation と呼びます。

^*2 Big-O Star 記法と呼ばれ、ある評価関数の指数部オーダのみを記述するためのものです。Parameterized Algorithm 分野でよく用いられます。詳しくは文献 [14] をご参照ください。

今回導入する枝刈り

上記の擬似コードを見ていただくとわかるように、一度の木幅判定において最大で \(\mathbf{TWCheck}\) が \(O(|V|!)\) 回呼び出されてしまいます。そこで、 \(\mathbf{TWCheck}(G, S, opt)\) が、\(G\) において、\(V\) の部分集合 \(S\) で誘導される部分グラフ \(G[S]\) の木幅が \(opt\) 以下であるかどうかを返す関数であることに着目し、この誘導部分グラフの木幅を GNN により分類し、その結果次第で枝刈りを行う部分を追加します。これにより、結果が不正確なものになる可能性と引き換えに、再帰回数が減るため関数呼び出し回数の減少、実行時間の削減が見込まれます。この枝刈りについて具体的に説明していきます。

まず、木幅がしきい値 \(thresh\) 以下かどうかでラベル付けを行った二値分類タスクの学習を行った GNN を考えます。枝刈りを行うために、 \(G[S]\) に対しこの GNN を用い推論を行います。

ここで、現在の \(opt\) の値が \(thresh\) より小さく、GNN による予測結果が \(thresh\) より大きい場合、部分グラフの木幅が十分に大きいと判断し、枝刈りを行って false を返します。これを Upper-Prune と呼びます。一方、現在の \(opt\) の値が \(thresh\) より大きく、GNN による予測結果が \(thresh\) より小さい場合には、部分グラフの木幅が十分小さいと判断し、枝刈りを行って true を返します。これを Lower-Prune と呼びます。これら 2 つの枝刈りをまとめたものを下図に示します。

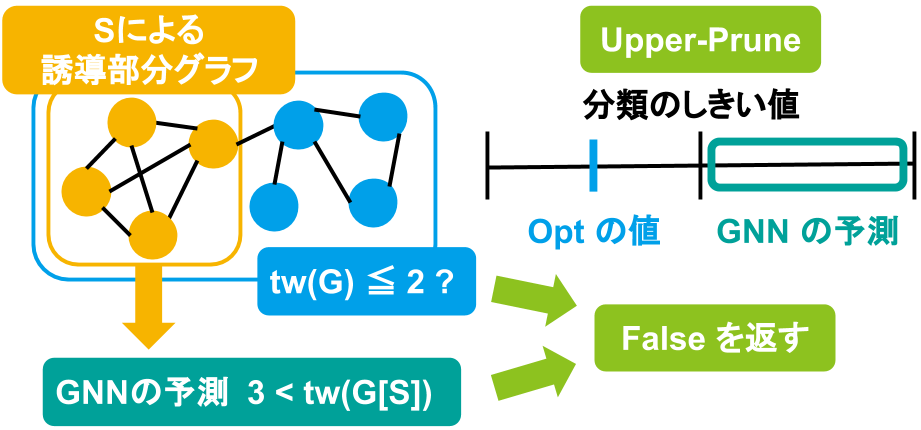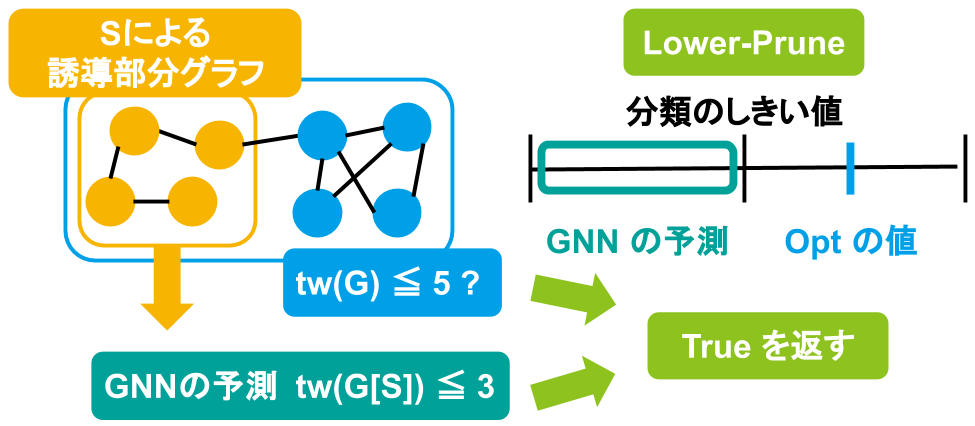この枝刈り方法の利点として、下記の 3 つがあります。

• 先述の Lower-Calculation や Upper-Calculation と適切に組み合わせることで、正確に上界や下界の計算が可能な点
• Softmax Cross Entropy 関数を損失関数に用いモデルを学習させることで、モデルの予測確率を考慮した枝刈りが可能になる点
• 今回の二値分類モデルだけではなく、多値分類モデルを用いる際にも容易に拡張できる点

正確な上界・下界の計算が可能

これら 2 つの枝刈り方法は、先程述べた Lower-Calculation や Upper-Calculation と適切に組み合わせることにより、与えられたグラフに対する木幅の上界や下界を計算できます。前者は Upper-Prune と、後者は Lower-Prune と組み合わせることにより、それぞれ正確に上界と下界を計算できます。

前者について少し説明します。Lower-Calculation のアルゴリズムを、\(opt = |V| – 1\) が入力された場合必ず \(true\) を返すように書き換えます。ここで Upper-Prune において、本来は True であるべき場所で False を返してしまった場合を考えます。これにより、本来はある木幅 \(k\) 以下であると判定されるべき値で、木幅は \(k\) より大きいと判定することとなり、本来よりも大きい値として算出してしまいます。後者についても同様に示すことができます。

モデルの予測確率を用いた枝刈りが可能

Cross Entropy 関数を損失関数としてニューラルネットワークを学習するということは、モデルの出力ベクトルを活性化関数（Softmax 関数）に通した際の各要素が、各クラスへの割り当て確率となるように学習することとみなせます。そのため、出力ベクトルの要素の最大値 \(x_{max}\) に対し、\(x_{max} \geq \mathrm{prob\_bound}\) となる場合にのみ、枝刈りを行うことで、モデルの予測確率が \(\mathrm{prob\_bound}\) 以上である予測のみを考慮でき、最終的に出力する木幅の精度の向上が見込まれます。

多値分類モデルへの拡張が可能

二値分類を行う GNN だけでなく、多値分類タスクに対して訓練済みの GNN を用いる場合にも容易に拡張可能です。また、前述の予測確率を組み合わせることで、さらなる精度の向上が見込まれます。

GNN は木幅に関する分類タスクを適切に学習できるか？

今回導入した 2 つの枝刈りにおいて、GNN による予測性能が重要になるため、分類タスクを適切に学習した GNN が要求されます。しかし、木幅は [12] でも述べられているように、大域的な連結度を表す値であり、近傍の集約を繰り返し特徴ベクトルを更新していく今回の GNN では、木幅に関する特徴を適切に学習できない可能性があります。そのため、まずは木幅に関する分類タスクの実験による検証を行いました。

今回は、しきい値 \(thresh\) に関して \(\frac{|V|}{2}\) を用いる二値分類タスクと、\(\lfloor \frac{5tw(G)}{|V|} \rfloor\) の値でラベル付けした 5 クラス分類タスクを考えました。詳しいハイパパラメータの設定などは後述するコードをご覧ください。

GNN における木幅に関する分類タスク実験の結果

それぞれのタスクにおける実験結果として、テストデータに対する精度の推移を下図に示します。

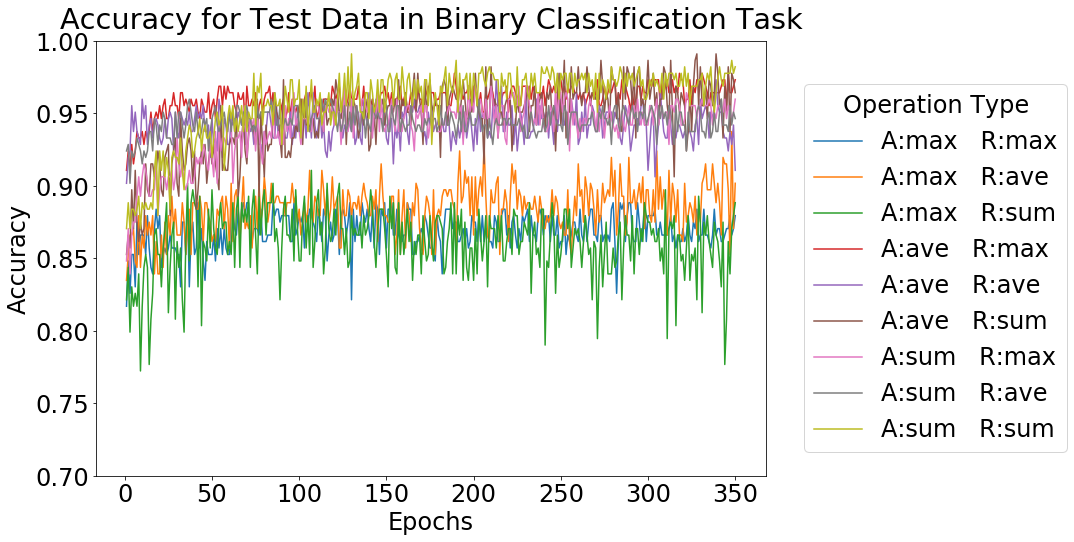
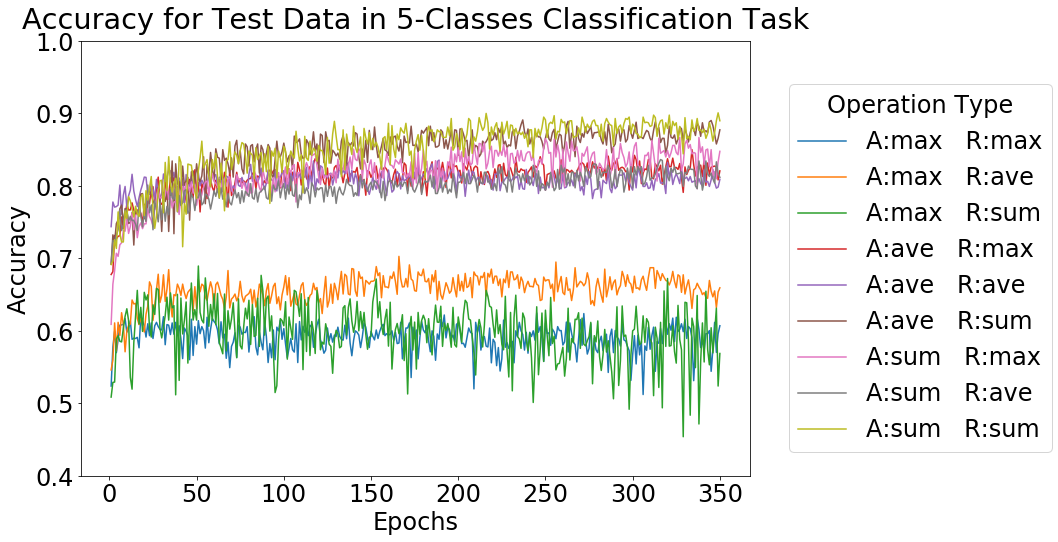
Operation Type における、A は Aggregation、R は Readout の種類を表しています。どちらの場合も、Aggregation に max を使用したもの以外は 9 割前後、8 割前後といった高い精度が得られています。この結果より、GNN は Aggregation, Readout の方法をうまく選択することで、木幅に関する分類タスクを適切に学習できると判断しました。今回用いる GNN モデルにおける Aggregation, Readout の方法として、総合的に精度が良かった、どちらも sum を用いる組み合わせを使用しました。

アプローチ 2

先程は分類タスクに対する GNN を利用しましたが、こちらは直接グラフ回帰問題として GNN により End-to-End で木幅を予測しようというアプローチです。先程の実験結果より、GNN を用いた木幅に対する分類タスクの精度が良く、GNN が、木幅に関する特徴を適切に捉えていると考えました。そのため、End-to-End で予測を行うことで、より精度良い予測が可能になると考えました。しかし先程とは異なり、この方法では正確な上界や下界などは得られません。

今回、アプローチ 1 で用いた GNN 構造により出力されるベクトルの次元数を 32 に変え、続いてそれを 2 層の MLP に入力し、最終的に 1 つの実数値を得るといったネットワーク構造を用いました。詳しいネットワーク構造は後述するコードをご覧ください。

実験結果

アプローチ 1

今回、先程紹介した既存のアルゴリズムと GNN による枝刈りを導入したアルゴリズムの両方を python 3.7 にて実装し、先程のランダムグラフ生成モデルより生成された 50 個のグラフに対し、アプローチ 1 の有効性を検証するための実験を行いました。

今回、GNN による枝刈りを導入したアルゴリズムのうち下記の 3 つを実装しました。

• 上界を求める Upper-Prune と Lower-Calculation を組み合わせたもの（Upper-Alg）
• 下界を求める、 Lower-Prune と Upper-Calculation を組み合わせたもの（Lower-Alg）
• 双方の枝刈りを採用した上で、Lower-Calculation を行うもの（Combine-Alg）

これらと Lower-Calculation ベースの既存のアルゴリズム（Existing-Alg）との比較を行いました。また、グラフの大きさによっては途方も無い時間がかかってしまうことが予期されるため、タイムアウトを 10 分に設定しました。

結果を下図に示します。

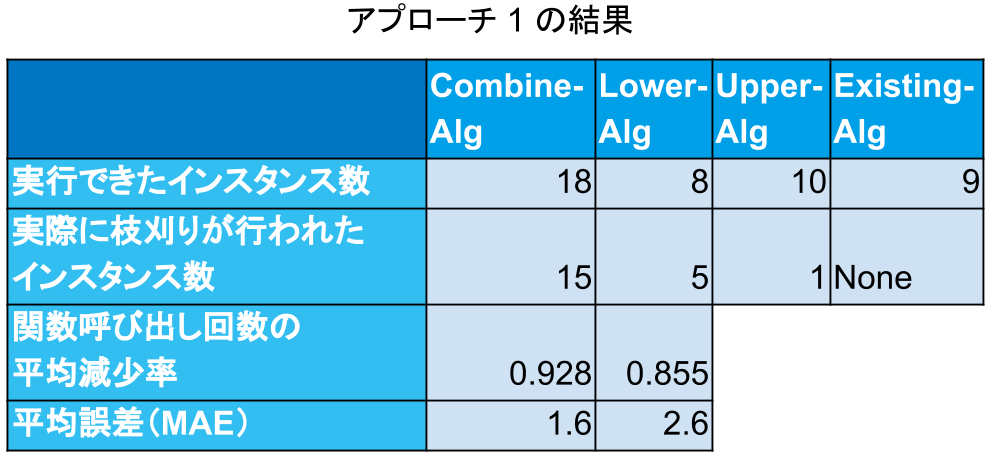
10 分以内に実行が完了したインスタンス数は、既存のアルゴリズムでは 9 となったのに対し、 Combine-Alg では 18 と、既存アルゴリズムより多くのインスタンスに対し計算できていることがわかりました。また Lower-Alg や Upper-Alg ではそれぞれ 8, 10 となり、既存アルゴリズムとほぼ変わりませんでした。

続いて、この枝刈りによりどの程度既存のアルゴリズムが効率よく動作するようになったかを見るために、関数呼び出し回数を比較しました。今回、Upper-Alg で枝刈りが行われたインスタンスは、Combine-Alg や Lower-Alg ではタイムアウトしていたため、Combine-Alg と Lower-Alg に関して、平均の減少率を計算しました。これは、どちらも 9 割前後となり、GNN による枝刈りが効率よく動作していることがわかりました。

また、精度を比較するために、近似解と真の値との絶対値の平均を計算したところ、Combine-Alg では 1.6 、Lower-Alg では 2.6 となりました。より積極的な枝刈りを行う Combine-Alg のほうが精度が良く、直感と反する結果となっているため、今後より多くのインスタンスで実験を行い検証する必要があります。

しかし、表には載せていませんが総合的な実行時間を比較すると、Combine-Alg などで平均よりも多く枝刈りを行っているいくつかのインスタンスを除き、既存のアルゴリズムのほうが実行時間が速いです。これは、GNN の推論に時間がかかっているためと考えられます。多くの場合、総実行時間の 9 割ほどを占めていました。

下記に、どの程度関数呼び出し回数が減少しているかの例として 、2 つのインスタンスに対し、実際のグラフと関数呼び出し回数をプロットした棒グラフを示します。

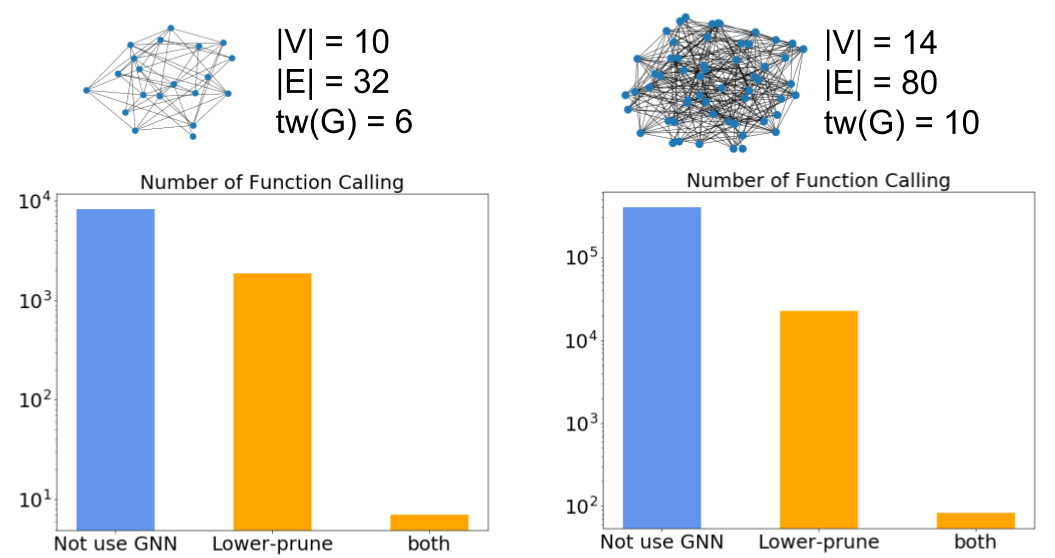
アプローチ 2

テストデータに対する Mean Absolute Error (MAE) の値の推移を下図に示します。

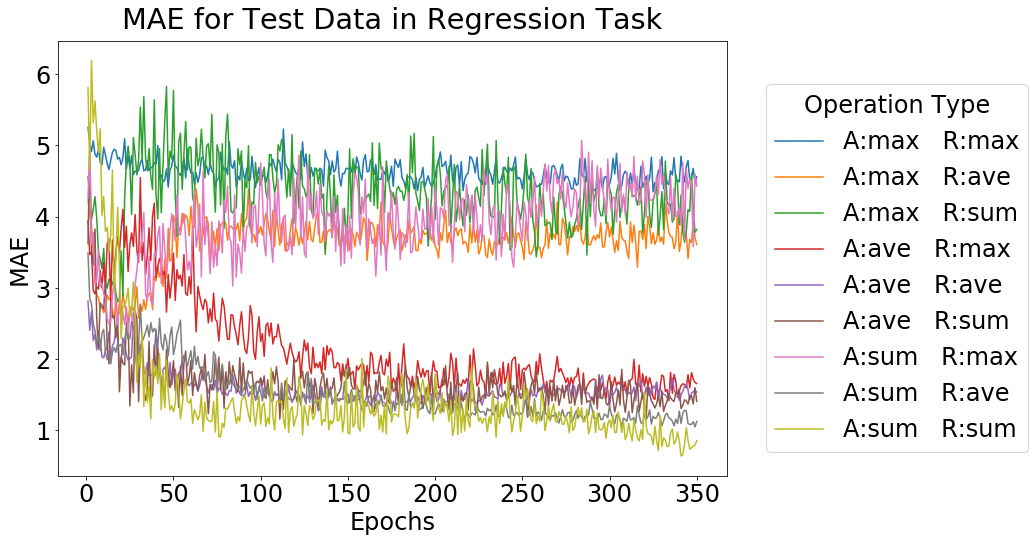
このグラフを見ていただくとわかるように、分類タスクと同様に、Aggregation, Readout ともに sum を用いるモデルが最も精度がよく、最終的な値は 0.75 ほどとなりました。これは、予想したように手法 1 よりも良い結果が得られています。また、テストデータに対し、予測した木幅と実際の木幅をプロットした散布図を下記に示します。左側が GNN （Aggregation, Readout ともに sum を用いるモデル）による結果で、右側が同じデータを用い、頂点数、辺数、平均次数で線形回帰を行った際の結果です。

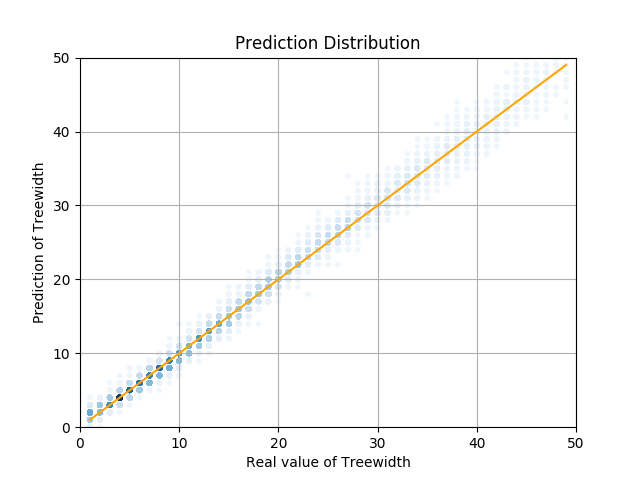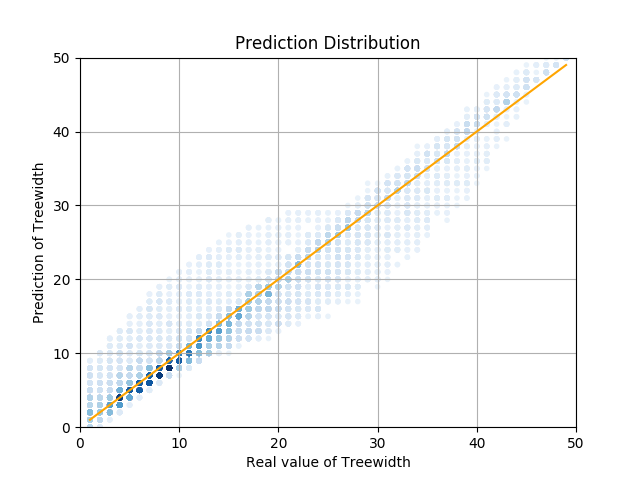散布図を見るとわかるように、大きく外している例は無いことがわかります。これら結果を比較してもわかるように、比較的精度良く予測ができていると考えられます。

まとめ

まず、アプローチ 1 についてですが、いくつかのインスタンスで枝刈りルールがうまく働き、関数呼び出し回数の観点において 90% ほどの減少が見られました。しかし、推論に時間がかかっており、総実行時間の面では改善が見られないインスタンスも多くありました。今回のインターンシップでは推論の高速化については特別には取り組みませんでしたが、推論フレームワーク(例えば Menoh, chainer-trt, chainer-compiler)の利用や各種の最適化によって、ある程度は高速化できる可能性があります。

続いて、アプローチ 2 についてですが、平均絶対誤差が 0.75 ほどのモデルが学習でき、いくつか計算が容易なグラフ不変量を用い線形回帰を行った結果と比較し、精度よく予測ができていました。

今後の課題として、より素早く正確に推論が可能なモデルや推論フレームワークを使用すること、素早く計算が終わる状態から探索木を展開していくために、探索順序を学習させ高速化を図るなどがあります。また、ハイパパラメータのチューニングなどは一切行っていないため、ハイパパラメータのチューニングなどで更に精度が向上すると考えています。

今回、実験に使ったコードはこちらにまとめられています。もし、興味がありましたらご覧ください。

インターンシップ全体を通しての感想ですが、今回取り組むテーマとして選んだこの課題は、自分で興味を持ったテーマを選んだため、結果が出るかどうかがわからなく不安なことも多くありましたが、メンターの酒井さんや劉さん、並びに他の社員の皆さんやインターンの皆さんに助けられながら、なんとかここまで進められました。お世話になった皆様、本当にありがとうございました。

参考文献

1. Hans L. Bodlaender, Arie M. C. A. Koster, Combinatorial Optimization on Graphs of Bounded Treewidth, The Computer Journal, Volume 51, Issue 3, May 2008, pp. 255–269.
2. Paul Erdős and András Hajnal, On chromatic number of graphs and set-systems,  Acta Mathematica Hungarica, 17.1-2, 1966.
3. Manuel Sorge,  The graph parameter hierarchy, 2013.
4. Ziwei Zhang, Peng Cui and Wenwu Zhu, Deep learning on graphs: A survey, arXiv preprint, 2018.
5. Thomas N. Kipf and Max Welling, Semi-supervised classification with graph convolutional networks, ICLR 2017.
6. Keyulu Xu, Weihua Hu, Jure Leskovec and Stefanie Jegelka, How powerful are graph neural networks?, ICLR 2019.
7. Holger Dell, Thore Husfeldt, Bart M. P. Jansen, Petteri Kaski, Christian Komusiewicz and Frances A. Rosamond, The First Parameterized Algorithms and Computational Experiments Challenge, IPEC 2016.
8. Holger Dell, Christian Komusiewicz, Nimrod Talmon and Mathias Weller, The PACE 2017 Parameterized Algorithms and Computational Experiments Challenge: The Second Iteration, IPEC 2017.
9. PACE-challenge/Treewidth: List of Treewidth solvers, instances, and tools, https://github.com/PACE-challenge/Treewidth
10. Tamaki, Hisao. Positive-instance driven dynamic programming for treewidth, ESA 2017.
    著者実装 https://github.com/TCS-Meiji/PACE2017-TrackA
11. Hans L. Bodlaender, Fedor V. Fomin, Arie M. C. A. Koster, Dieter Kratsch, Dimitrios M. Thiliko. On exact algorithms for treewidth, ACM Transactions on Algorithms, Vol 9, 1, Article 12, 2012.
12. 河原林 健一, グラフの木分解と木幅に関する研究とグラフマイナー, 数学, 2015, 67 巻, 4 号, p. 337-355, 2017.
13. 木分解とグラフ・アルゴリズム (最適化と数え上げ) – IBISML 2008,  岡本 吉央
14. Woeginger, Gerhard J. “Exact algorithms for NP-hard problems: A survey.” Combinatorial optimization—eureka, you shrink!. Springer, Berlin, Heidelberg, 2003.

---

メンターからのコメント

メンターを担当したPFNの酒井と劉です。

当初こちら側では、組合せ最適化問題に機械学習・深層学習を応用するようなテーマを考えていたのですが、中野さんから「直接計算するのが難しいグラフの不変量をGNNを使って予測できないか」という提案を受け、劉のグラフアルゴリズムに関する知識や興味もあって、トントン拍子に決まったのが今回のテーマです。

最初は、「木幅は大域的な性質なので、GNNによる予測はあまりうまく行かないのではないか」と予想していて、そういう結果が出たときに、それをどう改善したり問題を単純化すれば解けるのかを考えていくことになると想定していたのですが、中野さんに一通りの実装と最初の実験をしてもらってみると、想像以上の精度で予測することができ、メンター二人もとても驚きました。

インターンシップの限られた期間では、より本格的なアルゴリズムへの組み込みや、現実的な応用方法については踏み込むことは出来ず、それらは今後の課題になりますが、今回の結果だけでも非常に面白い結果だと考えています。