Blog
本記事は金融チームインターンの仲吉朝洋さんによる寄稿です。
背景
金融分野において、現実的な金融時系列を生成できると取引戦略の学習やポートフォリオ構築のように多くの応用があります。また,過去の時系列で条件付けした上でもっともらしい続きの時系列を生成することができれば,予測に活用することも可能だと考えられます.
その金融時系列生成に拡散モデルを用いた先行研究としては,「CSDI: Conditional Score-based Diffusion Models for Probabilistic Time Series Imputation」・「拡散モデルを用いた条件付き金融時系列データ生成」・「拡散モデルの金融時系列生成への応用」などがあります.
これらの研究で用いられている拡散モデルは,少なくとも明示的には v-prediction を採用していません.
そのため,今回は v-prediction を用いることによる金融時系列生成への影響について調べました.
v-predictionについて
v-predictionは、「Progressive Distillation for Fast Sampling of Diffusion Models」内で拡散モデル蒸留の文脈で提案された手法です.
「Imagen Video」のような画像・動画生成に対する拡散モデル等で使われており,収束の早さや生成物の質の向上,学習の安定性について報告されています.
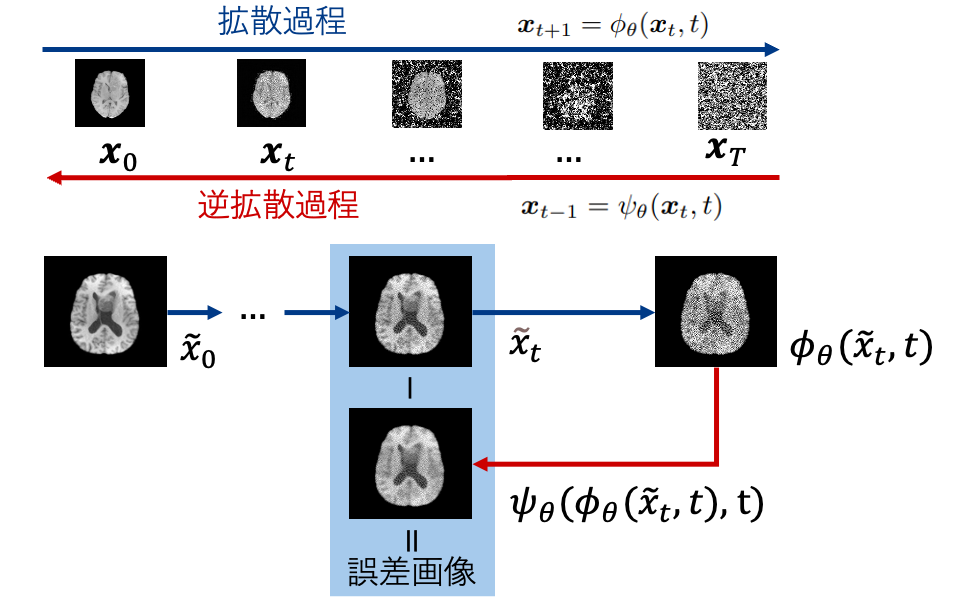
一般的な拡散モデルが行っているのはノイズを予測する ε-prediction ですが,v-predictionは直接ノイズを予測するのではなく,ノイズと生成したいデータの線形結合によって定まる値を予測します.直感的には,データが球面上に埋め込まれていると考え,ノイズから生成物への球面上の速度のようなものを予測します.ε-predictionでは,生成初期の完全なノイズと終盤の生成物に近づいている状態では予測したいノイズの大きさが異なります.一方で,v-predictionでは予測したい速度のノルムはほとんど一定になります.
そのため,ノイズの割合が非常に高い領域でも v-prediction は ε-prediction に比べうまく機能します.
金融時系列生成への v-prediction の活用
金融時系列は画像などとは異なり,生成物自体もノイズに近い性質を持ちます.そのため,ε-prediction では学習が安定しなかったり,金融時系列の特徴を捉えられない可能性があります.一方で,v-predictionであれば予測したい速度のノルムが安定するため,生成物がノイズに似ていることが問題とならないことが考えられます.
また,金融時系列生成の結果を用いて予測を行う場合,高速に計算できることが望ましいですが,拡散モデルによる生成はステップ数が多いと時間がかかってしまいます.そこで,v-predictionを採用すると生成ステップ数を減らしても十分な性能を維持することが期待できるとされています.
そのため,本研究ではその点についても検証を行います.
モデルと評価手法
速度予測部分は「CSDI: Conditional Score-based Diffusion Models for Probabilistic Time Series Imputation」のアーキテクチャを参考にし,v-prediction を採用したモデルを実装しました.
そして,TOPIX500の日足データで前半64日のリターン列を入力として後半64日のリターン列を生成するタスクで学習を行いました.
評価については,生成された時系列が stylized factsをどれだけ再現しているのかと,生成物を用いた t 日後のアップダウン予測性能について比較しました.
比較はε-predictionとv-predictionのそれぞれについて,生成過程が10ステップと20ステップであるもの両方に対して行いました.ただし,ステップ数の差は蒸留によるものではなく,最初からそれぞれのステップ数に固定して学習しています.
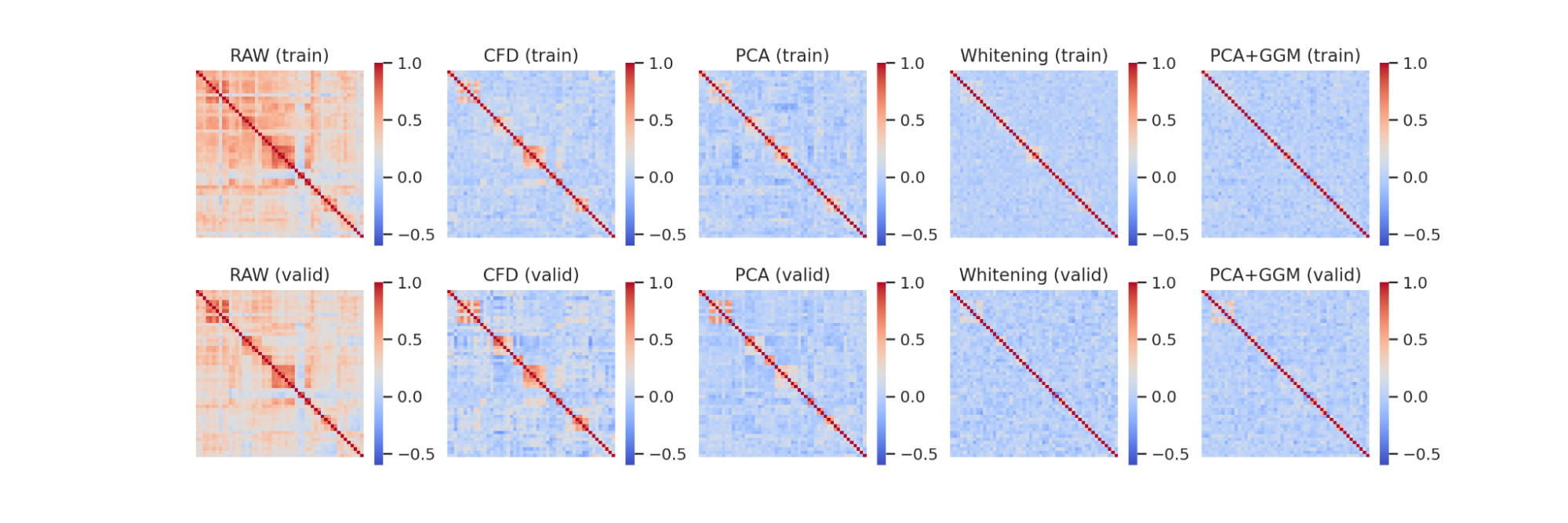
まず,stylized factsでは歪度・尖度・volatility clusteringを対象としました.金融時系列が従う分布は正規分布ではないことが知られているため,歪度と尖度によってリターン分布の再現性を確認します.volatility clusteringは価格変動の大きさが時期によって似通うという性質です.今回は各入力に対して前半64日と後半64日の標準偏差を計算し,その間の相関係数を指標として用います.
また,アップダウン予測では,まず1つの入力に対して n サンプル生成します.その後,リターン列を価格列に直し,前半の64日目の価格に対して後半の t 日目の価格中央値が大きいか小さいかによって予測します.今回は n を 11 とし,t としては 1, 2, 4, 8, 16, 32, 64を用いました.
データセット
TOPIX500の日足データを用います.期間は 2006年11月29日から2023年12月29日までで,学習・バリデーション・テストにはそれぞれ8:1:1の割合で分割しました.その中から,連続した128日間の取引日でのリターン列を学習データとしました.銘柄同士の区別は行わずに,1銘柄の128日間が1つのデータになります.
結果
stylized factsとリターン分布
各手法とパラメータに対する stylized facts は次表の通りです.尖度は 3 を引く定義を採用しています.
この結果を見ると,尖度とvolatility clusteringの値については20ステップの v-prediction が実データの値に近くなっています.しかし,歪度については 10ステップの v-prediction の方が近く,20ステップの v-prediction の値は最も離れています.
歪度が同程度の値の10ステップのε-prediction に比べると、20ステップのv-predictionは、尖度とvolatility clusteringの点で優れているように見えます.
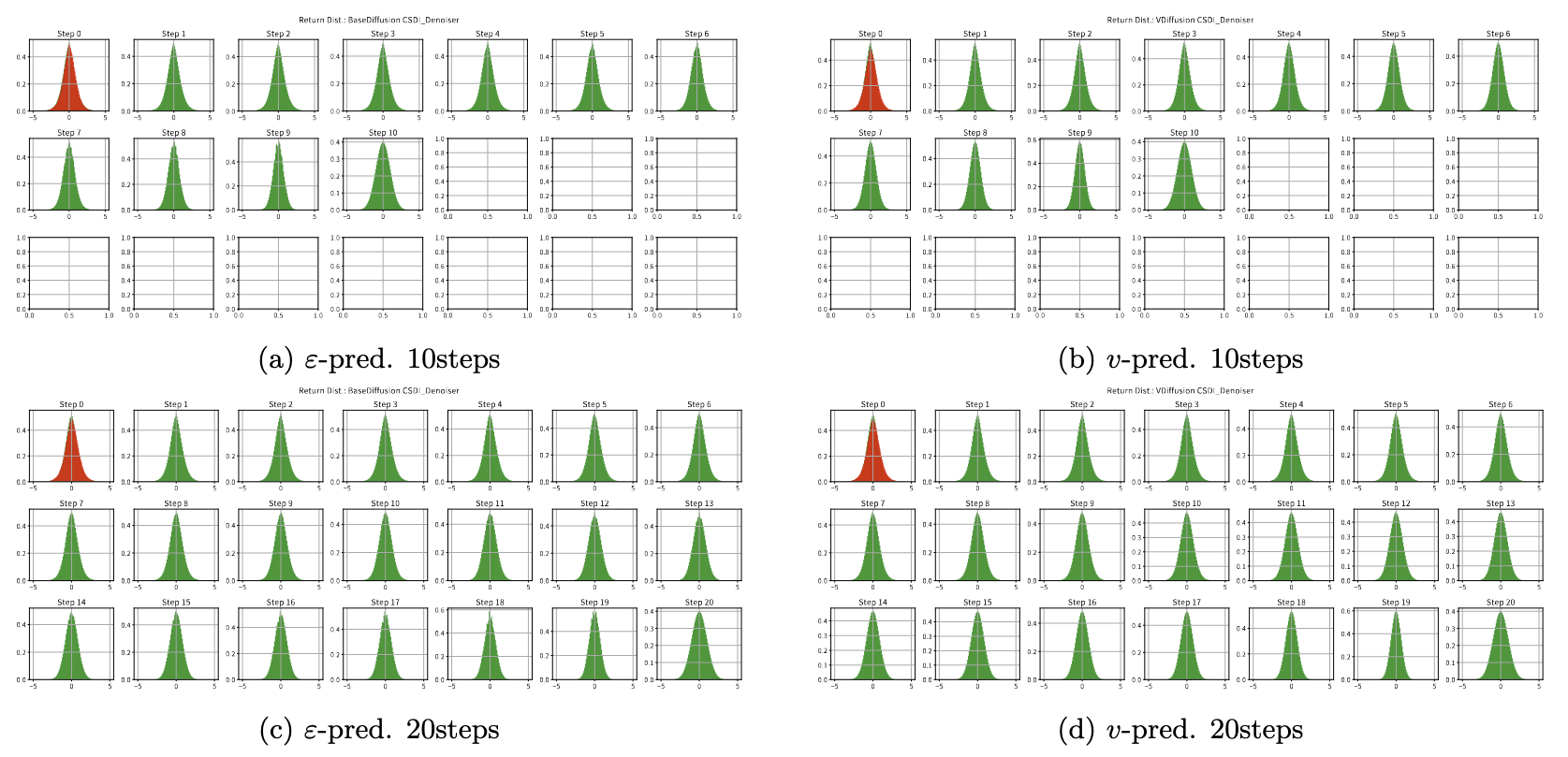
また,その下の図はそれぞれが生成したリターンの分布です.ステップ数がもっとも大きい分布は拡散モデルによる生成を始める直前のノイズに対応しており,正規分布になっています.そこから,左上のstep 0に向かって生成が進んでいきます.緑色が拡散モデルによって生成されるデータで,赤色が実データの分布を表しています.
この分布を見ると,stylized facts で大きく優れているわけではない ε-prediction の10ステップがもっとも実データの分布を近似できているように見えます.
| 手法 | ステップ数 | 尖度 | 歪度 | volatility clustering |
|---|---|---|---|---|
| 実データ | — | 6.319 | 0.2246 | 0.5998 |
| ε-prediction | 10 | 5.849 | 0.09362 | 0.6673 |
| ε-prediction | 20 | 5.271 | 0.1215 | 0.6486 |
| v-prediction | 10 | 7.051 | 0.1476 | 0.5867 |
| v-prediction | 20 | 6.586 | 0.09257 | 0.5753 |
アップダウン予測
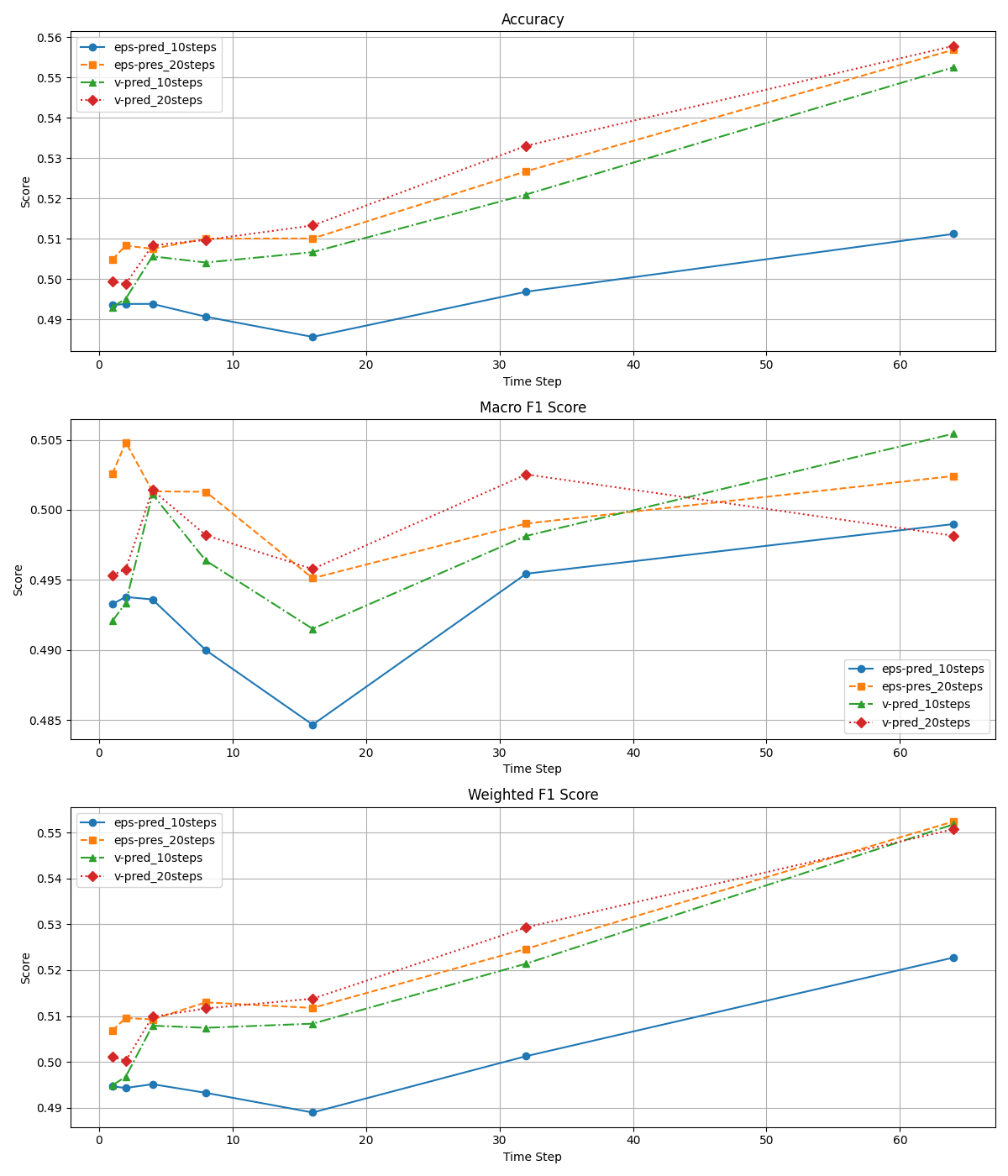
それぞれの手法とステップ数でアップダウン予測を行った際の精度・マクロF1値・重み付きF1値は下図のようになります.
精度と重み付きF1値については20ステップのε-predictionとv-predictionでは大きな差はありません.
一方で,ステップ数を10に減らしたときの性能に関してはε-predictionでは大幅に低くなっているのに対し,v-predictionの場合は性能低下が抑えられており,10ステップ同士で比較するとv-predictionが大きく勝る結果となっています.
結論・今後の展望
金融時系列生成を行う拡散モデルに v-prediction を適用しました.その結果,stylized facts に関しては,stylized factsで上げた3つの指標のうち2つの指標で最も良い再現度を示しました.
また,アップダウン予測については,マクロF1値を除き,ステップ数が多い場合には大きな性能差は見られませんでした.
一方で,生成ステップ数を少なくした際には v-prediction の性能はほとんど低下せず ε-prediction よりも性能が高くなることを確認できました.
このことから,拡散モデルによる金融時系列生成を時系列予測に応用する際に,v-prediction を採用してステップ数を減らすことによって,より高速な計算が可能になると考えられます.
今後の課題としては,今回はノイズや速度の予測を行うモデルのアーキテクチャ部分を触っていないため,v-predictionに適したアーキテクチャの模索が一つ目に挙げられます.
また,生成ステップ数についても,より多くした場合や少なくした場合に性能差にどのように表れるかが不明で、その分析が今後の課題に挙げられます。
Area