Blog
吉田です.
先日,博士論文の公聴会が終わりました. タイトルは「次数を制限したグラフと制約充足問題に対する定数時間アルゴリズムの研究」というものでした. また,博士課程での研究の成果が認められて,日本学術振興会から育志賞という賞を頂くことになりました. こちらは他の受賞者の研究内容が分からなさ過ぎて凄いですね. 今後もPreferred Infrastructureにはアドバイザーの様な形で勤めることになると思いますので宜しくお願い致します.
ということで博士課程の終わりも近く,良い区切りですので, これまで専門に研究してきた定数時間アルゴリズムについて簡単に話をすることにします.
定数時間アルゴリズムは,その名のとおり入力長に依存しない計算時間で動作するアルゴリズムのことです. 普通に考えてそんなアルゴリズムはあり得ないように思えますが,どうすればそんなアルゴリズムが実現出来るでしょうか.
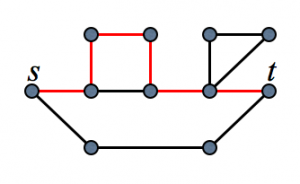
例えばグラフが連結かどうか調べたいとしましょう. 普通の判定問題で有れば,グラフが連結であればYes,そうでなければNoと答えなければいけません. 当然これを正確に答えるにはグラフを全て見なければならず,線形時間が必要です. そこで判定問題の条件を次のように緩めることにします. つまり,グラフが連結であればYes,グラフが連結には“程遠ければ”Noと答えることにします. どちらでも無ければ何を出力しても良いことにします. これをグラフの連結性の“検査”と呼ぶことにします. “程遠い”には色々な定義が考えられると思いますが,ここでは,グラフの頂点数を\(n\),許すエラーの割合を表すパラメータを\(\epsilon\)として, グラフを連結にするのに\(\epsilon n\)本の枝を足さなければならないことと定義しましょう. 言い換えると,グラフ中に連結成分が\(\epsilon n – 1\)個有るということです. この様に,連結では無いけれど,連結に近いグラフに対する判定を諦めることで,代わりに計算時間を少なくしたい,願わくば定数時間にしたいというのが性質検査の目的の一つです.
グラフの連結性を検査するアルゴリズムとしては次の様なものが考えられます. 計算時間が定数であることや,アルゴリズムの正しさの証明はここではしませんので, 興味が有れば考えてみてください(証明は多分5行とかで済みます).
- \(c\)を十分大きな定数とする.
- \(S\)を大きさ\(c/\epsilon\)のランダムな頂点集合とする.
- 各\(v in S\)に対して,
- \(v\)から\(c/\epsilon\)頂点だけ幅優先探索(BFS)する.
- もし大きさ\(c/\epsilon\)の連結成分が見つかったらNoと出力.
- Yesと出力.
歴史的には性質検査は確率的検査可能証明(PCP)と呼ばれる理論計算機科学の中の大道具の中の一要素として開発されてきました. 細かいことを抜きにすると,PCP = NPであることが知られており, NPよりもPCPの方が扱い易い形をしているので,PCPを利用して様々な問題の近似困難性を示すのに用いられてきました. 例えばMax 3SATと呼ばれる最適化問題は,任意の\(epsilon >0\)に対して\(7/8+epsilon\)近似をするのは不可能ということがPCPを用いて証明されています. そのPCPの中で,関数の性質の検査が非常に重要な位置を占めており,関数に対する検査アルゴリズムが色々と開発されてきました. 余談ですが,関数に対する性質検査からアイデアを借りて問題にしたのが,2011年京都大学プログラミングコンテスト(KUPC)の問題Gです.
さて,私が博士課程で目標としていたのは「どのような性質であれば定数時間で検査出来るか,その必要十分条件を知りたい」ということです. 見ての通りかなり理論寄りな話です. 対象にしたのはグラフと制約充足問題というかなり広い範囲です.
グラフに対しては,必要十分条件を得る所までは出来ませんでしたが,ある程度理解を深めることが出来たと思います. ここで書くには成果が込み入っているのでこちらは省略します.
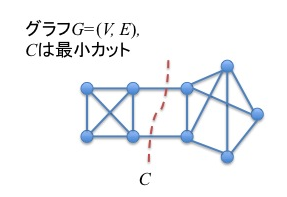
制約充足問題に関してはかなり成功しました. 制約充足問題とは,変数の集合と制約の集合が入力として与えられ,変数に値を代入して変数の間の制約を全て/出来るだけ多く満たすというものです. 例えば,グラフの\(k\)彩色性,\(k\)SAT,有限体上の線形連立方程式などが制約充足問題で表現できます. ここでは検査したいことは,与えられた入力の全ての制約を充足出来るかどうかです. この問題に対して定数時間で検査可能な制約充足問題の必要十分条件を得ることが出来ました. 必要十分条件の雰囲気としては「局所的に入力を見るだけで充足性の判定が出来るような制約充足問題なら検査も簡単,そうでなければ難しい」です.
折角ですので公聴会で使ったスライドを以下に載せておきます.
私の名前の「吉」は本当は「土+口」で,slideshareにはそのフォントが無いからか「吉」が消えてしまっていますね…
さて,最近は次の目標はどうすべきかということを考え始めています. 博論でやり残した理論的な課題は色々有るので,それはぼちぼち片付けることになるでしょう. 知識も蓄えていますし,似た研究をしている研究者の友人も沢山いるので取っ付き易いです. けれども出来れば,今までの積み重ねを基に,他のトピックに手を出したいなと思っています. 特に,折角定数時間アルゴリズムは実用性のポテンシャルを持っているのに,これまでに作られた定数時間アルゴリズムはどれも実用的ではないのが気になっています. 例えば性質検査の基本的な考え方は「エラーを許す代わりに計算時間を抑える」ですが,計算時間を定数にまで押さえる為に無理をしたせいで, 定数になったその定数が大きすぎて実用には程遠いということになってしまいました. これでは悔しいので,ちょっとぐらい入力長に依存してよいので,実用的に速いものが作れないかなと思います. 実際,機械学習の分野ではそういった話がチラホラ出てきているようです.
Preferred Infrastructureを設立したそもそもの動機は,研究の世界と実用の乖離が激しいので,その間を埋めようというものでした. 会社自体は実用の立場に立って研究の世界からアイデアを借りてくることになると思いますが,僕はその逆の研究の立場から間を埋めていきたいと思います.
Tag