Blog
本記事は,2022年夏季インターンシッププログラム「JE06. Matlantis向けの物性値計算アルゴリズムの開発」で勤務された竝河 伴裕さんによる寄稿です.なお,本研究で開発された技術については現在特許申請中です.
はじめに
2022年度夏季インターンシップに参加した東京大学新領域創成科学研究科の竝河 伴裕と申します. 今回のインターンシップでは,Matlantisで提供されているニューラルネットワークポテンシャル(NNP)であるPreFerred Potential (PFP)を用いた高速な結晶構造予測と,予測効率を向上するための手法開発について取り組みました.
背景
結晶構造予測
結晶構造予測とは,結晶の組成式,圧力,温度などから結晶内の原子配置および単位格子の形を推測するものです [1]. 実験により構造を同定するのは時間的コストがかかるため,計算により結晶構造予測ができれば,新規材料開発を加速させることが期待できます.
この問題は,数学的には,原子配置と単位格子の形をパラメータとした自由エネルギー最小化として捉えられます. これまで用いられてきた代表的な手法として,密度汎関数理論(Density functioanl theory,DFT)計算で構造のエネルギー評価を行い,遺伝的アルゴリズムを用いて最適な構造の探索を行う,という手法があります.この方法はこれまで,多くの成功例が報告されてきました [1,2].
結晶構造予測には遺伝的アルゴリズムがよく用いられます.まず,ランダムに初期候補構造群を生成します.各構造についてエネルギー評価を行います.評価されたエネルギーをもとに,有望だと思われる構造をいくつかピックアップして,交叉(cross over)や変異(mutation)させることにより新たな候補構造群を作ります.各ステップで生成される候補構造群を世代(generation)と呼びます.これらの手順を繰り返しエネルギーを最小化することで,エネルギーが低い=現実世界に存在する安定構造を見つけます.
エネルギーを評価する手法として通常はDFTを用いるのですが,DFT計算は計算コストが大きいため,結晶構造予測は非常に時間のかかるものでした.そこで,近年ではDFTの出力を学習させたNNPを用いて,結晶構造予測を高速化する取り組みが行われています[3].
今回はPFPを用いることで高速化を図りました.PFPは,Matlantis (https://matlantis.com/ja/) 上で提供されている様々な原子に対応しているNNPです[4].多種多様な元素の組み合わせおよび配置に対して,高速かつ高精度でDFTの再現をするよう設計されています. これまでの結晶構造予測にNNPを用いている先行研究では,通常計算したい系のDFTデータを収集して専用のNNPを構築していました.一方,PFPは多くの元素や不安定な構造にも汎用に使えるよう設計された訓練済みモデルであるため,専用のNNPを用意する必要がありません.
PFPを用いた結晶構造予測
遺伝的アルゴリズムとPFPを組み合わせた手法を実装して,炭素単体の結晶構造予測に用いた結果,図1,2が示すように,現実で観測される結晶構造の予測に成功しました. 低圧下ではグラファイトが安定で,高圧下ではダイアモンドが安定であることを再現できています. また,表1ではPFPとDFTそれぞれを用いた場合の計算時間を比較しています.PFPを用いることで大幅に計算時間が短縮されていることがわかります.
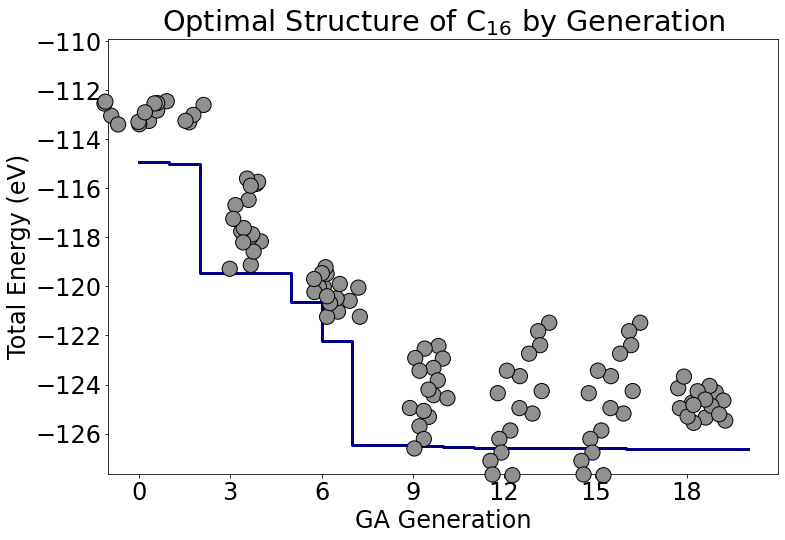
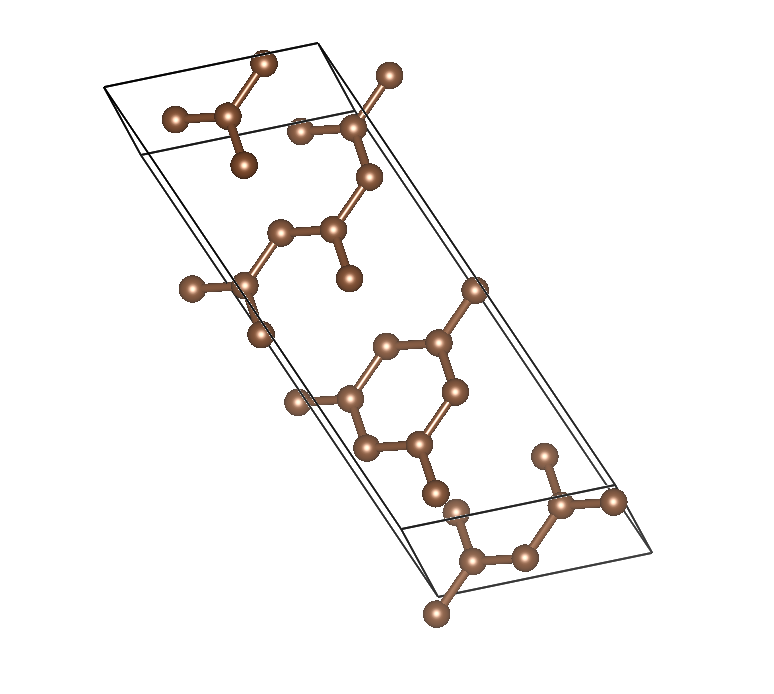
図1. 圧力P = 0, 温度T = 0, 炭素原子16個の場合の結晶構造予測. (上) 遺伝的アルゴリズムが進むにつれ結晶が予測できる様子. (下) 最終的に予測された構造. グラファイトが得られている.
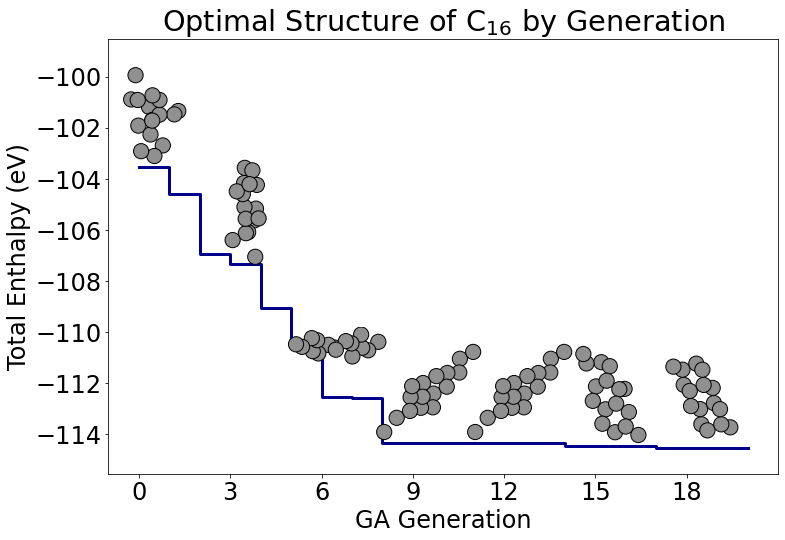
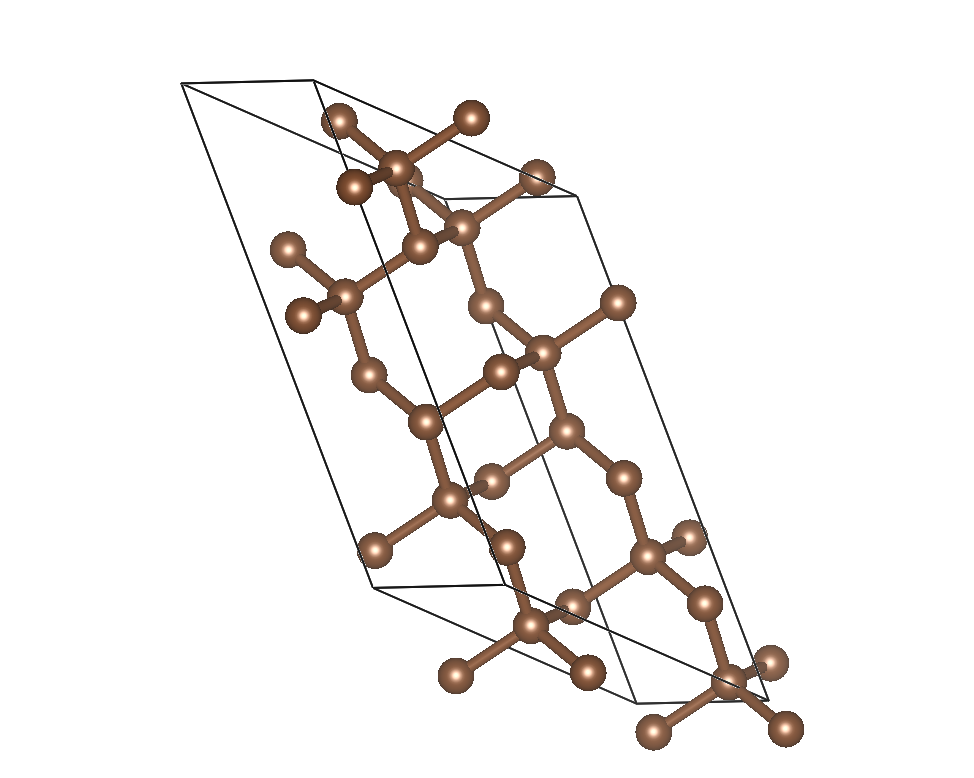
図2. 圧力P = 16GPa, 温度T = 0, 炭素原子16個の場合の結晶構造予測. (上), 遺伝的アルゴリズムが進むにつれ結晶が予測できる様子. (下)最終的に予測された構造. ダイアモンドが得られている.
表1. 圧力 P = 16GPa, 温度 T = 0, 炭素原子16個の結晶構造予測におけるエネルギー計算時間. DFTでの計算時間は, PFPの呼び出し回数と, DFTの1回の計算時間(60秒と仮定)から推定した.
| PFP | DFT(推定値) | |
| エネルギーの計算回数 | 104900 | 104900 |
| 計算時間 | 7306秒 | 6294000秒 |
問題点
現状の結晶構造予測手法の実用化する上で,以下のような問題点が考えられます.
問題点1:
現実で存在可能な構造が探索できない場合があります. 遺伝的アルゴリズムは準安定な構造も得ることができるアルゴリズムです. しかし, 図1で行った圧力P = 0,温度 T = 0,炭素原子16個の結晶構造予測の際に,最安定な構造候補としてグラファイトを得ることはできましたが,準安定な構造の候補の中にダイアモンドの構造を得ることはできていませんでした. ダイアモンドは低圧下でも現実世界に存在していることを考えると,ダイアモンドの構造もこの結晶構造予測において得られることが望ましいです.
問題点2:
NNPなどの近似手法を用いてエネルギー予測を行った場合に,誤差により安定性評価がひっくり返ってしまう可能性があることです. PFPは幅広い系に対して精度が出るよう訓練されているものの,細かいエネルギーの評価には機械学習特有の予測誤差が影響してしまいます. 図3は,2つのエネルギーの近い構造間のPFPおよびDFTでの計算値が矛盾している例です.
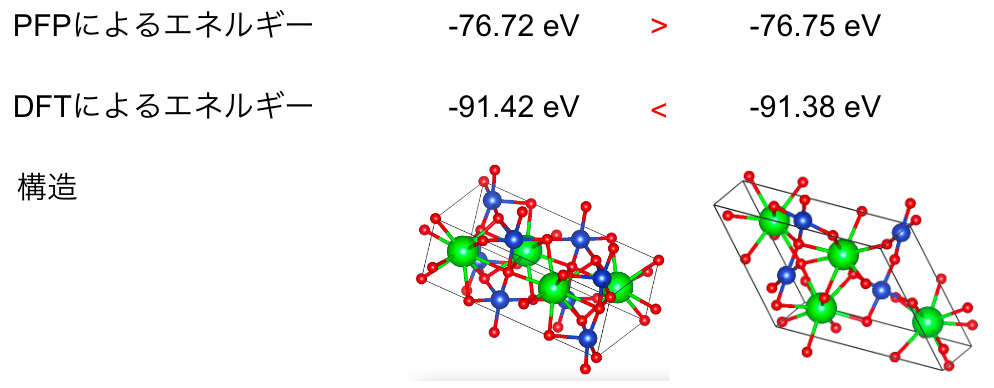
図3. Sr2Cu2O5のPFPとDFTによるエネルギー比較
目標
これらの問題点を改善するため,遺伝的アルゴリズムの実行方法や後処理へ工夫を行うことでなるべく効果的に候補を発見する手法を開発します.具体的には,網羅性(実在する構造をできるだけ多く探索する)および適合率(正確性,発見した構造の何割が実在する構造か) を改善していきます.
網羅性の改善は問題点1の解決を目的としています.結晶構造予測で最終的に得られた上位候補群のなかになるべく多くの準安定構造が含まれることを目指します.
一方,適合率の改善は,DFTによる再計算と組み合わせることで問題点2を解決します.従来のNNPによる結晶構造予測の研究では,見つかった構造からエネルギーの低い順にいくつかピックアップし,DFTで再計算し,エネルギーの大小比較を正確に評価し直すという方法がとられています.しかし,DFTによるエネルギー計算はNNPに比べて莫大な計算コストがかかります.そこで,なるべく再計算対象の候補数を抑えるために,適合率を高めることが重要です.
なお,以下の説明ではすべて,圧力 P = 0,温度 T = 0,炭素原子が単位格子内に8個入っているという問題設定を取り扱います.
手法の性能評価手法
“実現可能な構造をできるだけ探索できる”ことを評価するため,物質材料のデータベースををGround truthと仮定して用いる評価手法を考えました. 今回はデータベースとして,Materials Project [5]を用いています.
データベースを用いた評価
A = {マテリアルズプロジェクト上の構造},B = {遺伝的アルゴリズムで得られた構造}として,
再現率 = \(\frac{n(A \cap B)}{n(A)} \), 適合率 = \(\frac{n(A \cap B)}{n(B)} \)
と定義しました. 再現率は探索の網羅性,適合率は探索の効率性を評価する指標として用いることができます.
類似性判定の手法
データベースを用いた評価において,探索で得られたある構造とデータベース上のある構造が一致することを判定する必要があります. 結晶格子のとり方が必ずしも一致しないため,判定は自明ではありません.今回は, 双方を圧力P = 0,温度 T = 0で構造最適化をした後に,Oganovのフィンガープリント[6]を計算し,それらの cos類似度が一定以下であれば同じ構造だとみなすことにしました. Materials Project上のある構造を基準に,同じ組成の他の結晶同士をOganovのフィンガープリントで比較すると,図4のようなヒストグラムが得られ,最小値が約0.01であったことから,cos類似度が0.01未満であったときに一致したと判定すれば多くの場合で妥当だと考えます.
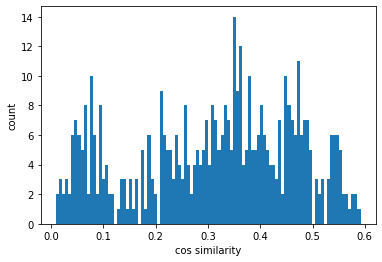
図4. マテリアルズプロジェクト上の構造のcos類似度
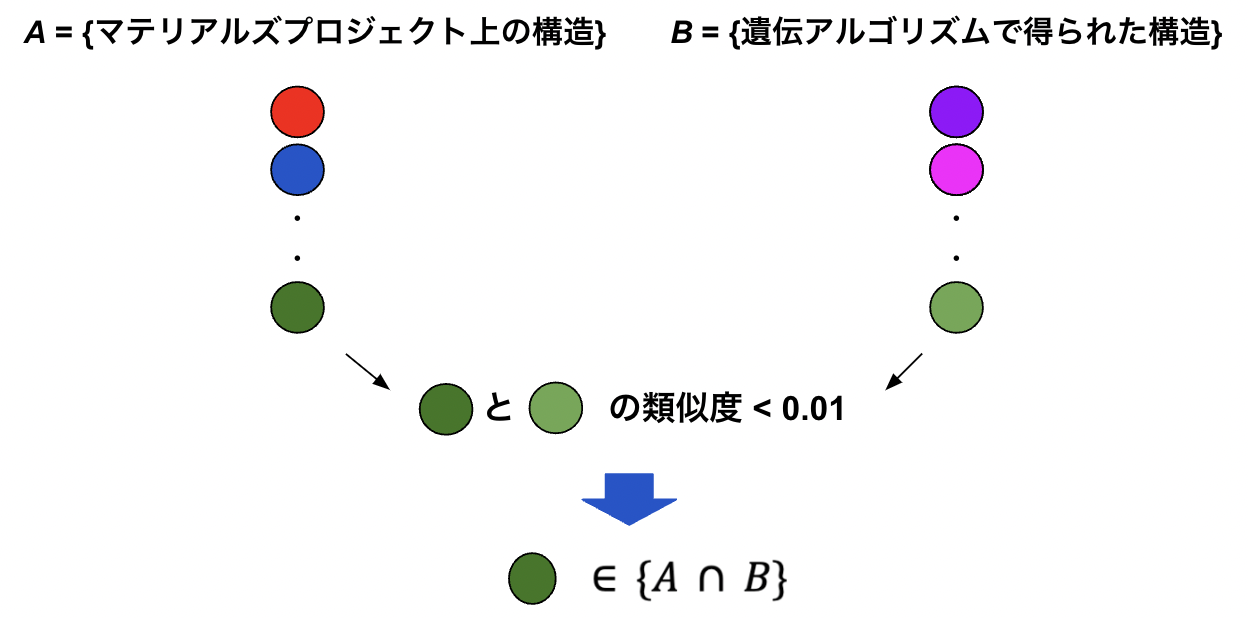
図5. データベースを用いた構造評価の様子
提案手法1:様々な圧力下における遺伝的アルゴリズム
手法:
遺伝的アルゴリズムの各世代で得られる構造を観察したところ,密度が低い構造が好んで探索される傾向にあることが判明しました.これは,構造の周囲のポテンシャル面がなだらかで探索が到達しやすいためであると考えられます.一方,原子間距離が近い高密度な構造は構造を少し変化させるとエネルギーが急激に上昇するような,ポテンシャル面の深い谷にいます.しかし,実在する準安定構造は高い密度を持っていることが多々あります.
そこで,候補に多様性を持たせ,再現率を高めるために,様々な圧力下で構造最適化をする方法を考えました. 結晶構造予測では圧力を高く設定するほど,高密度構造がエネルギー(エンタルピー)評価で優位になり,探索されやすくなります.そこで,通常はその物質の置かれている圧力を設定するのですが,あえてその付近の様々な圧力も設定することで様々な密度の候補を探索しようというものです. 圧力の変化のさせかたにはいくつかの方法が考えられますが, “世代毎に圧力を変化させる” ものと,“複数の固定した圧力で計算する” ものを試しました.
“世代毎に圧力を変化させる方法” では,図6のように,遺伝的アルゴリズムの世代毎に,構造最適化で用いる圧力を変化させます. 変化させる際に,個体群の構造も新しい圧力に構造最適化する必要があるため最適化ステップ数が伸びて計算量が少し大きくなりますが,多様な結晶を探索することが期待されます. 圧力は毎回ランダムに変えるようにしました.
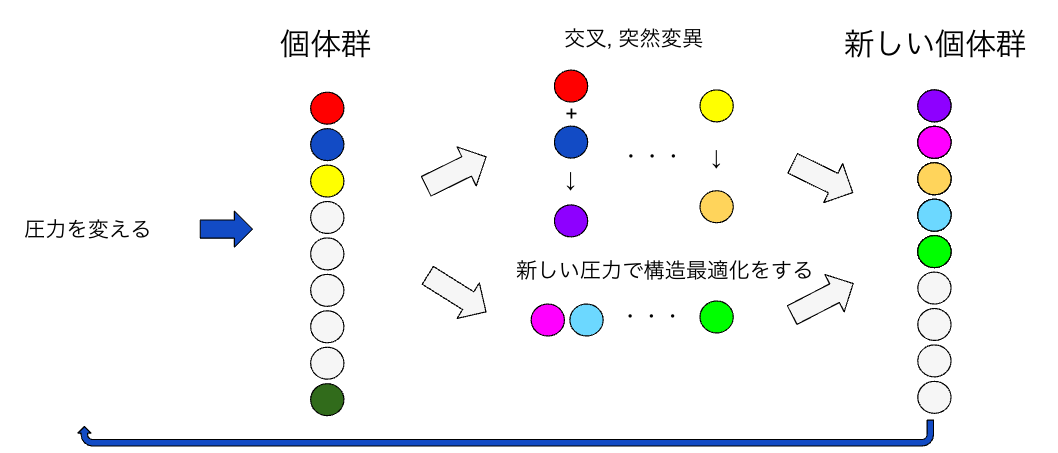
図6. 世代毎にランダムに圧力を変えるアルゴリズム
一方,“複数の固定した圧力で計算する” 方法では,図7のように構造最適化で用いる圧力を複数設定し,それぞれ独立に遺伝的アルゴリズムを回したた結果を合算しました.
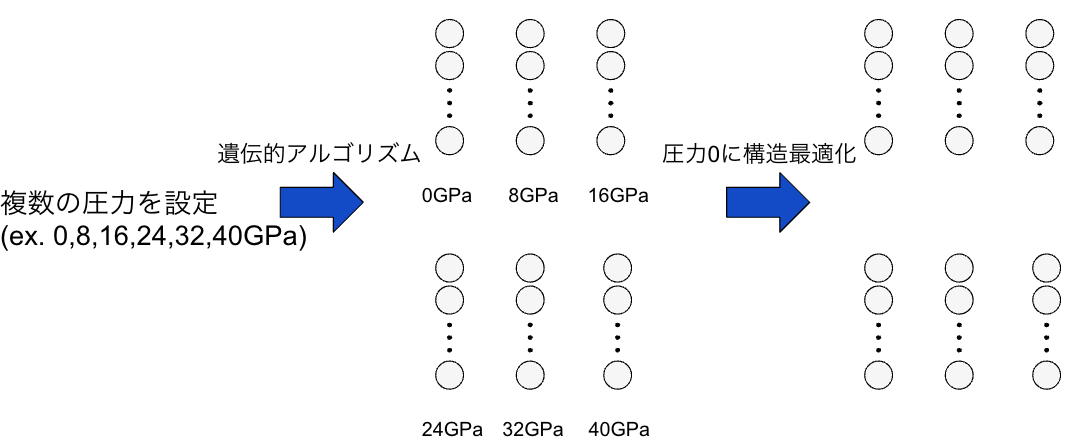
図7. 複数の固定した圧力で計算するアルゴリズム
実証:
“世代毎に圧力を変化させる” 方法および“複数の固定した圧力で計算する”方法,および圧力を0に固定する方法,高い圧力に固定する方法を比較しました.評価対象はMaterials Projectのデータベースですが,現実に存在する構造なので,周囲の圧力は1気圧=10-7 eV/A3であり,結晶にとっての単位系ではほぼ0です.
それぞれの方法で,6回の遺伝的アルゴリズムを回し,再現率とPFPを呼び出した回数をプロットすると図8,最終的な再現率は表2のようになりました.まず,現実に近いP=0の設定よりも高圧に設定したP=40GPaのほうが再現率が高くなりました.これにより,現実の準安定構造は高密度なものが多く,圧力をあえて高く設定したほうが再現率が高くなることがわかります.また,固定の圧力で計算するよりも, ”世代毎に圧力をランダムに変化させる”手法と,”複数の固定した圧力で計算する”手法のほうが再現率が高くなりました. 圧力の変化のさせ方による性能差は微々たるものでしたが,様々な密度の構造を探索するのが有効であることがわかりました.
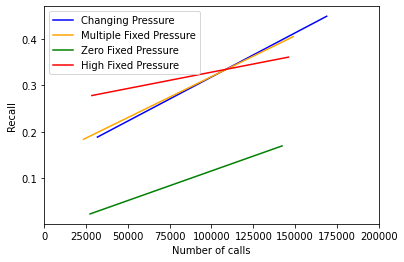
図8. 各圧力変化アルゴリズムでのPFPのコール回数(エネルギー計算回数)に対する再現率の増加.複数回実行し平均的な回帰直線をプロットした.
表2. 各アルゴリズムによる10世代後の再現率. それぞれ5回実行し,その平均と標準偏差を計算した.
| 手法 | 再現率 |
| 世代毎に圧力をランダムに変化 × 6 trials | 0.400 ± 0.015 |
| 圧力を固定 P = 0,8,16,24,32,40GPa | 0.378 ± 0.068 |
| 圧力を固定 P = 0 × 6 trials | 0.163 ± 0.060 |
| 圧力を固定 P = 40GPa × 6 trials | 0.341 ± 0.015 |
提案手法2: アニーリングによる不安定な構造の除去
手法:
次に,適合率を高める手法を考えました.探索で見つかった構造の中で,データベースにない構造の特徴を観察した結果,すぐに崩れてしまいそうな不安定な構造が多いことがわかりました.そこで,図9のように,遺伝的アルゴリズムで得られる候補にアニーリング操作を適用し,すぐに他の構造に変化してしまう不安定な構造を取り除き,適合率を高めることを考えました.
まず,結晶の構造に微小摂動を加え,変化した構造のエネルギーを計算し,エネルギーの上昇幅に応じた確率で変化させた構造に遷移させます. エネルギーの上昇量が小さいほど遷移させる確率が高くなるよう設定します.今回,この確率の設定には仮想的な温度によるボルツマン分布を仮定したメトロポリス法を用いました.また,仮想的な温度として室温300Kを設定しました.摂動を何度か繰り返した後,構造最適化を行い,元々の構造に戻ってこれなかった場合,不安定とみなし,取り除きます.
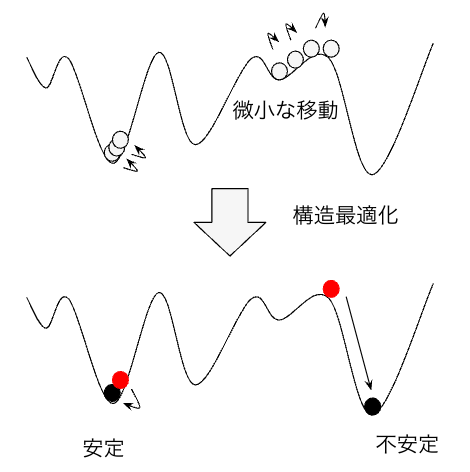
図9. 不安定な構造を取り除く手法
実証:
圧力を変えながら実験し得られた上位110個の構造のうち,原子間距離が近すぎない構造に対して,不安定な構造の除去を行うと図10が得られました. 左のグラフによると, 再現率は変わらない,すなわち,見つけられる構造の数は変わらないことがわかり,中央のグラフによると,精度は上がっていることがわかります. つまり,不安定な構造のみを切り落とし,実在する構造は残すことに成功しています.
また,右のグラフでみるように,得られた構造のうちエネルギーが小さい上位10個の構造の適合率のみをみると,大きく改善していることがわかります.
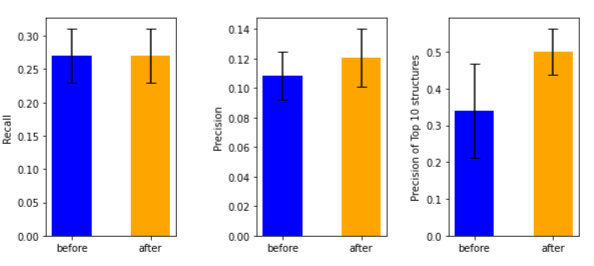
図10. 不安定な構造を取り除く前(before)と後(after)の再現率と適合率.(左) 上位110個の再現率,(中央)上位110個の適合率,(右)上位10個の構造の適合率
まとめ
結晶構造予測手法は従来から研究されていましたが,DFTを使用していることにより計算時間がとてもかかるものでした.
そんな中,今回の研究では,実現可能な結晶構造を探索する性能を測る指標と,指標を良くするアルゴリズムを考案しました. 炭素原子からなる結晶構造予測に手法を適用し,有効であることを実証しました. これらの手法は,PFPの予測の速さを活かし,実在する構造の発見率を高めるとともに,後々のDFTや実験などでの検証を効率的に行えるようにするものです.今後,NNPのような高速なエネルギー予測手法と結晶構造予測の組み合わせは,その実用性の高さからより発展していくと考えられます. そんな中で,今回開発した手法は効率性を高める汎用な手法として有用であると期待しています.
また,今回扱えなかったこととして,他の元素や複数元素系で同様なことが言えるか,エネルギー評価において温度を考慮する(自由エネルギーを扱う)とどうなるかなどが挙げられます. 温度を考慮する場合は,エントロピーの計算が必要となり,複雑な問題になりますが,近年温度を考慮する結晶構造予測についても研究が進んでいます. これらの手法を今回開発した効率化手法と組み合わせることにより,より現実的な結晶構造予測を行うことができると考えられます.
終わりに
今回,自分の研究の経験が浅いこともあって,自分の考えが発散してしまったり,何をすれば良いか分からなくなってしまうことがありましたが,毎日,メンターのお二方に相談させていただくことで,研究を進めることができました.
また,物性分野の知識が全くない状態からこの研究を行ったため,分からないことが多くありました. 分からないことを,メンターの方だけでなく,同じチームの方々,インターン同期の方々に質問させていただいたのですが,その際に,とても丁寧に教えていただきました. 発表の際に様々な分野の方々から,ご意見を頂いたのも大変参考になりました.お世話になった皆様に心より感謝申し上げます.
参考文献
[1] Oganov, Artem R., and Colin W. Glass. “Crystal structure prediction using ab initio evolutionary techniques: Principles and applications.” The Journal of chemical physics 124.24 (2006): 244704.
[2] Vilhelmsen, L. B., and Hammer, B. “Systematic study of Au 6 to Au 12 gold clusters on MgO (100) F centers using density-functional theory.” Physical review letters 108.12 (2012): 126101.
[3] Hong,C., et al. “Training machine-learning potentials for crystal structure prediction using disordered structures.” Physical Review B 102.22 (2020): 224104.
[4] Takamoto, S., et al. Towards universal neural network potential for material discovery applicable to arbitrary combination of 45 elements. Nat Commun 13, 2991 (2022).
[5] Jain, A., et al. “Commentary: The Materials Project: A materials genome approach to accelerating materials innovation.” APL materials 1.1 (2013): 011002.
[6] Mario V., and Oganov, Artem R. “Crystal fingerprint space–a novel paradigm for studying crystal-structure sets.” Acta Crystallographica Section A: Foundations of Crystallography 66.5 (2010): 507-517.