Blog
本記事は、2023年夏季インターンシッププログラムで勤務された玉置弦さんによる寄稿です。
はじめに
2023年度夏季インターンシップに参加した大阪大学大学院理学研究科の玉置弦と申します. 今回のインターンシップでは,Matlantis(https://matlantis.com/ja/)で提供されているニューラルネットワークポテンシャル(Neural Network Potential, NNP)であるPreFerred Potential (PFP)[1]、ブラックボックス最適化ソフトウェアOptuna、そしてPFNが保有するスーパーコンピュータMN-2を用いて、粉末試料に対するX線回折法(X-ray Diffraction, XRD)によるデータから結晶構造を高速に予測する手法開発を行いました。我々の提案法は従来手法に比べて最大400倍程度高速で、かつ専門知識を必要としない手法だけで従来手法のほぼ同等まで高精度に構造を予測できることを示しました。このブログでは、我々がどのようにしてXRDスペクトルデータを用いて結晶構造を予測しているかについてご紹介します。
背景
X線結晶構造解析とは
新規材料開発として特定の組成やプロセスで材料を合成した際、どのような結晶構造であるか、もしくは意図した結晶構造がうまく合成できているかを確認したい場合があります。X線結晶構造解析は、原子構造や分子構造を決定するために用いられ、結晶相や格子定数、粒径の決定など、その応用範囲は多岐に渡ります。その中でも粉末X線回折法は、測定装置も市場に普及しており、取り扱いも比較的容易であるため、結晶構造を調べる際の最初の分析手法といえます。粉末X線回折により得られたスペクトル(ここでは以降XRDスペクトルと呼びます)を用いて、結晶構造を解析することは従来から行われてきました。
従来のX線結晶構造解析分析手法
XRDスペクトルから結晶構造を決めるには、大きく2つの段階があり、大まかな結晶構造を決める段階(1段階目)と原子位置や格子定数を高精度に決める段階(2段階目)があります。これまで、1段階目ではデータベースを利用した探索が行われ、2段階目ではリートベルト解析と呼ばれる解析が行われてきました。
データベースを利用した探索は非常に単純で、与えられたXRDスペクトルに対してデータベースの中から類似したXRDスペクトルを持つ構造を検索し、それを求めたい大まかな結晶構造とするものです。
リートベルト解析では、候補となる結晶構造のXRDスペクトルをシミュレートし、実験結果に基づいてフィッティングを行います。パラメータには、格子定数や原子位置などの結晶構造に関するものとバックグラウンドノイズや装置関数の外部パラメータを含めて数十から百個程度の自由度が存在し、専門家による解析が必要となるほど複雑なものです。これらのパラメータをブラックボックス最適化の技術を利用して自動で探索する、自動リートベルト解析が近年開発されました[2]。しかし、リートベルト解析の探索結果は用いる初期構造に大きく影響され、またデータベースに類似構造が存在しない場合は探索が困難となるなどの問題を抱えていました。
データベースを用いないで結晶構造を予測する手法
そこで近年、データベースに依存せず結晶構造を予測する方法が開発されました[3]。遺伝的アルゴリズム・ベイズ最適化・リートベルト解析を用いて、与えられたターゲットに一致するXRDスペクトルを持つ結晶構造を予測することができます。
この手法の第一段階は遺伝的アルゴリズムに基づく大まかな結晶構造の決定です。遺伝的アルゴリズムによって候補結晶構造を生成し、これを密度汎関数理論(Density Functional Theory, DFT)に基づく第一原理計算によって局所的に安定な構造に最適化する、ということを逐次的に繰り返して”良い”構造を目指して探索を行います。DFT計算に基づく局所最適化は候補構造ごとに長大な時間がかかり、大まかに言って1000構造程度の評価に1日程度の時間がかかります。
手法の第二段階では、第一段階で得られたターゲットXRDスペクトルに近い候補構造に対して、ベイズ最適化に基づくある種の補間を行うことで、候補構造をより精密化します。この段階を踏むことで、続く第三段階のリートベルト解析の精度が向上することが報告されています。第三段階は従来のデータベースを用いた手法の最後の段階と同じくリートベルト解析です。候補構造を驚くほど精密化することができますが、その解析には専門的な知識を必要とします。
この手法は高い精度で与えられたXRDスペクトルに対する結晶構造を探索できる頑健な手法ですが、探索前に各元素の原子数を固定している点に拡張の余地があり、また構造の局所最適化に第一原理計算を用いている点に高速化の余地があります。
問題の定式化とコスト関数の設計
X線結晶構造解析は、ブラックボックス最適化問題と呼ばれる関数形が陽には分からない目的関数の最小化問題として定式化されます。X線結晶構造解析においては、与えられたXRDスペクトルに対して、それとなるべく近いXRDスペクトルを持つ結晶構造を求めたいわけですが、これは結晶構造を入力とし、与えられたXRDスペクトルに対するその結晶構造のXRDスペクトルの”距離”を最小化する問題として定式化されます。そのような距離を定めるものがコスト関数であり、コスト関数の設計はX線結晶構造解析の重要な要素の一つです。ブラックボックス最適化問題を解くための手法にはいくつかのバリエーションがありますが、概ね以下のような逐次的なやり方が用いられます。
- 探索点(ここでは候補となる結晶構造)を一つ選ぶ。
- その探索点の評価値(ここでは候補構造のXRDスペクトルをシミュレーションし、それとターゲットXRDスペクトルデータとのコスト関数の値)を計算する。
候補構造は後述する遺伝的アルゴリズムによって選ばれます。また、選択した候補構造に対するXRDスペクトルのシミュレーションは、pymatgen(https://pymatgen.org/) と呼ばれるライブラリを用いて実行することができます。ターゲットXRDスペクトルがどのような形式で与えられるかは実験の測定条件等に依存しますが、ここでは入射角0°から180°を等分割して得られた18000次元の実ベクトルとして扱います。pymatgenの`pymatgen.analysis.diffraction.XRD.XRDCalculator`を用いると、候補構造に対するXRDスペクトルを様々な条件を指定して生成できます。
コスト関数にも様々なバリエーションがあります。ここではX線結晶構造解析でよく用いられる負のコサイン類似度[4]およびR因子[5]について簡単に説明します。負のコサイン類似度とはコサイン類似度と呼ばれる二つのベクトル間の類似性を測る指標にマイナスをつけた量です。ターゲットXRDスペクトルと候補構造のXRDスペクトルはともに同じ次元の実ベクトルであるため、これを利用して候補構造のターゲットXRDスペクトルに対するコストを定義することができます。負のコサイン類似度の定義を以下に示します。ただし、\(\boldsymbol{x}\)を候補構造のXRDスペクトル、\(\boldsymbol{y}\)をターゲットXRDスペクトルとします。
\(-S_{\mathrm{cos}}(\boldsymbol{x}, \boldsymbol{y}) = -\boldsymbol{x} \cdot \boldsymbol{y} / (\| \boldsymbol{x} \| \| \boldsymbol{y} \|) \)
R因子とは、X線結晶構造解析の最終段階であるリートベルト解析においてよく用いられる指標であり、候補構造のXRDスペクトルとターゲットXRDスペクトルの間のユークリッド距離を適当な重みのもとで取った量です。R因子は以下で定義されます。ただし、\(\boldsymbol{x}\)を候補構造のXRDスペクトル、\(\boldsymbol{y}\)をターゲットXRDスペクトル、\(\boldsymbol{w}\)を重みベクトルとします。
\(R_{\mathrm{wp}}(\boldsymbol{x}, \boldsymbol{y}) = \sqrt{\frac{\sum_i \boldsymbol{w}_i (\boldsymbol{x}_i – \boldsymbol{y}_i)^2 }{\sum_i \boldsymbol{w}_i \boldsymbol{y}_i^2}}\)
\(\boldsymbol{w}\)は、\(\epsilon\)を小さな正の定数として\( \boldsymbol{w}_i = 1/(\boldsymbol{y}_i + \epsilon)\)と設定します。
候補構造とターゲットXRDスペクトルに対して上記のコスト関数を直接計算すると、候補構造のXRDスペクトルに対して不安定な関数となってしまう(=候補構造が少し変わると関数値が全く変わってしまう)ことが知られています。コスト関数の安定性を向上させるためには、XRDスペクトルを規格化することや、XRDスペクトルを適当な正規分布で畳み込みにかけて滑らかにすること、また構造の単位格子の体積を微小に変化させてコスト関数値をいくつか計算しそれらの最小値をとること、などの工夫が用いられます。
NNPの発展
計算機上で結晶構造パラメータを調整してエネルギー的に安定な構造に変化させることを構造緩和と呼びます。構造緩和はX線結晶構造解析に限らず、計算化学分野では広く用いられてきた手法です。しかし、従来用いられてきた第一原理計算手法であるDFT計算は計算に非常に時間がかかるという問題点がありました。
DFT計算による構造緩和の時間を大幅に短縮することが期待される技術として、NNPがあります。Preferred Computational Chemistryが提供するMatlantisで用いられているニューラルネットワークポテンシャルであるPFPは、DFT計算と同等の精度でありつつ最大で10,000倍ほど高速で、かつ72元素に対応した汎用的なNNPです。
結晶構造予測における遺伝的アルゴリズム
結晶構造を予測する際の第一段階目の手法として、遺伝的アルゴリズムがよく用いられます[6]。遺伝的アルゴリズムは、ブラックボックス最適化問題を解くための手法の一つです。遺伝的アルゴリズムには様々なバリエーションが存在しますが、概ね以下の初期集団の生成と評価、選択、交叉と突然変異、そして生成された構造の評価といったステップからなります。
初期集団(第一世代)の生成とは、結晶構造探索においてはいくつかの構造(通常は事前に定めた集団数(population size)分の構造)をなんらかの手法で生成する処理を指します。初期集団の生成手法にはいくつかの種類があり、単純にランダムに格子内に原子を配置するものや、対称性をまず決めてそれに合わせて原子を配置するもの、また格子をいくつかの領域に分割して一つの部分格子にのみ原子をランダムに配置してそれをコピーするものなどがあります。生成の際は、全ての原子間距離が共有結合半径の和よりも大きくなるなどの制約を課し、これらが満たされるようなもののみを採用することで、現実的にはあり得ない破綻した構造が生成されることを防ぎます。
初期集団の評価とは、初期集団に含まれる各構造に対して、上述のDFT計算やNNPを用いて構造緩和させ、緩和後の構造に対してコスト関数の値を計算することを指します。
選択とは、一つ前の世代の情報から次の世代の集団を生成する際に用いる構造(親構造)をいくつか選ぶ処理を指します。一つ前の世代の情報とは、実際にコスト関数値が評価された一つ前の世代と、それらを生成する際に用いられた構造集団(親集団)を指します。選ぶ際の基準には様々なものが考えられ、単純にコスト関数値の良い順に選んだり、同一の組成を持つ構造に集中しないよう多様性を持たせる方法などが考えられます[4]。
交叉と突然変異とは、選んだ親集団から次の世代の構造(子構造)を生成する処理を指します。交叉は二つ(以上)の親を用いて一つの子を作る処理であり、突然変異とは一つの親を用いて一つの子を作る処理です。具体的な交叉および突然変異の処理には様々なバリエーションがありますが、本研究では既存手法[6]や既存ソフトウェアASE(https://wiki.fysik.dtu.dk/ase/) と同種のものを用います。
課題とゴール設定
構造緩和のために用いられていたDFT計算をPFPによる計算で置き換えることによって、計算時間を大幅に短縮することを目指します。また、候補となる構造の組成範囲を与えることで原子数を固定せずに探索を柔軟に行う拡張を行います。さらに、Preferred Networksが独自に開発する結晶構造探索ソフトウェアを利用し、遺伝的アルゴリズムに基づいた探索のみを行うことでリートベルト解析等を行った場合と比べても高精度のX線結晶構造解析が実現できることを示します。
提案手法
本研究での提案手法の全体像を図に示します。探索するターゲットの情報として組成範囲とXRDスペクトルを入力すると、入力パターンに類似したXRDスペクトルを示す結晶構造を探索し、結晶構造の同定を行ってくれます。探索においては、構造緩和のためにPFPを用い、候補構造の生成のために遺伝的アルゴリズムを用いています。
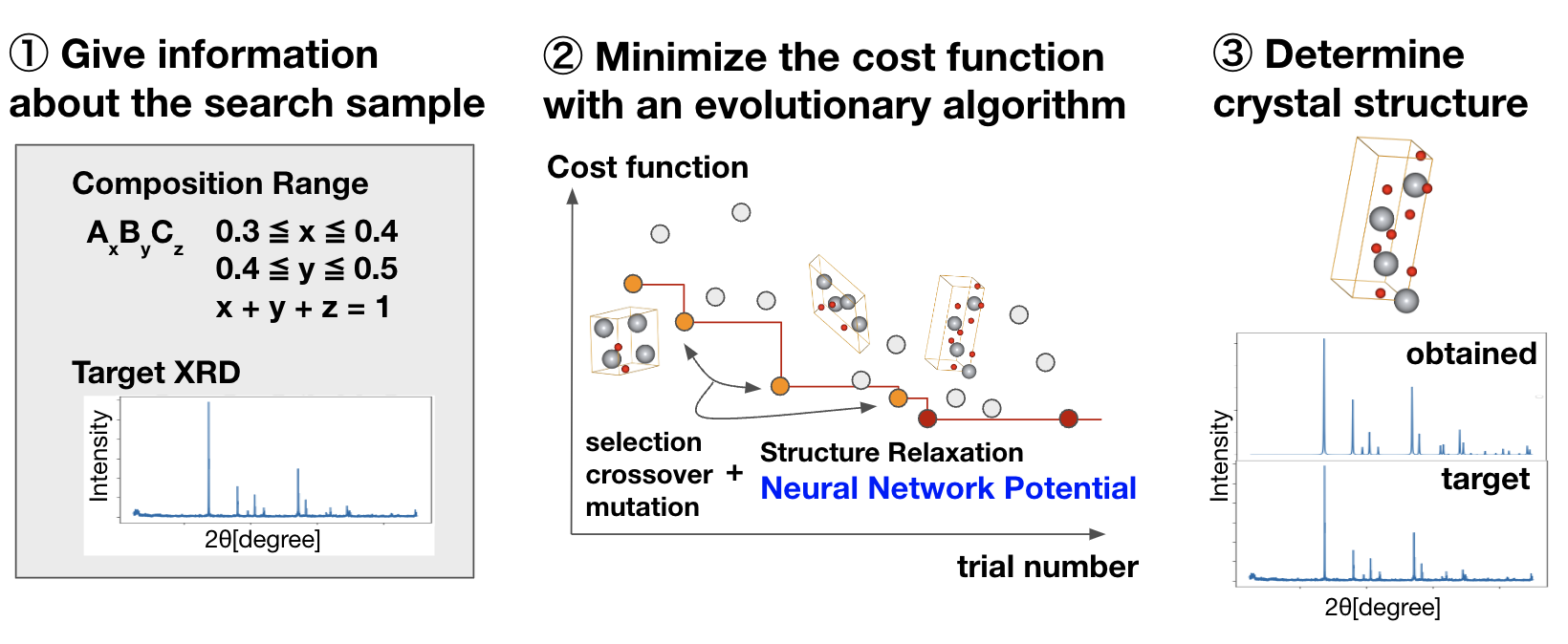
本研究の提案手法の全体像
構造緩和においてはPFPを用いて系に働く力をシミュレートし、L-BFGS[7]をベースに社内で独自に実装した最適化手法を用いました。候補構造を生成する遺伝的アルゴリズムについては、社内で独自に実装している結晶構造探索ソフトウェアのベースにしつつ、コスト関数などの実装を追加しました。コスト関数としては上述した負のコサイン類似度およびR因子を用いました。先行研究で負のコサイン類似度に対して行われていたように、コスト関数の安定性を向上させる工夫として以下の処理を追加しました。
- ターゲットXRDスペクトルおよび候補構造のXRDスペクトルを両者の最大値が1になるようにそれぞれ規格化しました。
- ターゲットXRDスペクトルおよび候補構造のXRDスペクトルを、平均0、標準偏差0.5の正規分布の+/- 5 sigmaの外側を切り捨てた切断正規分布を用いて畳み込みにかけました。
- 候補構造の単位格子の体積を0.95倍から1.05倍まで0.001刻みに変化させてコスト関数値をいくつか計算しそれらの最小値をとりました。
また、厳密な組成の測定が難しい場合でも柔軟に探索が行えるように、組成範囲を受け取ってその範囲内でのみ構造を探索するインターフェースを追加しました。二元素系の探索ならばその一元素目の範囲を、三元素系の探索ならばその一元素目と二元素目の範囲を、という風に範囲を指定できるようにしました。アルゴリズムとしては、初期構造の生成の際には指定した組成範囲からのみサンプリングすることにし、遺伝的アルゴリズムの交叉と突然変異の際には指定した組成範囲外の構造が生成された場合は再生成を行うことにしています。
また、実験データに対する探索を行う際はターゲットXRDスペクトルに対してバックグラウンドノイズを除く処理を行いました。具体的には5次のChebyshev多項式を用いてバックグラウンドノイズにフィッティングを行ってノイズを推定し、これをXRDスペクトルから引くことでノイズを除去しました。
結果
シミュレーションデータによる探索
ノイズを含まないシミュレーションXRDスペクトルを入力として、正しい構造を予想できるかの検証を行いました。用いたデータセットは、先行研究[3]で用いられていた、2元系(6構造)と3元系(6構造)の結晶構造データです。検証方法は、データセットにある結晶構造データからXRDスペクトルをシミュレートし、そのパターンを入力として用いました。構造の正誤判定は、pymatgenで実装されているStructure Matcherによって行いました。
ここで、コスト関数は上述したものを用いました。以降、負のコサイン類似度もしくはR因子とは、コスト関数の安定化のための工夫を行って求めた値のことを指すこととします。
組成比を完全に固定して、コスト関数として負のコサイン類似度を用いた探索結果を表に示します。提案アルゴリズムの精度を検証するため、12構造に対して5回ずつ探索を行いました。各探索におけるベストなスコアを先行研究[3]と比べると遺伝的アルゴリズムによる第一段階の探索の結果においては、スコアが上昇していることが確認できます。続いて、探索において最も良いスコアの構造が正しい構造(=先行研究にて正解と判定された構造)であるかを判定した結果、12構造中9構造は5回の探索全てで正しい構造を予測できており、3構造は正しく構造を予測できていませんでした。
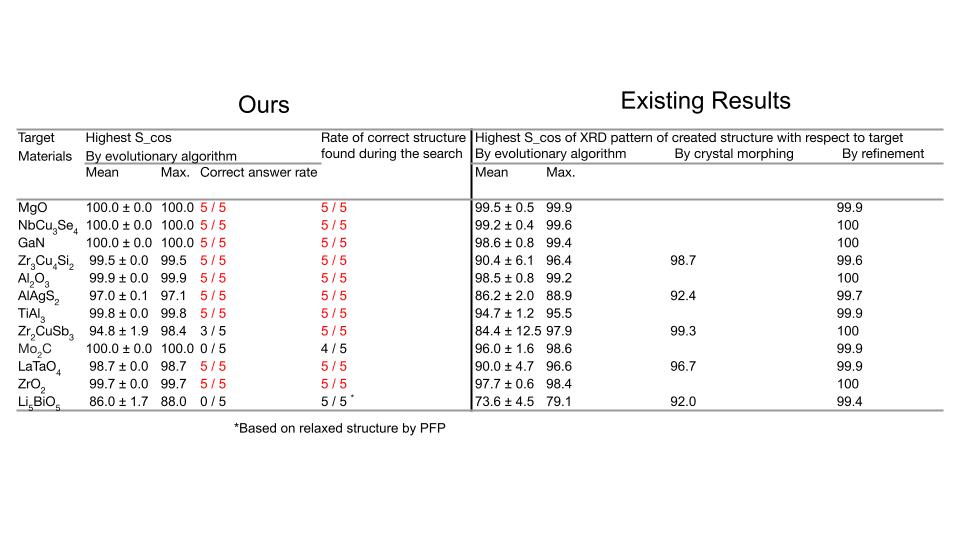
左表は組成比を完全に固定し、負のコサイン類似度で探索を行った結果。最大原子数=32、トライアル数=5000。右表は、先行研究[3]の結果。
正しく予測できていない原因を明らかにするため、正しく予測できていたMgOと予測できていなかったMo2Cに対して負のコサイン類似度の高い順から10構造について解析を行いました。正しく予測できていないMo2Cの場合、正解の構造よりも負のコサイン類似度及びR因子が良い値を取る構造が複数存在しました。XRDスペクトルを比較しても、非常に類似していることが確認できます。
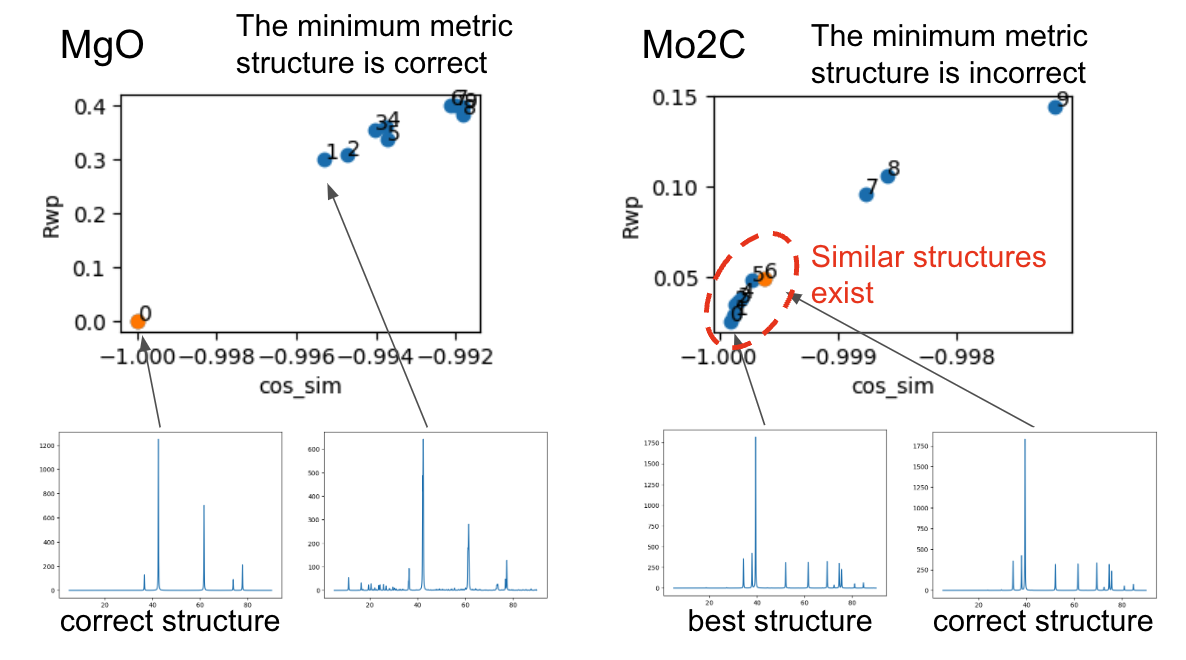
以上の解析により、最も良いスコアではありませんが、探索履歴の中には正しい構造が存在することがわかりました。探索履歴で正しい構造を見つけている割合は表の「Rate of correct structure found during the search」に記載されています。こうした探索の中で発見されている構造は、top-kの構造を可視化し人間の目で判断することにより発見される可能性があります。Li5BiO5については、入力構造であるDFT計算で緩和させた構造とNNPで緩和させた構造は異なる構造であると判定されました。本探索ではNNPによって構造緩和させた構造のみを出力するため、NNPで緩和させた構造との一致判定を行いました。大まかな結晶構造を予測することはできましたが、高精度に原子位置を予想することはできませんでした。
次に正しい構造を見つけるまでに要したトライアル(一つの構造の評価)数の平均と標準偏差並びに計算時間を評価しました。ターゲット構造によって、正しい構造を見つけるまでにかかるトライアル数は異なり、長くても平均的に1000トライアル程度で探索できていることがわかります。計算時間は10並列で1000トライアル計算を行うのに約1時間であり、DFTを用いる従来手法より10-30倍程度、ものによっては400倍程度高速であることがわかりました。
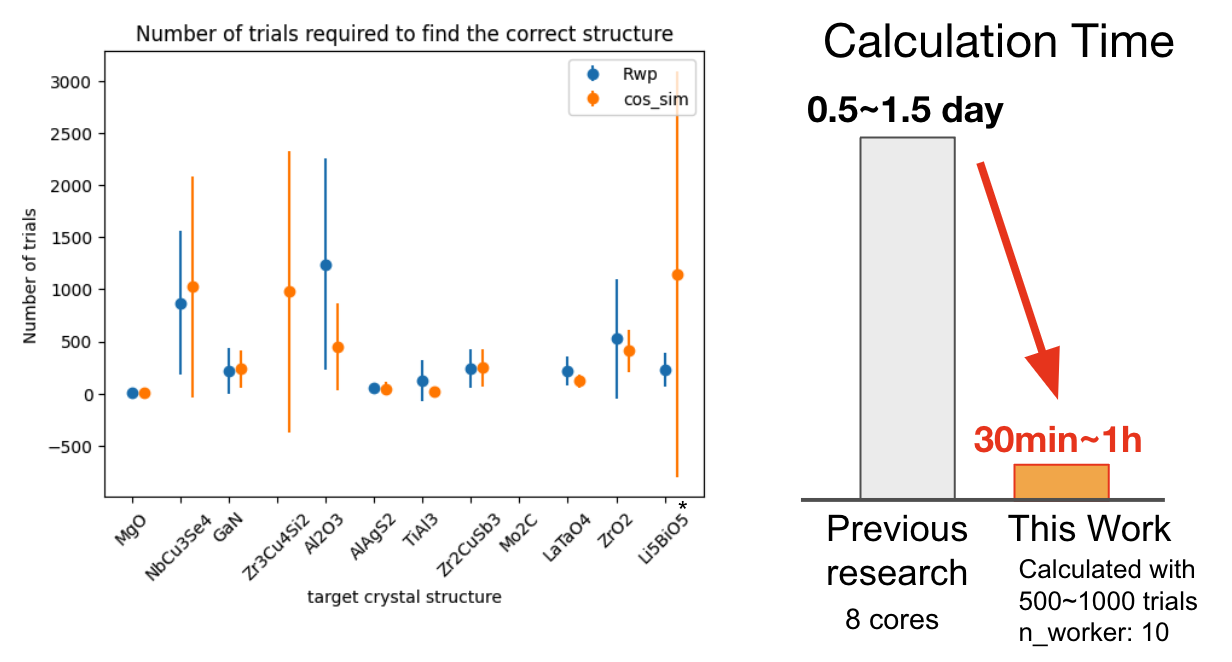
左図には正しい構造を見つけるまでにかかったトライアル数の平均と標準偏差、および右図には計算時間を示す。
実験データによる探索
提案手法がノイズなどを含む実験データにおいても正しい結晶構造を予測できるかを検証しました。用いたデータは、実験データベース RRUFF(https://rruff.info/)から、ルチル構造のTiO2、ブルカイト構造のTiO2, ペロブスカイト構造のCaTiO3、スピネル構造のMgAl2O4を選択しました。
まずは、組成範囲を全く限定せずに含まれている元素だけを与えて、負のコサイン類似度とR因子で探索を行いました。探索では、1世代当たり250個体として50,000個体(トライアル)の探索を行いました。その結果、ルチル構造のTiO2については正しい構造を見つけることができましたが、他の構造は正しい構造を見つけることができませんでした。構造の正誤判定は、Materials Project (https://materialsproject.org)に存在する同様の構造との比較を行いました。
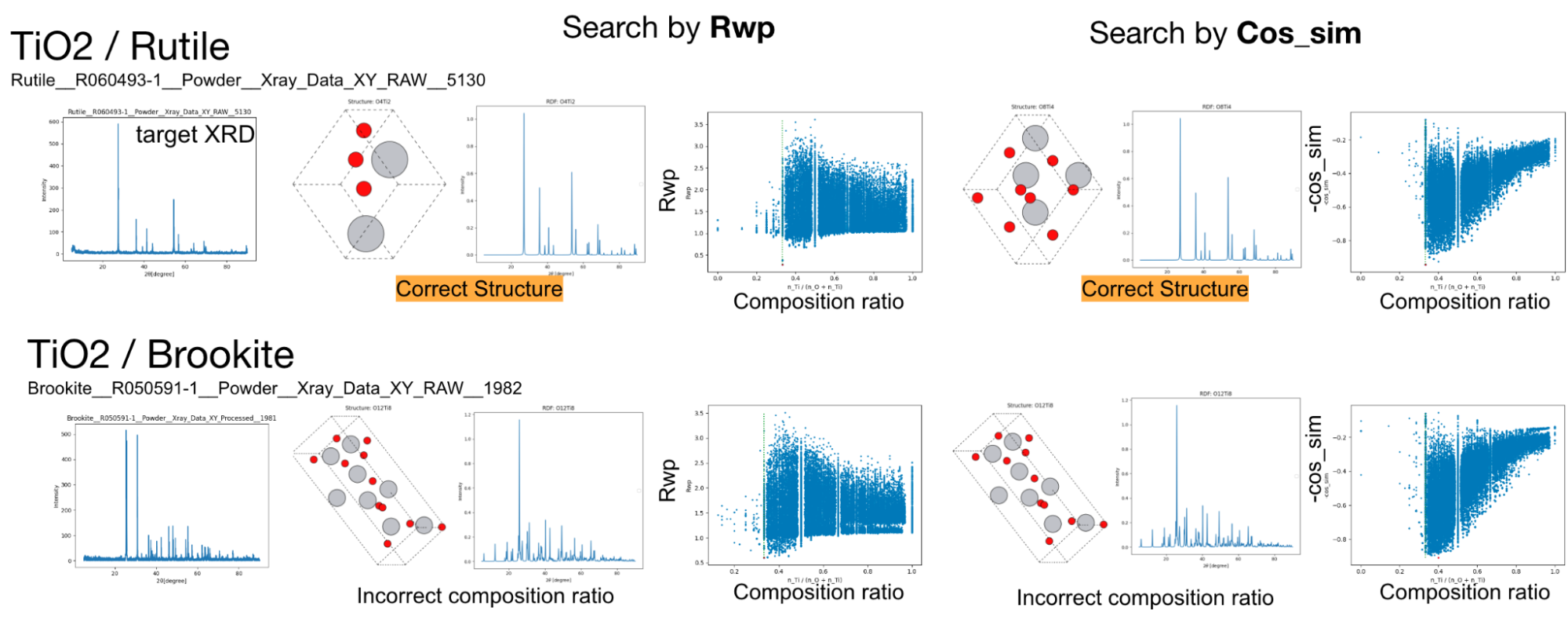
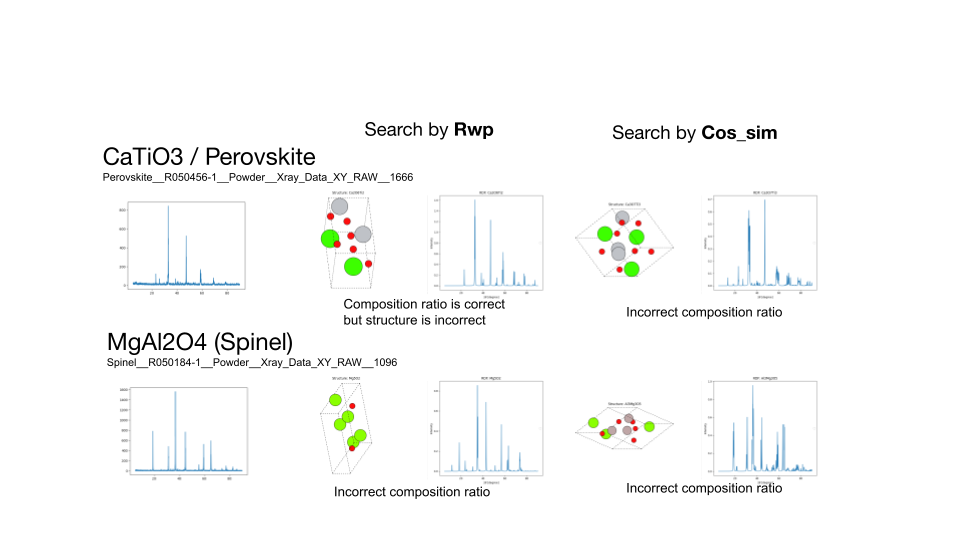
ルチル構造とブルカイト構造のTiO2の探索結果、およびペロブスカイト構造のCaTiO3、スピネル構造のMgAl2O4の組成を固定しない探索結果。左から順に、ターゲットのXRDスペクトル、R因子によって探索した結果、負のコサイン類似度によって探索した結果を示します。TiO2については、探索した組成比に対するコスト関数の値を合わせてプロットしています。
続いて、探索により見つからなかった原因を明らかにするため、組成範囲を限定して5000トライアルの探索を再度行いました。その結果、TiO2のルチル構造、ブルカイト構造とCaTiO3のペロブスカイト構造については正しい構造を見つけることができました。一方、MgAl2O4については見つけることができませんでした。この結果から組成範囲を全く限定しない場合では探索が十分に行えておらず、組成範囲を限定することで正しい構造を見つけることができたと考えられます。
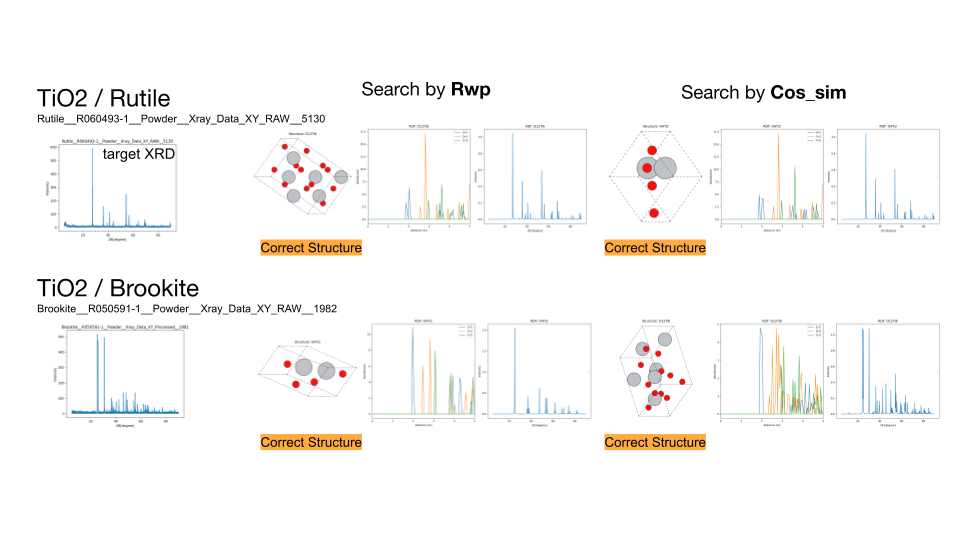
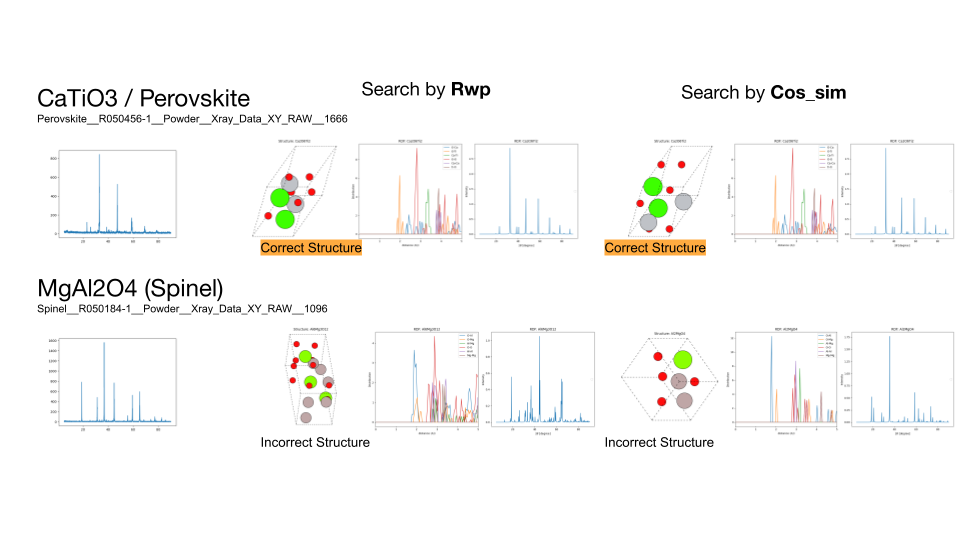
ルチル構造とブルカイト構造のTiO2の探索結果、およびペロブスカイト構造のCaTiO3、スピネル構造のMgAl2O4の組成を固定した探索結果。左から順に、ターゲットのXRDスペクトル、R因子によって探索した結果、負のコサイン類似度によって探索した結果を示します。各物質について見つかった構造とRDFプロット、XRDスペクトルを示す。
議論
本研究では負のコサイン類似度とR因子の両方をコスト関数として実験を行い、それらに対して安定化のための工夫をいくつか適用しました。しかし、探索の中では正しい構造を見つけられているが、コスト関数が最小のものが正しい構造でない状況がシミュレーションデータでも実験データでも起こっていました。したがって、XRDスペクトルの違いを定量化するコスト関数をさらに工夫する必要があると考えられます。
また、探索に用いるコスト関数と構造を決定するコスト関数を分けるアプローチが有効である可能性もあります。探索においては大まかな構造の正しさを判定するために正規分布による畳み込みをかける一方で、構造を決定する際はXRDスペクトルのピーク位置を精密に合わせるために畳み込みをかけないなどが考えられます。
また全く別のアプローチとしては、XRDスペクトルの類似度を計算する手続きを微分可能な形で記述し、勾配法で最適化するなどの改善策も考えられます。
おわりに
本研究ではX線結晶構造解析を行う手法をPFNが独自に開発する遺伝的アルゴリズムベースの結晶構造探索ソフトウェアの上に実装し様々な改善を行いました。PFPを用いることで最大400倍の高速化を実現し、また組成範囲を指定するインターフェースを実装することで柔軟な探索を実現しました。実現した手法は遺伝的アルゴリズムの探索のみで、シミュレーションデータで10/12、実験データで3/4の構造を発見することができ、高度な専門知識に基づくリートベルト解析を用いずに先行研究に匹敵する性能を達成することができます。
謝辞
研究テーマの設定から、日々のディスカッション、最終発表の準備まで多大なる貢献をいただきましたメンターの今村さん、柴山さんに心より感謝申し上げます。また、毎週の進捗報告会や最終報告会でアドバイスをいただきましたMaterial Scienceグループの方々にも感謝いたします。特に、実験の視点でのアドバイスは研究の方向性を考える上で重要な情報となりました。本研究では試行段階で多くの計算機資源を使わせていただきました。感謝いたします。お世話になりました皆様に心より感謝申し上げます。
[1] Takamoto, S., Shinagawa, C., Motoki, D. et al. Towards universal neural network potential for material discovery applicable to arbitrary combination of 45 elements. Nat. Commun. 13, 2991 (2022). https://doi.org/10.1038/s41467-022-30687-9
[2] Ozaki, Y., Suzuki, Y., Hawai, T. et al. Automated crystal structure analysis based on blackbox optimisation. npj Comput. Mater. 6, 75 (2020). https://doi.org/10.1038/s41524-020-0330-9
[3] Lee, J., Oba, J., Ohba, N. et al. Creation of crystal structure reproducing X-ray diffraction pattern without using database. npj Comput. Mater. 9, 135 (2023). https://doi.org/10.1038/s41524-023-01096-3
[4] https://en.wikipedia.org/wiki/Cosine_similarity
[5] Toby, B., R factors in Rietveld analysis: How good is good enough? Powder Diffraction, 21(1), 67-70 (2006). https://doi.org/10.1154/1.2179804
[6] Oganov A. R., Glass C. W., Crystal structure prediction using evolutionary algorithms: principles and applications. J. Chem. Phys., 124, 244704 (2006). https://doi.org/10.1063/1.2210932
[7] Liu, D. C.; Nocedal, J. “On the Limited Memory Method for Large Scale Optimization”. Mathematical Programming B 45 (3): 503–528. (1989). doi:10.1007/BF01589116.