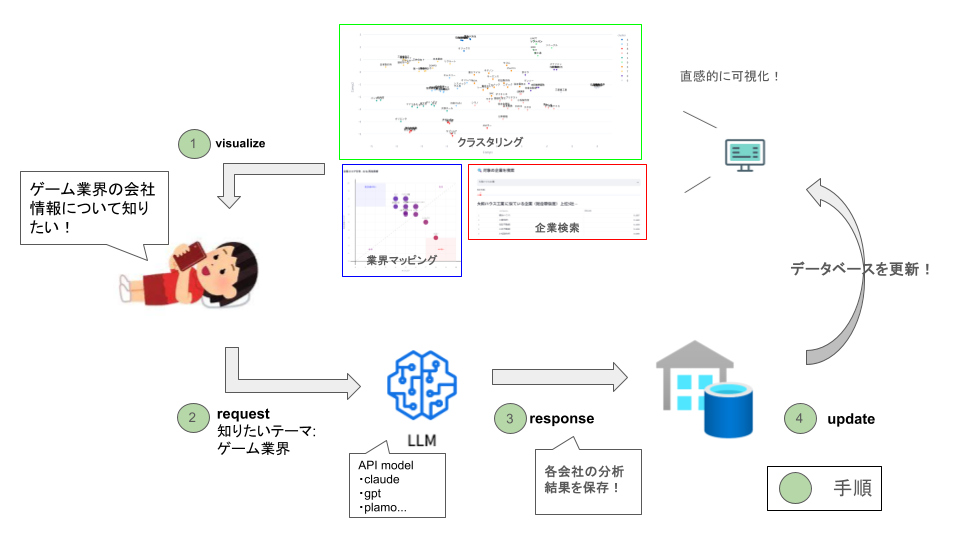
Blog
金融チームリサーチャーの平野(@_mhirano)です。深層学習を用いた数量ファイナンスを中心に研究に取り組んでいます。
私がインターン時代に取り組んでいたDeep Hedgingの研究に関して、人工知能学会金融情報学研究会(sig-fin)において、2022年度学生優秀論文賞を受賞しました。Deep Hedging (Buehler et al. 2019)とは、デリバティブを深層学習を用いて取引戦略を立ててヘッジする技術です。従来手法においては、この学習の際に、特定の価格シミュレーターを利用しなければならず、シミュレーターの性能に大きく依存していました。受賞研究においては、このシミュレーターを使用することなく、Deep Hedgingを行うことができる技術を開発しました。
本記事では、その技術的なエッセンスを紹介したいと思います。
- 人工知能学会論文: 原資産価格過程不要な敵対的Deep Hedging
- より詳しい論文: Adversarial Deep Hedging: Learning to Hedge without Price Process Modeling (ICAIF2023に採録決定済み)
本研究は、金融チームの南、今城との共著になります。
ヘッジ取引とDeep Hedging
ヘッジ取引とは、現在保有している資産等に対して、そのリスクを低減するような取引を行うことを指します。特に、デリバティブを中心に行われます。デリバティブとは、通常の金融商品から派生して作られた証券であり、原資産に連動してその価格が決まります。例えば、ヨーロピアン・コールオプションの場合、満期(定められた期間)の最終株価 \(S\) と、発行時に定められた行使価格 \(K\) に対して、 \(max(S-K, 0)\) の金額が支払われるようになっています。実際には、もっと複雑なオプションがあり、様々なリスクの低減のために使用されています。
一方で、これらのオプションを発行する証券会社は、販売に伴い、売りポジションを抱えることになり、このリスクをヘッジする必要が出てきます。本稿では、簡便化のため、株式を原資産としたヨーロピアン・コールオプションを、原資産でヘッジすることを考えることとします。このとき、証券会社は、満期に支払わないといけないであろう金額と確率を考慮に入れて、原資産の買い入れ量を決めていきます。しかし、株式価格が刻々と変わっていく中で、満期に支払わないといけないであろう金額の期待値も変化していくために、随時、原資産の買い入れ量を変化させていかなければいけません。これがヘッジ取引であり、人手でのヘッジは多大な人的コストがかかり、さばける量の限界や理論価格計算の難しさがあるため、この自動化・効率化が重要なのです。
この自動化にあたり、人間の代わりに深層学習で問題解決を行おうと考えたのが、Deep Hedging (Buehler et al. 2019)です。市場の情報を入力に取り、現時点で最適なヘッジを計算するニューラルネットで人間を置き換えてしまおうという取り組みを通じて、デリバティブ研究に変化を起こしつつ有ります。

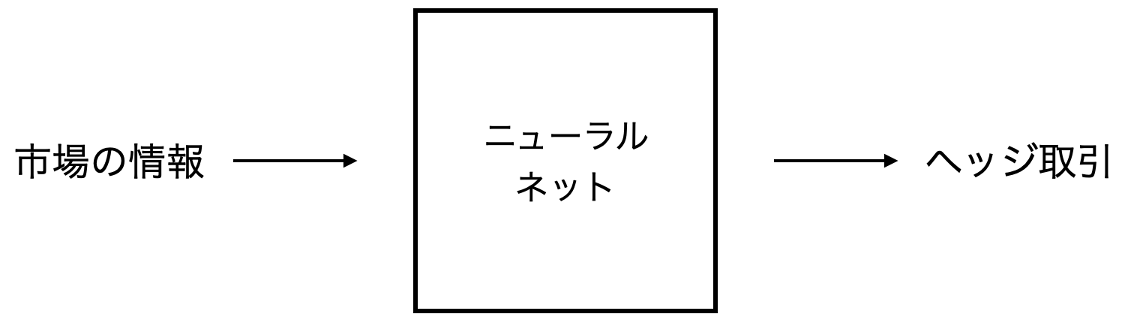
(図) 人間が市場の情報をもとにヘッジを行うケースとそれをニューラルネットで置き換えたケースの模式図
より詳細については、こちらの以前のtech blog もご参照ください。
Deep Hedgingと原資産のシミュレーション
前述の通り、Deep Hedgingは市場の情報を入力に取り、現時点で最適なヘッジを計算するニューラルネットによる構成されます。これを繰り返し満期まで行うことでヘッジを実施できます。
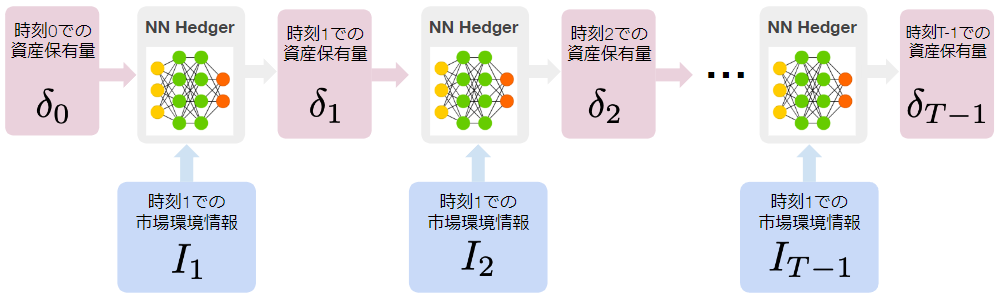
(図) Deep Hedgingが毎ステップ、ニューラルネットを用いてヘッジを繰り返す模式図
このニューラルネットの学習においては、特定の原資産価格系列を用いて計算がおこなわれていきます。このとき、最終的な損益(PL)は、次式のように計算できます。
\[\mathrm{PL}_T(Z,S,\delta) = -Z_T(S) + \sum_{t=0}^{T-1}(\delta_t(S_{t+1} – S_t) – c S_{t+1} \left|\delta_{t+1}-\delta_{t}\right|)\]\(Z_T(S)\)は、オプションの満期の支払い額、\(\delta_t\) は時刻 \(t\) における原資産保有量、\(S_t\) が時刻 \(t\) における原資産価格、\(c\) が取引コストの係数です。
そのうえで、リスク尺度関数 \(\rho\) (効用関数の符号を反転したもの)をもちいて、最適ヘッジ戦略は次の最小化問題として解かれます。
\[\min_\delta~\mathbb{E}\left[\rho(\mathrm{PL}(Z,S,\delta))\right]\]つまり、効用が最大になるようなヘッジの損益の最適化問題となります。
ここまでで、\(\delta_t\) は、ニューラルネットにより計算されますが、原資産価格 \(S_t\) は未知のものとなっています。では、この原資産価格をどのように設定していくか?ということについて考えていきます。
従来のDeep Hedging (Buehler et al. 2019) においては、この原資産価格は、ヘストンモデルやブラウン運動のような、これまでの金融市場の分析により獲得された、価格時系列をランダムに生成する数理モデルを採用していました。過去データには限りがあることと、過去データは最終的な性能評価に用いたいことを考慮に入れた場合に、学習において、数理モデルをもちいたシミュレーションの価格パスを用いることの有効性は高いといえます。また、シミュレーションを用いて学習した場合でも、充分に実データ上で性能を発揮できることもわかっています。
しかし、このシミュレーションによる価格パス生成において、どのようなモデルを用いるかについては、性能に対する影響が大きい一方で、正しい選び方が確立されていません。例えば、価格パス生成モデルにおいて、価格のジャンプを考慮に入れるかどうかでも性能が変わってくると考えることは自然でしょう。また、多くの数理モデルには、内部パラメータが存在しており、それをどのように決めていくかなどにも課題がある場合もあります。加えて、近年台頭している、深層学習による生成モデルなどに基づいた価格パス生成を採用するという候補もあります。
そこで、本研究では、原資産価格のモデルの仮定を行う必要がないDeep Hedgingの手法について提案しました。
敵対的Deep Hedging
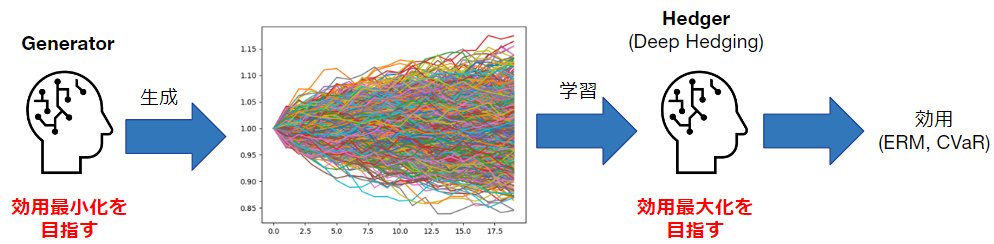
(図) 敵対的Deep Hedgingのコンセプト
敵対的Deep Hedgingとは、原資産価格の時系列自体も、モデルフリー的にニューラルネットワークで生成してしまう手法です。
ヘッジを担当するHedgerはこれまで通り、効用最大化を目指します。一方で、原資産価格を生成するGeneratorは、Hedgerの効用が最小になるように学習を行います。ニューラルネットワークを用いた勾配逆伝播法で学習を行う場合、GeneratorはHedgerを通じて、効用の勾配を獲得できるため、この勾配を用いて学習が可能です。
この敵対的な構造は、GAN (Goodfellow et al. 2014) や、Adversarial Learning/Example (Goodfellow et al. 2014) と似た構造で、この敵対的な構造ゆえによりよい解を得られる構造を持っています。今回の場合、GeneratorとHedgerはMin-Maxゲームとして定式化可能です。この敵対的学習の中では、Hedgerが、無リスクで利益を獲得できるケースがあればそれを学習する一方で、Generatorはそのような安易な利益を得られなくなるように学習する結果、実市場のように、簡単には利益を獲得できない価格時系列を得ることができると考えられます。
本研究の実験では、Generatorは、RNNベースのシンプルなものを、Hedgerは従来研究とほぼ同等のものを採用しました。
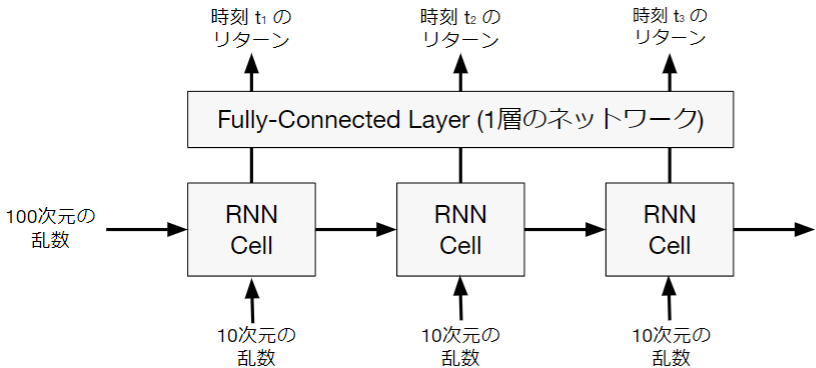
(図) 実験で採用したGenerator
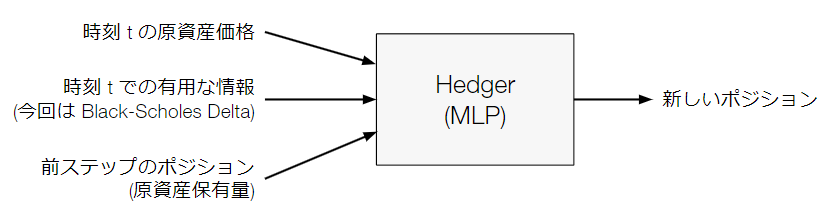
(図) 実験で採用したHedger
敵対的Deep Hedgingの性能評価
実際に上記の提案手法の性能を評価するために、実際に学習をおこない、実データを用いて評価を行いました。
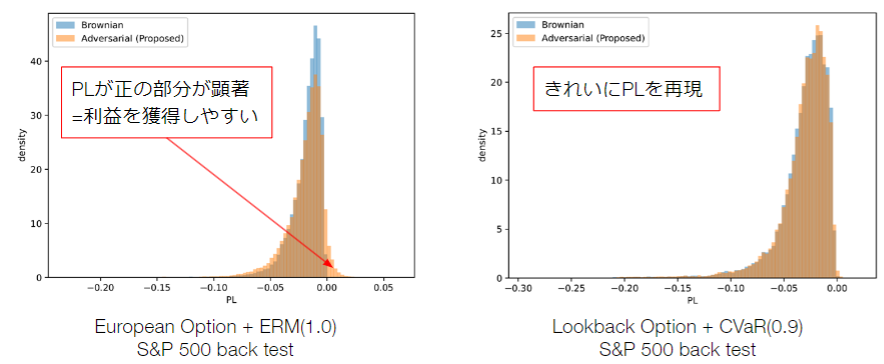
(図) 損益のプロット。オレンジが提案手法で、青が従来手法である。設定の異なる2種の結果を示す。
図はヘッジを通じた損益を表しており、ヘッジを通じてコストがかかるため、原則としてマイナスとなり、その期待値がオプションの価格となります。そのため、より損失の少ない分布の方がより良い結果と解釈できます。結果の図を見ていくと、どちらも従来手法とほぼ同じかより良い損益分布を獲得できていることがわかります。ここでは一部の結果しかお見せしていませんが、実験としてさまざまな環境で従来手法と比較を行ったところ、従来手法とほぼ同等の性能を達成していることが確認できました。
従来手法と同等の性能を達成できていることはかなり驚異的なことです。従来手法では、原資産の価格をモデル化し、それを入力として与えていました。しかしながら、提案手法では、その原資産価格のモデルさえも与えずに、無知識で学習を行わせています。そのため、原資産価格のモデル由来のバイアスも発生せず、かつ、煩雑なモデル化も不要となるにもかかわらず、これまでと同等の性能を発揮することは、驚異的であるといえるわけです。
なぜ、うまくいくのか?(簡易な理論解析)
ここまでを通じて、提案手法が実務的にうまくいくことは確認できました。ただ、これでは、なぜ、うまくいくのか?ということに対する答えが得られていません。そこで、最後に、簡易なケースを用いて、なぜ「無知識」でも、ヘッジを学べるかについて考察します。ここでは、数式をかなり抑えた説明をしますので、もし、数式的解釈のほうが好みであれば、論文(Adversarial Deep Hedging: Learning to Hedge without Price Process Modeling)を参照していただくことをお勧めします。
ここで、簡易的なケースとして、満期まで1ステップしかない状況を考えます。つまり、明日が満期として、ヨーロピアンコールオプションのショート(売りポジション)をヘッジするのに、どの程度原資産を買うか、というゲームを考えます。原資産価格とオプションの行使価格が一致している状況を考え、価格変動は、正規分布を仮定します。コールオプションを売っていますので、価格が上がれば満期の支払い(ペイオフ)が発生し、損失が発生します。一方で、価格が下がれば、満期の支払い(ペイオフ)が発生しませんので、満期での支払いが発生しません。非常に雑な計算をすれば、価格が上がる確率は、50%であるので、原資産は0.5単位購入しておけば大体良いわけです。原資産を0.5単位買っておけば、価格上昇時の損失は価格変動分の半分になり、価格下落時には、原資産の価値の減損に相当する価格変動分の0.5単位分になるため、上下での対称性をもった分布になり、価格上昇時にのみ損失が出るヘッジなしの状況よりも損益の分散を抑えることができます。
この簡易的なケースに対して、敵対的Deep Hedgingを考えます。Hedgerは、原資産を何単位(\(\delta\))買うのか、ということを考えます。一方で、Generatorは、価格変動の正規分布の平均(\(\mu\))と分散(\(\sigma\))をコントロール可能とします。
一度にすべてを動かしてしまうと現象理解がしにくくなってしまうので、まずはGeneratorを \(\mu=0\), \(\sigma=0.2\) に固定し、Hedger(\(\delta\))だけを動かしてみます。
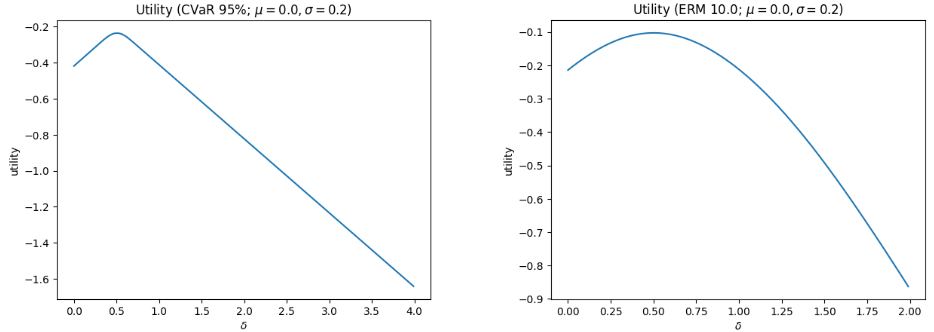
(図) Hedger(\(\delta\))のみを動かした場合のHedgerの効用
Hedger(\(\delta\))のみを動かした場合の結果の図をみると、\(\delta=0.5\) 付近に効用のピークがあることが確認できます。(厳密には、取引コストを考慮しているため、若干ずれます。)当初の想定通りの結果と言えます。
続いて、敵対的な環境として、Generatorの平均(\(\mu\))も動かしてみます。
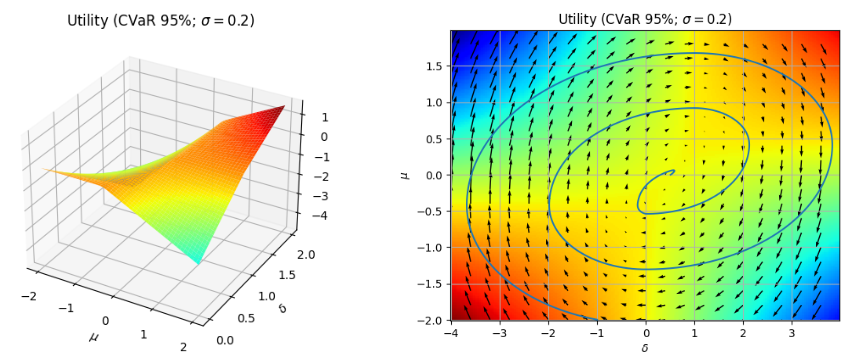
(図) Hedger(\(\delta\))とGeneratorの平均(\(\mu\))を動かした場合のHedgerの効用の一例。右の図内の青い線は、学習で収束していく状況のシミュレートを行った時のパラメータの遷移例。
敵対的な環境として、Hedger(\(\delta\))とGeneratorの平均(\(\mu\))を動かした場合、かなり複雑な挙動を見せます。右の図で見るのがわかりやすいのですが、横軸はGeneratorのパラメータ、縦軸がHedgerのパラメータとなります。Hedgerは効用が上がる方向に、Generatorは効用が下がる方向にパラメータを変化させようとする結果、学習においては、青い線のとおり、真ん中に収束していきます。この真ん中というのは、よく見ると、だいたい、\(\delta=0.5\)、\(\mu=0\) の付近になっています。つまり、敵対的な学習の結果として、Generatorは、価格変動の平均が0であるときが一番Hedgerに不利であることを学んでいます。
さて、ここで、実際の市場との対応を考えてみましょう。株式市場を考えるとして、一般に、企業の成長を考慮に入れない場合には、価格変動の期待値は、金利(ディスカウントレート)となります。今回の実験においては、このディスカウントレートを考慮に入れていないため、価格変動の期待値は0となり、上記の理論解析の結果と一致します。
さらにGeneratorの \(\sigma\) を動かしたケースはここでは割愛しますが、技術的にはまだ完全ではなく、ボラティリティーが大きくなるような価格生成をしやすいという課題も明らかになりました。詳しくは論文をご参照ください。
おわりに
本研究では、原資産価格過程を与えることなく、適切なヘッジ行動を学ぶことができる敵対的Deep Hedgingを提案しました。また、その機構の解析を通じて、この手法の有効性を解析し、技術的限界についても明らかにしました。
Deep Hedgingは、開拓され始めたばかりの分野であり、デリバティブヘッジにおいて、強力な力をもつとともに、可能性がまだあると考えられます。また、金融以外の分野への適用可能性もあると考えており、この技術を実社会に応用していきたいと考えております。