Blog
この記事はエンジニアの鈴木渓太の執筆です。
概要
- データ駆動でLLM Agentを開発するAutomated Design of Agentic Systems (ADAS) を提唱する論文の解説を行います
- 論文の手法をベースにした独自の手法により、高速且つ元論文を超える性能のAgentの開発に成功しました
- PFNでは引き続きLLM Agentの社会実装や研究開発を進めていきます
ADAS論文紹介
本段落ではAutomated Design of Agentic Systemという論文の解説を行います。この論文はLLM Agentの自動設計を提唱する論文であり、NeurIPS 2024 Open-World Agentic WorkshopのOutstanding Paperに選出されています。
論文URL: https://arxiv.org/abs/2408.08435
GitHub: https://github.com/ShengranHu/ADAS
はじめに
近年、Deep Research[1]やGitHub Copilot[2]に代表されるLLM Agentを活用したアプリケーションが急速に普及し、従来のチャットボットでは実現困難だった複雑なタスクの自動化が進んでいます。これらのLLM Agentシステムは、複数の役割を持つAgentが協調するなど、多様な要素で構成されるのが一般的です。現状では、こうしたAgentシステムの設計は人間の専門家が経験とドメイン知識に基づいて行っていますが、LLMに対する深い理解とタスク固有の知識が求められるため、容易ではありません。特に、今後タスクの複雑化やAgent構造の高度化が進むにつれ、より大規模で複雑なアーキテクチャの構築が必要となり、設計の難易度はさらに高まると考えられます。機械学習の歴史を振り返ると、画像認識分野においてHog/SIFT特徴量がCNN[3]に取って代わられたように、手作業で設計されたモデルが学習ベースのモデルに置き換わってきた事例が数多く見られます。この経験則に着想を得て、著者らはLLM Agentの設計そのものを学習によって自動化するフレームワークであるAutomated Design of Agentic Systems (ADAS) を提唱します。ADASの究極的な目的は、人間が設計するより高性能で、多様なタスクに対応できるAgentシステムを自動生成することです。著者らは、ADASが強力なAI Agent開発の最速の道筋になり得ると主張しており、実験では学習によって自動設計されたAgentが従来の手動設計を上回る性能を示すケースも確認されています。これは、開発効率の向上だけでなく、人間の開発者を凌駕する可能性を示唆しています。
提案手法: Meta Agent Search
ADASのフレームワークは、主に「探索空間」「探索アルゴリズム」「評価関数」という3つの主要素から成り立っています。進化計算[4]と同様に探索アルゴリズムが反復的に探索空間内から有望なAgent構成の候補を探索し、評価関数の最適化(最小化または最大化)を目指します。Agentはコードによって記述されるため、プログラミング言語のチューリング完全性に基づき、探索空間は原理的に「任意のエージェント構造」を包含します。論文では探索アルゴリズムとしてMeta Agent Searchを提案しています。Meta Agent SearchはLLMが過去の探索を通じて蓄積されたAgentの構造や、タスクに対する正解率といった評価関数の値を記録した履歴データを参照して新たな有望なAgent構成を生成する手法であり、Meta Agentには通常高性能なフロンティアモデルが使用されます。生成されたAgentは、特定のタスク群でその性能が評価され、当該Agentの構成と評価結果が履歴に追加されていきます。この一連のプロセスを繰り返すことにより、人間が明示的にプログラムしなかった複雑かつ効果的な設計パターン、例えば複数の思考連鎖の利用や高度なフィードバック機構などが、自律的に創発されることが確認されています。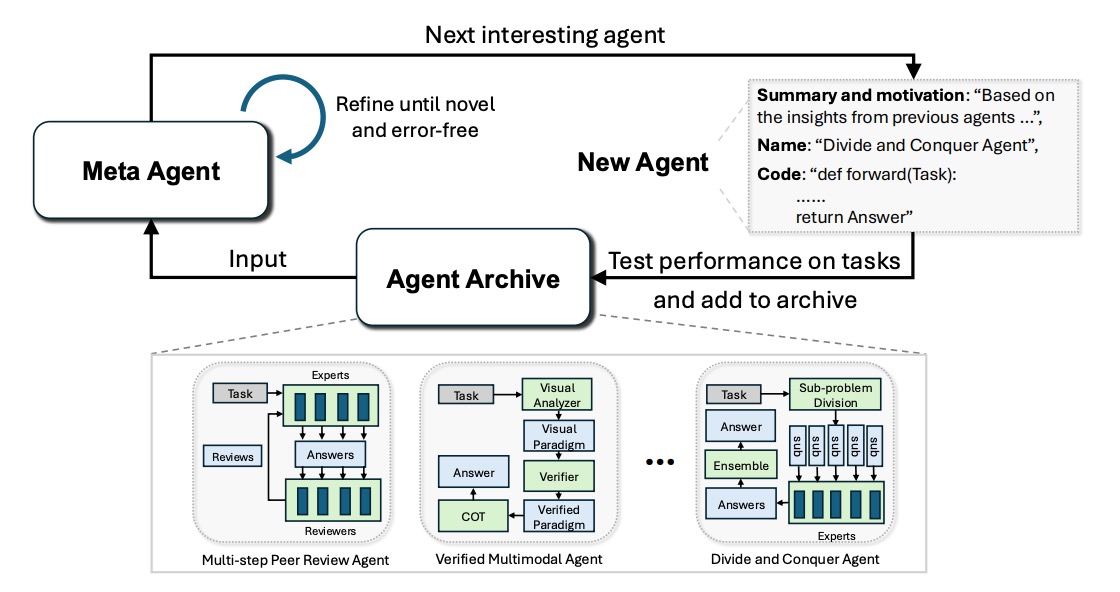
図1. Meta Agent Searchの模式図
実験
論文ではADASの提案手法であるMeta Agent Searchの有効性を示すためARC(Abstraction and Reasoning Corpus)[5]、 DROP[6]、MGSM[7]、 MMLU[8]、 GPQA[9]の5つのベンチマークについて実験を行っています。それぞれのベンチマークの説明は以下の通りです。
- ARC (Abstraction and Reasoning Corpus): 視覚的なパズルからルールを学習し適用する、汎用的な問題解決能力を評価
- DROP: 段落をまたがる複雑な読解と推論能力を評価
- MGSM: 多言語で記述された数学的問題解決能力を評価
- MMLU: 多様な学術分野にわたるマルチタスク問題解決能力を評価
- GPQA: 大学院レベルの難解な科学的問題解決能力を評価
比較用のベースライン手法としてはChain-of-Thought (COT)[10]、 Self-Consistency with COT (COT-SC)[11]、Self-Refine[12]、 LLM-Debate[13]、Quality-Diversity[14]、Step-back Abstraction[15]、Role Assignment[16]を用いています。Meta AgentにはGPT-4[17]を用い、コスト面を考慮してMeta Agent Searchの出力のAgentやベースラインの評価はGPT-3.5[18]を用いています。評価指標としてはDROPはF1スコアを用いて、それ以外のベンチマークは正解率を評価指標としています。それぞれのベンチマークをvalidationとtestに分割し、validationデータで最適化されたアーキテクチャのtestデータに対する評価値を計測します。DROP, MGSM. MMLU, GPQAの4つのベンチマークにおけるADASで作成されたAgent、ベースラインのAgent、そしてprompt最適化[19]を適用した場合の評価値を図2に示します。表からベースラインのAgent手法や、prompt最適化に比べて高いスコアを記録しているのが見て取れます。
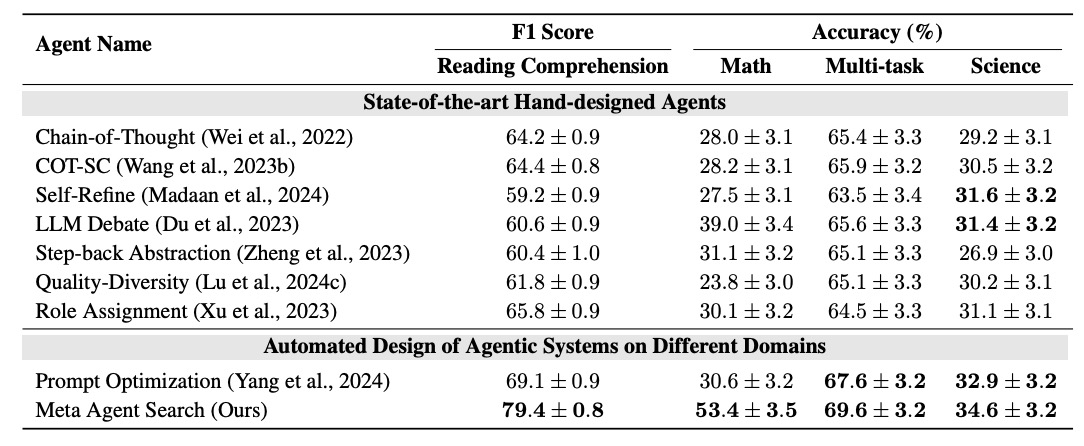
図2. DROP, MGSM, MMLU, GPQAのADASとベースライン、Prompt最適化のスコア
また、ARCについてはvalデータに対してiterationが進むほど、より優秀なAgentが発見されtestデータの正解率が高くなっていくのが観測されています (図3の左図)。最終的に発見された最良のAgent構成は図3の右図の通りです。
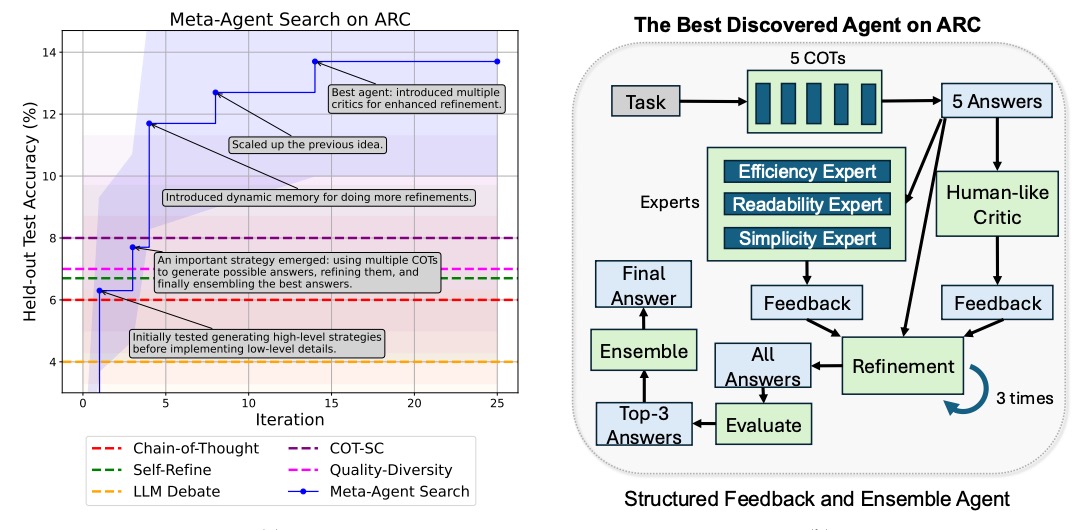
図3. Iterationごとに選択されたモデルのtestデータの正解率の推移と最終的に選択されたモデル
Meta Agent Searchによって発見されたアーキテクチャを分析した結果、それらが単なる既存手法の組み合わせに留まらず、新規性のある独自の構造を有していることが明らかになりました。例えば、GPQAベンチマークにおいては、複数の専門家モジュールと批評家モジュールが協調して査読と改善を繰り返す「Multi-Step Peer Review Agent」や、問題を部分問題に分割し各専門家が解決にあたる「Divide and Conquer Agent」といった、独創的かつ効果的なエージェントが提案されました。
得られたモデルの汎化性能の検証実験
特筆すべき点として、Meta Agent Searchによって発見されたAgent設計は、訓練時とは異なるドメインやLLMに対しても優れた汎化性能を示すことが確認されました。具体的には、MGSMで発見された高性能な上位3つのエージェントを選定し、同一数学ドメインのGSM8K[20](一般的な小学校レベルの数学問題)およびGSM-Hard[21](GSM8Kより難易度の高い数学問題)、さらに異種ドメインであるMMLUとDROPを用いて評価実験を行いました。図4に示す結果によると、同一数学ドメインのGSM8Kではベースライン比で25.9%、GSM-Hardでは13.2%の精度向上が認められました。これは、MGSMで発見されたAgent設計が、数学という広範なドメイン内で極めて効果的に機能することを示しています。さらに注目すべきは、これらの数学ドメインで発見されたAgentが、DROPやMMLUといった全く異なるドメインに適用された際にも有効性を維持した点です。これらの非数学ドメインにおいては、各ドメイン専用に設計されたAgentの性能には及ばないものの、ベースラインのAgentを上回る結果を示しました。この事実は、Meta Agent Searchが発見する設計パターンが、特定のドメインに特化した構成だけでなく、より汎用的な思考プロセスや問題解決戦略を獲得している可能性を示唆しています。
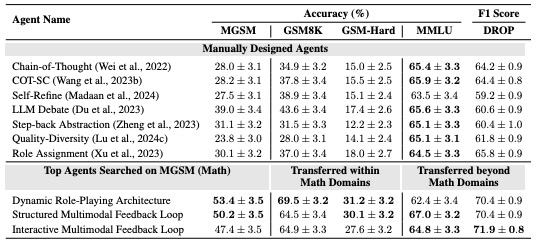
図4. MGSMで学習したAgentの他ベンチマークでの性能
さらに、発見されたAgent設計が特定のLLMの特性に過度に依存せず、異なるLLMでも機能するかという点についても検証が行われました。ARCベンチマークにおいて、GPT-3.5による評価でテスト精度が最も高かった上位3つのAgentを選び、Claude-Haiku[22]、GPT-4[23]、Claude 3.5 Sonnet[24]という3種類のLLMを用いて再度ARCでの評価を実施しました。その結果、図5に示すようにGPT-3.5を用いて探索されたAgentは、これら3つの異なるLLMに対しても有効に機能することが示されました。特に注目すべきは、評価に用いたモデルの中で最も高性能とされるClaude 3.5 Sonnetを使用した場合、最高性能のAgentがARCで約50%の精度を達成した点です。ARCが抽象的かつ高度な推論を要する難易度の高いベンチマークであることを考慮すると、この数値は非常に高い水準と言えます。この結果は、Meta Agent Searchによって発見されたアーキテクチャが、初期評価に用いたGPT-3.5のみならず、特性の異なる他のLLMにおいても効果を発揮することを示しており、発見されたアーキテクチャがモデル固有の特性に依存しない、汎用的な有効性を持つことを裏付けています。
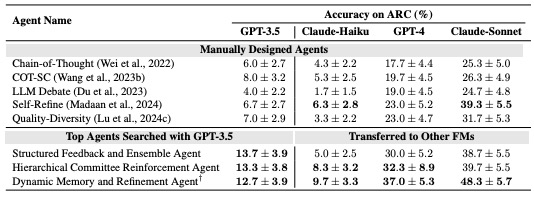
図5. GPT-3.5で学習したAgentの他モデルを用いた時のARCの性能
ADAS実用化に向けた検討
前段まではADASについてとその提案手法であるMeta Agent Searchの論文についての解説を行ってきました。以降ではLLM Agentの「複雑さ」の観点からADASの実運用に向けた検討を行います。
LLM Agentの複雑さが実運用に及ぼす影響
LLM Agentの複雑さは、実用上、ADASの探索効率とLLM Agent自身の推論速度という二つの側面に大きな影響を及ぼします。
ADASは、LLM Agentの集団から新たなAgentを生成し、集団を更新していく進化計算的なアプローチを採用しています。一般に、進化計算では探索空間が広大になると収束に時間を要し、実用的な時間内で最適解を得ることが困難になる場合があります[25]。この問題と同様に、ADASの文脈では複雑なアーキテクチャを持つAgentは高い潜在性能を持つ一方で、その複雑さ故に探索空間が広大になり特にリソースが限られている状況下では、最適なアーキテクチャの発見に至らない可能性があります。対照的に単純な構造のAgentは潜在性能こそ複雑なものに劣るものの、限られた計算リソースでも効率的に探索が進み有望な解に収束する可能性を秘めています。
LLM Agentの複雑さは、推論時の処理速度にも直接的な影響を与えます。Agentの推論時間はユーザーの待ち時間に繋がり、UXを大きく左右します。たとえAgentによって業務が自動化されても、処理時間が従来の業務時間を上回るようでは、その恩恵は薄れてしまいます。業務内容によっては、長時間の待機が許容されないケースも少なくありません。特に、ユーザーとの対話やリアルタイム応答が不可欠なアプリケーションにおいて、推論時間の最適化は実用化の必須条件と言えるでしょう。したがって、推論速度の観点から、Agentの複雑さを適切に制御することが実用上求められます。
これらの理由から、ADASを実用化する上でLLM Agentの複雑さを考慮することは極めて重要です。本稿では、実用化に向けたアプローチとして、LLM Agent内のLLMの推論の合計回数を固定することでAgentの複雑さを制御する手法を導入したMeta Agent Searchについて検討します。この手法を通じて、以下の観点を検証します。
限られた計算時間で高速且つ高性能なLLM Agentを構成することができるか?
ベンチマーク
本研究では、ベンチマークとしてOmni-Mathデータセット[26] を採用しました。このデータセットは、国際数学オリンピック(IMO)レベルの設問を含む4,428問から成り、代数や幾何学など33以上の数学分野と10段階以上の難易度で詳細に分類されています。これにより、モデルの数学的能力を多角的に評価することが可能です。Omni-Mathに収録されている問題の多くは、計算や定理の単純適用では解けません。解法には、問題の構造に対する深い洞察や非自明な定理の組み合わせが要求されます。したがって、このデータセットは、モデルが表面的なパターン学習に依存せず、知識を応用する汎化能力や、真の数学的推論能力を獲得しているかを測る上で極めて有効な指標となります。評価実験では、Omni-Mathの難易度指標(0.5から10.0、数値が大きいほど高難度)に基づき、難易度2.0~3.0の範囲から、解答が浮動小数点数(float)としてパースできる280問を抽出して使用しました。以下に、抽出された問題の一例を示します。この問題は、条件を満たす配置を単純に数え上げるだけでは重複が発生しやすく、問題設定を適切にモデル化し、重複を正確に排除する組合せ論的な思考力が求められます。
問題:
教室には5×5の配列で机が並んでおり、0人から25人までの生徒が座ります。生徒が机に座るための条件は、その机と同じ行にある他のすべての机が埋まっているか、または同じ列にある他のすべての机が埋まっている(あるいはその両方)ことです。どの生徒がどの机に座るかを区別せず、使用されている机の配置のみを考えた場合、可能な配置は何通りありますか?
実験: LLM Agentの最適な推論の合計回数の決定
手法
本実験では「限られた計算時間で高速且つ高性能なLLM Agentを構成することができるか? 」というテーマを検証するために、問題を解くAgentを生成するMeta Agentの指示に推論回数を指定する項目を追加します。具体的には、以下の様に生成するLLM Agentの推論回数の合計を特定の値(NUM_INFERENCEとしてパラメータ化し、本実験では後述する固定値群を順次適用)に制限するよう指示します。本稿では、この推論回数の固定を通じてLLM Agentの複雑さを制御することを試みます。この手法は、探索空間を意図的に低次元の部分空間に射影・限定する、従来の進化計算におけるテクニック[27]と類似しています。
# Important Constraint
– It is also possible to send multiple queries to an LLM Agent in a single step.
– When having an Agent perform multiple reasoning steps in a single stage, count each reasoning instance separately rather than counting it as a single reasoning step. For example, if 3 reasoning steps were performed in step 1, count it as 3 separate reasoning steps rather than just 1.
– Design “forward” function so that the total number to call LLM Agent is always exactly [NUM_INFERENCE] times. (Important)
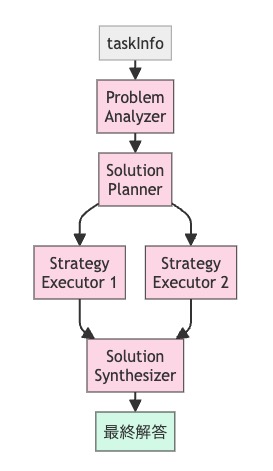
図6. 推論回数が5回のAgent例の模式図
例えば図6のAgent構成ではLLMの推論回数は5回であり、入力から出力までのフローを考えた時の中間ノードの数に対応します。実験では、推論回数の指定を1、2、3、4、5、7、9、11、13、15回という10段階に設定し、これらの各設定においてLLM Agentの最適化を行います。まず、350問から成るvalidationデータセットを用い、各推論回数設定に対して、前述の複雑さ制御を導入したADASを20iteration実行します。各設定について、この20iterationで得られたAgentのうち、validationデータセットに対する正解率が最も高かったものを、その推論回数設定における最良Agentとして選定します。最後に、こうして選定された各最良Agentに対し、350問から成るtestデータセットを用いて最終評価を行い、それぞれの正解率および1問あたりの平均実行時間を計測・集計します。
結果
以下に、本実験の結果を示すグラフおよび表を提示します。これらには、推論回数を指定したMeta Agent Searchによる結果に加え、比較対象となるベースライン手法の評価結果も含まれています。ベースラインとして採用した既存手法は、ADASの元論文でも用いられているChain-of-Thought (CoT)、Self-Consistency with CoT (CoT-SC)、Self-Refine、LLM-Debate、Step-back Abstraction、Quality Diversity、およびDynamic Assign of Rolesの7つです。これらの各Agentについて、validとtestデータにおける正解率と1問あたりの平均推論時間を示します。基本的には推論回数が多いほど一問あたりの平均推論時間は大きくなりますが、一回の推論における入出力トークン数によって多少前後することがあります。
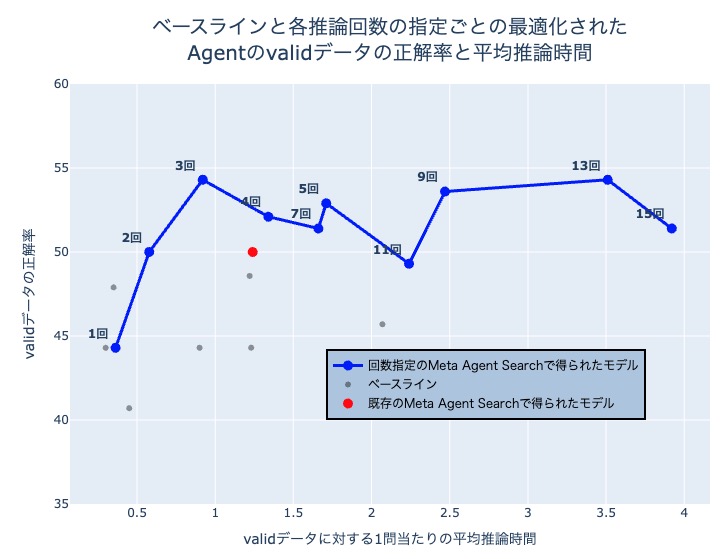
図7. ベースライン, 既存手法と各推論回数ごとに最適化されたAgentのvalidスコア
| Meta Agent Searchの制約 | validデータの正解率 (%) | 一問あたりの平均推論時間 (秒) |
| 1回推論 | 44.3 | 0.363 |
| 2回推論 | 50.0 | 0.578 |
| 3回推論 | 54.3 | 0.92 |
| 4回推論 | 52.1 | 1.34 |
| 5回推論 | 51.4 | 1.66 |
| 7回推論 | 52.9 | 1.71 |
| 9回推論 | 53.6 | 2.47 |
| 11回推論 | 53.6 | 3.47 |
| 13回推論 | 54.3 | 3.51 |
| 15回推論 | 51.4 | 3.92 |
| 回数制限なし(既存手法) | 50.0 | 1.24 |
表1. 既存手法と推論回数を固定して得られたAgentのvalidデータに対する正解率と1問当たりの平均推論時間
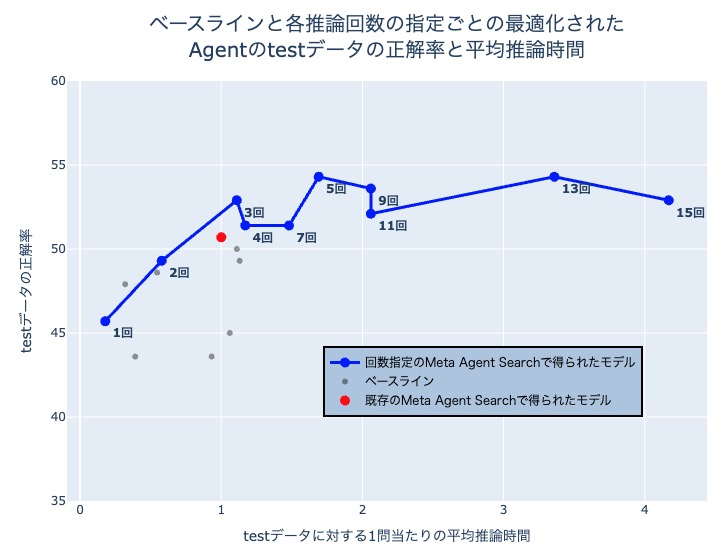 図8. ベースライン, 既存手法と各推論回数ごとに最適化されたAgentのtestスコア
図8. ベースライン, 既存手法と各推論回数ごとに最適化されたAgentのtestスコア
| Meta Agent Searchの制約 | テストデータの正解率 (%) | 一問あたりの平均推論時間 (秒) |
| 1回推論 | 42.1 | 0.166 |
| 2回推論 | 49.3 | 0.578 |
| 3回推論 | 52.9 | 1.11 |
| 4回推論 | 51.4 | 1.17 |
| 5回推論 | 54.3 | 1.69 |
| 7回推論 | 51.4 | 1.48 |
| 9回推論 | 53.6 | 2.12 |
| 11回推論 | 57.1 | 3.24 |
| 13回推論 | 54.3 | 3.36 |
| 15回推論 | 52.9 | 4.17 |
| 回数制限なし (既存手法) | 50.7 | 1.00 |
表2. 既存手法と推論回数を固定して得られたAgentのtestデータに対する正解率と1問当たりの平均推論時間
| LLM Agent | テストデータの正解率 | 一問あたりの平均推論時間 |
| Chain of Thought | 43.6 | 0.39 |
| Self Consistency with CoT | 49.3 | 1.13 |
| Self Refine | 45.0 | 1.06 |
| LLM Debate | 50.0 | 1.11 |
| Step-back Abstraction | 48.6 | 0.545 |
| Quality Diversity | 43.6 | 0.932 |
| Dynamic Assign of Roles | 47.9 | 0.319 |
表3. baseline手法のtestデータに対する正解率と1問当たりの平均推論時間
まず、図6および表1に示すvalidデータでの評価結果を見ると、推論回数3回の設定で得られたAgentがスコアと平均推論時間のバランスにおいて最も優れていました。次に、図7および表2に示すtestデータにおいてもこの傾向は再現され、推論回数を3回以上に増やした場合、スコアの伸びは緩やかになる一方で、計算コストは増大し続けることが確認できます。これらの結果は、限られた探索イテレーション(本実験では20回)において、性能と処理速度のトレードオフを考慮した場合、Agentの複雑度を推論回数3回程度に設定して最適化することが最も効果的な戦略であることを示唆しています。特に、本手法で得られたAgentは、推論回数を明示的に制御しない既存のMeta Agent Searchの性能を凌駕しており、これはAgentの複雑性を制御してMeta Agent Searchを実施することの有用性を強く裏付けています。
Meta Agent Searchによって発見されたこの最適なAgentアーキテクチャは、図8に示す構造を持っています。このAgentは、多様な解法候補を生成した上で、それらを評価・選択し、最終的な解答を導くという問題解決プロセスを採用しています。
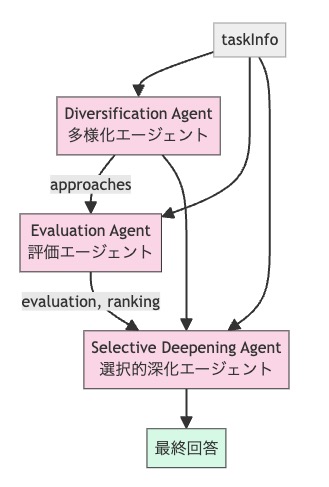
図9. 推論回数3回のAgentの依存関係図
Meta Agent Searchの収束可能性の議論
図6と表1に示す通り、推論回数が4回以上になるとvalidスコアは3回の設定を下回り、探索の収束が困難になることが示唆されます。これは、Agentの複雑化が探索空間を過度に増大させ、有望な解への到達を妨げるためと考えられます。この結果は、別章で述べた進化計算における既知の課題とも一致しており、推論回数を制限して探索空間を限定するアプローチの有効性を裏付けています。
同様の収束性の課題は、推論回数を制限しない既存のMeta Agent Searchでも確認されました。既存手法の探索空間は回数を制限する場合と比べて広大で、20iterationの探索で得られたAgentの推論回数は3~12回と大きくばらつきがありました。その結果、ほぼ同等の推論時間で動作する本手法の「推論回数3回」Agentに比べ、validとtestの両スコアで下回っており、これは探索が十分に収束していないことを意味しています。
最後に
本稿ではADASの概念を導入した論文についての解説を行い、Agentの複雑さの観点からその実運用に向けた検討を実施しました。限られたiteration数で高速且つ高性能なAgentを作成し、さらにそれを活用したより強力なAgentを構成する可能性を示しました。本稿で得られた知見は今後の社内における研究開発やソリューション開発にも活用していく予定です。PFNでは様々なドメインにおけるLLM Agentの社会実装やそれに必要な技術の研究開発を進めています。
今回の取り組みに興味を持っていただいた企業の方はぜひお問い合わせフォームよりご連絡ください。
最後に、Preferred Networks では採用を行っております。今回の記事で興味を持っていただけた方はぜひご応募ください。
- Engineer・Researcher / エンジニア・リサーチャー
- Machine Learning・Optimization・Data Science Engineer/機械学習・最適化・データサイエンスエンジニア
Reference
[1] OpenAI, “Deep Research,” OpenAI. Accessed: Jun. 03, 2025. [Online]. Available: https://openai.com/index/introducing-deep-research/
[2] “GitHub Copilot documentation,” GitHub Docs. [Online]. Available:https://docs.github.com/en/copilot. [Accessed: Jan. 2025].
[3] Y. LeCun et al., “Convolutional Networks for Images, Speech, and Time-Series,” in The Handbook of Brain Theory and Neural Networks, M. A. Arbib, Ed. Cambridge, MA: MIT Press, 1995, pp. 255-258.
[4] J. H. Holland, Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control, and Artificial Intelligence. Ann Arbor, MI: University of Michigan Press, 1975.
[5] F. Chollet, “On the Measure of Intelligence,” arXiv preprint arXiv:1911.01547, Nov. 2019.
[6] D. Dua et al., “DROP: A Reading Comprehension Benchmark Requiring Discrete Reasoning Over Paragraphs,” in Proc. NAACL-HLT, 2019, pp. 2368-2378. arXiv:1903.00161.
[7] F. Shi et al., “Language Models are Multilingual Chain-of-Thought Reasoners,” in Proc. ICLR, 2023. arXiv:2210.03057.
[8] D. Hendrycks et al., “Measuring Massive Multitask Language Understanding,” in Proc. ICLR, 2021. arXiv:2009.03300.
[9] D. Rein et al., “GPQA: A Graduate-Level Google-Proof Q&A Benchmark,” arXiv preprint arXiv:2311.12022, Nov. 2023.
[10] J. Wei et al., “Chain-of-thought prompting elicits reasoning in large language models,” in Proc. 36th Conf. Neural Information Processing Systems (NeurIPS), 2022, pp. 24824-24837.
[11] X. Wang et al., “Self-Consistency Improves Chain of Thought Reasoning in Language Models,” in Proc. ICLR, 2023. arXiv:2203.11171.
[12] A. Madaan et al., “Self-Refine: Iterative Refinement with Self-Feedback,” arXiv preprint arXiv:2303.17651, Mar. 2023.
[13] H. Zheng et al., “Take a Step Back: Evoking Reasoning via Abstraction in Large Language Models,” arXiv preprint arXiv:2310.06117, Oct. 2023.
[14] Y. Du et al., “Improving Factuality and Reasoning in Language Models through Multiagent Debate,” arXiv preprint arXiv:2305.14325, May 2023.
[15] K. I. Chatzilygeroudis et al., “Quality-Diversity Optimization: a novel branch of stochastic optimization,” arXiv preprint arXiv:2012.04322, Dec. 2020.
[16] “Autonomous Agents research papers,” GitHub. [Online]. Available: https://github.com/tmgthb/Autonomous-Agents. [Accessed: Jan. 2025].
[17] OpenAI, “GPT-4 Technical Report,” arXiv preprint arXiv:2303.08774, Mar. 2023.
[18] A. A. Alhejji et al., “Evaluating prompt engineering on GPT-3.5’s performance in USMLE-style medical calculations and clinical scenarios generated by GPT-4,” Scientific Reports, vol. 14, no. 1, p. 17265, Jul. 2024.
[19] Z. Lyu et al., “Efficient Prompting Methods for Large Language Models: A Survey,” arXiv preprint arXiv:2404.01077, Apr. 2024.
[20] K. Cobbe et al., “Training Verifiers to Solve Math Word Problems,” arXiv preprint arXiv:2110.14168, Oct. 2021.
[21] “GSM-Hard: A Mathematical Reasoning Benchmark,” Papers with Code. [Online]. Available:https://paperswithcode.com/dataset/gsm-hard. [Accessed: Jan. 2025].
[22] Anthropic, “Introducing Claude 3 Haiku,” Anthropic Blog, Mar. 2024. [Online]. Available: https://www.anthropic.com/news/claude-3-haiku
[23] OpenAI, “GPT-4 Technical Report,” arXiv preprint arXiv:2303.08774, Mar. 2023.
[24] Anthropic, “Introducing Claude 3.5 Sonnet,” Anthropic Blog, Jun. 2024. [Online]. Available: https://www.anthropic.com/news/claude-3-5-sonnet
[25] W. Long, J. Jiao, X. Liang, and M. Tang, “A space search optimization algorithm with accelerated convergence strategies,” Applied Soft Computing, vol. 25, pp. 103-119, Dec. 2014.
[26] Gao et al., “Omni-MATH: A Universal Olympiad Level Mathematic Benchmark for Large Language Models,” in Proc. Int. Conf. Learn. Represent.* (ICLR), 2025, arXiv:2410.07985.
[27] C. Cartis, E. Massart, and A. Otemissov, “Global optimization using random embeddings,” Mathematical Programming, vol. 199, no. 1-2, pp. 445-488, May 2023.
[28] M. Raghu, B. Poole, J. Kleinberg, S. Ganguli, and J. Sohl-Dickstein, “On the expressive power of deep neural networks,” in Proc. 34th Int. Conf. Machine Learning, vol. 70, 2017, pp. 2847-2854, arXiv:1606.05336.
[29] K. Harada, Y. Yamazaki, M. Taniguchi, T. Kojima, Y. Iwasawa, and Y. Matsuo, “Curse of Instructions: Large Language Models Cannot Follow Multiple Instructions at Once,” submitted to the Int. Conf. on Learning Representations (ICLR), 2025. [Online]. Available: https://openreview.net/forum?id=R6q67CDBCH
Appendix
以下は推論回数1回のADASで得られたAgentのpromptです。
You will solve this mathematical problem by identifying and exploiting mathematical symmetries and invariants. Follow this process exactly:
# PHASE 1: PROBLEM UNDERSTANDING
– Carefully read and understand the problem statement – Identify the mathematical domain (number theory, geometry, algebra, combinatorics, etc.)
– Determine what needs to be calculated or proven
– Identify all given information, constraints, and conditions
– Restate the problem in precise mathematical terms
# PHASE 2: SYMMETRY AND INVARIANT IDENTIFICATION Analyze the problem for the following types of symmetries and invariants:
## NUMERICAL SYMMETRIES – Identify any patterns related to parity (odd/even properties) – Look for divisibility properties or modular patterns
– Check for number-theoretic invariants (remainders, GCD, LCM)
– Examine numerical sequences for recursive patterns or formulas – Consider if the problem exhibits periodicity or cyclic behavior
## ALGEBRAIC INVARIANTS
– Identify quantities that remain unchanged under algebraic operations
– Look for invariant polynomials or expressions
– Check if the problem involves quantities preserved under transformations
– Consider algebraic structures (groups, rings, fields) that might apply
– Examine if the problem exhibits linearity, homogeneity, or other algebraic properties
## GEOMETRIC SYMMETRIES
– Identify any reflectional or rotational symmetries
– Look for translational invariance or scaling properties
– Check for geometric transformations that preserve problem properties
– Consider if the problem can be simplified through coordinate changes
– Examine if the problem exhibits projective or affine invariants
## COMBINATORIAL SYMMETRIES
– Identify ways to count the same set in different ways
– Look for bijections between different representations
– Check for combinatorial identities or principles that apply
– Consider symmetries in counting arrangements or selections
– Examine if the problem exhibits symmetry in inclusion-exclusion principles
## FUNCTIONAL INVARIANTS
– Identify properties preserved under functions or operations
– Look for invariant transformations or mappings
– Check for recurrence relations or functional equations
– Consider fixed points of functions or operations
– Examine if the problem exhibits functional symmetries
# PHASE 3: SYMMETRY EXPLOITATION For each significant symmetry or invariant you’ve identified:
## SYMMETRY/INVARIANT 1: [Name or Description]
– Explain precisely what this symmetry or invariant is
– Describe how it can be exploited to approach the problem
– Develop this approach step-by-step, showing all work
– Note any insights or simplifications that emerge
– Determine if this approach leads to a solution
– If it does, calculate a preliminary answer
## SYMMETRY/INVARIANT 2: [Name or Description]
– Explain precisely what this symmetry or invariant is
– Describe how it can be exploited to approach the problem
– Develop this approach step-by-step, showing all work
– Note any insights or simplifications that emerge
– Determine if this approach leads to a solution
– If it does, calculate a preliminary answer
## SYMMETRY/INVARIANT 3: [Name or Description]
– Explain precisely what this symmetry or invariant is
– Describe how it can be exploited to approach the problem
– Develop this approach step-by-step, showing all work
– Note any insights or simplifications that emerge
– Determine if this approach leads to a solution
– If it does, calculate a preliminary answer
# PHASE 4: APPROACH SELECTION AND REFINEMENT
– Evaluate which symmetry-based approach is most promising
– Consider which approach provides the most insight or elegance
– Select the approach that leads most directly to a solution
– If multiple approaches yield different answers, reconcile the differences
– Refine the selected approach to ensure mathematical rigor
# PHASE 5: COMPLETE SOLUTION
– Fully develop the most promising symmetry-based approach
– Show all mathematical work clearly and precisely
– Verify that your solution correctly exploits the identified symmetry or invariant
– Check that your solution addresses all aspects of the original problem
– Ensure all calculations are accurate and all reasoning is sound
– Arrive at a final answer that is mathematically justified
# FINAL ANSWER
State your final numerical answer clearly. Make sure it’s an integer or decimal that can be parsed with float().
Tag