Blog
本記事は 2020 年夏季インターンシップに参加された 鈴木 海渡 さんによる寄稿です。
こんにちは。PFN の 2020 年夏季インターンシップに参加した、東北大学 M1 の鈴木 海渡です。大学では、強化学習や計算論的学習理論の研究をしています。
今回のインターンシップでは、「メタ強化学習を用いたダイナミクスの変化への適応」というテーマで研究を行いました。この記事では、その内容と実験結果について簡単に紹介させて頂きたいと思います。
1. 背景
学習者であるエージェントが逐次的に行う行動によって状態が変化していく問題設定を考えます。このような問題設定における最適化手法の 1 つとして、強化学習があります。近年深層学習との組み合わせによって強化学習の適用範囲は大きく広がり、盛んに研究が行われています。代表的な応用先として、囲碁をはじめとしたボードゲーム [1, 2, 3, 4] 、ビデオゲーム [4, 5, 6] 、ロボットの制御 [7, 8] 、タクシーの配車の最適化 [9] などがあります。
しかしながら、強化学習を実世界の問題に応用する上では、まだ多くの課題が残されています。その 1 つとして、環境の変化に脆弱であるという課題が挙げられます。例えば、シミュレーション上で学習したモデルを現実世界にそのまま適用しても、シミュレータが表現しきれない外観やダイナミクスの差によって性能は大きく劣化します。
この課題に対するアプローチの 1 つとして、多様な環境で学習し、各環境に効率良く適応する方法を学習するメタ強化学習という枠組みが存在します。今回のインターンシップでは、メタ強化学習を用いて環境のダイナミクスの変化への適応に取り組みました。
2. メタ強化学習
強化学習では、エージェントが環境中で行動し、それに応じて次の状態と報酬が返ってくる、という問題設定において、報酬の総和を最大化することを目指して学習を行います。学習対象となるのは、方策という状態 \(s\) で条件付けた行動 \(a\) の確率分布 \(\pi(a | s, z)\) です。ここで、 \(z\) は方策のパラメータです。
メタ強化学習では環境(以下タスク)の分布を考え、分布内の各タスクに対して効率良く適応する方法を学習します。通常の強化学習では、あるタスク \(k\) を解けるように学習した方策のパラメータ \(z_k\) は、必ずしも他のタスク \(k’(\neq k)\) にそのまま利用できるわけではなく、多くの場合タスクが変われば学習しなおす必要があります。しかしながら、タスクごとに \(z_k\) を学習し直していると効率が悪いため、メタ強化学習では、タスクに非依存のパラメータ \(\theta = (\theta_{enc}, \theta_{\pi})\) を導入し、\(\theta_{enc}\) を用いて効率よく \(z_k\) の推論を行います。方策は \(\theta_{\pi}\) と \(z_k\) を用いて \(\pi(a | s, \theta_{\pi}, z_k)\) としてモデル化します。
例えば、有名なメタ学習手法である MAML [10] は、\(\pi(a | s, \theta_{\pi}, z_k) = \pi(a | s, z_k)\) とし、方策はタスク依存のパラメータ \(z_k\) にのみ依存すると考える一方、以下のように勾配法を用いてタスク非依存のパラメータ \(\theta_{enc}\) を用いて \(z_k\) を推論するものと捉えることができます [11] 。ここで、 \(D_k\) はタスク \(k\) で得られた経験データで、 \(\varepsilon\) はステップサイズ、 \(Loss(z_k; D_k)\) は 方策パラメータ\(z_k\) に関するタスク\(k\)の損失関数です。
\[z_k \leftarrow \, \theta_{enc} \, – \, \varepsilon \, \left. \frac{\partial Loss(z_k; D_k)}{\partial z_k}\right|_{z_k=\theta_{enc}}\]
行動の決定は、更新後のタスク依存のパラメータ \(z_k\) を用いて行います。
\[a \sim \pi(a | s, z_k) \]
別のアプローチとして、タスク \(k\) の経験 \(D_k\) から \(z_k\) を推論するエンコーダ \(p(z_k | \theta_{enc}, D_k)\) を陽にニューラルネットワーク等でモデル化して学習することも考えられます [12, 13] 。ここで、 \(\theta_{enc}\) はタスク非依存のパラメータのうち、エンコーダのパラメータです。この場合、 \(z_k\) は単にエンコーダが表現する確率分布からのサンプルとして得られます。
\[z_k \sim p(z_k | \theta_{enc}, D_k)\]
行動の決定は、エンコーダが表現する確率分布から得られた \(z_k\) を方策に入力して行います。ここで、 \(\theta_{\pi}\) はタスク非依存のパラメータのうち、方策のパラメータです。
\[a \sim \pi(a | s, \theta_{\pi}, z_k), z_k \sim p(z_k | \theta_{enc}, D_k)\]
このアプローチの場合、MAML と異なり \(z_k\) の計算に勾配計算を必要とせず、エンコーダが表現する確率分布からのサンプルが容易に得られるならば、 \(z_k\) を容易に取得することができます。今回のインターンシップではこのアプローチを用いたメタ強化学習アルゴリズムについて調べています。
エンコーダを陽に用いたメタ強化学習では、エンコーダの学習をどのように行うかや、エンコーダとしてどのようなモデルを用いるかなど、様々なアルゴリズム構成上の自由度があります。しかしながら、多くの手法は異なる強化学習アルゴリズムをベースにして学習され、さらに異なるタスク分布で検証されているため、どのような条件でどのような構成が有効なのかは定かではありません。
そこで今回のインターンシップでは、条件を揃えた上でメタ強化学習における様々な構成の有効性を実験的に検証しました。以下では、その中でも特にエンコーダの設計に着目し、損失関数とエンコーダの確率性に関する取り組みを紹介します。
3. エンコーダの設計
3.1. 損失関数
エンコーダはニューラルネットワークでモデル化し、確率的勾配法によって学習します。しかしながら、タスク固有のパラメータ \(z_k\) に対する教師信号は必ずしも与えられないため、エンコーダは直接的な教師あり予測誤差以外の何らかの損失関数によって学習を行う必要があります。
PEARL [12] では、行動価値関数(Q関数)の入力に \(z_k\) を結合し、以下のように、TD 誤差が小さくなるようにエンコーダの損失関数を設計します。TD 誤差 \(r_{t+1} + \gamma Q(s_{t+1}, a_{t+1}, z_k) \, – Q(s_t, a_t, z_k)\) は、行動価値(状態 \(s_t\) と行動 \(a_t\) で条件付けた報酬 \(r_{t+1}\) の総和の期待値)が正しく予測できていればその期待値が 0 になる誤差で、強化学習において頻出する概念の 1 つです。ここで、 \(\gamma\) は報酬の総和をとる際に将来の時刻の報酬を割り引くためのパラメータ(割引率)で、下付き文字の \(t\) は時刻を表します。
\[\mathbb{E}_{p(z_k | \theta_{enc}, D_k)} [(r_{t+1} + \gamma Q(s_{t+1}, a_{t+1}, z_k) \, – Q(s_t, a_t, z_k))^2]\]
MANGA [13] では、現在の状態と行動、\(z_k\) から次の状態を予測する状態遷移モデル \(s_{t+1} = \mathcal{F}(s_t, a_t, z_k)\) が所与であると仮定し、 以下のように状態予測誤差が小さくなるようにエンコーダの損失関数を設計します。
\[\mathbb{E}_{p(z_k | \theta_{enc}, D_k)} [(s_{t+1} \, – \mathcal{F}(s_t, a_t, z_k))^2]\]
これらの損失関数から Reparametrization Trick [14] を用いてエンコーダのパラメータ \(\theta_{enc}\) に勾配を伝播して学習を行います。どちらの手法も、上記の損失関数に加えて \(p(z_k | \theta_{enc}, D_k)\) と事前分布( \(\mathcal{N} (\boldsymbol{0}, I)\) など)との間の KL ダイバージェンスによる正則化が入っています。
今回のインターンシップでは、強化学習アルゴリズム及び検証に用いるタスク分布を揃え、TD 誤差と状態予測誤差のそれぞれの損失関数について、性能への影響を検証しました。ただし、より一般的な設定に適用可能にするため、MANGA と異なり状態遷移モデルは所与とせず、状態遷移モデルもニューラルネットワークでモデル化して学習しています。また、2 つの損失関数の組み合わせによる性能の改善にも挑戦しました。
3.2. エンコーダの確率性
メタ強化学習の分野において、エンコーダ \(p(z_k | \theta_{enc}, D_k)\) は基本的に確率的なモデルとして設計されています。この場合、学習されたエンコーダを利用した行動の決定方法として、例えば以下の 3 つが考えられます。
- サンプリング(Sample): \(\pi(a | s, \theta_{\pi}, z_k), z_k \sim p(z_k | \theta_{enc}, D_k)\)
- 平均の入力(Mean): \(\pi(a | s, \theta_{\pi}, \mathbb{E}_{p(z_k | \theta_{enc}, D_k)}[z_k])\)
- 予測分布の期待値の利用(Predictive): \(\mathbb{E}_{p(z_k | \theta_{enc}, D_k)}[\pi(a | s, \theta_{\pi}, z_k)]\)
これらの手法同士の性能を比較するため、今回実装したメタ強化学習手法の 1 つについて、同じ学習済み重みに対し、行動の決定方法だけを変更してテストを行った予備実験の結果を以下に示します(予備実験の設定は後述の実験設定と同じものとしています)。予測分布の期待値については、 \(p(z_k | \theta_{enc}, D_k)\) から 100 回のサンプリングを行うことによるモンテカルロ積分で近似しています。
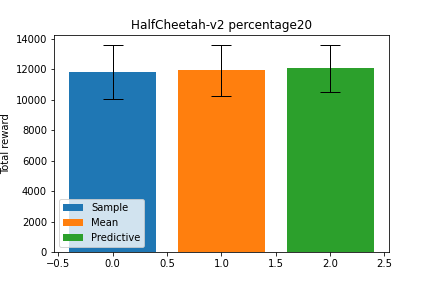
結果は上図のように、いずれもほとんど性能が変わらないという結果になりました。この予備実験の結果から、エンコーダが表現する確率分布 \(p(z_k | \theta_{enc}, D_k)\) の平均以外の部分はほとんど有用な情報を含んでいないことが示唆されます。
この予備実験の結果を元に、エンコーダとして決定的なモデル \(z_k = f(\theta_{enc}, D_k)\) を用いても確率的な場合と同等以上の結果が得られるのではないかと考え、実装して検証しました。
4. 実験
4.1. 実験設定
検証には MuJoCo [15] の HalfCheetah-v2 を用い、ダイナミクスパラメータ(重力加速度、質量、慣性モーメント、摩擦係数、剛性係数、減衰係数)を ±10%、20%、30% の範囲で一様ランダムに変動させてそれぞれのタスク分布としました。訓練時にはダイナミクスパラメータをエピソードごとに変更しながら学習を行いました。強化学習アルゴリズムとして SAC [16] を用いました。学習は 5e6 ステップ行い、各タスク分布、比較手法ごとに訓練時のシード値を変えて 25 回実施しました。実装は PFN が公開している強化学習フレームワークである PFRL 上で行っています。
4.2 ベースラインとの比較
まず実装がうまく動作していることを確認するため、今回実装したメタ強化学習手法の 1 例(TD-Det)をベースラインと比較します。ここで、TD はエンコーダの学習に TD 誤差の最小化を行う損失関数を用いたこと、Det は決定的なエンコーダを用いたことを意味します。
ベースラインとしては、タスク分布内のどのタスクに対してもうまく動作するロバストな方策を一つ獲得する Domain Randomization [17](DR)及び、変動させたダイナミクスパラメータが常に既知であるという強い仮定を置き、それを観測に直接結合して強化学習を行った手法(Privileged)を用います。
学習済み重みを 100 通りの異なるテストタスクで評価した結果を以下に示します。各テストタスクにおいて 10 エピソードの報酬の総和の平均を評価し、その値を全テストタスクで平均したものを 1 つの訓練シードのスコアとし、その平均を表示しています。エラーバーは訓練シード間での標準偏差の大きさを表しています。
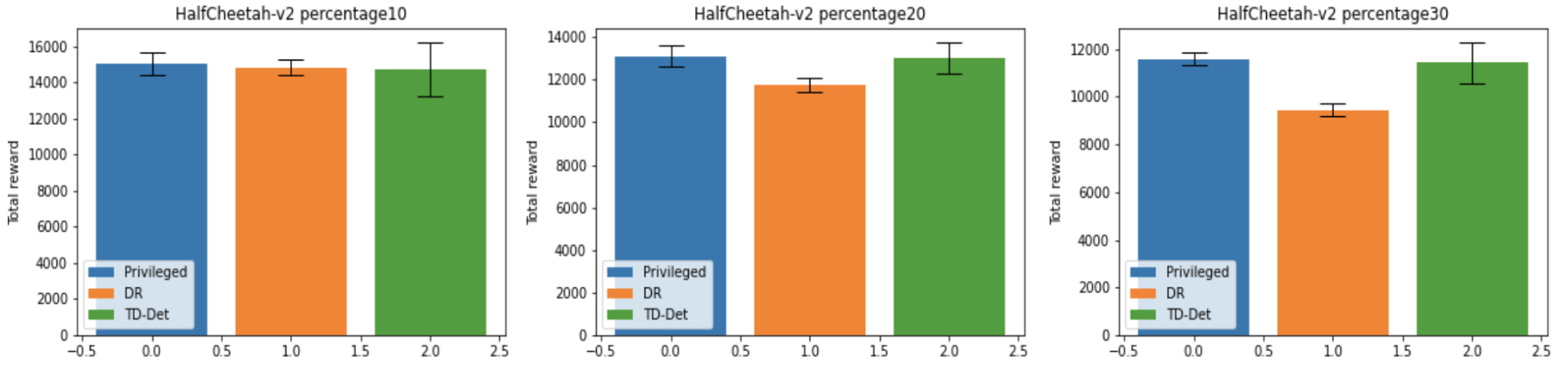
上図に示されているように、ダイナミクスパラメータの変動幅が大きくなると、単一の方策を用いる DR よりも、タスクに応じて方策の挙動を適応させることができる TD-Det の方がうまく動作し、Privileged に匹敵する性能を示すことが確認できました。
4.3. 損失関数
エンコーダの学習における損失関数として、先述した TD 誤差(TD-Stoc)及び状態予測誤差(SP-Stoc)に加え、その2つの組み合わせ(BothShare-Stoc, BothSep-Stoc)を実装し、性能を検証しました。ここで、SP はエンコーダの学習に状態予測誤差の最小化を行う損失関数を用いたこと、Both は TD 誤差の最小化を行う損失関数と状態予測誤差の最小化を行う損失関数の両方を同時に用いたこと、Stoc はエンコーダに確率的なものを用いたことを表します。
また、2 つの損失関数を組み合わせたときには、損失関数間でエンコーダのネットワークを共有したもの(BothShare-Stoc)のほかに、損失関数の干渉による性能劣化を懸念し、損失関数の種類ごとに異なるエンコーダのネットワークを用いて、方策には両方のエンコーダから得られたエンコード結果を結合して入力する手法(BothSep-Stoc)を実装し、その性能を検証しました。BothSep-Stoc では、 \(z_k\) の次元の半分を TD 誤差に、残りの半分を状態予測誤差に割り当てています。
学習済み重みを 100 通りの異なるテストタスクで評価した結果を以下に示します。
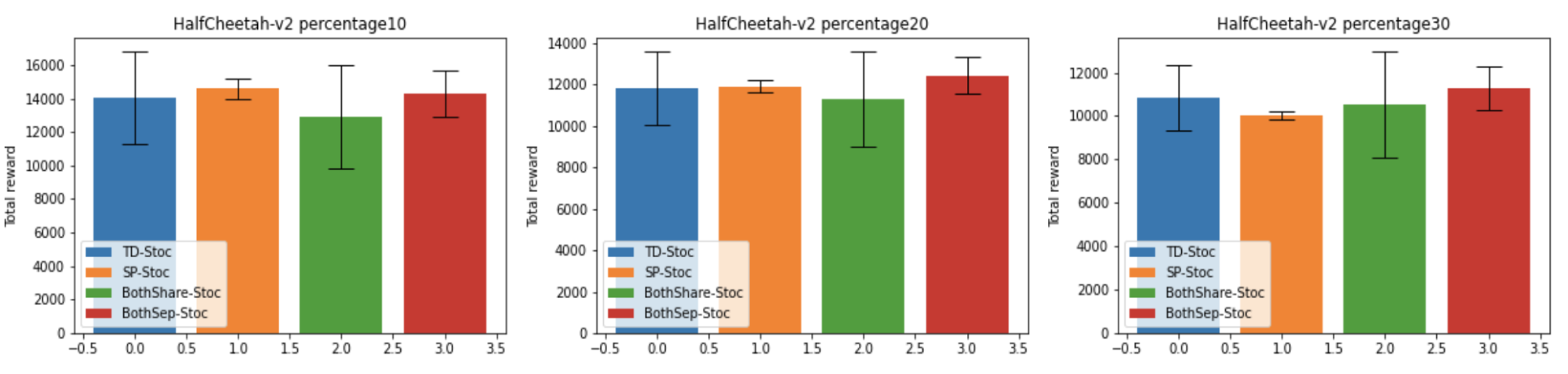
まず TD-Stoc と SP-Stoc を比較すると、ダイナミクスの変動幅によってどちらの損失関数が優越するかが変動しつつも、変動幅 30% では TD-Stoc がはっきりと良い性能を示しています。これは、今回は状態遷移モデルも学習しているため、変動幅が大きくなり状態遷移の予測が難しくなったためであると考えられます。しかしながら、SP-Stoc の方が、訓練シード間での結果の分散は明らかに小さく抑えられています。これは、教師信号として誤差を含む自身の出力を参照する(ブートストラップ)を行う TD-Stoc より、常に正確な教師信号が与えられる SP-Stoc の方が安定した学習ができるためであると考えられます。
2 つの損失関数の組み合わせについては、単純な組み合わせである BothShare-Stoc では、損失関数同士が干渉しあってしまったためか、それぞれの損失関数を単体で用いるよりも性能が下がる場合の方が多く、また訓練シード間での分散が非常に大きくなってしまっています。これに対し、ネットワークを分けた BothSep-Stoc では、全体としてそれぞれの損失関数を単体で用いた場合とほぼ同等かより優れた結果を示し、訓練シード間での分散も比較的小さく抑えられています。
4.4. エンコーダの確率性
確率的なエンコーダ(TD-Stoc)と決定的なエンコーダ(TD-Det)それぞれの学習曲線を以下に示します。損失関数は、両方とも TD 誤差に固定しています。学習曲線においては、各訓練シードごとに学習全体を通して常に同じテストタスクを用いています。
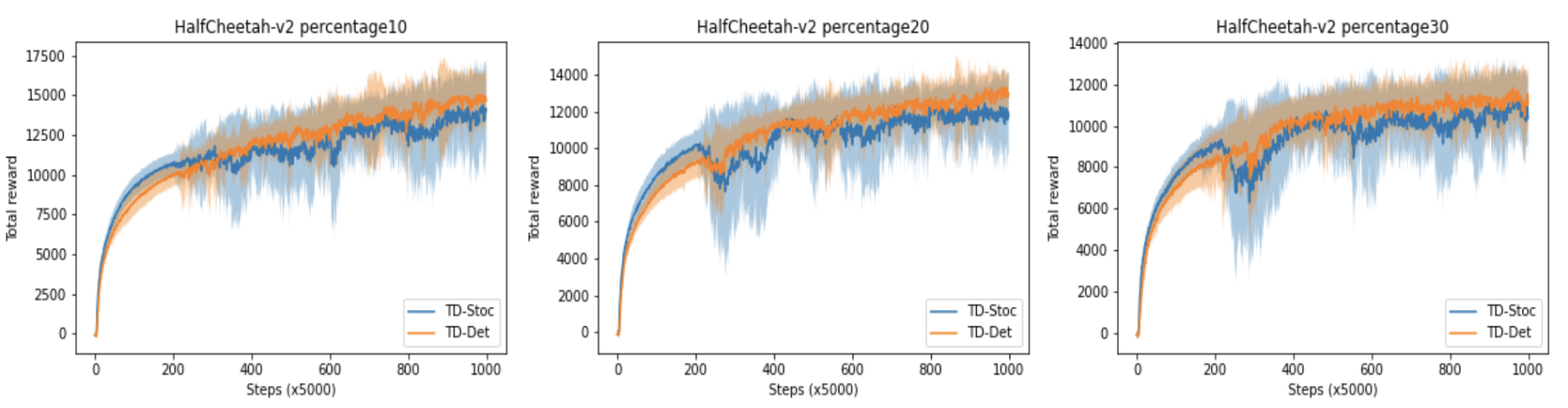
探索上に多少の不利があるのか、初期の学習速度では TD-Stoc に分がありますが、最終性能では TD-Det が勝ることがわかりました。
学習済み重みを 100 通りのテストタスクで評価した結果を以下に示します。
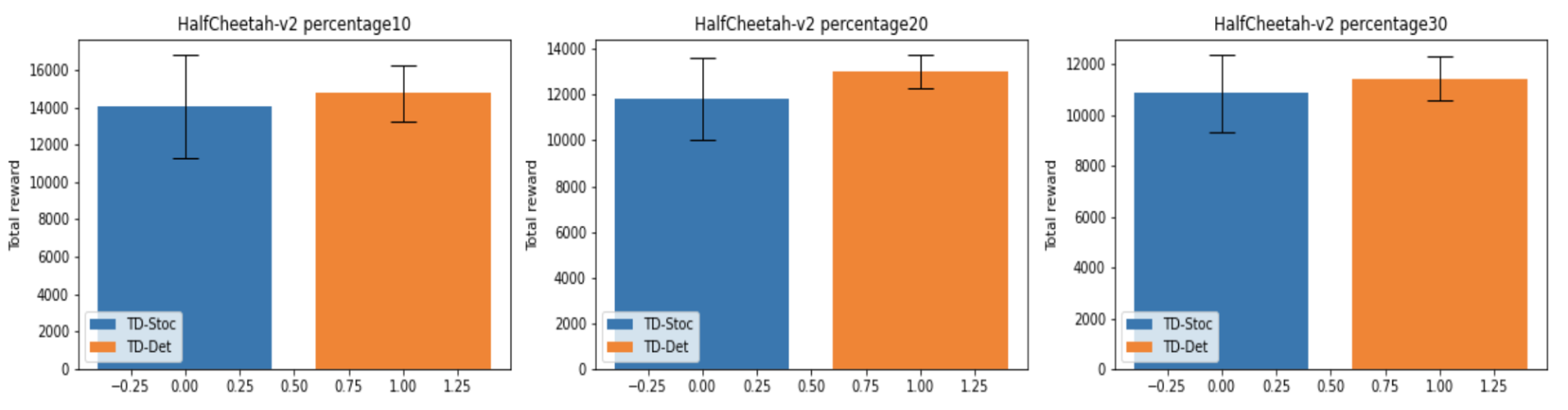
ダイナミクスパラメータの変動幅に関わらず、性能及び学習シードごとの結果の分散においても一貫して TD-Det が優位であることが確認できました。
5. まとめと今後の方向性
今回のインターンシップでは、ダイナミクスの変化に適応するため、メタ強化学習の分野に取り組み、エンコーダを陽に用いたメタ強化学習における損失関数、エンコーダの確率性などの構成の性能への影響を実験的に検証しました。損失関数に関する実験の結果として、今回はタスクの変動がダイナミクスであるにも関わらず、実験条件によっては TD 誤差が有効であること、状態予測誤差を用いることで訓練シード間での結果の分散を抑えることができること、ネットワークを分けることで 2 つの損失関数を効果的に組み合わせられることが確認できました。エンコーダの確率性に関する実験の結果として、決定的なエンコーダが、一貫して確率的なエンコーダよりも優れた性能を示すことが確認できました。
今後の方向性として、より多様なタスクで実験し、結果の検証を行うことが挙げられます。HalfCheetah-v2 以外の MuJoCo タスクでの実験や、ダイナミクスではなく報酬を変更したタスクでの実験も小規模には行っていましたが、今回 HalfCheetah-v2 で行なったような大規模な実験を行い結果をまとめるところまでは行き着きませんでした。
また、決定的なエンコーダを用いた場合、PEARL [12] で言及されているように探索上のデメリットが発生する場合があると考えられるため、MAME [18] で行なっているように探索用の方策を別に用意するなども、興味深い今後の方向性の 1 つです。
感想と謝辞
メタ強化学習は、興味は持っていながらもこれまで深堀りしたことがなかった分野なので、今回のインターンシップでサーベイ、実装等を行う過程で多くの新しい知見を身に付けることができました。ここまで大規模な実験を行ったことがなかったため、バグや実験実施上の不手際もかなりありましたが、それも含めて良い経験だったと思っています。
メンターの前田さんと城下さんには、研究方針に関する議論から実装上の細かい話まで手厚くサポートして頂きました。エンジニアの藤田さんには、PFRL の話を始め実装面で数多くのアドバイスを頂きました。また、実験的な研究だったこともあり、PFN の計算機クラスター、及びクラスターチームの皆さんにも大変お世話になりました。この場を借りてお礼申し上げます。
参考文献
[1] D. Silver, et al., “Mastering the game of Go with deep neural networks and tree search,” Nature, 529(7587):484–489, 2016.
[2] D. Silver, et al., “A general reinforcement learning algorithm that masters chess, shogi, and go through self-play,” Science, 362(6419):1140–1144, 2018.
[3] D. Silver, et al., “Mastering the game of go without human knowledge,” Nature, 550:354–359, 2017.
[4] J. Schrittwieser, et al., “Mastering Atari, Go, Chess and Shogi by Planning with a Learned Model,” arXiv preprint arXiv:1911.08265, 2019.
[5] V. Minh, et al., “Human-level control through deep reinforcement learning,” Nature, 518(7540): 529–533, 2015.
[6] V. Minh, et al., “Asynchronous Methods for Deep Reinforcement Learning,” in ICLR, 2016.
[7] D. Kalashnikov, et al., “QT-Opt: Scalable Deep Reinforcement Learning for Vision-Based Robotic Manipulation,” in CoRL, 2018.
[8] Y. Fujita, et al., “Distributed Reinforcement Learning of Targeted Grasping with Active Vision for Mobile Manipulators,” in IROS, 2020.
[9] Z. Xu, et al., “Large-Scale Order Dispatch in On-Demand Ride-Hailing Platforms: A Learning and Planning Approach,” in KDD, 2018.
[10] C. Finn, et al., “Model-Agnostic Meta-Learning for Fast Adaptation of Deep Networks,” in ICML, 2017.
[11] S. Maeda, et al., “Meta Learning as Bayes Risk Minimization,” arXiv preprint arXiv:2006.01488, 2020.
[12] K. Rakelly, et al., “Efficient Off-Policy Meta-Reinforcement Learning via Probabilistic Context Variables,” in ICML, 2019.
[13] H. Bharadhwaj, et al., “MANGA: Method Agnostic Neural-policy Generalization and Adaptation,” in ICRA, 2020.
[14] D. P. Kingma, et al., “Auto-Encoding Variational Bayes,”, in ICLR, 2014.
[15] E. Todorov, et al., “Mujoco: A physics engine for model-based control,” in IROS, 2012.
[16] T. Haarnoja, et al., “Soft Actor-Critic Algorithms and Applications,” arXiv preprint arXiv:1812.05905, 2018.
[17] J. Tobin, et al., “Domain randomization for transferring deep neural networks from simulation to the real world,” in IROS, 2017.
[18] S. Gurumurthy, et al., “MAME : Model-Agnostic Meta-Exploration,” in CoRL, 2019




