Blog
This post is contributed by Shota Imaki, who was an intern and a part-time engineer at PFN. Japanese version is available here.
I am Shota Imaki, a Ph.D. student majoring in theoretical physics. During my internship, we studied Deep Hedging, which had captured my interest for a long time, and I am writing this to summarize this work.
Deep Hedging is a grand-breaking framework to hedge financial derivatives using deep learning. It has, however, been notorious for the difficulty of training. We proposed a “no-transaction band network” to achieve a 20x speedup of training. Deep Hedging can now learn to hedge and price exotic derivatives in seconds.
To our great honor, we receive the Incentive Award of the Japanese Society of Artificial Intelligence (JSAI) for this research. We released minimal implementation of the work as well as a PyTorch-based library for Deep Hedging, PFHedge.
- Paper for JSAI (in Japanese): Neural Network Architecture for Efficient Deep Hedging
- Paper: No-Transaction Band Network: A Neural Network Architecture for Efficient Deep Hedging
- Minimal Implementation: pfnet-research/NoTransactionBandNetwork
- Deep Hedging Library: pfnet-research/pfhedge
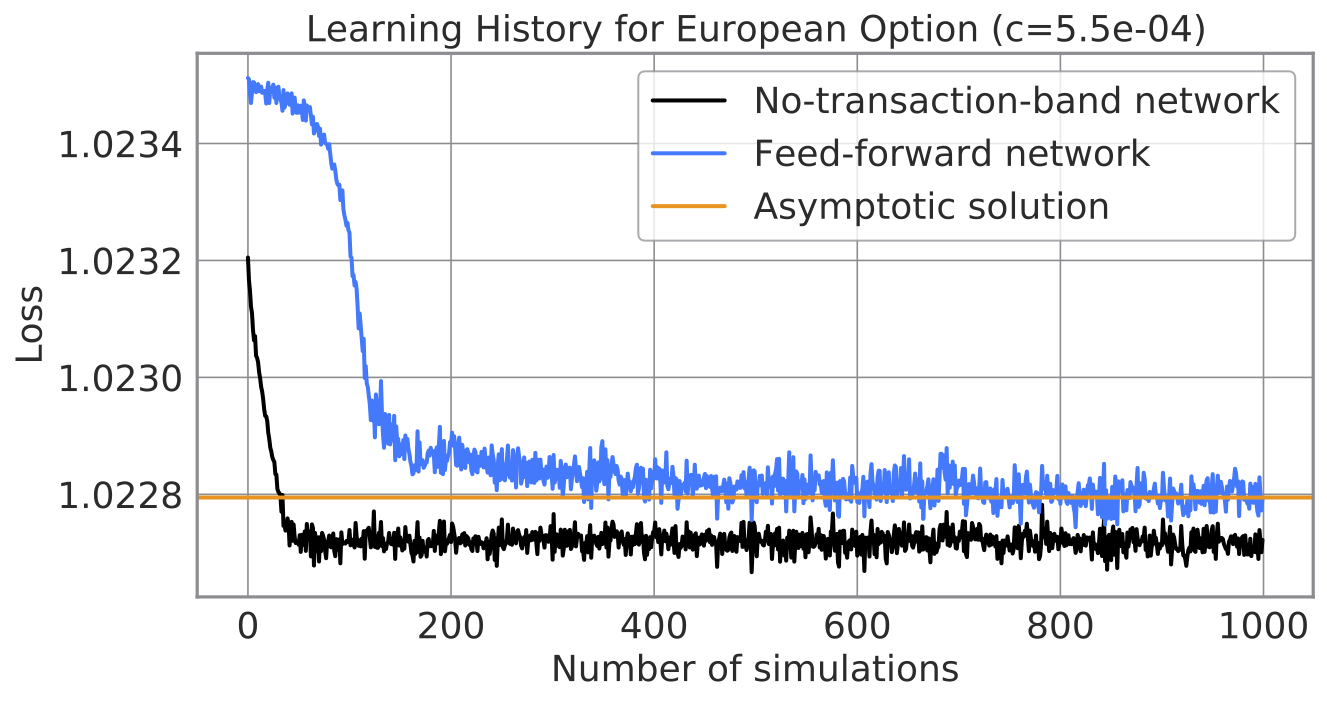
Learning histories of a neural network in a preceding paper (blue) and our neural network (black).
Research Objective: Hedging Automation
Our research aims to automate hedging associated with securities companies’ dealing in derivatives. Let us first describe what derivatives are, how hedging works, and how Deep Hedging automates it.
Derivative
Derivatives are securities derived from ordinary securities such as equities, bonds, and currencies. An equity derivative, for example, settles a payoff that depends on the trajectory of the equity price. Examples include the following options:
- European call option: It pays off \(\max(S – K, 0)\) where \(S\) is the final price in a predetermined time horizon and \( K\) is a strike price.
- Lookback call option: It pays off \(\max(M – K, 0)\) where \(M\) is the maximum price in a predetermined time horizon and \(K\) is a strike price.
Derivatives enable pliant insurance and investment. Entities may use derivatives to insure against their uncertain cash flow or balance; Investors may flexibly make their position with derivatives. Derivatives are indispensable instruments for modern risk management and advanced investments. That is why derivatives have thrived for a long to develop their trillion-dollar global market.
Hedging
Securities companies sell derivatives, say an equity derivative, to counterparties and usually hedge the resulting short position. The value of the equity derivative fluctuates with some “sensitivity” to the underlying equity. Therefore, a securities company can offset the risk of the derivative by transacting the right amount of equity. That is how hedging works.
In an idealized market without transaction cost or other frictions, one can precisely compute the optimal hedging strategy. It is optimal to perfectly offset the risk with incessant trades that cancel out the “sensitivity” calculated based on financial models.
The real market, in contrast, has transaction costs and thereby makes hedging optimization much harder. Human traders need to manually adjust quantitative models based on their experiences to account for the incompleteness of the market.
Hedging automation is thus a crucial task because manual hedging has essential drawbacks such as high labor costs and limited order volumes.

A hedging strategy represented by a human brain.
Existing Work: Deep Hedging
Deep Hedging (Buehler et al. 2018) is a deep learning-based framework to automate hedging. It represents a hedging strategy with a neural network and seeks the optimum by improving parameters therein. Deep Hedging expects to slash up to 80% of costs and attracts high hopes as a “game-changer” of the derivatives business.
A hedging strategy represented by a neural network.
However, such optimization is easier said than done in practice. In quite a few cases, a neural network struggles to converge even after a considerable amount of training. It is a fatal problem for securities companies that have the mandate to undertake their customers’ orders quickly while accurately.
That is why we proposed a novel neural network that facilitates fast training in Deep Hedging. Proposed network attains 20x speedup in comparison to the preceding neural network.
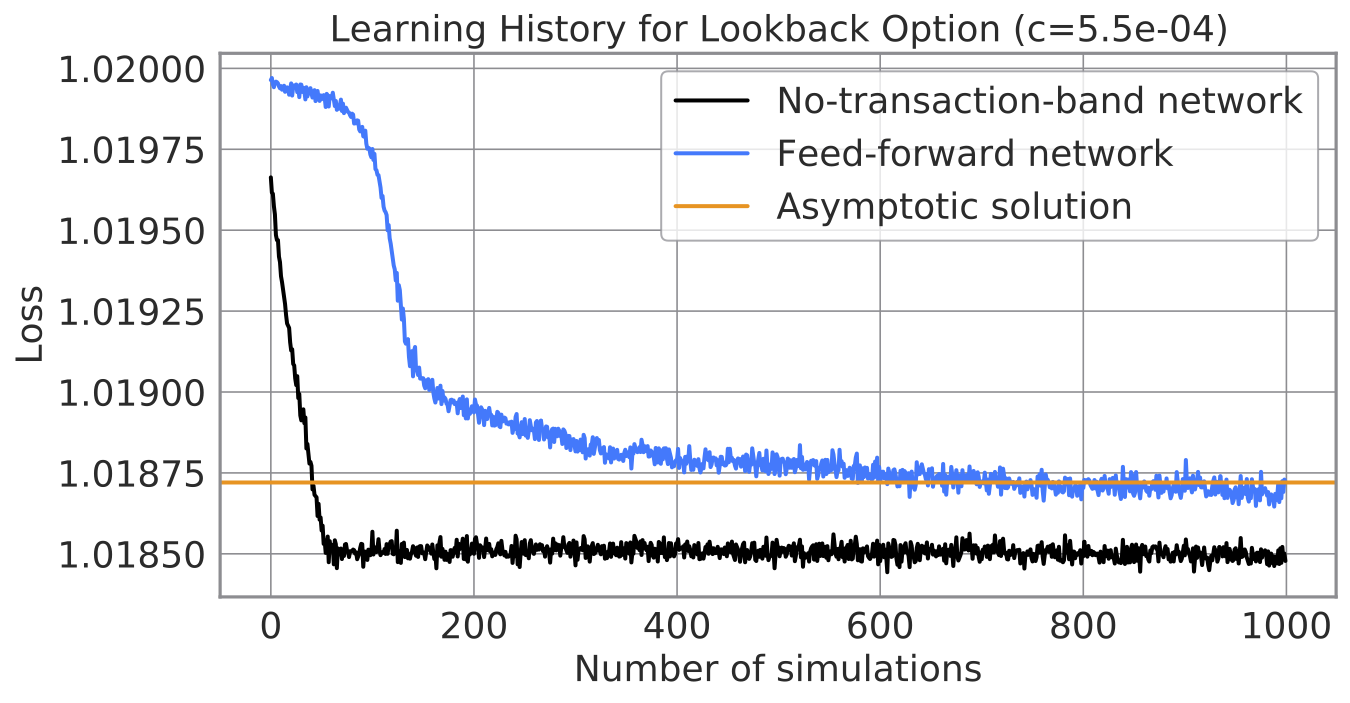
Learning curves of a neural network proposed in the original paper (blue) and our network (black).
Hedging Optimization
Let us now formulate the hedging optimization. Note that the formulation below is abridged from that in the original paper.
A securities company sells a derivative to its customer and hedges the associated risk by transacting the underlying asset. So transactions at time steps \(t = 0,\, \dots\, , T\) give rise to the following final profit. The overall payoff is determined by the profit from the derivative, transaction of the underlying asset, and transaction cost.
\[P = -Z + \sum_{t = 0}^{T – 1} (\delta_t \Delta S_t – c |\Delta \delta_t| S_t)\]
Here, \(Z\) is the terminal value of the derivative (which is a function of the stock price trajectory), \(\delta\) is a unit of stocks hold at each time step, \(S\) is the stock price, and \(c\) is the transaction cost rate. Notice that \(P\) is a random variable as the stock price is assumed so.
The risk measure is the following loss function with \(u\) being a utility of the securities company. The optimal hedging strategy is the one minimizing this loss.
\[\ell(\delta) = -\mathbf{E} [u(P)]\]
In other words, the optimal hedge maximizes the expected utility. Because the utility is monotone and convex, one has to increase the mean of the profit while quenching deviation. Since frequent re-hedging suppresses risk but increases transaction cost, one should re-hedge in the apt interval.
Deep Hedging
The central idea of Deep Hedging is to represent a hedging strategy \(\delta\) by a neural network. The network proposed in the original paper inputs the market information and the current position. The output is the position at the next time step.
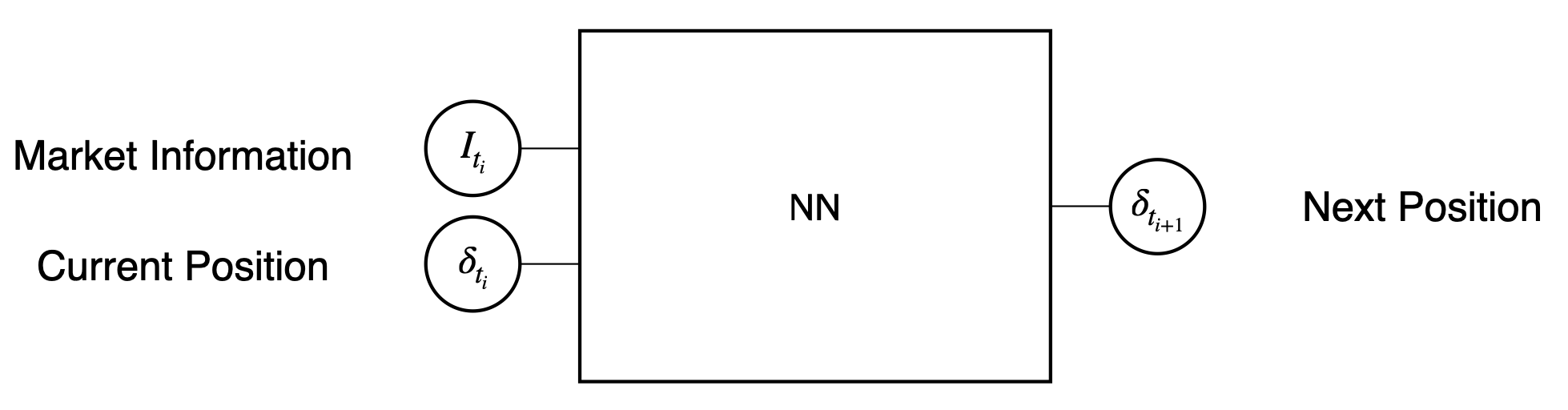
A schematic figure of the neural network proposed in the original paper.
The neural network can approximate the optimal hedge through training. That is, we may want to simulate the path of stock prices, let the neural network hedge against them, and then tweak parameters therein to reduce the loss.
However, this optimization is easier said than done in practice. As shown in the learning history on top, it may not converge even after iterating 1,000 simulations. We conjectured that the difficulty is because the inputs depend on the current position. A neural network struggles until it observes many paths for which a neural network makes various outputs.
Proposal: No-Transaction Band Network
We proposed a “no-transaction band network”, a neural network that overcomes the difficulty of position-dependence. This architecture is as simple as follows.
- A neural network inputs the market information and outputs a permissible band of the next position, \([b_{\text{l}}, b_{\text{u}}]\).
- The next position is obtained by clamping the current position into the band.
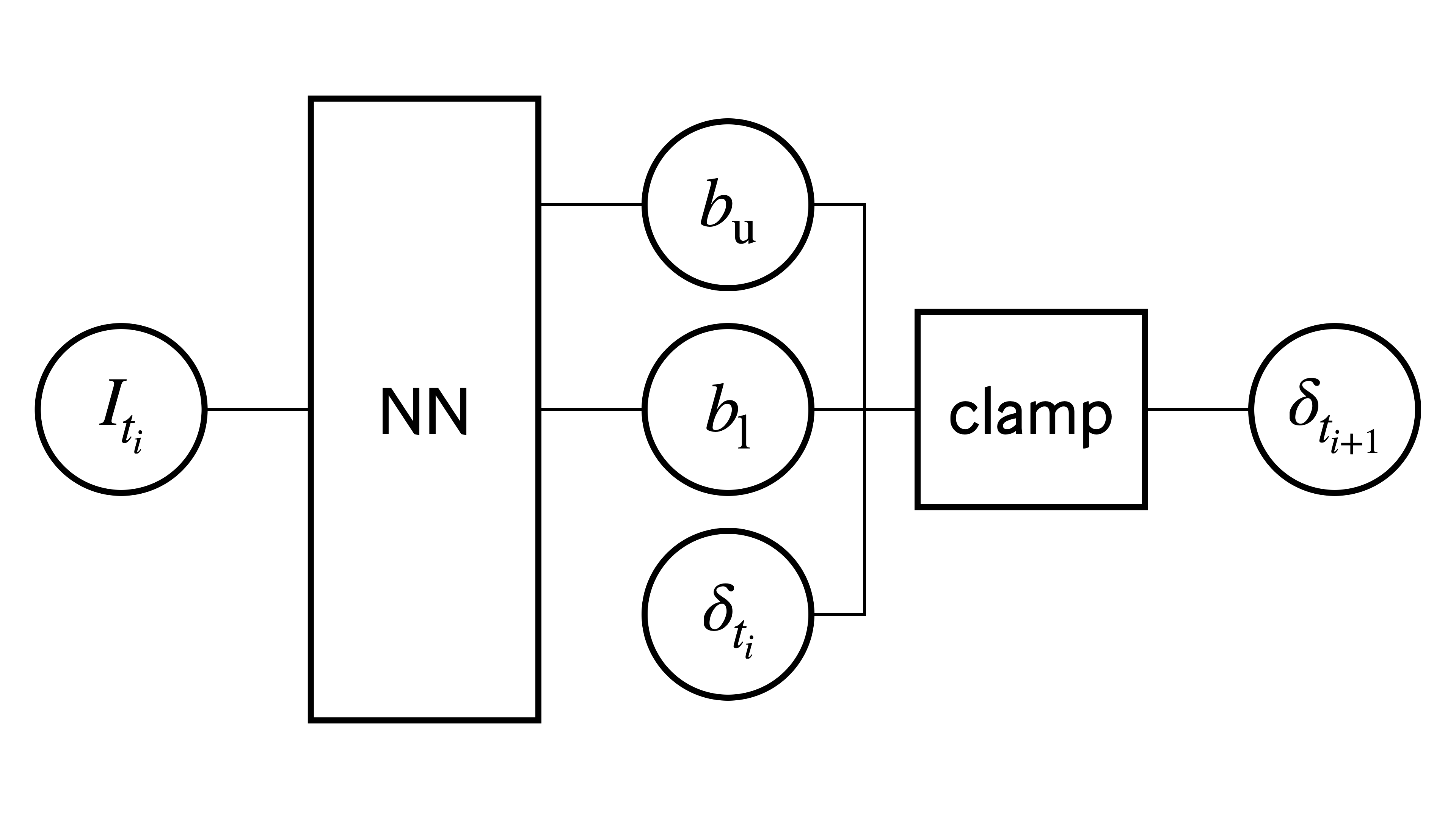
A schematic figure of a no-transaction band network.
Here the \(\mathsf{clamp}\) function reads as follows. PyTorch implements it as \(\mathsf{clamp}\).
\[\mathsf{clamp}(\delta_{t_i}, b_{\text{l}}, b_{\text{u}})
= \begin{cases}
b_{\text{l}} & \text{if } \delta_{t_i} < b_{\text{l}} \\
\delta_{t_i} & \text{if } b_{\text{l}} \leq \delta_{t_i} \leq b_{\text{u}} \\
b_{\text{u}} & \text{if } \delta_{t_i} > b_{\text{u}}
\end{cases}\]
The no-transaction band network has two advantages.
- Neural network’s inputs do not depend on the current position: This feature overcomes the difficulty of position-dependence to facilitate training.
- Neural network encodes an efficient strategy: Strategy using a band is cost-effective because it never transacts inside the band. A Neural network encodes this wisdom as an “induction bias.”
Let us remark on the second advantage before leaving this section. This strategy has long been studied as a “no-transaction band strategy” and proved to be optimal for European options and exponential utility. We theoretically proved that this strategy is optimal for a broader class of derivatives and utilities as well. This proof, along with the universal approximation theorem, guarantees that the no-transaction band network can represent the optimal hedging strategy. It is an indispensable guarantee for securities companies, which are mandated to offer the best price to their customers through the optimal hedge.
Numerical Experiment
We performed numerical simulations to demonstrate the efficiency of the no-transaction band. We compare the following hedging methods for European and lookback options.
- Deep Hedging with the No-Transaction Band Network: The proposed method.
- Deep Hedging with an Ordinary Feed-forward Network: The method proposed in the orignal paper of Deep Hedging.
- Asymptotically Optimal Hedging Strategy: The optimal strategy for an infinitesimally small cost rate. It is the optimal strategy for an infinitesimally small cost rate. It has been found theoretically in a preceding work.
As shown in the learning history below, the no-transaction band quickly learns to hedge. While an ordinary feed-forward network struggles even after 1,000 times of simulations, the no-transaction band reaches its minimum in around 50 times. Preferred Networks’ MN-2 supercomputer completes it in seconds, which we expect is sufficiently quick for practical applications.

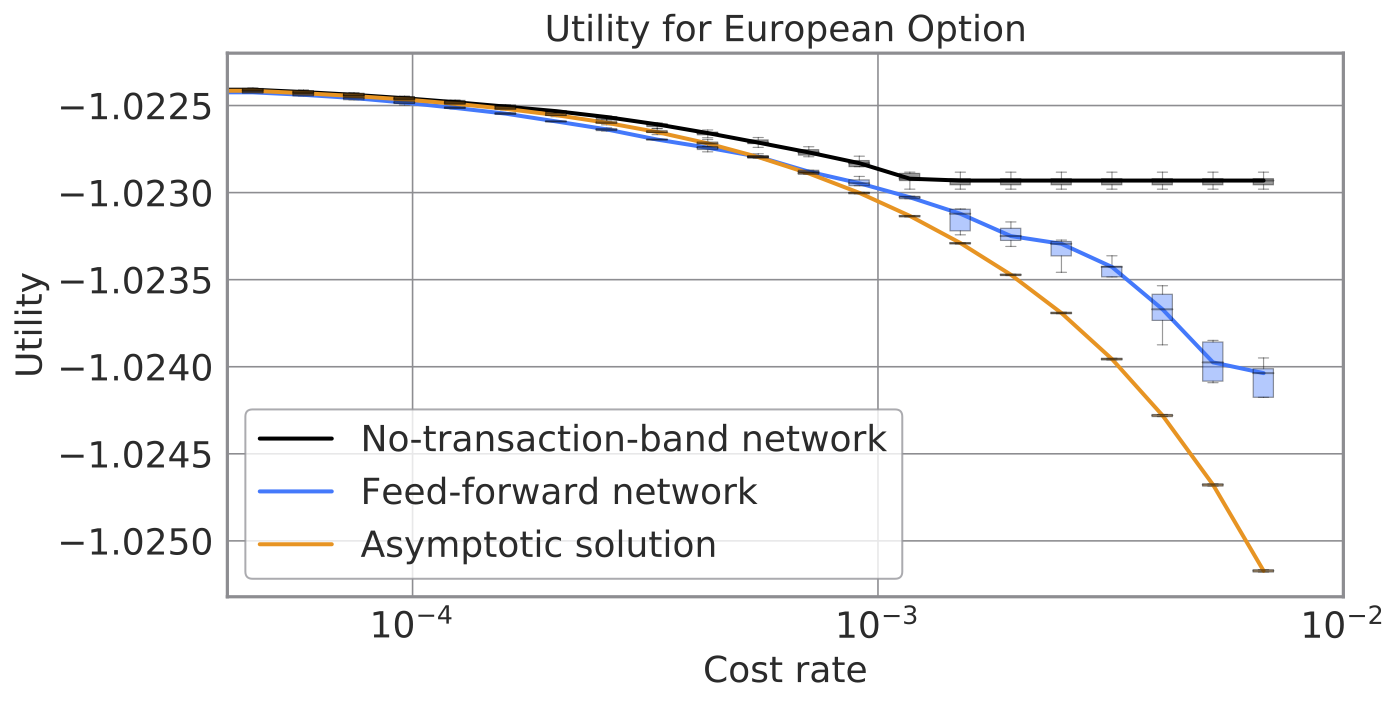
The figure below presents the expected utility attained by each method as a function of a cost rate. The no-transaction band achieves the highest utility for a wide range of costs. It is worth mentioning that the utility of the no-transaction band network bottoms at some value of cost. That is because the no-transaction band learns “not to hedge” when a transaction cost is too expensive. This advantage is distinctive from the other two.
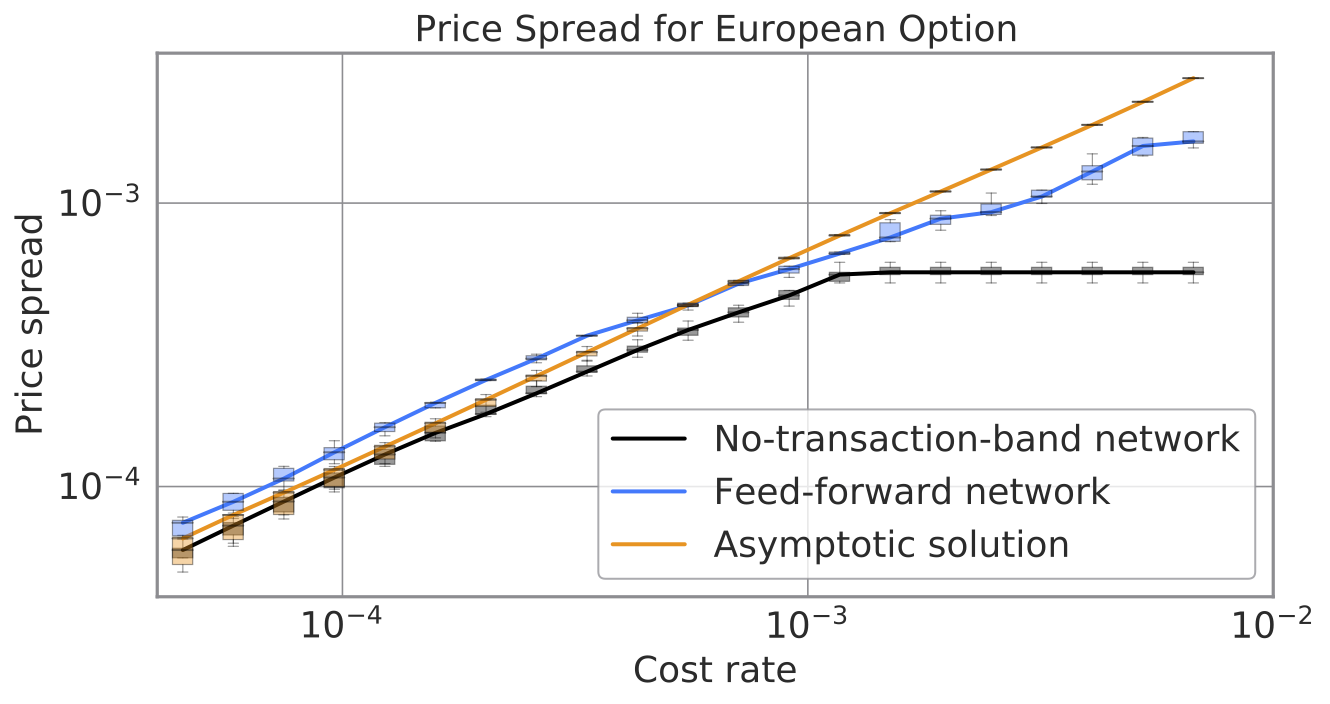
We computed derivative prices as well. Let us omit the pricing theory here and emphasize that a lower price is better for competitive brokerage businesses. The no-transaction band network attains prices up to several percent lower than the other methods. This discount is nothing but the value added to the security companies and their counterparties. Besides, tighter quotes provide liquidity to the derivative market.
Let us remark why the no-transaction band network achieves lower prices than the “analytic” asymptotic solution. Our interpretation is that while the analytic solution approximates by truncating sub-leading orders for a cost rate, the no-transaction band takes account of the higher-order contribution. Also, the price computed by the no-transaction band is the most accurate since the definition of the price considered here is the minimum value among all possible hedging strategies.
The no-transaction band quickly learns to hedge a lookback option as well. Surprisingly, the no-transaction band network achieves its optima as fast as the European option, even though the lookback option bears extra complications of path dependence and needs more inputs. This result suggests that our method would scale for more input features.

Achievements
We presented our study as “Neural Network Architecture for Efficient Deep Hedging” (in Japanese) and had the privilege to receive the Incentive Award of the Japanese Society of Artificial Intelligence. Also, we released a detailed paper, “No-Transaction Band Network: A Neural Network Architecture for Efficient Deep Hedging” (in English).
We provide minimal implementation to experience the efficiency of the no-transaction-band network in a GitHub repository: pfnet-research/NoTransactionBandNetwork.
We also released PFHedge, which is a PyTorch-based library for Deep Hedging. One can try out Deep Hedging with a code as simple as follows. We hope this library accelerates the research of Deep Hedging toward data-driven derivative business.
from pfhedge.instruments import BrownianStock, EuropeanOption from pfhedge.nn import Hedger from pfhedge.nn import MultiLayerPerceptron derivative = EuropeanOption(BrownianStock(cost=1e-3)) hedger = Hedger(MultiLayerPerceptron(), inputs=["moneyness", "expiry_time", "prev_hedge"]) hedger.fit(derivative) hedger.price(derivative)
Conclusion
The no-transaction band network learns the optimal hedging strategy blazingly fast. It enables securities companies to meet their customers’ needs with quicker and tighter quotes while slashing operational costs. Also, a cost-efficient hedging strategy can handle high-volume orders and supply liquidity to the derivative market. While there are still practical challenges ahead of Deep Hedging, we are proud to have overcome one of the most challenging obstacles to lead technology-driven innovation in the financial industry.
We proposed the no-transaction band network by extending traditional research in quantitative finance to overcome the inherent problems of deep learning. It was a valuable experience for me to learn that exceptional ideas are inspired by leveraging different perspectives.
Collaborators’ generous mentoring and Preferred Networks’ abundant computing resources enabled these all achievements. Imos-san (Imajo-san) has proactively shared ingenious ideas to make the way out of challenging situations. Ito-san has shared a lot of expertise about quantitative finance, which was fresh for me. Minami-san has been so dependable when it comes to analytical approaches to the optimal control problem and vigorous and concise writing of the paper. Nakagawa-san at Nomura Asset Management has contributed both theoretical and practical issues in the financial market, which will be essential to look ahead of applications. Also, Preferred Networks’ supercomputer has been indispensable for research with a lot of trials. Let me conclude this article by expressing my great appreciation for Preferred Networks and Nomura Asset Management.
References
- Shota Imaki, Kentaro Imajo, Katsuya Ito, Kentaro Minami and Kei Nakagawa, “No-Transaction Band Network: A Neural Network Architecture for Efficient Deep Hedging”. arXiv:2103.01775 [q-fin.CP], Available at SSRN: https://ssrn.com/abstract=3797564
- Shota Imaki, Kentaro Imajo, Katsuya Ito, Kentaro Minami, Kei Nakagawa, “Neural Network Architecture for Efficient Deep Hedging“, JSAI Special Interest Group of Financial Informatics 26th conference.
- Hans Bühler, Lukas Gonon, Josef Teichmann and Ben Wood, “Deep hedging”. Quantitative Finance, 2019, 19, 1271–1291. arXiv:1802.03042 [q-fin.CP].




