Blog
Japanese blog available here.
As there was a press release about the establishment of a joint venture last month, we are conducting research on materials fields as well.
This time, we released a pytorch implementation of the algorithm called DFT Dispersion. In this blog, we will introduce DFT Dispersion and why we implemented it in pytorch.
In short
In new material development fields, a chemical computation method called DFT is used to perform simulations at the atomic scale. DFT Dispersion is a dispersion force correction term added to the energy obtained by the DFT. By adding this, it is possible to simulate the target system with greater accuracy. It is possible to calculate faster by utilizing the GPU, which is achieved by implementing with PyTorch. For more information on why you wanted to speed it up, please refer to “The Significance of Speedup”.
DFT
If you want to simulate phenomena that occur at an atomic scale, quantum mechanics theory is necessary to obtain energy by taking into account the electronic state. For steady state, the Schrodinger equation given below determines the wave function \(\Psi\) (representing the electronic state) and energy \(E\).
\[ \left( – \frac{\hbar^2}{2m} \nabla^2 + V(\boldsymbol{r}) \right) \Psi (\boldsymbol{r}) = E \Psi (\boldsymbol{r}) \]
However, it is known that this Schrodinger equation is very difficult to solve. An exact solution can be obtained only for hydrogen atoms, and cannot be obtained when two or more electrons exist.
DFT stands for Density Functional Theory, the Schrodinger equation described above can be solved in realistic time under a certain approximation with this technique.
DFT Dispersion
DFT is a method of solving Schrodinger equations “under a certain approximation”. However, some long-range interactions are difficult to handle under the approximation of DFT. The dispersion force (or Van der Waals force) is a long-range interaction that cannot be fully described in standard DFT methods. It influences the accurate simulation of molecule systems (*1 ).
*1: There are currently some DFT methods that take into account dispersion, and are explained in detail in the slides of “The Latest Chemical Theory Based on Density Functional Method”.
The dispersion force is the force generated by the interaction of an induced dipole with another charge at a distance. Please refer to this article for more details.
The most famous method in DFT dispersion is called DFTD3 [1, 2] (*2). The DFTD3 method is very light compared to DFT, and it is easy to obtain good results when used together with DFT. Thus this method is widely used in software such as VASP and ASE. The DFTD3 paper itself has 18285 citations as of May 2021.
※2: DFTD4 [3, 4, 5], an improved version of DFTD3, is also proposed. However, we implemented DFTD3 this time, which is widely used in physical and chemical areas as a stable version.
The main dispersion interaction is expressed as \(r^{-6}\) and \(r^{-8}\) terms in DFTD3. The \(r^{-6}\) term comes from the interaction between permanent and induced dipoles, and the \(r^{-8}\) comes from the interaction of permanent dipoles and induced quadrupoles. It is basically a two-body interaction formula.
\[ E_{\mathrm{disp}} = – \frac{1}{2} \sum_{A \ne B} \sum_{n = 6,8} s_n \frac{C_n^{AB}}{r_{AB}^{n}} \]
\(r_{AB}\) is the distance of atoms between A & B. \(s_n\) is a fitting parameter determined by each exchange-correlation functional. \(C_n^{AB}\) coefficient is calculated from the results of the prior physical computation and the coordination number of atoms A, B)
\[ E_{\mathrm{DFT-D3}} = E_{\mathrm{DFT}} + E_{\mathrm{disp}} \]
The total energy with DFTD3 is calculated from the dispersion force correction energy \(E_{\mathrm{disp}}\) and the energy \(E_{\mathrm{DFT}}\) obtained by the DFT calculation.
\[ E_{\mathrm{DFT-D3}} = E_{\mathrm{DFT}} + E_{\mathrm{disp}} \]
[1] A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu
[2] Effect of the damping function in dispersion corrected density functional theory
[3] Extension of the D3 dispersion coefficient model
[4] A generally applicable atomic-charge dependent London dispersion correction
[5] Extension and evaluation of the D4 London-dispersion model for periodic systems
Advantage of pytorch implementation
The implementation of DFTD3 is published by the author. There are the following reasons for reimplementing this time.
Auto-differentiation
If you implement it using a deep learning framework such as PyTorch, you can take advantage of automatic differentiation and make it easier to implement. Specifically, by implementing only the equation for energy, it is possible to calculate the force and the virials used in the calculation of pressure (in the case of periodic systems).
\[ F_{i} = – \frac{\partial E}{ \partial r_i } \]
In addition, implementing it as a function on pytorch will make it easier for future applications such as learning in conjunction with other Neural Networks.
Speedup
This is the main purpose. Calculations can be performed on both CPU and GPU by implementing it on pytorch.
If we look at the formula of DFTD3 above, we can see that similar interactions are calculated for so many pairs of two bodies and it is easy to increase parallelism. These formulas can benefit from GPU parallelization. As a result, you can expect faster speed by using a GPU.
Results
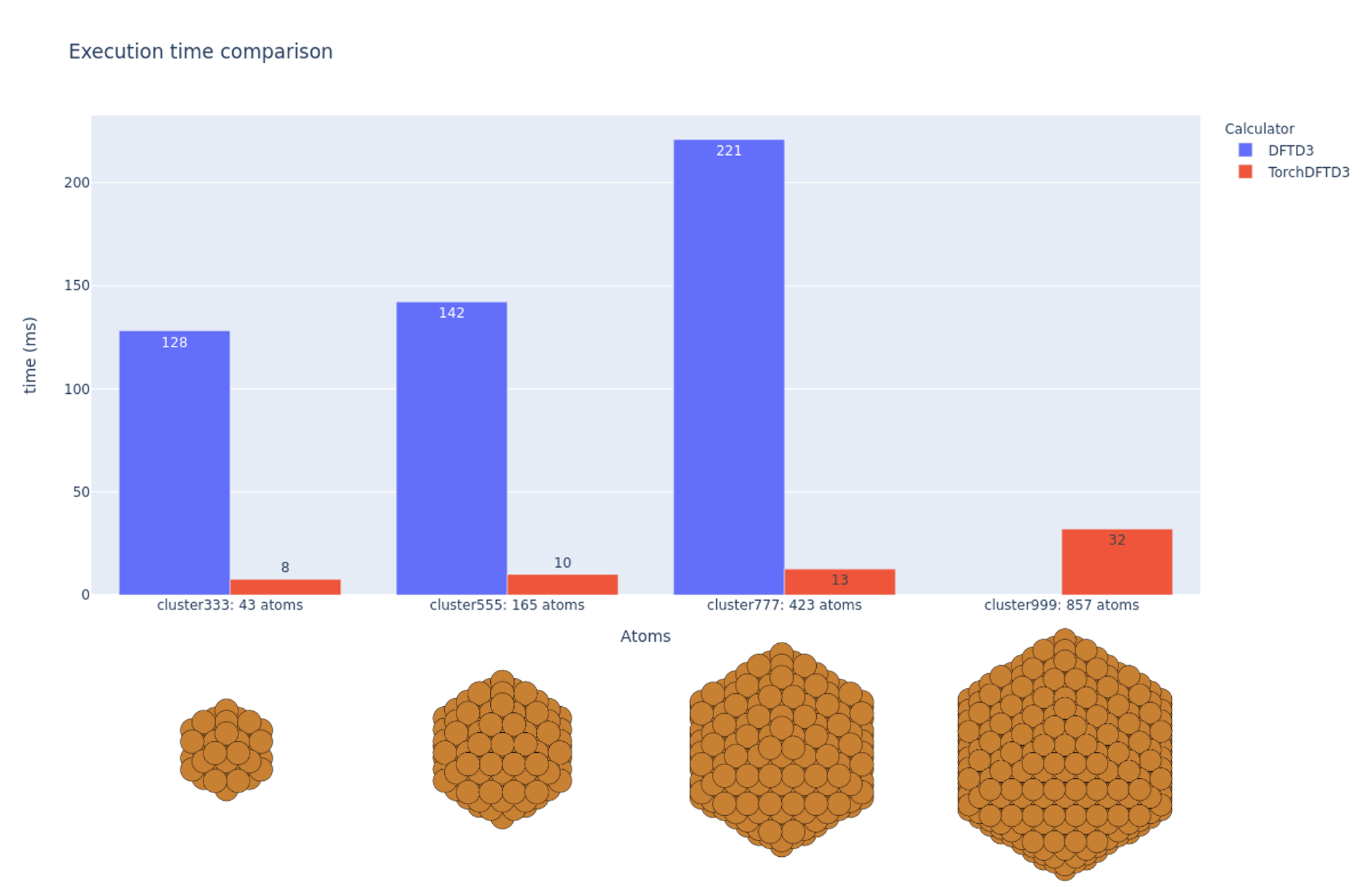
We prepared cluster atoms with size 43, 165, 423 and 857, and measured calculation time.
Even in the dftd3 implementation of the use of CPU, it works fast at hundreds ms, but TorchDFTD3 using GPU (this implementation) computes tens of ms and even more than 10 times faster.
* Note that it depends on the CPU/GPU spec environment, so it is a rough comparison only.
Measured environments
- CPU Intel(R) Xeon(R) Gold 6254 CPU @ 3.10GHz
- GPU Tesla V100
- Only measured with non-periodic system
The code is available on github, please try!
github: https://github.com/pfnet-research/torch-dftd
The Significance of Speedup
DFTD3 is originally proposed to correct the results of DFT calculations. If you have ever been involved in this field, you may notice that DFT is a heavy calculation that can take hours to months depending on the size of the target system, whereas DFTD3 is a ms order to calculate.
DFT calculation is a bottleneck when used as-is, and there is no need to speed up DFTD3.
However, in recent years, a technology called Neural Network Potential (NNP) has been developing, and the energy of DFT calculation results can be predicted in ms order by Neural Network. We can now consider calculating energy such as NNP prediction+DFTD3. In that case, both can be calculated in ms order, so the significance of speeding up DFTD3 comes out.
By speeding up both NNP and DFTD3, DFT energy predictions with dispersion correction can be calculated extremely fast. Molecular Dynamics methods which require more than 10^6~ repeated energy calculation will be possible.
Related to this topic, the following research using NNP was conducted during the 2020 internship.
We are hiring!
We are hiring researchers and engineers to tackle state-of-the-art research and development topics to accelerate our material search business.
We are also looking for engineers to advance product development to provide these technologies to customers as a service!
- Resarch
- Chem Researcher
- Engineering
- Chem Engineer
- Web Application Engineer
- ML Backend Engineer
- Site Reliability Engineer