新材料開発などの分野では、原子レベルのスケールでシミュレーションを行うためにDFTという化学計算手法が使われます。DFT Dispersionとは、そのDFTで得られるエネルギーに対して加える、分散力補正項のことで、これを加えることによりさらに精度良く対象とする系をシミュレーションできることがあります。今回、pytorch実装をしたことでGPUを活用することができ、より高速に計算ができるようになりました。なぜ高速化したかったのか、に関しては “高速化する意義” をご参照ください。

DFT とは

原子レベルのミクロなスケールで起こる現象をシミュレーションしたい場合、その電子状態まで考慮してエネルギーなどを求めるには量子力学の理論が必要となります。定常状態の場合、以下で与えられるSchrodinger 方程式によって、電子状態を表す波動関数 \(\Psi\) およびエネルギー \(E\) が求まります。

\[ \left( – \frac{\hbar^2}{2m} \nabla^2 + V(\boldsymbol{r}) \right) \Psi (\boldsymbol{r}) = E \Psi (\boldsymbol{r}) \]

しかし、このSchrodinger方程式は解くのが非常に難しく、唯一水素原子についてのみ厳密解を得ることができ、電子が２つ以上になると厳密な解は得られないことが知られています。

DFTとはDensity Functional Theory（密度汎関数法）の略で、上記のSchrodinger 方程式をある一定の近似の元で現実的な時間で解けるようにしている手法です。

DFT Dispersion とは

DFTは “ある一定の近似のもとで” Schrodinger 方程式を解く手法でした。その近似の中で扱うことが困難になってしまっているものとして長距離間で働く相互作用があり、その中でも実用上重要なものに分散力/Van der Waals 力というものがあります(※1)。

※1: 現在DFTの手法・基底のなかには分散力まで考慮したものも出てきています、「密度汎関数法にもとづく最新の化学理論」のスライドなどで詳しく解説されています。

http://www2.riken.jp/qcl/members/tsuneda/web/dft05-sec3.pdf

分散力というのは、電子状態が誘起することによって生じる双極子が遠くの別の電荷と起こす相互作用によって生じる力です。より詳しくはこちらの記事などをご参照ください。

DFT Dispersionの中でも有名なのはDFTD3 [1, 2] と呼ばれる手法です(※2)。この手法自体の計算はDFTと比べて大変軽く、DFT計算結果に加えて使用することで良い結果が得られやすいことから、広く使われており、VASPやase といったソフトウェアにも標準実装されています。DFTD3 論文自体は2021年5月現在 18285 citaton されています。

※2: 現在DFTD3の改良版であるDFTD4 [3, 4, 5] も提案されていますが、今回は安定版として広く物理・化学界隈で使われているDFTD3を実装しました。

DFTD3 のメインとなる項は以下の式で示すように、永久双極子と誘起双極子の相互作用からくる \(r^{-6}\) や永久双極子と誘起四重極子の相互作用からくる \(r^{-8}\) で表されるような２体相互作用の式となっています。

\[ E_{\mathrm{disp}} = – \frac{1}{2} \sum_{A \ne B} \sum_{n = 6,8} s_n \frac{C_n^{AB}}{r_{AB}^{n}} \]

(\(r_{AB}\) が原子A, Bの距離、\(s_n\) は交換相関汎関数ごとに決められているFitting parameter、\(C_n^{AB}\)は事前の物理計算の結果と原子A, Bの配位数から計算される係数です)

これにより得られた分散力補正エネルギー \(E_{\mathrm{disp}}\) と、 DFTによる計算で得られたエネルギー \(E_{\mathrm{DFT}}\) から、DFTD3 によるエネルギーが計算されます。

\[ E_{\mathrm{DFT-D3}} = E_{\mathrm{DFT}} + E_{\mathrm{disp}} \]

[1] A consistent and accurate ab initio parametrization of density functional dispersion correction (DFT-D) for the 94 elements H-Pu
[2] Effect of the damping function in dispersion corrected density functional theory
[3] Extension of the D3 dispersion coefficient model
[4] A generally applicable atomic-charge dependent London dispersion correction
[5] Extension and evaluation of the D4 London-dispersion model for periodic systems

pytorch 実装によるメリット

DFTD3 の実装は著者が公開をしています。今回再実装を行ったのには以下のような理由があります。

自動微分の活用

pytorchなどのDeep learning frameworkを用いて実装をすると、自動微分を活用することができ実装が簡単になります。具体的には、エネルギーの計算式だけ実装することで、その微分値である力 (Force) や, 圧力の計算に使われるビリアル(周期系の場合)が計算できます。

\[ F_{i} = – \frac{\partial E}{ \partial r_i } \]

また、pytorch 上の関数として実装しておくことで、将来、他のNeural Network と組み合わせて学習を行うといった応用も容易になります。

高速化

こちらが今回の１番の目的となります。pytorch上での実装を行うことで、CPU/GPU などさまざまなデバイスで計算を行うことができるようになります。

上記DFTD3 の計算式を見てみると、とてもたくさんの２体ペアに対して似たような相互作用を計算していて、並列性をとても高めやすい式となっているのがわかります。こういった式はGPU による並列化の恩恵が出やすい計算となります。結果、GPUを用いることで高速化が期待できます。

結果

43原子、165原子、423原子、857原子と大きさを変えたClusterを用意して計算時間を測定したものが以下の図となります。CPUを利用したaseのDFTD3 実装でも数百 ms と高速に動作しますが、GPUを利用したTorchDFTD3 (今回の実装)では、数十 ms とさらに10倍以上高速に計算できることがわかりました。（CPU/GPUのスペック・環境にもよるため、あくまで大まかな比較です）

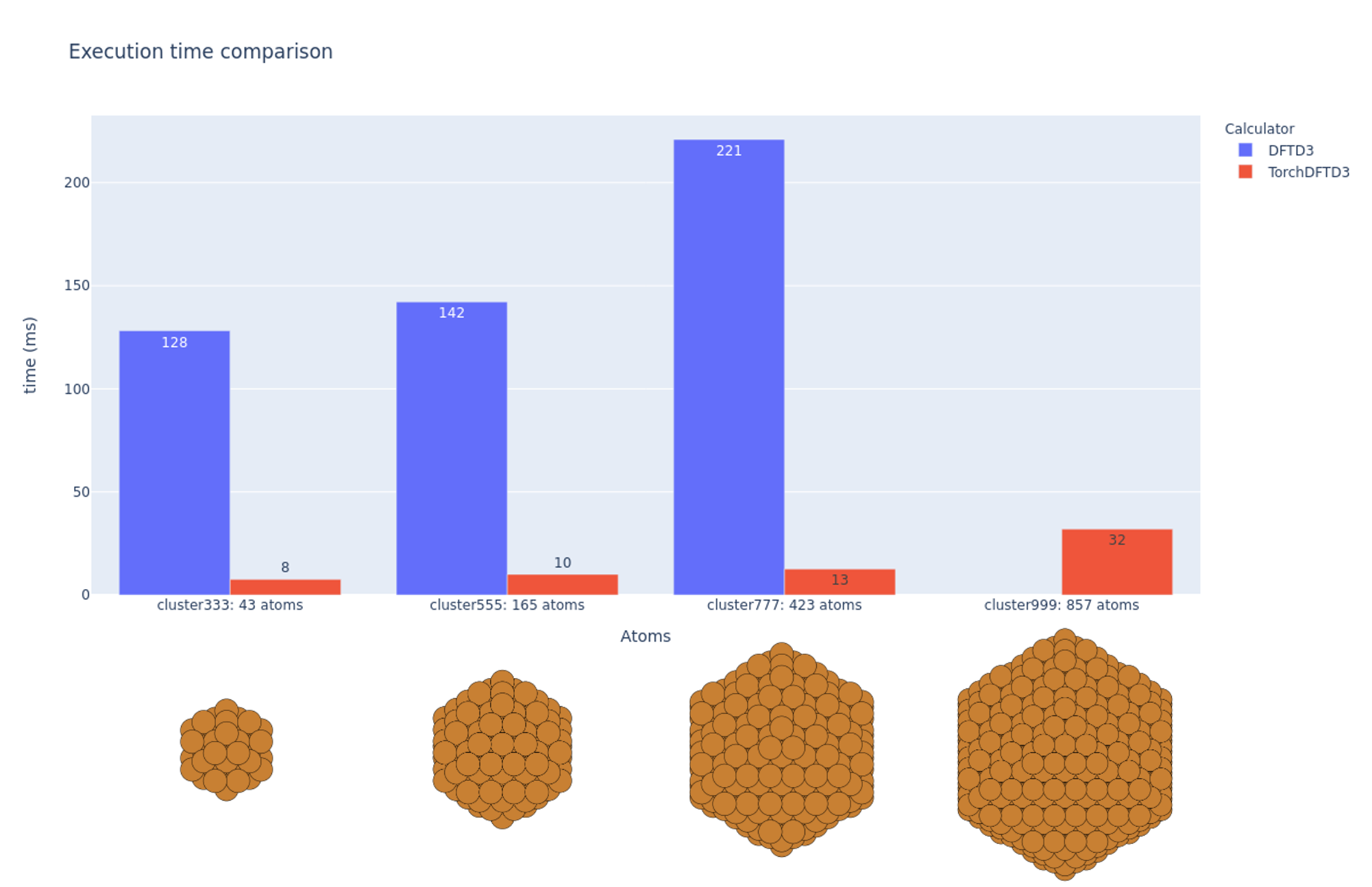
計測条件

CPU Intel(R) Xeon(R) Gold 6254 CPU @ 3.10GHz
GPU Tesla V100
今回は周期境界条件OFFでのみ測定

実装は以下で公開されています。ぜひ試してみてください！

github: https://github.com/pfnet-research/torch-dftd

高速化する意義

DFTD3 はもともとDFTの計算結果を補正するために行うものとして提案されました。この分野に関わったことのある方はお気づきかと思いますが、DFTは対象系のサイズによって数時間〜数ヶ月かかるようなこともあるくらい重い計算であるのに対し、DFTD3 はms オーダーで計算が終わります。

そのまま使う場合にはDFT計算の方がボトルネックになっており、DFTD3 を高速化する必要はありません。

しかし近年、ニューラルネットワークポテンシャル (Neural Network Potential, NNP) と呼ばれる技術が発展してきており、DFTのエネルギー計算結果をNeural Networkによって ms オーダーで予測できるようになってきました。NNPを活用することで、NNP予測 + DFTD3 といったエネルギーの計算ができるようになり、その場合はどちらもms オーダーでの計算が可能となるためDFTD3 を高速化する意義が出てきます。

NNPおよびDFTD3 の双方を高速化することで、分散力補正の入ったDFT エネルギー予測が極めて高速に計算できるようになり、エネルギー計算を10^6~ 以上繰り返す必要があるような分子動力学法 (Molecular Dynamics, MD) などへの適用も視野に入ってきます。

ちなみに、2020年インターンシップではNNPを用いた以下のような研究が行われていました。