Blog

Home
Blog
Optunaで始めるハイパーパラメータ最適化

2023.02.02

Optunaで始めるハイパーパラメータ最適化

Area

Data Science / AutoML

Tag

# Optuna

Toshihiko Yanase

この記事は、電気情報通信学会会誌に寄稿した解説記事「Optunaで始めるハイパパラメータ最適化」の転載です。この記事のパワーアップ版ともいえる書籍「Optunaによるブラックボックス最適化」が2月21日に出版されます。Optuna開発チームのメンバーが、Optunaについてより詳しく、よりわかりやすく説明し、より豊富な事例を紹介していますので、ぜひ予約して発売日からお読みください！

出典
柳瀬利彦, Optunaで始めるハイパパラメータ最適化, 電子情報通信学会誌　Vol.104 No.7 pp.728-733 2021年7月 ©電子情報通信学会2021

Abstract

機械学習アルゴリズムの性能を引き出すためには，ハイパパラメータをデータやタスクに応じて適切に調整する必要がある．本稿では，その自動的な調整のためのツールとして，オープンソースのハイパパラメータ最適化フレームワークであるOptunaを紹介する．まず，最適化の手法を概説し，コード例を交えて具体的な最適化の方法を説明する．そして，実問題における事例を音声認識とロボットの設計の2つについて紹介し，多様な分野でハイパパラメータ最適化が応用されていることを示す．

1．はじめに

多くの機械学習アルゴリズムは，データから求まるパラメータのほかに，利用者があらかじめ定めておくハイパパラメータを持つ．例えば，ニューラルネットを確率的勾配法で訓練する場合，各ユニットの重みは前者であり，学習率は後者に相当する．近年，機械学習モデルのハイパパラメータが訓練に与える影響を様々なデータセットにより網羅的に調査した結果が報告されており[1]，ハイパパラメータの調整の重要性が注目されつつある．

しかし，ハイパパラメータは，実際にモデルの訓練と評価をしてみないとその良し悪しが分からないという問題がある．つまり，最適化においてはハイパパラメータの入力と評価を何度も繰り返す必要がある．そこで，こうした試行錯誤を代替するハイパパラメータ最適化[2]のためのソフトウェアが登場している．

本稿では，ハイパパラメータ最適化ソフトウェアの一つであるOptunaを題材に，ハイパパラメータの最適化の方法をコード例や応用事例を交えて説明する．また，ハイパパラメータ最適化の手法は，機械学習以外の分野でも応用されている．この事例として，音声認識とロボットハンドの設計パラメータの最適化の事例を紹介する．

2．ハイパパラメータの最適化手法

2．では，ハイパパラメータの最適化手法を概説する．ただし，各手法のアイデアのみを説明し詳細には立ち入らないため，詳しくは尾崎らによるサーベイ論文[3]などを参照されたい．

2.1　ブラックボックス最適化としてのハイパパラメータ最適化

ハイパパラメータの最適化は，ブラックボックス最適化として扱うことができる．ブラックボックス最適化では，入力値とそれに対応する目的関数の値のみを使って最適化を行う．機械学習の場合，ハイパパラメータの値がブラックボックス関数の入力であり，訓練と評価の結果が出力となる．

図1にブラックボックス最適化の代表的な手法である，グリッドサーチ，ランダムサーチ，ベイズ最適化の探索の様子を示す．

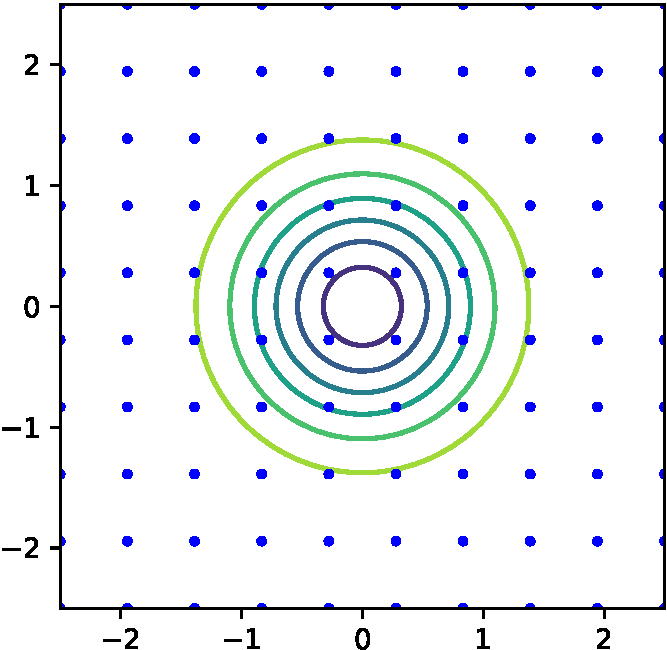(a) 探索空間	(b) グリッドサーチ
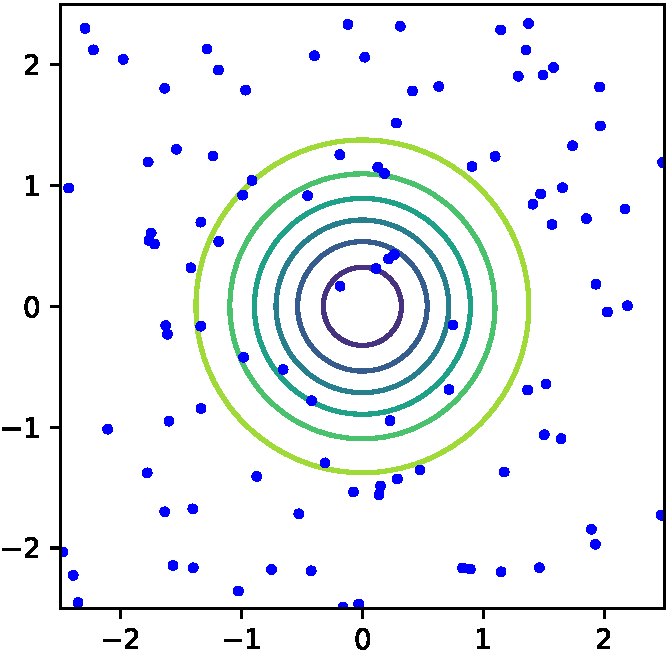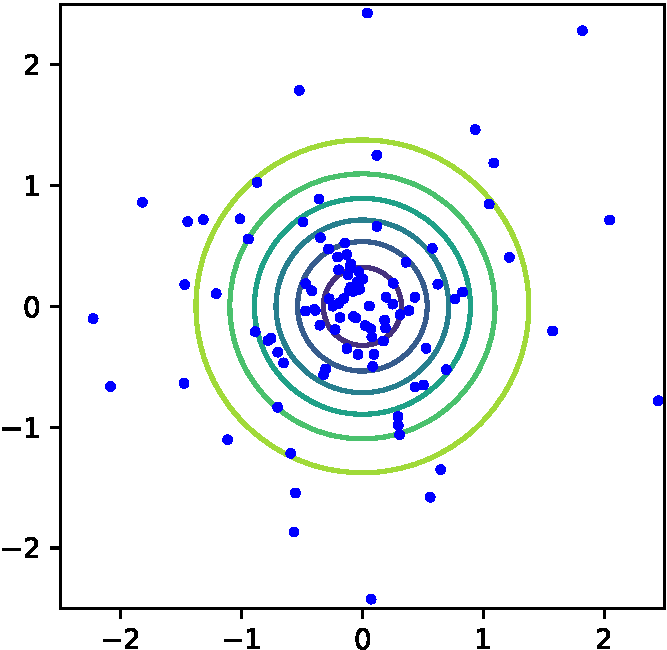(c) ランダムサーチ	(d) ベイズ最適化: TPE

図１探索空間と各種探索手法によるサンプル点

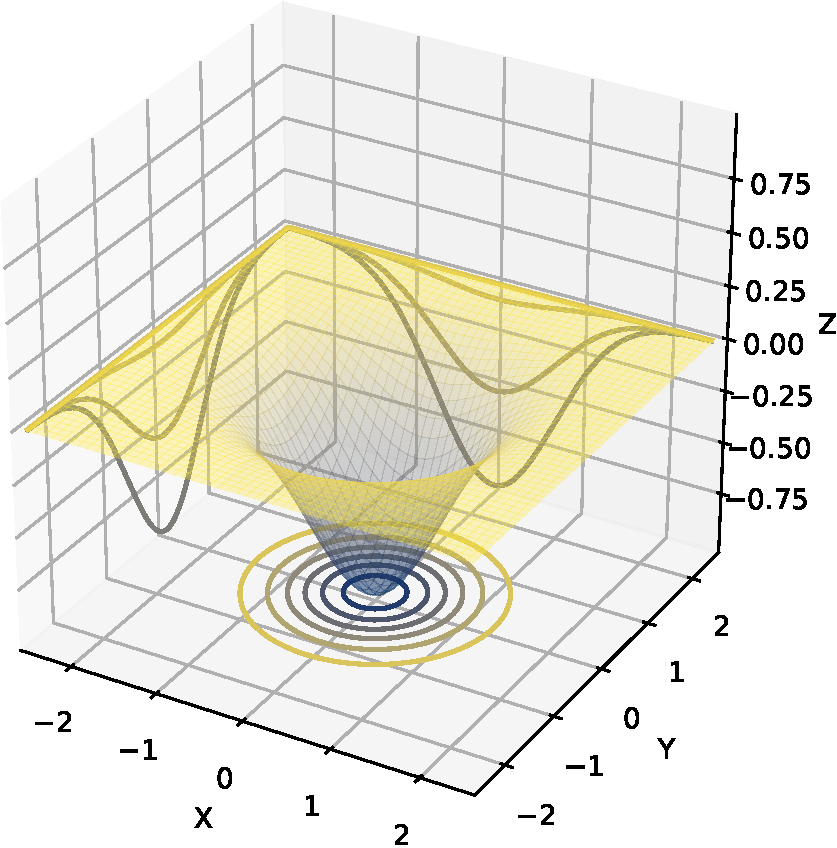
図1(a)にはシンプルな単峰性の目的関数の等高線プロットを示す．\(x, y\)の２つの入力変数があり，その定義域は\([-2.5, 2.5]\)である．最適値は\(x=y=0\)でとり，その値は\(0\)である．

グリッドサーチは，各ハイパパラメータに対して代表点を選択し，その全組み合わせを探索する．この例では，図1(b)に示すように\(x\)と\(y\)それぞれ10点等間隔に代表点を定めた．グリッドサーチは実装の容易さと探索の網羅性からよく使われる方法である．

次に，ランダムサーチでは，各ハイパーパラメタの値を乱数によって決定する．図1(c)には一様乱数による100点のランダムサーチの探索点の例を示す．ランダムサーチも実装が容易であり，無作為に探索できることからよく使われる方法である．

ベイズ最適化ではこれまでの探索履歴を用いて，より効率的な探索を図る．図1(d)にベイズ最適化の一手法であるTree-structured Parzen Estimator (TPE) [4]の探索点の例を示す．前記二つの手法と異なり，最適値付近に点が集中している様子が見られる．ベイズ最適化では，未探索の領域と探索済みの有望な領域をバランスよく探索するため，グリッドサーチやランダムサーチと比べてより少ない試行回数でより良いハイパパラメータの発見を期待することができる．なお，TPEでは探索履歴の活用にカーネル密度推定を用いていたが，ベイズ最適化ではそのほかにも，ガウス過程を用いる手法[5]，ランダムフォレストを用いる手法[6]など様々な手法が提案されている．

2.2 機械学習の性質を考慮した最適化

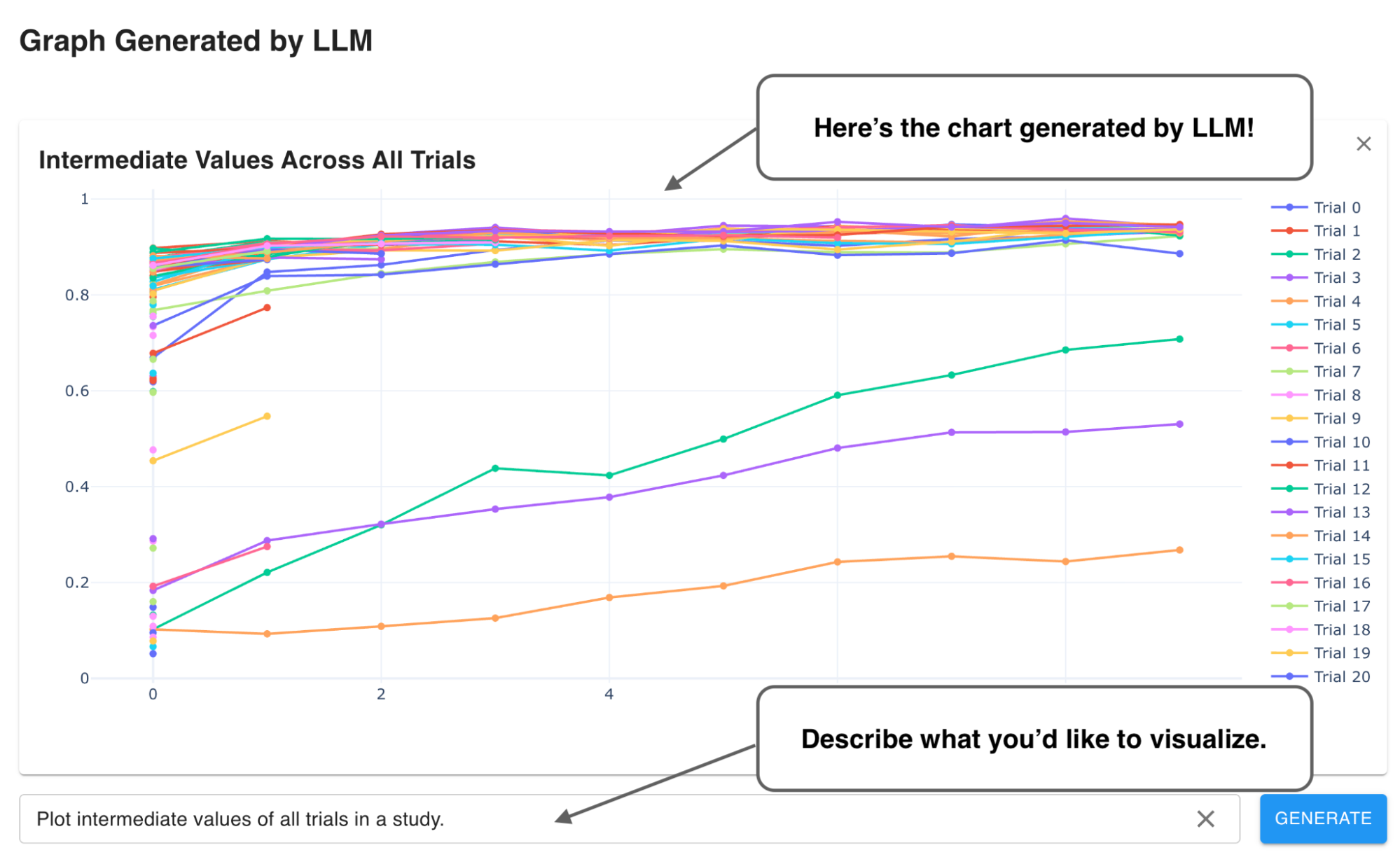
機械学習のハイパパラメータ最適化は，完全なブラックボックス関数ではない場合もある．例えば，ニューラルネットワークの確率的勾配法による反復的な訓練では，エポックごとに中間評価値を得ることができる．こうした特性を生かした最適化の工夫にアーリーストッピングがある．アーリーストッピングでは，ほかの試行と比較することにより見込みの薄い試行の訓練を途中で打ち切ることで，最適化時間の短縮を図る．

図2に早期終了の様子を示す．横軸がエポック，縦軸がクロスエントロピー損を表す．緑の線が100エポックまで完了した試行，その他がアーリーストッピングした試行である．性能の悪い試行ほど早いエポックで訓練が打ち切られており，打切り後のエポック数分だけ最適化時間を短縮できている．具体的な手法としては，Successive Halving[7]やその拡張であるHyperband[8]などがある．

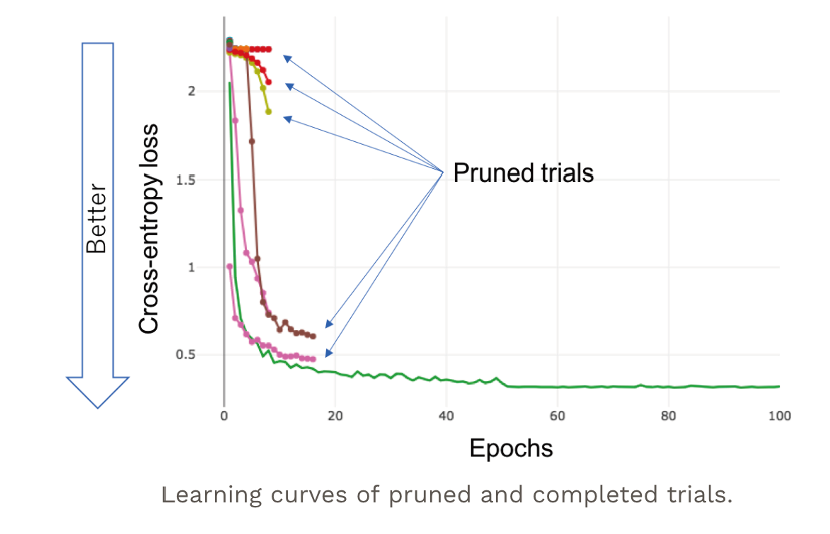
図２アーリーストッピングの例．性能の悪い試行ほど早いエポックで訓練が打ち切られている．

3．ハイパパラメータ最適化ライブラリOptuna

ハイパパラメータ最適化ライブラリのOptunaを用いると，２．で説明したハイパパラメータの最適化を容易に実装できる．以下では，Optunaの5つの特徴「プラットホーム非依存」，「条件分岐等の制御構造サポート」，「並列化の容易性」，「効率的な最適化アルゴリズム」，「可視化機能」をコード例を交えて説明する．

3.1 プラットホーム非依存

OptunaはPythonが使える環境であれば pip install optuna コマンドを実行するだけで利用可能になる．また利用法もシンプルであり，図３のようなPythonスクリプトを書き，実行するだけでよい．図３では，簡単な二次関数の最小化を行っている．目的関数は\((x – 2)^2\) ，\(x \in [-10, 10]\)であり，3行目から5行目で定義されるobjective関数に記述されている．4行目で\(x\)の値をサンプルし，5行目で目的関数の値を返している．この1回の目的関数の評価が試行(trial)であり，objective関数の引数のtrialオブジェクトは1回の目的関数評価を管理するために使われる．7行目で作成しているstudyオブジェクトは，一連のtrialを管理する．8行目では，studyにobjective関数を指定して，100 trialの最適化を実行している．

最後に9行目で最適だったtrialを表示している．以上のように9行のコードだけで簡単に最適化を実行できる．

import optuna

def objective(trial):
    x = trial.suggest_float("x", -10, 10)
    return (x - 2) ** 2

study = optuna.create_study()
study.optmize(objective, n_trials=100)
print(study.best_trial)

図３二次関数の最小化のコード例　目的関数\((x-2)^2\)を\(x \in [-10, 10]\)の範囲で探索している

3.2 条件分岐等の制御構造サポート

より実践的な例では，ハイパパラメータの値によって場合分けや繰り返しを記述したいことがある．そのような場合，OptunaはPythonの構文を使って記述することができる．図４に機械学習モデルのハイパパラメータの最適化のコード例を示す．この例では，サポートベクターマシンによる分類器(SVC)とRandomForestsのモデルの選択と，それぞれのモデルのハイパパラメータを最適化している．なお，目的関数の評価値はAccuracyであり，図３とは異なり最大化を行いたいため，studyを作る際にdirection=”maximize”を指定している．

SVCとRandomForestsではハイパパラメータが異なるため，8行目でモデルの種類を表すcls_nameによって条件分岐し，9行目ではSVCのハイパパラメータを，12行目ではRandomForestsのハイパパラメータをそれぞれサンプルしている．このように，ある特定の状況のみで有効になるハイパパラメータについてもOptunaを使えば直観的に記述できる．

 
def objective(trial):
    # データセットのロード
    iris = sklearn.datasets.load_iris()
    x, y = iris.data, iris.target

    # ハイパパラメータのサンプリング
    cls_name = trial.suggest_categorical("classifier", ["SVC", "RandomForest"])
    if cls_name == "SVC":
        svc_c = trial.suggest_float("svc_c", 1e-10, 1e10, log=True)
        cls = SVC(C=svc_c, gamma="auto")
    else:
        d = trial.suggest_int("max_depth", 2, 32)
        cls = RandomForestClassifier(max_depth=d)

    # 評価値の計算
    score = cross_val_score(cls, x, y)
    return score.mean()

study = optuna.create_study(direction="maximize")
study.optimize(objective, n_trials=100)

図４機械学習モデルのハイパーパラメータの最適化のコード例　終了した段階で，load_studyをしてstudy.best_trialを取得すれば，最適化全体で最も性能が良かったtrialを得ることができる．

3.3 並列化の容易性

機械学習モデルの訓練には時間がかかる場合も多い．Optunaを使えば容易にハイパパラメータ最適化を並列化してワークフロー全体を高速化することができる．並列化のためには，最適化履歴を永続化する必要があり，ここではリレーショナルデータベース（RDB）を用いる．

図５と図６に並列化のためのコード例を示す．図５では，これまでと違いcreate_studyではなくload_studyをしている．これは既にRDBに保存されているstudyをその名前study_nameとRDBのURLであるstorageをもとに読み出している．図６ではstudy_nameとstorageを指定してstudyを作り，続けて図５のスクリプトを複数実行している．複数実行した図５のジョブは，並列にRDBにアクセスし最適化を実行する．並列に実行した全てのジョブが終了した段階で，load_studyをしてstudy.best_trialを取得すれば，最適化全体で最も性能が良かったtrialを得ることができる．

 
study = optuna.load_study(
    study_name="parallel-study",
    storage="sqlite:///sample.db")
study.optimize(objective)

図５並列化の例 (run.py)

 
$ optuna create-study --storage "sqlite:///sample.db" --study-name="parallel-study"
$ python run.py
$ python run.py

図６並列化の例 (Shell)

3.4 効率的な最適化アルゴリズム

Optunaは，２．で説明したランダムサーチやベイズ最適化，更にはCMA-ESなど様々な最適化手法をサポートしている．そうした最適化手法はsamplerとして実装されており，optuna.create_studyのsampler引数により切り替えることができる．

また，同じく２．で説明した早期終了はOptunaではprunerとして実装されており，samplerと同様にprunerはoptuna.create_studyのpruner引数で指定できる．早期終了を利用するには，中間評価値の報告と早期終了の判定をobjective関数に追加すればよく，そのコード例を図７に示す．5行目からのforループで，線形モデルを確率的勾配法で訓練している．6行目で1エポック分のパラメタ更新をし，9行目でそのエポックでの評価値をtrialに報告している．12行目では早期終了の判定をしており，もし終了と判定されれば13行目で例外を発生させる．なお，各機械学習ライブラリ向けのコールバック関数を使えばさらに変更点は少なくなる．

 
def objective(trial):
    alpha = trial.suggest_float("alpha", 1e-5, 1e-1, log=True)
    clf = sklearn.linear_model.SGDClassifier(alpha=alpha)

    for step in range(100):
        clf.partial_fit(train_x, train_y, classes=classes, )

    # 現時点での評価値を報告
    trial.report(clf.score(valid_x, valid_y), step)

    # 早期終了の判定
    if trial.should_prune():
        raise optuna.TrialPruned()

    return clf.score(valid_x, valid_y)

図７アーリーストッピングのコード例

3.5 可視化機能

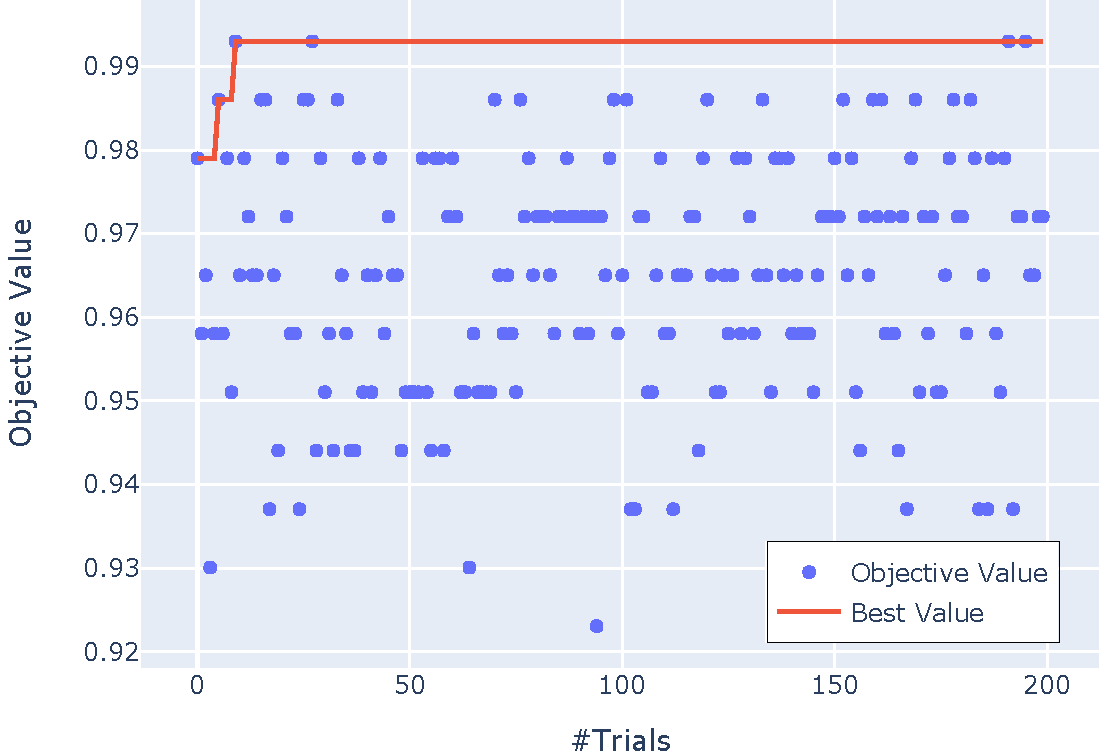
Optunaは，豊富な可視化機能を提供しており，ユーザは最適化の結果の分析と改善をインタラクティブに行うことができる．図８には，可視化の例を二つ示す．

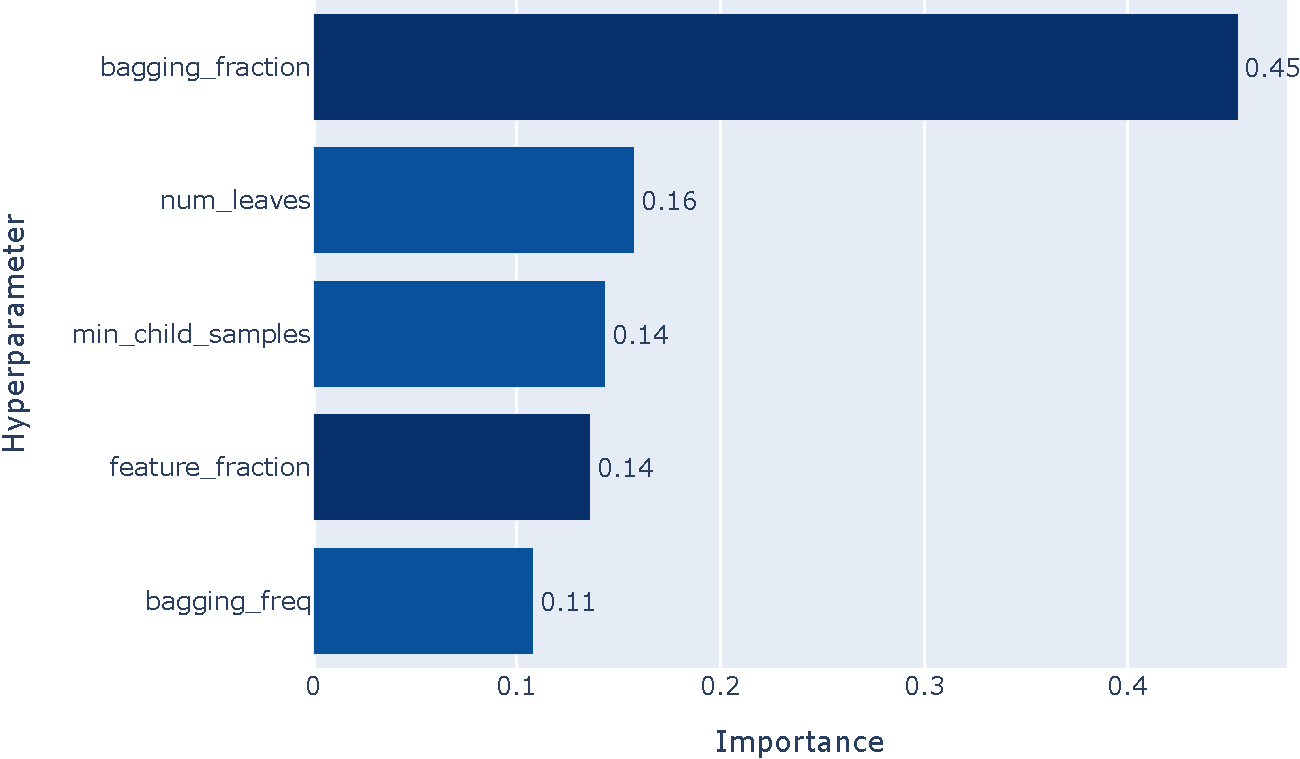
図８(a)は，探索履歴のプロットである．横軸はtrial，縦軸は評価値である．赤線で示された最良値の推移を見ると，探索初期の27 trial目で探索後期と同じ最良値が見つかっていることから，この例では，trial数は十分である様子が伺える．次に，図８(b)に，ハイパパラメータの重要度のプロットを示す．この例では，LightGBM[9]のハイパパラメータのうちbagging_fractionの重要度が大きかったことがわかる．もしtrial数を多くできない場合には，重要度の低いハイパパラメータの値を固定して，探索空間を小さくすることも一つの手段である．

これらの可視化は，最適化済みのstudyを探索履歴プロット関数 plot_optimization_historyや重要度プロット関数 plot_param_importances関数に引数として渡すだけで手軽に試すことができる．

(a) 探索履歴

(b) ハイパパラメータの重要度

図８最適化結果の可視化例

4.1 深層学習ベース音声認識システムの事例

DeepSpeechはMozilla Foundationが開発しているオープンソースの音声認識システムである．DeepSpeechはHannumらの手法[10]を基に，エンドツーエンドの深層学習に基づくアプローチをとっており，スペクトログラムから文字列へと変換する回帰型ニューラルネットワーク(RNN)と，RNNから出力された文字列を補正するN-gram言語モデルから構成される．

式(1)にスコア関数を示す．スコア関数は三つの項から成り\(\log (P(c|x))\)はRNNによる発話\(x\)に対する文字列\(c\)の確率，\(\log (P_{\mathrm{lm}}(c))\)は言語モデルによる文字列\(c\)の確率，\(\mathrm{wc}(c)\)は系列長に対応する．第2項, 第3項の重みである \(\alpha\) と \(\beta\) がハイパパラメータである．適切な\(\alpha, \beta\)の値は，言語やデータセットごとに異なる可能性があり，ハイパパラメータの調整が必要である．

\(Q(c) = \log (P(c|x)) + \alpha \log (P_{\mathrm{lm}}(c)) + \beta \mathrm{wc}(c)\) 式(1)

DeepSpeechの訓練（訂正：モデルの評価）では，~~数千時間に及ぶ~~（訂正：数時間の）音声データと複数のGPUが用いられ，計算機コストが大きくかかる．そこで，DeepSpeechのハイパパラメータ最適化では早期終了を使い，望みのないハイパパラメータの訓練（訂正：評価）を打ち切ることで，最適化時間の短縮が図っている．

4.2 ロボットハンド設計の事例

Koはロボットハンドの設計に，Optunaを応用している[11]．2本の指を持つハンドについて，さまざまな物を持ち上げられる形状を探索している．探索対象の設計パラメータは，リンクの長さや関節中心からベルトまでの距離，ばね定数などである．目的関数は式（２）のようになる．

\(f(\theta) = \prod_{i=1}^{n} \left(1 + \frac{1}{m} \sum_{j=1}^{m} h_j(p_i, \theta) \right) \) 式(2)

ここで\(\theta\) は設計パラメータ，\(h_j(p_i, \theta)\) は作業\(p_i\) において，パラメータ\(\theta\)をもとにして作ったロボットハンドが，対象物を持ち上げた高さを表す．外乱の影響があるため，\(m\)回試行した平均をとっている．これを \(n\)種類の作業についてそれぞれ計算して積をとったものを最終的なスコアとしている．

1回の試行ごとに，ハンドの試作と実験を繰り返すのはコストの観点から現実的ではない．Koは，Optunaがサンプルした設計パラメータをもとにシミュレータ上にハンドを作成し，シミュレータ内での作業の結果をもとに評価値を計算した．

求められた最適なパラメータ下でのシミュレーション結果を図９に示す．小さな物体も大きな物体も適切に把持できている様子が見られる．さらに，このハンドは実機での動作も確認されている．

この例は，ハイパパラメータ最適化の考え方がハードウェアであるロボットの設計にも役立った事例である．シミュレータを活用して計算機と現実世界をつなぐことで，Optunaはハードウェアの設計にも応用可能である．

図9 ロボットハンドのシミュレータ内での動作． (文献[11]より引用)

5．おわりに

本稿では，オープンソースのライブラリであるOptunaを用いたハイパパラメータ最適化の基本的な方法を紹介した．より詳しくは，Optunaのドキュメントを参照されたい．誌面の都合上，コード例はscikit-learnを主に利用したが，PyTorchやLightGBMなどその他の機械学習ライブラリのコード例も豊富に用意している．また，応用事例で述べたように，Optunaの適用範囲は機械学習にとどまらない．読者の研究開発の一助になれば幸いである．

文献

[1] J.N. van Rĳn and F. Hutter, “Hyperparameter Importance Across Datasets,” Proceedings of the 24th ACM SIGKDD International Conference on Knowledge Discovery and Data Mining, p.2367–2376, KDD ’18, 2018.
[2] M. Feurer and F. Hutter, “Hyperparameter Optimization,” Automated Machine Learning, pp.3–33, Springer, Cham, 2019.
[3] 尾崎嘉彦，野村将寛，大西正輝，“機械学習におけるハイパパラメータ最適化手法：概要と特徴，” 信学論 (D)，vol.J103-D，no.9，pp.615–631，2020．
[4] J. Bergstra, R. Bardenet, Y. Bengio, and B. Kégl, “Algorithms for Hyper-parameter Optimization,” NeurIPS, pp.2546–2554, 2011.
[5] J. Snoek, H. Larochelle, and R.P. Adams, “Practical Bayesian Optimization of Machine Learning Algorithms,” NeurIPS, pp.2951–2959, 2012.
[6] F. Hutter, H.H. Hoos, and K. Leyton-Brown, “Sequential Model-Based Optimization for General Algorithm configuration,” LION, pp.507–523, 2011.
[7] K. Jamieson and A. Talwalkar, “Non-stochastic Best Arm Identification and Hyperparameter Optimization,” Artificial Intelligence and Statistics, pp.240–248, 2016.
[8] L. Li, K. Jamieson, G. DeSalvo, A. Rostamizadeh, and A. Talwalkar, “Hyperband: A Novel Bandit-Based Approach to Hyperparameter Optimization,” JMLR, vol.18, no.185, pp.1–52, 2018.
[9] G. Ke, Q. Meng, T. Finley, T. Wang, W. Chen, W. Ma, Q. Ye, and T.-Y. Liu, “Lightgbm: A Highly Efficient Gradient Boosting Decision Tree,” NeurIPS, vol.30, pp.3146–3154, 2017.
[10] A. Hannun, C. Case, J. Casper, B. Catanzaro, G. Diamos, E. Elsen, R. Prenger, S. Satheesh, S. Sengupta, A. Coates, and A.Y. Ng, “Deep Speech: Scaling Up End-to-end Speech Recognition,” 2014.
[11] T. Ko, “A Tendon-Driven Robot Gripper With Passively Switchable Underactuated Surface and its Physics Simulation Based Parameter Optimization,” IEEE Robotics and Automation Lett., vol.5, no.4, pp.5002–5009, 2020.