Blog

7 月から 10 月にかけて Black-Box Optimization Challenge (BBO Challenge) という、機械学習タスクにおけるハイパーパラメータ最適化アルゴリズムの性能を競うコンペティションが開催されました。Preferred Networks とサイバーエージェント AI Lab から Optuna 開発に携わるメンバーが合同で参加し、チーム Optuna Developers として 5 位に入賞しました。本記事では BBO Challenge の概要と我々のソリューションについて紹介します。
BBO Challenge について
BBO Challenge は NeurIPS 2020 の併設コンペティションで、その名が示すようにブラックボックス最適化アルゴリズムの性能を競います。ブラックボックス最適化とは、ある関数の出力を最大化 (または最小化) するような入力を勾配情報などを使わずに探索する問題であり、Optuna が解く問題そのものでもあります。中でも今回の BBO Challenge は、機械学習のハイパーパラメータ最適化をテーマとしており、実際のデータセットに対する機械学習モデルの性能を最適化するものでした。
BBO Challenge のルール
参加者は最適化アルゴリズムを Python のクラスとして実装し、BBO Challenge のシステムに提出します。参加者から提出されたアルゴリズムは bayesmark と呼ばれるベンチマークフレームワークによって評価され、様々な機械学習手法・データセット・評価メトリクスを組み合わせたタスクセットでの平均スコアが算出されます。bayesmark のデフォルトタスクセットでは 9 個の機械学習手法、6 個のデータセット、4 個の評価メトリクスが用意されていますが、BBO Challenge の本番では未知のタスクによって評価され、参加者がこれらのタスクを知ることはできません。
タスク毎には以下のような評価が行われます。評価可能な回数が比較的少なく、バッチ最適化の問題設定であることも特筆すべきポイントです。
- ハイパーパラメータの提案と評価のイテレーションを 16 回繰り返す。
- 各イテレーションにおいて 8 組のハイパーパラメータをまとめて提案する。
- 各ハイパーパラメータに対して交差検証誤差と汎化誤差が算出される。
- 最適化アルゴリズムには交差検証誤差のみが知らされる。
- 全イテレーションの中で最も交差検証誤差に優れたハイパーパラメータを採用し、その汎化誤差が該当タスクにおけるスコアとして記録される。
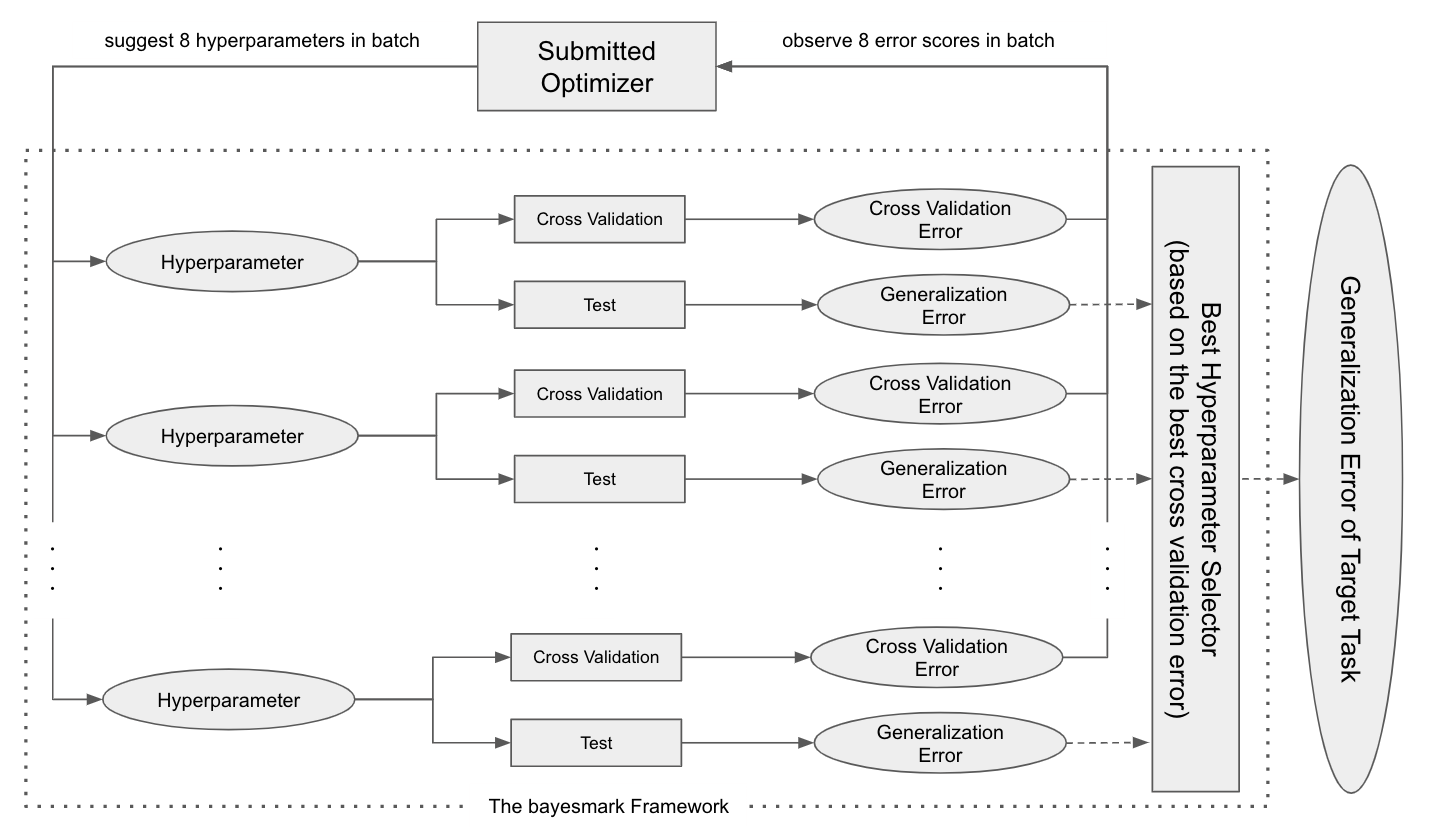
図 1: BBO Challenge におけるタスク毎の評価パイプライン。8 組のハイパーパラメータがバッチで提案・評価される。評価は交差検証と汎化誤差検証に分かれており、交差検証誤差のみが最適化アルゴリズムに知らされる。提案・評価のバッチを 16 回繰り返したのち、交差検証誤差において最も優れたハイパーパラメータが選択され、その汎化誤差がタスクのスコアとして記録される。
また、表 1 に示されるように、実際の機械学習クラスのハイパーパラメータを調整するため、浮動小数点・整数・カテゴリカルといった様々なデータ型が混在するほか、log や logit のような値のスケールが指定されることもあります。
表 1: bayesmark における Lasso 回帰モデルの探索空間
| ハイパーパラメータ名 | 値の型 | 値のスケール | 値のレンジ |
| alpha | float | log | [1e-2, 1e2) |
| fit_intercept | bool | N/A | {True, False} |
| normalize | bool | N/A | {True, False} |
| max_iter | int | log | [10, 5000) |
| tol | float | log | [1e-5, 1e-1) |
| positive | bool | N/A | {True, False} |
我々のソリューションについて
今回のコンペティションにおいて、我々が着目したのは以下のような点です。
- バッチ最適化問題である
- 目的関数の滑らかさに関する性質が未知である
- 量的変数と質的変数が混在した探索空間である
- 評価可能な回数が比較的少ない
ベースライン手法として、バッチ最適化で優れた性能を示す TuRBO [1] を採用し、そこにいくつかの工夫を加えました。目的関数の滑らかさに向けては『マルチカーネル』と『停滞回避のためのリスタート』、量的変数と質的変数が混在した探索空間に向けては『限定的なトラストリージョンの絞り込み』と『網羅的探索』、評価回数の少なさに向けては『Sobol 列による初期化』という工夫を加えています。
以下では、ベースライン手法とそれぞれの工夫について説明します。
ベースライン手法: TuRBO
我々は TuRBO と呼ばれる手法をベースにしました。TuRBO はガウス過程とトンプソンサンプリングを利用するベイズ最適化アルゴリズムで、特に今回のようなバッチ最適化の問題において高い性能を示します。また、TuRBO はトラストリージョンと呼ばれる矩形を保持しており、その矩形の内部に限定して次のハイパーパラメータをサンプリングします。スコアが改善しない場合には最良解を中心とした上で矩形を小さくし、狭い領域に集中した最適化を試みます。逆に、スコアが改善している場合には矩形を大きくし、より大域的な最適化を試みます。
TuRBO におけるハイパーパラメータの選択は以下の式で示されます。
\[\hat{\bf x} \in \mathrm{argmin}_{{\bf x} \in {\rm TR}} f^{(i)}_{\bf x}\]
\(f^{(i)}_{\bf x}\) はトラストリージョン内の点におけるガウス過程の事後分布からの \(i\) 番目のサンプル \(f^{(i)}_{\bf x} \sim \mathcal{GP}(\mu({\bf x}), k({\bf x}, {\bf x}^{\prime}))\) を示します。
TuRBO には単一のトラストリージョンのみを保持する TuRBO-1 と複数のトラストリージョンを同時に使う TuRBO-m があります。我々がベンチマークをとった限りでは TuRBO-1 の方が優れた性能を示していたため、今回は TuRBO-1 のみを利用しました。以下では簡単のため、TuRBO-1 を TuRBO と表記します。
マルチカーネル
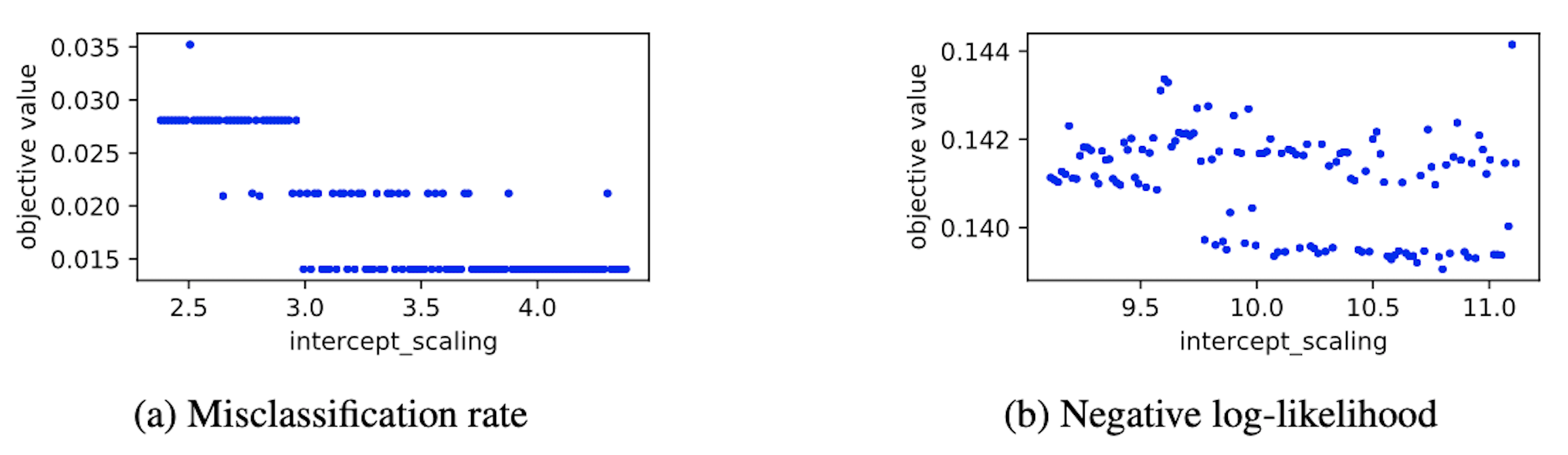
ガウス過程による代理モデルの近似性能はカーネル関数によって大きく左右されます。通常、カーネル関数は問題の性質を鑑みて設定され、特に目的関数の滑らかさを反映したものを選択します。しかし、今回のケースでは問題の性質を事前に知ることができず、図 2 (左) に示されるような平らな関数や図 2 (右) に示されるような凹凸のある関数が問題毎にやってきます。
図 2: ある試行における最良ハイパーパラメータ周辺での目的関数の形状の例。左と右の図はいずれも Lasso クラス分類器の最適化結果で、それぞれ誤分類率と負の対数尤度についてのプロットを示す。
この課題への対処として、複数のカーネルをアンサンブルする手法を取り入れました。具体的にはハイパーパラメータの選択方法を以下の式のように変更し、複数の代理モデルから候補をサンプリングし、それらの候補の和集合から次のハイパーパラメータを選びました。
\[\hat{\bf x} \in \mathrm{argmin}_{\bf{x} \in {\rm TR}}
\left\{
f^{(i)}_{{\bf x}, k}
\mid
k \in \mathcal{K}
\right\}
\]
\(f^{(i)}_{{\bf x}, k}\) はカーネル関数 \(k\) によるガウス過程の事後分布からの \(i\) 番目のサンプル \(f^{(i)}_{{\bf x}, k} \sim \mathcal{GP}(\mu({\bf x}), k({\bf x}, {\bf x}^{\prime}))\) であり、\(\mathcal{K}\) は事前に定義されるカーネル関数の集合です。
停滞回避のためのリスタート
TuRBO が同じ評価値を出し続け、一向にスコアが改善されない問題に悩まされました。図 2 (左) のように目的関数が平らで階段状になっている場合には、トラストリージョンがある段に停滞し続け、最適化が実質そこで止まってしまいます。この問題への対処として、同じ評価値が一定回数続いた場合にはトラストリージョンの更新をリスタートする仕組みを取り入れました。
限定的なトラストリージョンの絞り込み
TuRBO は連続値の入力を想定しているため、カテゴリカル・ブーリアン型はワンホット表現などを通して扱われます。一方で、トラストリージョンを絞る際には矩形サイズが減衰していくため、ワンホット表現の片方の端点はすぐに矩形から外れてしまい、探索が片方の値に偏る傾向にありました。これに対処するため、一定の評価回数に到達するまでは、カテゴリカル・ブーリアン型に限ってはトラストリージョンを絞らないようにしました。
また、値のスケールが logit に指定されている場合にも同様の処理を施しました。図 3 (c) に示されるように、logit 関数によって候補点が両端点付近に偏り、ワンホット表現と同様の問題が起きるためです。
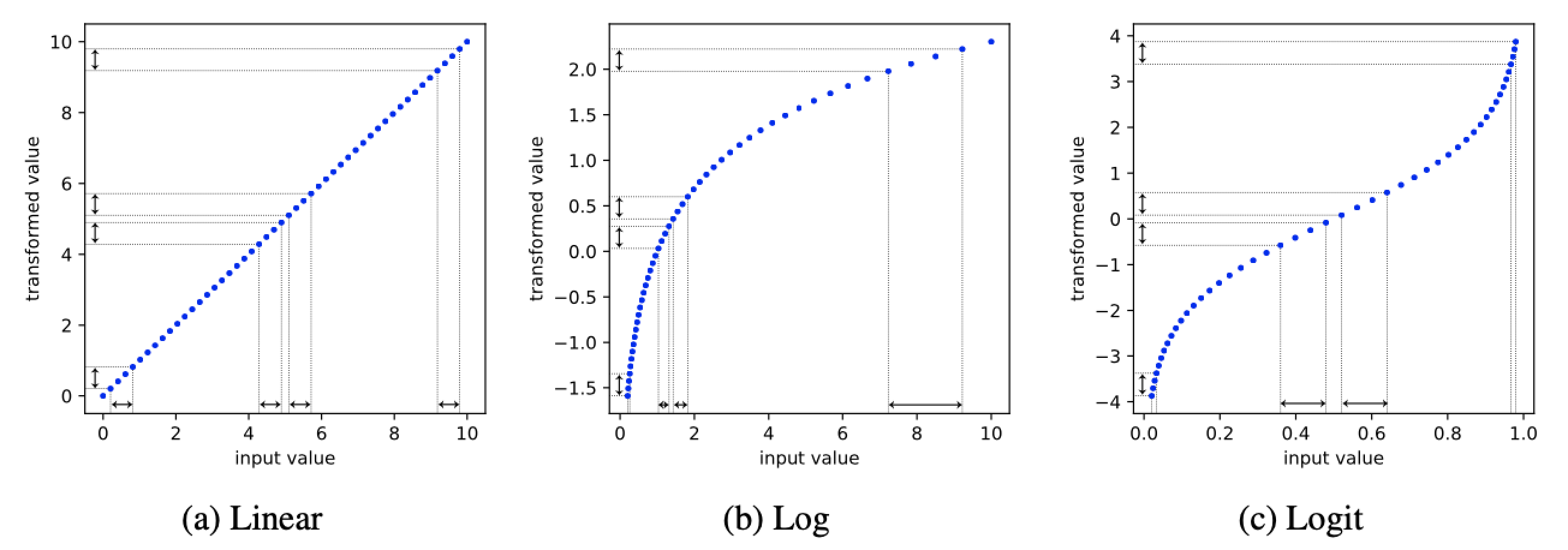
図 3: 値のスケールの可視化。縦軸は元の探索空間における値で横軸はスケーリング後の値を示す。log 関数 (b) では探索範囲の左側、logit 関数 (c) では探索範囲の両端にスケーリング後の値が偏る。
網羅的探索
探索空間が離散的で十分に小さい場合、特に全てのハイパーパラメータ候補の数が高々評価可能な回数以下の場合には網羅的探索によって全ての解を評価できます。一方、そのような探索空間において、TuRBO をはじめとするハイパーパラメータ最適化アルゴリズムは陽に避けない限り同じ候補を探索してしまうことがあります。そこで、探索空間が上記の条件を満たす場合には、網羅的探索に切り替えるロジックを加えました。
Sobol 列による初期化
TuRBO の初期化にはラテン超方格法と呼ばれるアルゴリズムが使われています。これは探索空間をできるだけ網羅するような代表点を選択するアルゴリズムですが、一般に点の数が少ない場合には Sobol 列 [2] が一様性においてより優れた代表点を生成できることが知られています。今回のタスクは評価可能な回数が比較的少ないため、Sobol 列による初期化を採用しました。
Bayesmark による評価実験
提案手法をベースライン手法の TuRBO と比較し、更に提案手法から工夫を 1 つずつ落としたアブレーション評価を行いました。
評価実験には bayesmark のデフォルトタスクセットを使いました。各タスクの繰り返しを 10 回に設定し、bayesmark-agg コマンドによって交差検証誤差* を集計しました。更に実験毎の分散を抑えるため、この操作を 30 回繰り返した平均スコアを比較しています。
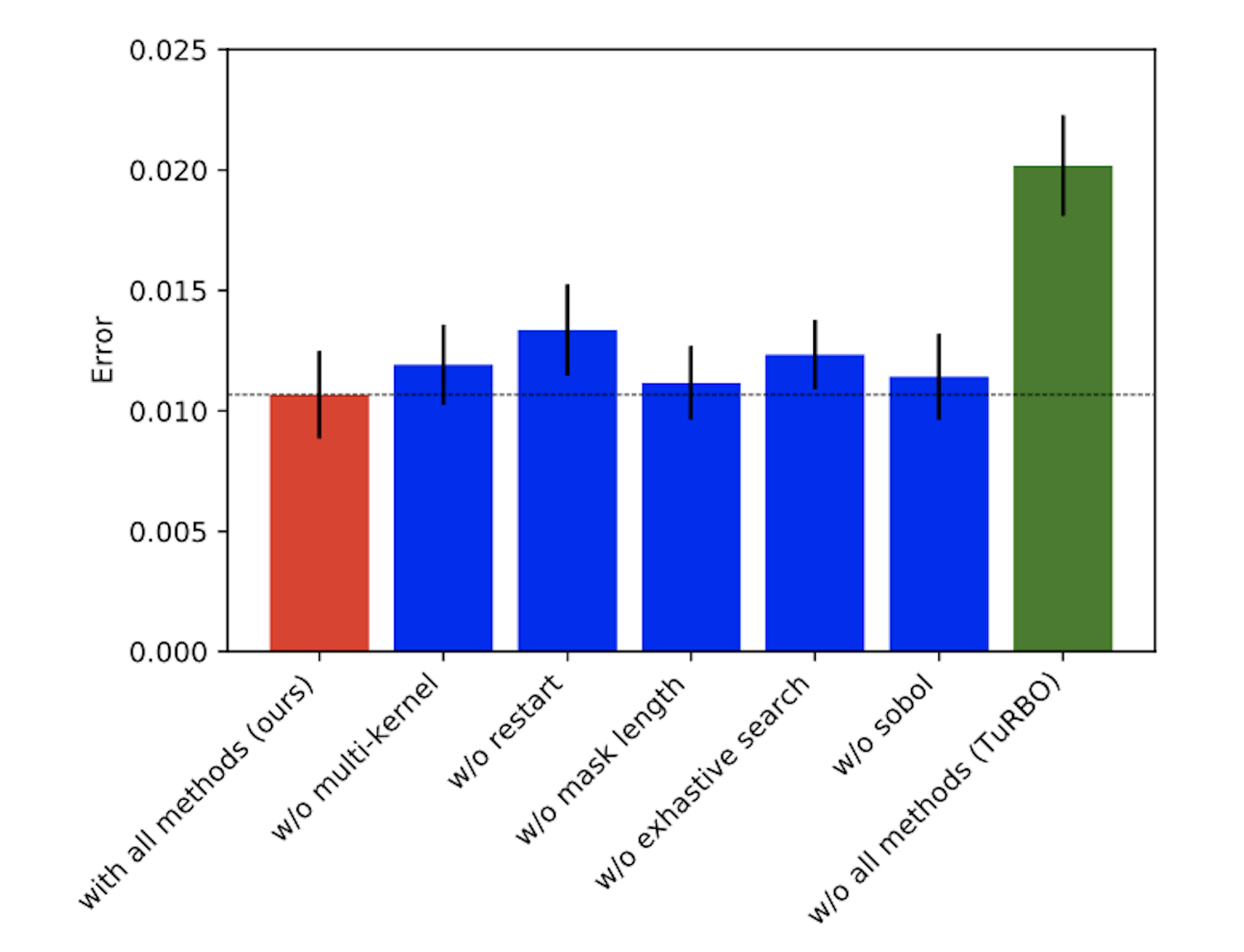
図 4 はエラーの評価結果で、一番左が提案手法、一番右が TuRBO の結果となります。提案手法において、エラーが大きく改善していることが確認できます。
図 4: bayesmark による比較実験の結果。縦軸は交差検証での平均誤差であり、一番左と一番右の棒はそれぞれ提案手法と TuRBO の性能を示す。中央の 5 つの棒は前章で説明されるそれぞれの工夫についてのアブレーション評価結果を示す。
中央の 5 つの棒はそれぞれの工夫についてのアブレーション評価の結果です。いずれの工夫もそれを抜くことでエラーが改悪しており、それぞれが提案手法のパフォーマンスに貢献していることが確認できます。中でも『マルチカーネル』と『停滞回避のためのリスタート』によるパフォーマンスの差は大きく、様々な目的関数の性質に対処することが重要なポイントであったと言えます。また『網羅的探索』の貢献も大きく、一部のタスクにおいては確実に探索点の重複を避けることも重要であると言えます。
* 後述のように bayesmark のデフォルトタスクでは交差検証誤差と汎化誤差の乖離が激しく、問題の切り分けのため交差検証誤差を利用している。
BBO Challenge の結果
BBO Challenge の評価には、上記の実験に使ったタスクセットとは別のものが用意されており、このタスクセットは参加者には伏せられています。また Kaggle をはじめとするコンペティションプラットフォームと同様に、期間中のリーダーボード (public leaderboard) とは別のタスクセットによって最終成績 (private leaderboard) が決まります。
提案手法の public leaderboard でのスコアは 96.939 で、終了時点では 9 位の成績でした。また、ベースライン手法の TuRBO を提出した際のスコアは 95.491 で、リーダーボード上でもスコア改善されていることが確認できました。
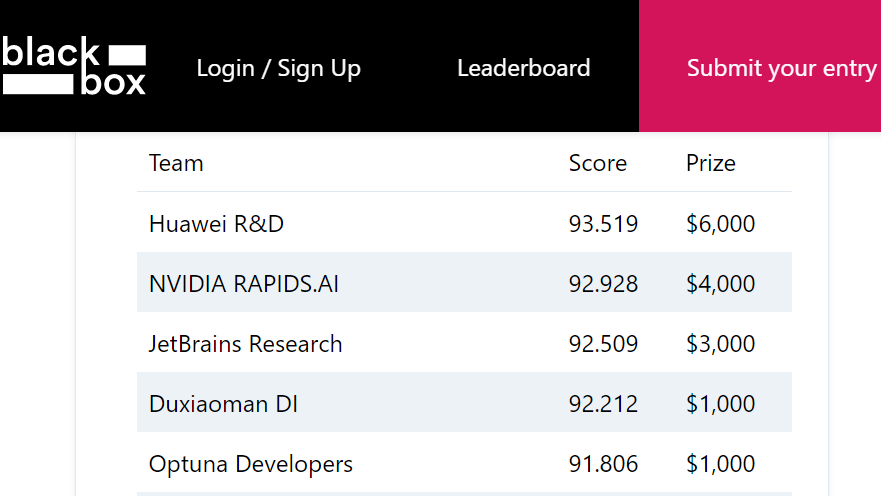
コンペ終了後に公開された private leaderboard でのスコアは 91.806 で 5 位となり、public leaderboard から大きく順位を伸ばしての入賞となりました。
図 5: BBO Challenge の最終結果
課題:汎化誤差の扱いについて
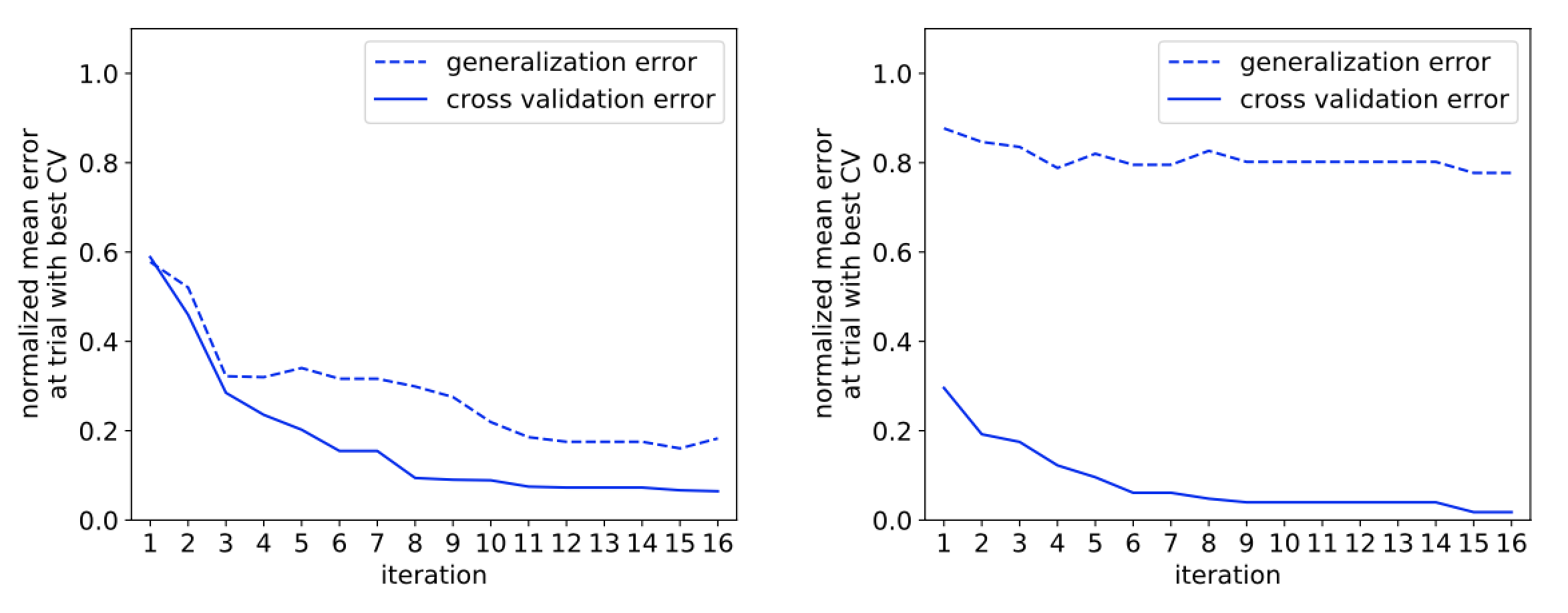
解決できなかった課題の一つとして、交差検証誤差と汎化誤差の乖離が挙げられます。これは現実のハイパーパラメータ探索においても散見される問題ですが、一部のタスクにおいて、交差検証誤差が改善されても汎化誤差が全く改善されない、もしくは改悪されてしまう現象 (図 6) が起きていました。更に、交差検証誤差が低いハイパーパラメータ群ほど汎化誤差との乖離が大きい傾向にあり (図 7)、最適化アルゴリズムの微妙な改善を評価することが難しくなっていました。
一因として bayesmark に使われるデータセットの性質が挙げられます。デフォルトのデータセットには scikit-learn のトイタスクが使われており、サイズが比較的小さなものに偏っています。したがって、スプリットの際にデータの性質が均等にならないことも多く、このような乖離が生まれやすいと考えられます。
本番のタスクセットはその趣旨も含めて内容が伏せられており、タスクの性質に仮定を置くことが難しいのも悩みの一つでした。デフォルトタスクでの汎化性能を向上させたからといって、必ずしも本番の汎化性能向上につながるとは限りません。
問題の切り分けのため、我々のチームでは交差検証のみに注目し、この種のノイズが無いと仮定した上での最適化性能を評価していました。一方で、この点を意識して評価方法を工夫したチームもあり、例えば 2 位に入賞した NVIDIA RAPIDS.AI チームは bayesmark に手を入れていくつかの追加データセット・機械学習手法でも評価していたようです。
図 6: digits データセットにおいて AdaBoost (左) と kNN (右) を最適化した際のスコア推移の一例。左側の図では交差検証誤差と汎化誤差の改善が一貫している一方で、右側の図では汎化誤差の改善がほとんどみられない。
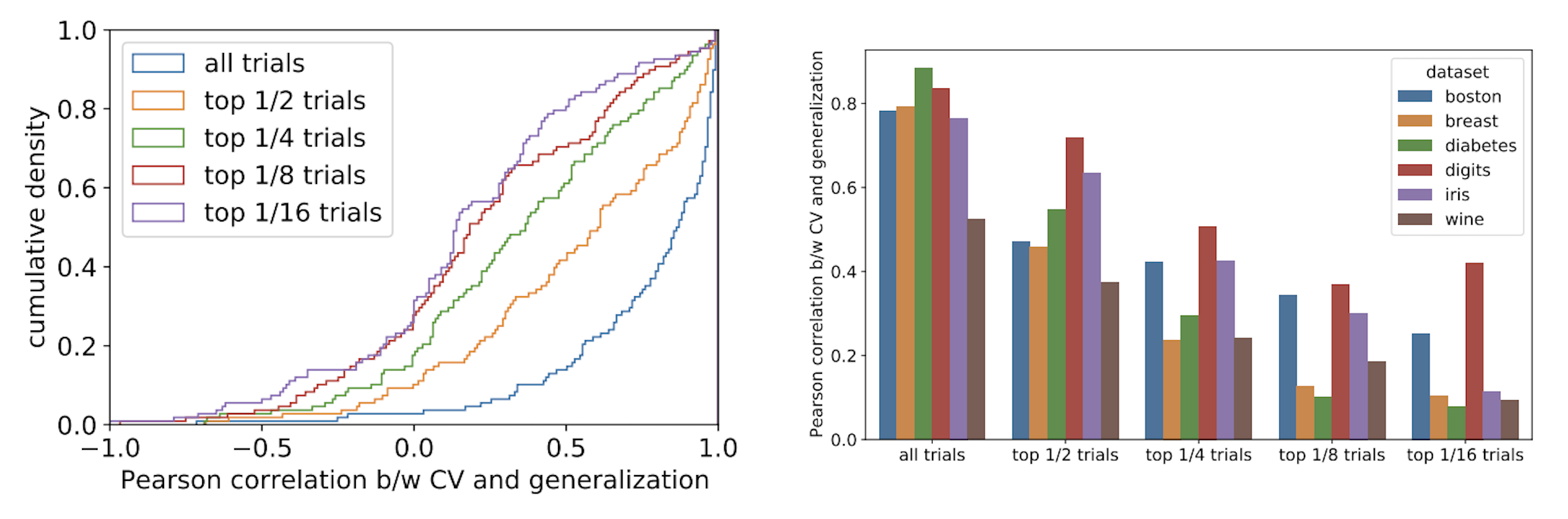
図 7: bayesmark のデフォルトタスクにおける交差検証誤差と汎化誤差の相関についての集計。左: ピアソン相関係数の累積分布関数であり、それぞれの線は交差検証誤差について上位 1/16, 1/8, 1/4, 1/2, 及び全てのハイパーパラメータ群に対応する。全てのハイパーパラメータ群では交差検証誤差と汎化誤差の相関が比較的高いものの, 集計を上位の群に絞るにつれて相関が低くなる傾向にある。右: ハイパーパラメータ群とデータセット毎のピアソン相関係数の平均。相関係数の減少傾向はデータセットによって異なる。
BBO Challenge を通して
今回は Optuna 開発に携わるメンバー数名のチームとして参加しておりました。開発チームとしての知見を広げることが主な目的でしたが、TuRBO をはじめとするアルゴリズムの実践上の課題を洗い出す良い機会となりました。
bayesmark は従来のベンチマークフレームワーク* に比べて多種多様な機械学習タスクとメトリクスが用意されているため、現実のハイパーパラメータ最適化にも散見される問題が浮き彫りとなりました。例えば、変則的な目的関数の形状に着目したり、場合によっては網羅的探索のようなナイーブな方法に切り替えるなど、多くの最適化アルゴリズムが見落としがちなシナリオへの対応も必要でした。
また、BBO Challenge は Optuna の可視化機能を実践する機会でもありました。本記事で紹介した工夫に辿り着くまでには bayesmark のタスクの性質を知る必要がありましたが、スライスプロットを使った目的関数の形状可視化や、重要度プロットによる支配的なハイパーパラメータの傾向分析が役に立ちました。開発チームでは、Optuna が自動最適化アルゴリズムを提供するだけではなく、問題の性質を理解する手助けとなることも重要であると考えています。
* sigopt evalset, COCO, HPOBench など
おわりに
BBO Challenge で得た成果・知見は随時 Optuna へと反映される予定です。本記事で紹介したアプローチ以外にも CMA-ES に基づく手法も試しており、一部は既に Optuna の機能としてリリースされています。
最後に、共に Optuna Developers として出場したサイバーエージェント AI Lab の芝田様と野村様、および本プロジェクトにご協力くださった皆様に深く感謝いたします。
参考文献
- David Eriksson, Michael Pearce, Jacob Gardner, Ryan D Turner, and Matthias Poloczek. Scalable global optimization via local bayesian optimization. In Advances in Neural Information Processing Systems, pages 5496–5507, 2019.
- Sergei Kucherenko, Daniel Albrecht, and Andrea Saltelli. Exploring multi-dimensional spaces: A comparison of latin hypercube and quasi monte carlo sampling techniques. arXiv preprint arXiv:1505.02350, 2015.