Blog
本記事は 2020 年夏季インターンシップに参加された今木翔太さんによる寄稿です。
東京大学の今木翔太です。大学院では理論物理を研究しています。
インターンでは、機械学習を用いた数量ファイナンスをテーマに、個人的に関心のあった Deep Hedging の研究を行いました。
デリバティブと呼ばれる金融商品を深層学習を用いてヘッジする Deep Hedging は、ニューラルネットワークの学習が難しいことが課題でした。私たちは、No-Transaction Band ネットワークというネットワーク構造を提案し、学習を 20 倍以上効率化しました。複雑な金融商品も数秒オーダーで学習し、価格付けできるようになります。
この成果により、人工知能学会の研究会優秀賞を頂くことができました。大変光栄に感じています。また、Google Colab 上で動くミニマルな実装と、Deep Hedging の汎用ライブラリ PFHedge を GitHub に公開しました。
- 人工知能学会論文:効率的なDeep Hedgingのためのニューラルネットワーク構造
- より詳しい論文:No-Transaction Band Network: A Neural Network Architecture for Efficient Deep Hedging
- 論文の実装:pfnet-research/NoTransactionBandNetwork
- Deep Hedging ライブラリ:pfnet-research/pfhedge
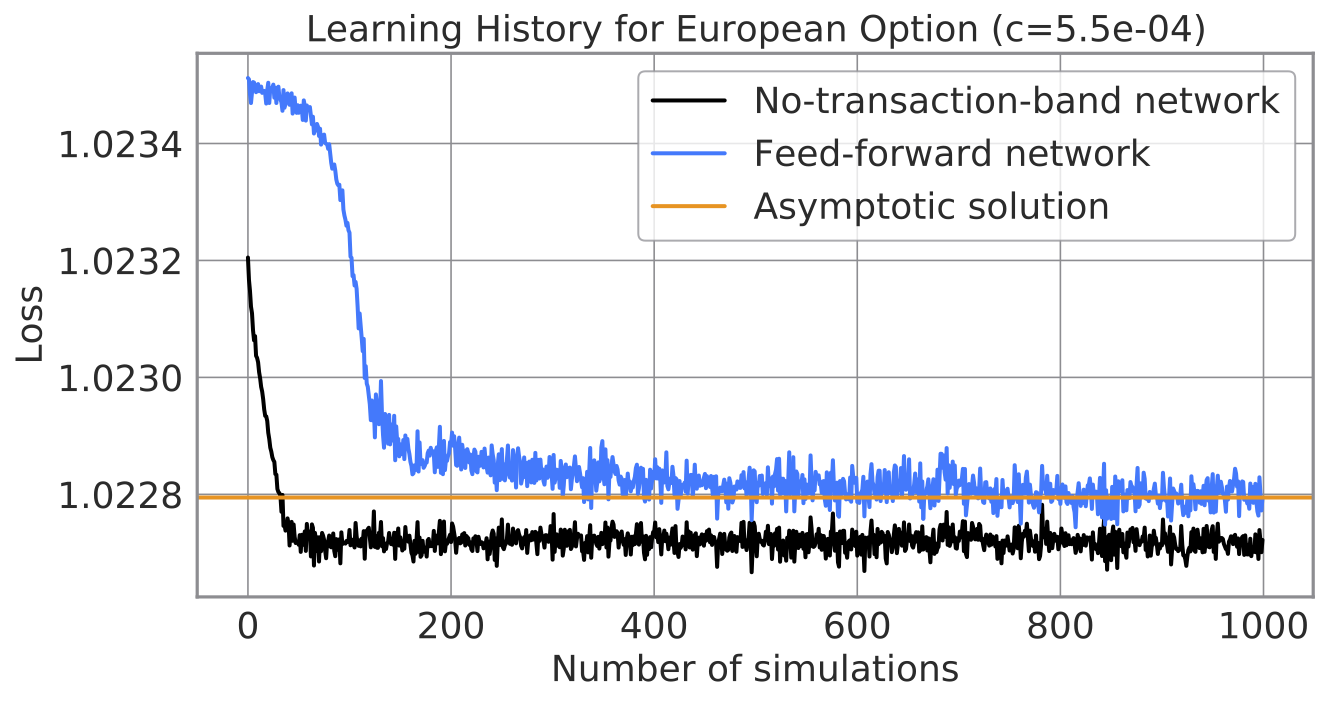
(図) 従来のニューラルネット構造の学習曲線(青)と、私たちが提案するニューラルネット構造の学習曲線(黒)。
研究の目標:ヘッジ取引の自動化
研究の目標は「証券会社のデリバティブ販売に伴うヘッジ取引を自動化すること」です。デリバティブ・ヘッジ取引について説明し、深層学習でヘッジを自動化する Deep Hedging を紹介します。
デリバティブ
デリバティブは、株・債券・通貨といった通常の金融商品から派生してつくる証券です。たとえば、株のデリバティブは、株価の変動のしかたに連動してその価値が決まります。具体例は次のような証券です。
- ヨーロピアン・コールオプション:定められた期間の最終株価 \(S\) と基準価格 \(K\) に対して、\(\max(S – K, 0)\) の金額を払い出す証券です。
- ルックバック・コールオプション:定められた期間までの株価の最大値 \(M\) と基準価格 \(K\) に対して、\(\max(M – K, 0)\) の金額を払い出す証券です。
デリバティブをうまく使うと、資産や収支に保険をかけたり、柔軟にリスクをとった投機ができます。デリバティブは企業のリスク管理や先進的な投資に必須であり、グローバルに莫大な市場をもつ重要な証券です。
ヘッジ取引
証券会社は、企業や投資家にデリバティブを販売しています。販売に伴い売りポジションを抱えるため、しばしばこのリスクを通常の金融商品でヘッジします。たとえば、株のデリバティブの価値は株価に対してなんらかの”感応度”で変動すると期待できるため、適切な量の株を売買してリスクを相殺できます。
取引コストがないなどの理想的な仮定のもとでは、最適なヘッジ戦略が精密に求められます。つまり、伝統的な定量ファイナンスのモデルに則ってデリバティブの”感応度”を計算し、感応度を相殺するよう時々刻々と取引して無リスクを実現するのが最適な戦略です。
一方、現実の市場には取引コストがあり、最適なヘッジ戦略を必ずしも系統的に求められないため、ヘッジ取引の実務に人手を要します。つまり、証券会社の人間のトレーダーが、定量モデルの出力を参考にしつつ、これを経験に基づいて調整することでヘッジ取引をしています。
しかし、人手でのヘッジは、多大な人的コストがかかる・捌ける注文量が限られるなどの問題があります。そのため、証券会社にとってヘッジ取引の自動化は重要な課題です。

(図) 人間の脳で表現されたヘッジ取引戦略の模式図
先行研究:Deep Hedging
Deep Hedging (Buehler et al. 2018) は、深層学習でヘッジ取引を自動化するフレームワークです。ヘッジ取引戦略をニューラルネットで表現し、学習によって最適ヘッジ戦略を追求します。Deep Hedging の活用により、最大 80% のコスト削減が見込まれ、デリバティブ産業における Game Changer と期待されています。
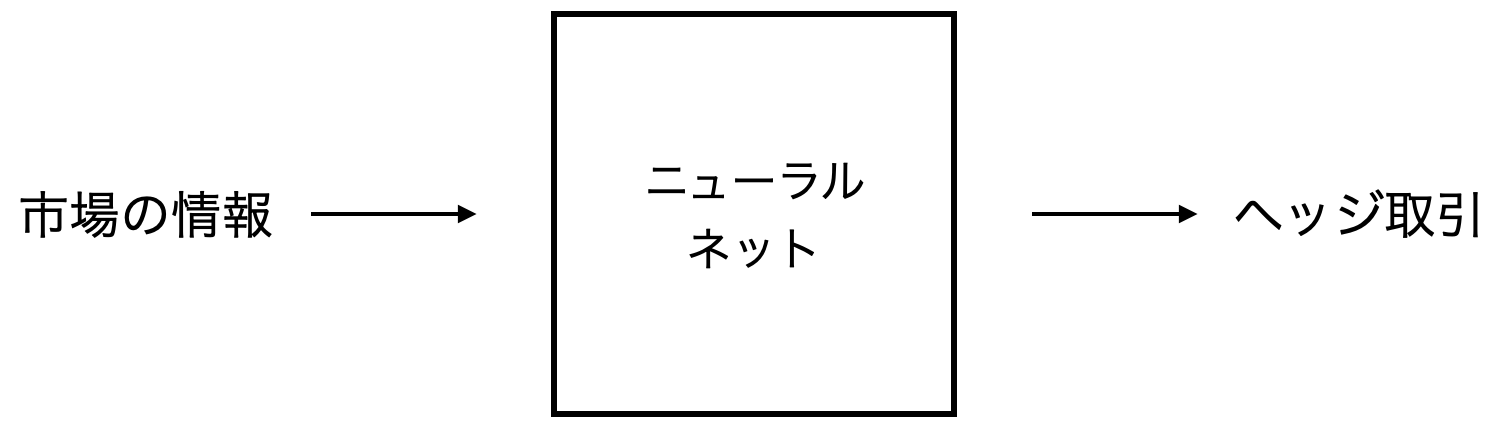
(図) ニューラルネットで表現されたヘッジ取引戦略の模式図
ところが、Deep Hedging には、ニューラルネットの学習が難しいという問題があります。つまり、大量の学習を経ても最適ヘッジ戦略に収束しないことがあります。顧客の注文を素早く正確に請けることを競争力とする証券会社にとって、致命的な問題です。
そこで、私たちは、Deep Hedging の学習を圧倒的に効率化するニューラルネット構造を提案しました。下図のように、元論文で提案されたニューラルネットに比べ、20 倍以上の高速化に成功しています。
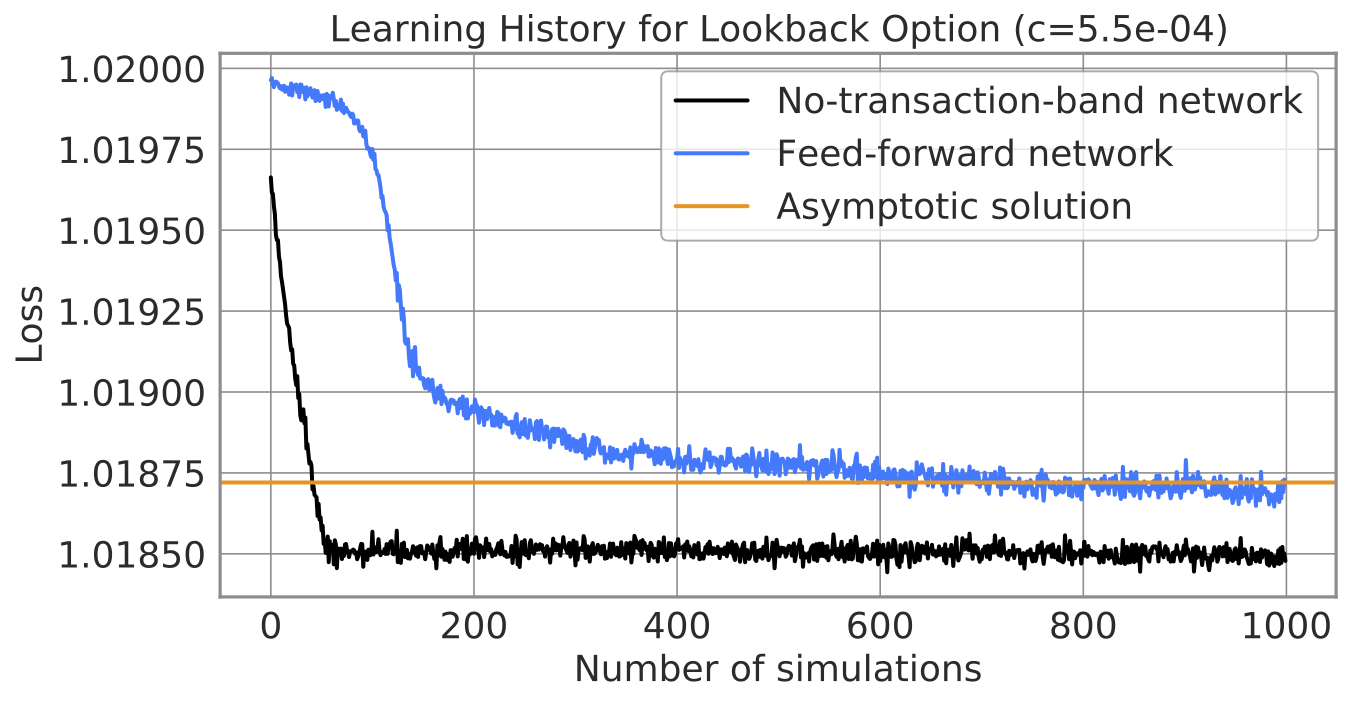
(図) 元論文のニューラルネット構造の学習曲線(青)と、私たちが提案するニューラルネット構造の学習曲線(黒)。
ヘッジ最適化
Deep Hedging および私たちの提案手法を紹介するために、ヘッジ最適化問題を定式化します。なお、ここでの定式化は Deep Hedging の元論文から大幅に単純化しています。
証券会社は、デリバティブを顧客に売り、通常の資産を売買してヘッジします。このことを整理すると、時刻 \(t = 0,, \dots, T\) でヘッジ取引を行ったあとの最終損益を次のように表せます。各項はそれぞれ、デリバティブの売りによる損益・通常の資産の値動きによる損益・取引コストの支払いです。
\( P = -Z + \sum_{t = 0}^{T – 1} (\delta_t \Delta S_t – c |\Delta \delta_t| S_t) \)
ここで \(Z\) はデリバティブの最終価値(株価の経路の関数)、\(\delta\) は各時刻の保有株数、\(S\) は株価、\(c\) は取引コスト率です。株価は確率的に変動すると考えるため、損益 \(P\) も確率変数です。
リスク指標は、証券会社の効用 \(u\) に対して次の損失関数です。この損失関数を最小化する戦略 \(\delta\) を最適ヘッジ戦略と定義します。
\( \ell(\delta) = -\mathbf{E} [u(P)] \)
つまり、最適ヘッジ戦略は「ヘッジ取引後の損益の期待効用を最大化する戦略」といえます。効用は通常は上に凸な増加関数なので、損益 \(P\) の平均を大きく・分散を小さくすることが目標であり、直観的にはリスク削減とコスト節約のトレードオフです。つまり、こまめに保有株数を調整するとリスクが削減できる一方で取引コストがかさむため、ちょうどよい間隔で保有株数を調整することが必要です。
Deep Hedging
Deep Hedging のキーアイデアは、ヘッジ戦略 \(\delta\) をニューラルネットで表現することです。元論文では、次の図のように、現時刻の市場の情報と現時刻の保有株数をインプットし、次時刻の保有株数をアウトプットします。
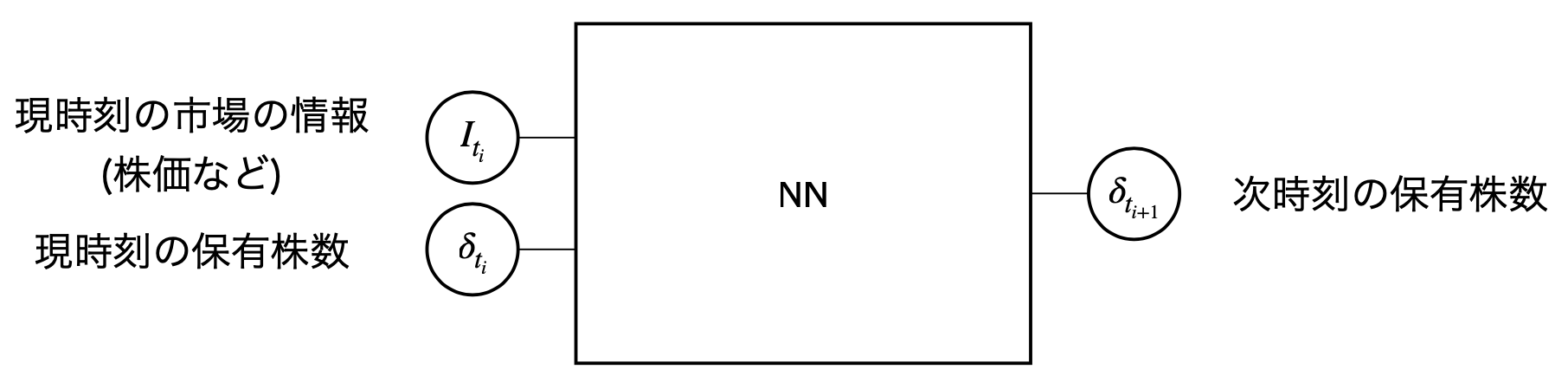
(図)元論文のニューラルネット構造の模式図。
多数の株価パスを確率的にシミュレートし、ニューラルネットにヘッジさせると、その損益分布から損失関数を計算できます。損失関数から逆伝播してニューラルネットのパラメータを更新することを繰り返せば、最適ヘッジ戦略をニューラルネットワークで近似できると期待できます。
ところが、Deep Hedging は学習が難しいという問題があります。前掲の学習曲線のように、1000 回以上のシミュレーションを繰り返しても収束しないことがあります。私たちは、難しさの原因は「ニューラルネットのインプットが現時刻の保有株数に依存すること」と考えました。つまり学習のためにニューラルネットが様々なアウトプットを出力するケースを観測する必要があるため、学習に時間がかかります。
提案:No-Transaction Band ネットワーク
そこで、私たちは No-Transaction Band ネットワークという構造を提案しました。No-Transaction Band ネットワークの構造はシンプルです。次の二手順で、次時刻の保有株数をアウトプットします。
- ニューラルネットが現在の市場の情報をインプットし、次時刻の保有株数の許容幅 \([b_{\text{l}}, b_{\text{u}}]\) を出力する。
- 現時刻の保有株数が許容幅の外にあるときだけ、最小限の取引をして許容幅に収める。
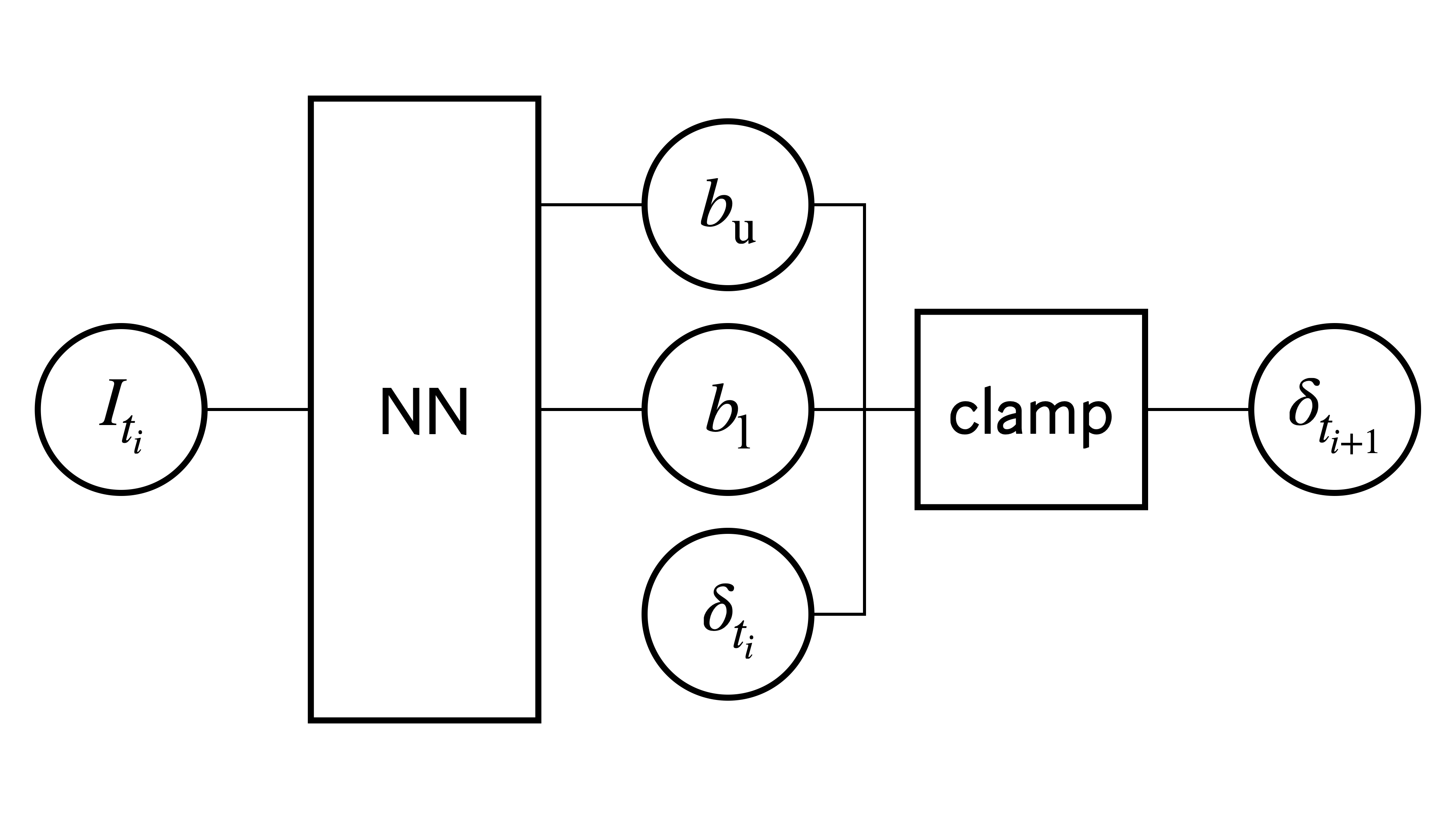
(図)No-Transaction Band Network の模式図。
ここで図の \(\mathsf{clamp}\) は次の式で与えられます。PyTorch の \(\mathsf{clamp}\) 関数で実装できます。
$$ \mathsf{clamp}(\delta_{t_i}, b_{\text{l}}, b_{\text{u}}) = \begin{cases} b_{\text{l}} & \text{if } \delta_{t_i} < b_{\text{l}} \\ \delta_{t_i} & \text{if } b_{\text{l}} \leq \delta_{t_i} \leq b_{\text{u}} \\ b_{\text{u}} & \text{if } \delta_{t_i} > b_{\text{u}} \end{cases} $$
No-Transaction Band ネットワークには、二つの特長があります。
- ニューラルネットのインプットが過去の行動に依存しない:ニューラルネットは現時刻の保有株数をインプットしません。これにより上述の難しさを回避し、学習を加速します。
- 効率的な戦略をヒントとして教えることができる:許容幅を用いた戦略は、保有株数が許容幅を出ない限り取引をしないため、効率的にコストを節約できることが期待できます。この “帰納バイアス” をニューラルネットにヒントとして教え、効率化を促します。
二点目について補足します。この戦略は No-Transaction Band 戦略と呼ばれ、指数効用のもとでヨーロピアン・オプションの最適ヘッジ戦略を与えることが知られていました。私たちは、より一般の効用・デリバティブに対しても、この戦略が最適であることを証明しました。このことと普遍近似定理を考え合わせれば、No-Transaction Band ネットワークが最適ヘッジを表現できることを理論的に保証できます。この保証は、最適ヘッジ戦略を通して顧客に最善のプライスを提供することを付加価値とする証券会社にとって、必須の条件です。
数値実験
No-Transaction Band ネットワークの優位性を実証するため、数値実験を行いました。上述のヨーロピアン・オプションおよびルックバックオプションを、三つの方法でヘッジし比較します。
- No-Transaction Band ネットワークを用いた Deep Hedging:提案手法です。
- 通常の順伝播型ネットワークを用いた Deep Hedging:元論文が提案するネットワークです。
- 低コスト極限における最適ヘッジ戦略の解析解:先行文献で解析的に求められた、取引コスト率が無限小の極限における最適ヘッジ戦略です。
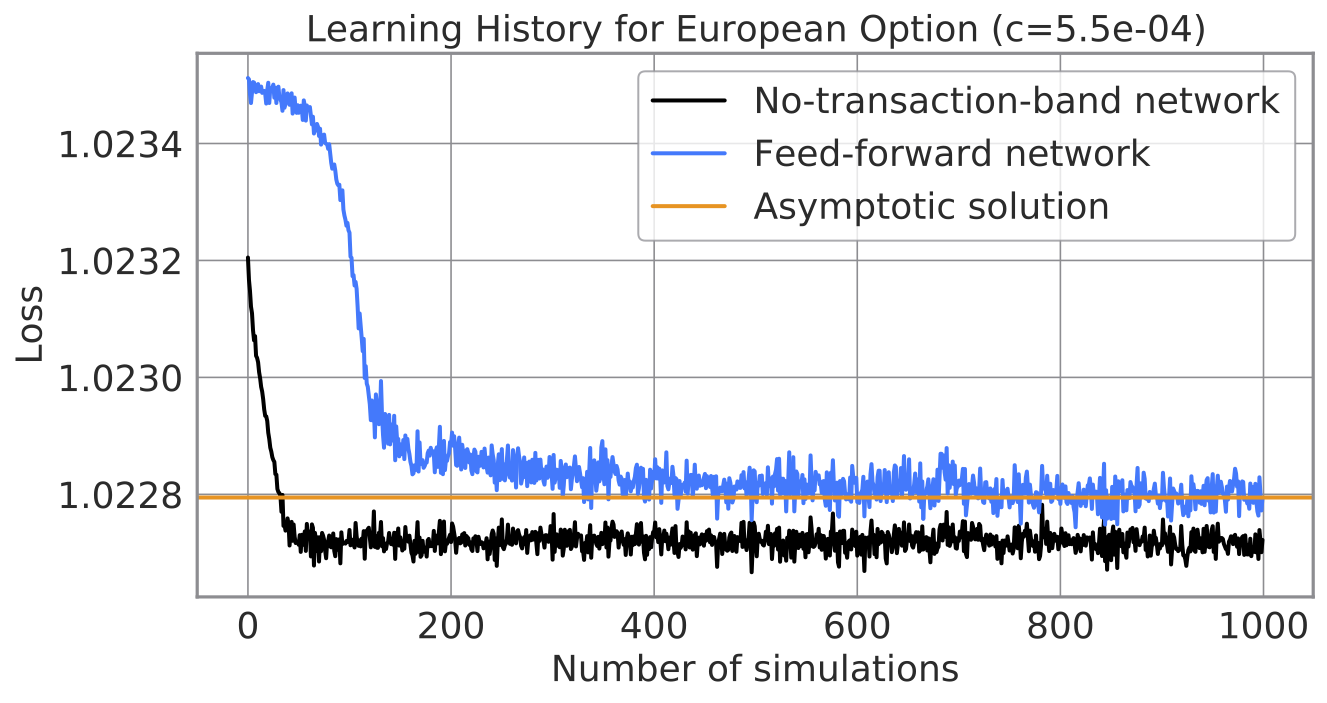
下図に示すように、No-Transaction Band ネットワークの学習は高速です。通常の順伝播型ニューラルネットが 1000 回のシミュレーションを経ても収束しない一方、No-Transaction Band ネットワークは 50 回程度のシミュレーションで収束します。学習時間は PFN の MN-2 で数秒オーダーであり、実用にたえる水準と期待しています。
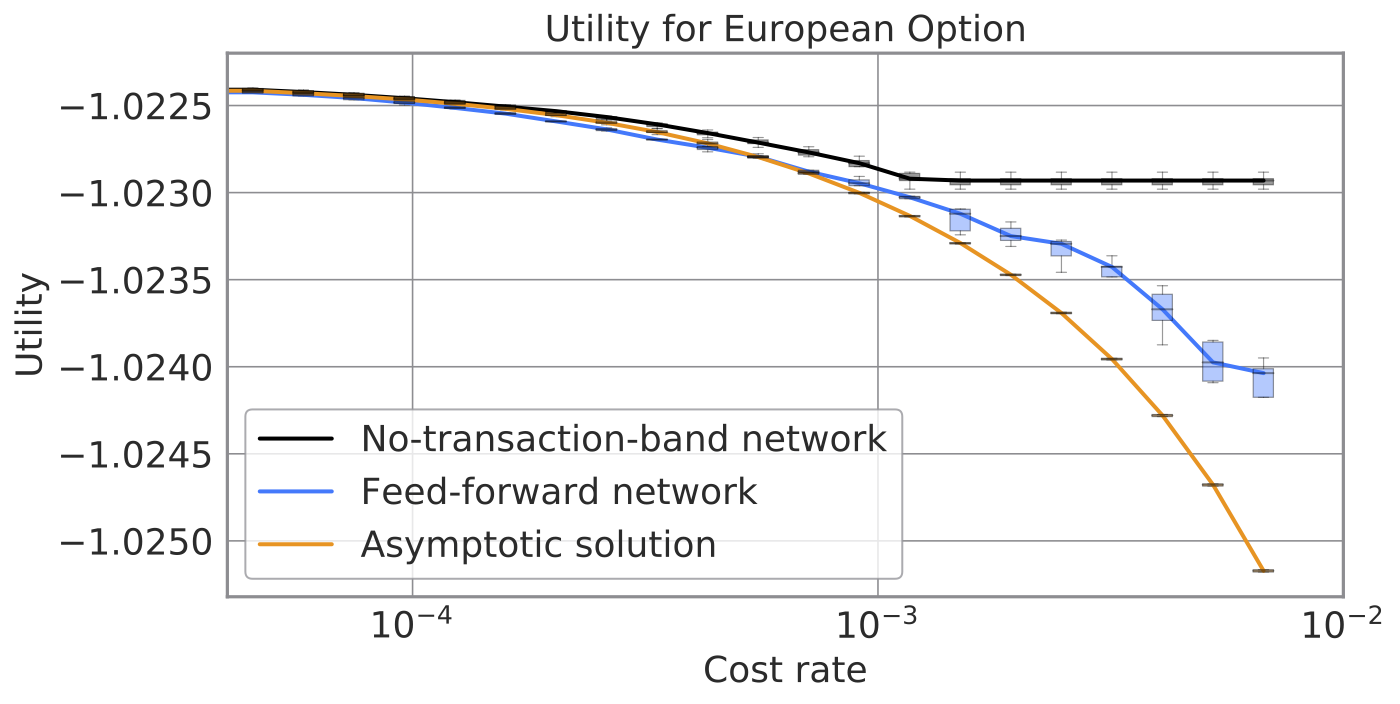
次の図は、ヨーロピアン・オプションに対して各方法が実現する効用を、コスト率の関数として示したものです。幅広いコスト率に対し、No-Transaction Band 戦略がもっとも高い期待効用を実現します。コストがある閾値を超えると期待効用が下げ止まるのは、No-Transaction Band ネットワークが取引コストが高すぎる場合にあえてヘッジしないことを学習するためで、この利点は他の手法ではみられません。
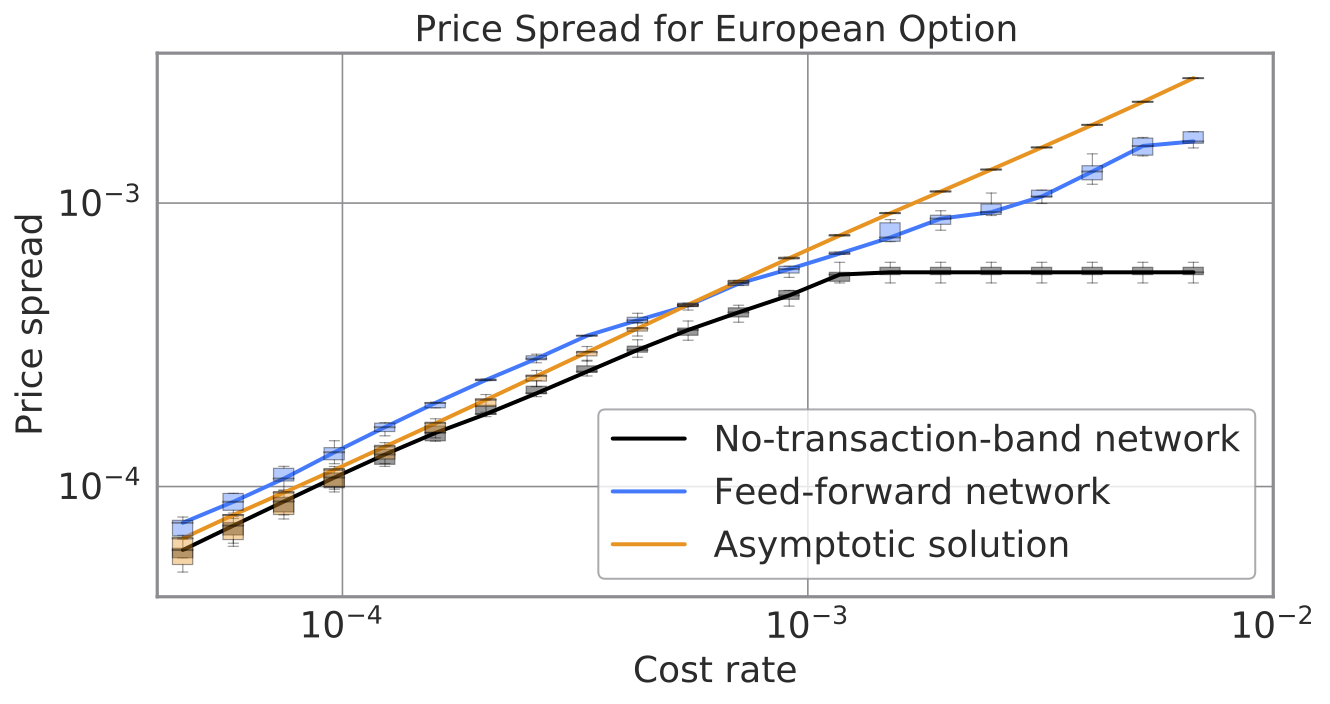
また、デリバティブの価格づけを行いました。価格づけの理論は割愛しますが、実務的には証券会社が顧客に請求するデリバティブ代金に対応するため、安いほど望ましいです。No-Transaction Band ネットワークは、他の方法に比べ最大で数 % 安い価格を実現します。この価格差は証券会社と顧客へもたらされる利益となり、デリバティブ市場の流動性にも貢献します。
No-Transaction Band ネットワークは、”解析解”よりも安い価格を実現しています。解析解はコスト率についての主要項のみを残す近似をする一方、No-Transaction Band ネットワークは高次の寄与まで考慮できているより安い価格を得られた、と私たちは解釈しています。ここで考えている価格の真値は “あらゆる戦略について達成しうる値の最小値” として定義されるので、最も安い No-Transaction Band ネットワークの価格が最も正確です。
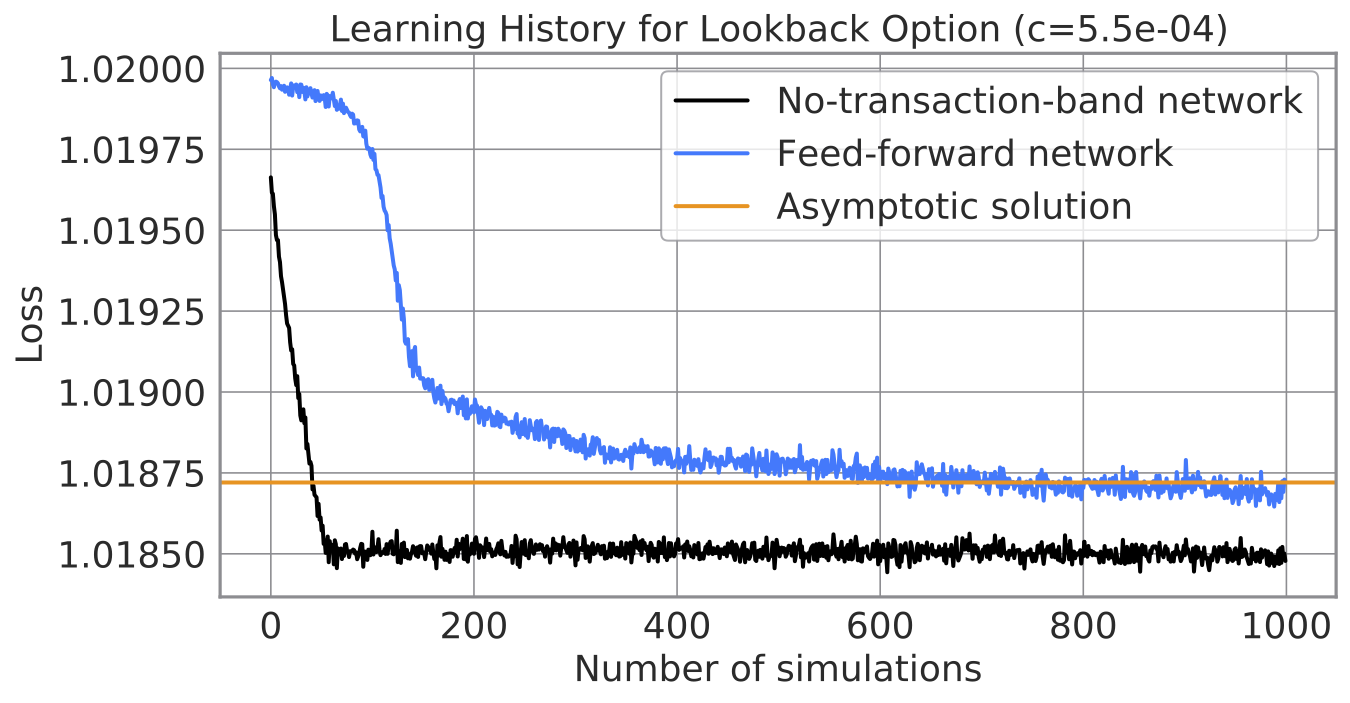
ルックバック・オプションについても結果は同様です。ルックバック・オプションは経路依存性をもつ複雑なデリバティブですが、ヨーロピアン・オプションと同程度の時間で学習が完了します。この結果は、我々の方法がより複雑なデリバティブへもスケールすることを示唆します。
成果
研究成果を「効率的なDeep Hedgingのためのニューラルネットワーク構造」として人工知能学会(SIG-FIN)で発表し、2020 年度人工知能学会研究会優秀賞を頂くことができました。大変光栄に感じています。また、より詳しい論文を “No-Transaction Band Network: A Neural Network Architecture for Efficient Deep Hedging” として公開しました。
Google Colab 上で No-Transaction Band の性能を体験するためのミニマルな実装を GitHub リポジトリ pfnet-research/NoTransactionBandNetwork で提供しています。
また、PyTorch に基づく Deep Hedging の汎用ライブラリ pfhedge を公開しました。次のような直感的なコードで Deep Hedging を実装できます。このライブラリが、Deep Hedging によるデータ駆動のデリバティブ事業に向けた研究開発を加速することを期待しています。
from pfhedge import Hedger
from pfhedge.instruments import BrownianStock, EuropeanOption
from pfhedge.nn import MultiLayerPerceptron
derivative = EuropeanOption(BrownianStock(cost=1e-3))
hedger = Hedger(MultiLayerPerceptron(), features=["moneyness", "expiry_time", "prev_hedge"])
hedger.fit(derivative)
hedger.price(derivative)
さいごに
No-Transaction Band ネットワークは、従来手法よりも圧倒的に高速に最適ヘッジ戦略を学習します。証券会社は、人的コスト・取引コストを自動化によって削減しながら、最善のプライスを迅速に提供して顧客のニーズを満たすことができます。また、コスト効率的な取引戦略は市場インパクトが生じるような大口執行を可能にするため、証券会社と顧客により大きな付加価値を創出し、デリバティブ市場の流動性に貢献します。Deep Hedging の実用上の課題はまだ多いものの、最も大きな障壁のひとつを乗り越え、テクノロジーによる金融業の発展に貢献できたことを誇りに思います。
No-Transaction Band ネットワークのアイデアは、深層学習のボトルネックを念頭におきながら、取引コスト下の定量ファイナンスに関する由緒ある理論を拡張することで得られました。卓越したアイデアを追求するために、異なる視点を柔軟に結びつけることが重要であると実感しました。
この成果を可能にしたのは、共同研究者の皆様による惜しみないサポートと、Preferred Networks の強力な計算環境です。いもすさんには深層学習を円滑に進めるための改善法を親身にご提供頂きました。伊藤さんには定量ファイナンスの知見や文献を多数共有いただき大変勉強になりました。南さんには主に理論面で心強いサポートを頂いたほか、明晰な論文を書くための強力な手助けを頂きました。野村アセットマネジメントの中川さんには研究開発だけでなく実務面のフォローアップも頂くことができ大変頼りになりました。また、試行錯誤を伴う研究開発には Preferred Networks の潤沢な計算資源が不可欠でした。時間・資源・環境を惜しみなく提供いただいた Preferred Networks・野村アセットマネジメント両社に深く感謝します。
文献
- Shota Imaki, Kentaro Imajo, Katsuya Ito, Kentaro Minami and Kei Nakagawa, “No-Transaction Band Network: A Neural Network Architecture for Efficient Deep Hedging”. arXiv:2103.01775 [q-fin.CP], Available at SSRN: https://ssrn.com/abstract=3797564
- 今木翔太, 今城健太郎, 伊藤克哉, 南賢太郎, 中川慧, “効率的な Deep Hedging のためのニューラルネットワーク構造”, 人工知能学 金融情報学研究会(SIG-FIN)第 26 回研究会.
- Hans Bühler, Lukas Gonon, Josef Teichmann and Ben Wood, “Deep hedging”. Quantitative Finance, 2019, 19, 1271–1291. arXiv:1609.05213 [q-fin.CP].