こんにちは。エンジニアのいもす (今城 健太郎) です。現在、投資ファンドを作るため金融時系列の予測モデルの研究開発を行っています。その予測モデルについて、PFN の今城健太郎・南賢太郎・伊藤克哉と野村アセットマネジメント株式会社の中川慧氏が共同で執筆した論文が、人工知能分野における世界トップクラスの国際会議である AAAI 2021 に採択されました。

今回採択された論文 Deep Portfolio Optimization via Distributional Prediction of Residual Factors では、深層学習を用いたポートフォリオ最適化を、様々な金融時系列の性質を帰納バイアスとして導入することで改善する手法を提案しました。本記事では、深層学習のモデル設計という観点でどのような面白さがあるかに触れつつ、採択論文について簡単に紹介します。

はじめに: 帰納バイアスの導入

深層学習によって世の中の様々な問題の性能改善が行われており、とりわけ画像分野においての性能改善が顕著です。深層学習は複雑なパターンを見つけ出す能力があると言われたりしています。しかし実際には構造のあるパターン（例えば繰り返し構造であったり次元間の関係性の共通パターンであったり）を発見するのは苦手であり、画像に関してうまくいく理由は「畳み込みニューラルネットワーク」と呼ばれる構造が、画像とは何かという「帰納バイアス」（データがどのような性質を満たすかという制約）を効率よく深層学習モデルに与えているからだと私は考えています。

本研究では、金融時系列の予測問題を取り扱い、深層学習を用いたよりよい取引戦略の設計を目指します。

一般に、金融時系列を予測するのは、非常に難しい問題であると言われています。まず、金融分野で広く信じられている基本的な事実として、市場は「儲からないように」、つまり予測ができないように動いています。これは、機械学習の手法を適用するにあたって通常要求されるような、定常性などといったよい性質を仮定できないということを意味します。加えて、金融時系列のタスクでは、他の機械学習タスクと比べても訓練データが不足しがちです。例えば、1 銘柄を 1 画像と見立てるならば、データは多くても数百枚しか手に入りません。

そのような中で市場に存在する歪み（収益機会）を見つけていく必要があるのですが、愚直にチャートパターンを探そうとすると、探索空間が広すぎるために汎化する前に過学習に陥ってしまい、市場の歪みを十分に捉えきれません。

これらをふまえて本研究では、金融時系列の予測可能性の向上に寄与するような金融時系列特有の性質について考察し、それをいかにして深層学習モデルへ取り込むかについて提案を行いました。具体的には、

1. 残差項（個別銘柄特有の変動）の効率的な抽出
2. 金融時系列の振幅不変性・時間スケール不変性を考慮したネットワークアーキテクチャの提案
3. 分布予測によるポートフォリオ構築

の 3 つの要素技術の提案を行い、株取引における性能が向上することを確かめました。これらはいずれも、金融分野で研究されてきたドメイン知識を帰納バイアスとして機械学習モデルに取り組む手段を提供しているといえます。

残差項の効率的な抽出

本研究の 1 つ目の貢献は、株のリターン（株価の変動率）の時系列から、残差項と呼ばれる各銘柄の特有の変動を効率的に抽出する手法を提案したことです。

各銘柄の価格変動は、マーケット全体の変動（例えば TOPIX や日経平均株価のような変動）をはじめとした、複数の銘柄間に共通する因子（共通項）から大きな影響を受けています。したがって、もし各銘柄の価格変動をそのまま入力として深層学習モデルに取り込んだ場合、モデルはマーケット全体に追従するような変動に偏って学習してしまう可能性があります。一方、どの銘柄を取引すべきかの意思決定を行うには、各銘柄における「固有の動き」を学習できることが望ましいです。そして、それは共通項を取り除いた残りの変動として現れると考えられます（これを残差項と呼びます）。よって、マーケット全体の変動に対する過学習をすることなく、残差項を効率的に学習する手法の設計が重要です。

まず、仮に残差項が抽出できたとして、それが予測や取引戦略にどのように役立つかについて確認してみます。図 1 は、米国株において、代表的ないくつかの銘柄の生リターンを集めたもの (raw returns)、および、残差項に相当する因子を抽出したもの (FA residuals, PCA residuals) に対して、リバーサル戦略と呼ばれる簡単な戦略を適用したときの累積リターンをプロットしたものです。残差項を抽出することで一貫して性能が向上していることから、残差項にも予測可能性が残っているということが示唆されます。また、特筆すべき点として、残差項を抽出することによって、いくつかの有名な金融危機の影響を緩和できていることが確認できます。これは、残差項がマーケット全体よりも各銘柄の固有の変動を表しているということを反映しています。

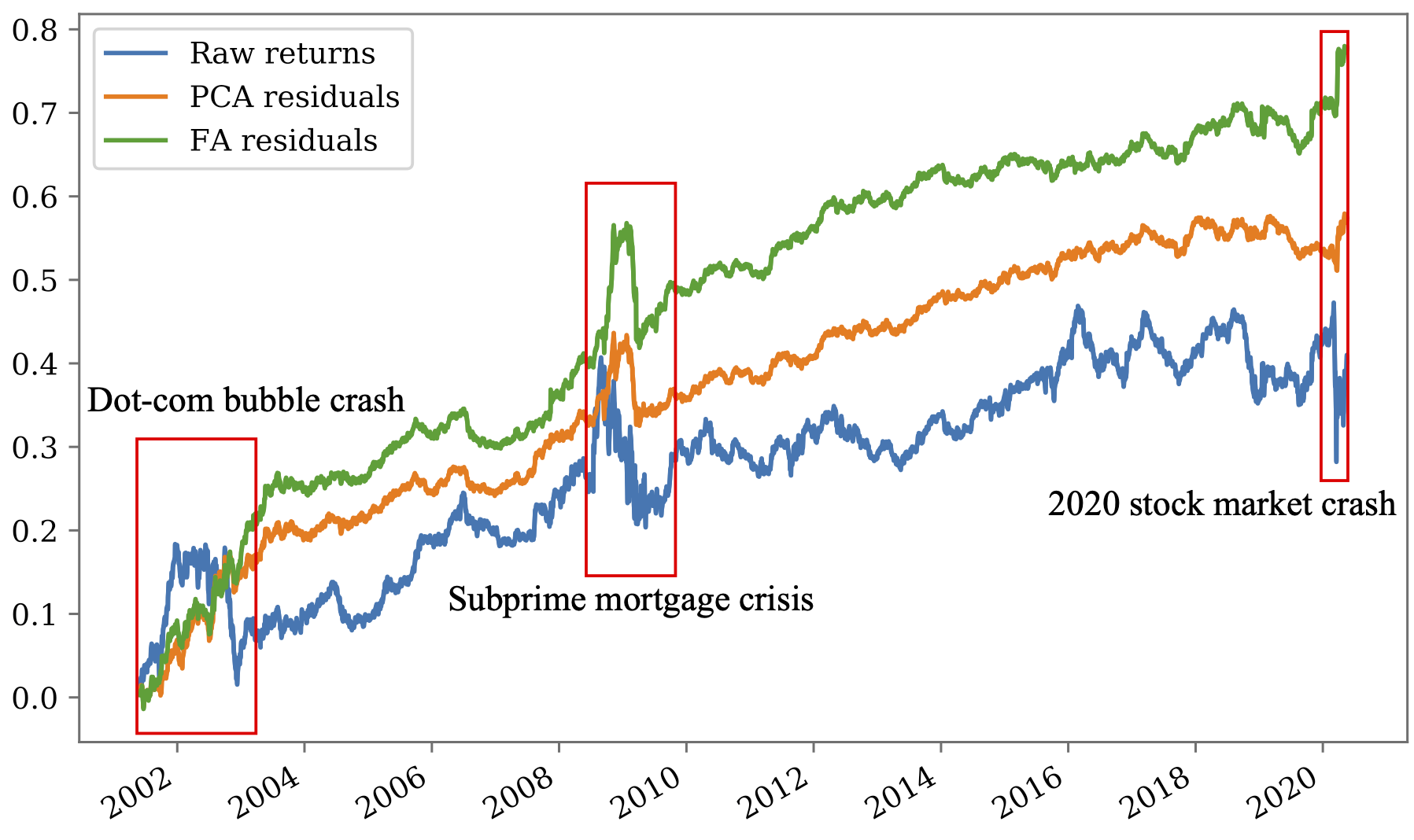
図 1: 残差項の上でリバーサル戦略で取引したときの利益の変化

技術的には、共通項・残差項といった概念は、線形因子モデルを仮定した分解によって定義されます。通常、このような分解は因子分析 (FA) を利用して行われますが、一般に FA は非常に時間がかかる処理であり、深層学習におけるデータ前処理の手段としてはコストが高くついてしまいます。本研究では、より単純かつ FA よりはるかに高速に計算できる主成分分析 (PCA) を利用することで、実用に耐える計算時間で共通項を除去することができることを実験および理論の両面で明らかにしました。

振幅不変性・時間スケール不変性

図 2 のような図をローソク足チャートといい、ある一定期間の株価の変動を表しています。図 2 では、縦軸（振幅）および横軸（時間）のスケールを意図的に隠してあります。さて、このようなチャートを見せられたとき、もとはどのようなスケールだったか予想はつくでしょうか。

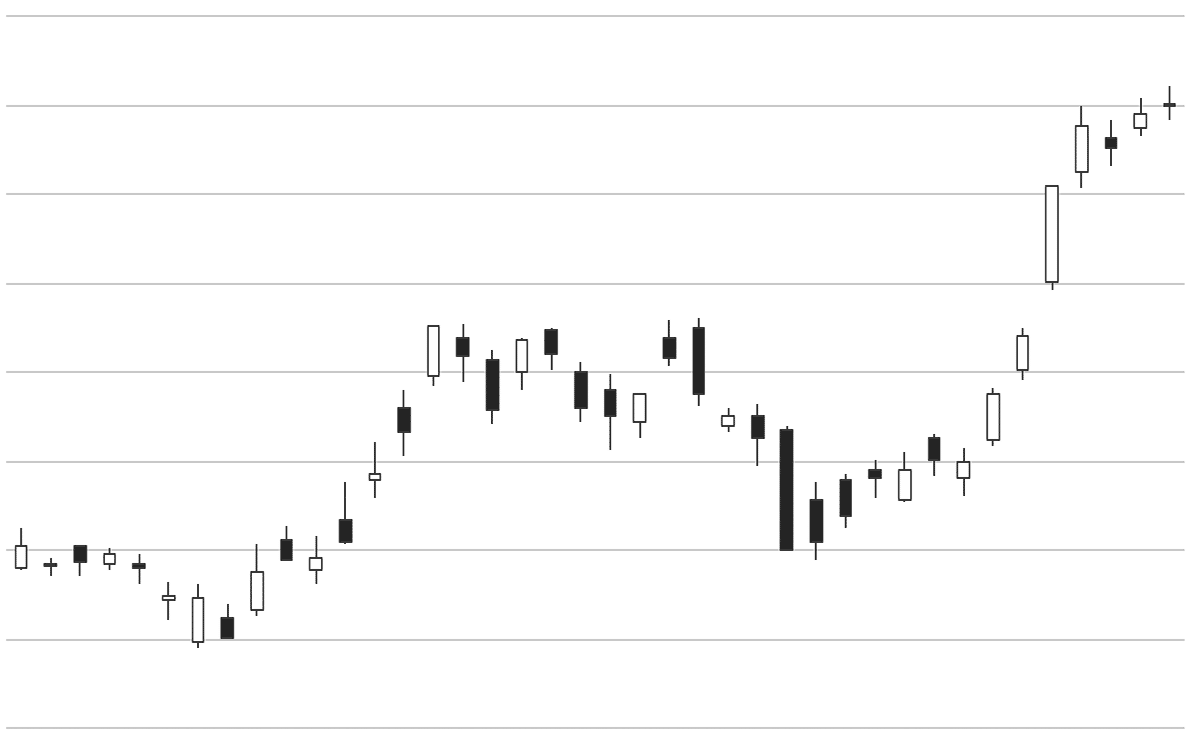
図2: ローソク足チャートの例（これの横軸と縦軸のスケールは想像つきますか？）

もし、スケールを隠したチャートからもとのスケールを簡単に復元できないのだとしたら、金融時系列予測において、振幅や時間のスケールの情報はそれほど大事ではない可能性があります。言い換えれば、金融時系列において、データは振幅や時間に関してある種のスケール不変性をもっているといえます。

本研究の 2 つ目の貢献は、金融時系列におけるスケール不変性の構造を考慮したネットワークアーキテクチャの提案です。深層ニューラルネットワークの典型的な設計では、振幅や時間スケールを伸縮させてできるデータは異なる入力として認識しますが、スケール不変性のもとではこれらは同一の情報を保持したデータであるとみなすことができます。したがって、ネットワークの設計において金融時系列特有のスケール不変性を考慮することによって、実効サンプルサイズを向上させることができ、学習効率が改善される可能性があります。

そこで本研究ではまず、振幅不変性のために入出力を入力の振幅のスケールで割ることにより正規化する構造を導入しました。これにより縦軸のスケールが異なるだけの入出力データを深層ニューラルネットワークが同様に扱うようになりました。次に、時間スケール不変性のために畳み込みのような構造 (図 3) を導入しました。この構造は異なる時間スケールに伸縮させた入力データを同じネットワークに流すため、金融時系列予測のために捉えたい特徴が訓練データに様々な時間スケールで現れていたとしても、効率的に捉えられるようになりました。実際に、これらの構造を利用することで、実世界の株価データの上での性能が大きく改善できることを確認しました。

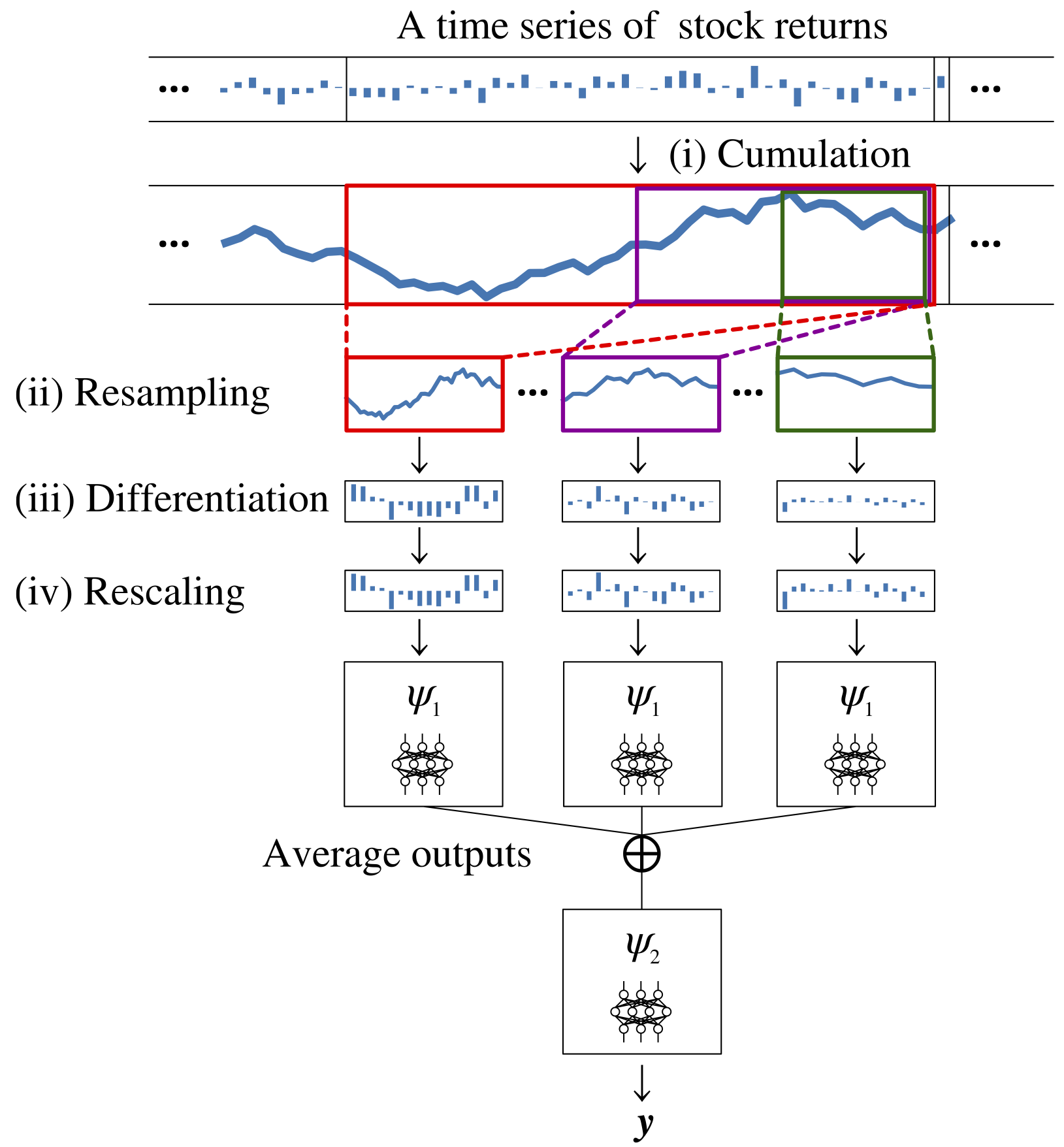
図 3: 時間スケール不変性が学習できる深層学習モデルの構造

分布予測によるポートフォリオ構築

株価予測の最終的な目的は安定的な取引戦略の構築であるため、単純に価格（またはリターン）自体を予測するだけでなく、リターンがどの程度大きく「ぶれる」可能性があるか（つまりリスク）の情報が重要になります。特に、取引戦略やポートフォリオを評価する際には「高い期待リターンを得ることができるが、リスクは小さくとどまるような戦略」がよい戦略であると言えます。このため、通常の回帰分析のように期待値のみを予測するのではなく、将来のリターンの「分布」を予測することが重要です。

そこで本研究では、リターンの残差項の分布を予測するネットワークを構築し、予測された分布の情報に基づいてポートフォリオを設計する手法を提案しました。分布の形状を予測する具体的な手段としては、分位点回帰 (quantile regression) に基づく手法を採用しています。この提案の背景としては、株式のリターンの分布は、歪度が大きく（＝左右非対称である）、裾が重い（＝外れ値的に大きな値もそれなりの頻度で出現する）といった性質をもつことが経験的に知られているということがあります。そこで、正規分布のように左右対称かつ裾が軽い分布族をフィットさせるよりも、分位点回帰に基づく予測のほうが正確な情報を抽出できる可能性があります。実際に、論文では実データにおける実験において有用性が確認されました。

まとめ

本記事では、AAAI 2021 に採択された論文の重要な 3 つのアイデアについて簡単に紹介しました。記事では紹介できませんでしたが、論文では、日本株と米国株の過去の時系列を用いて、提案した手法により予測可能性が高まることを示しました。また、それぞれの要素技術を取り除いたモデルとの性能を比較することで、提案したいずれの要素技術も予測可能性を高められる要素になることを実験により確かめました。興味のある方は、ぜひ元論文を参照してみてください。

PFN では今後も金融時系列の様々な性質を取り入れたモデルを開発し予測精度を高めていきます。また同時に投資ファンドに適した投資戦略モデルの開発も推し進めていきます。