Blog
この記事は、2024年夏季インターンの趙欣愷さん、エンジニアの小田啓太、リサーチャーの岩澤諄一郎、徳岡雄大による寄稿です。
概要
- 医用画像に対する従来のメンバーシップ推論攻撃 (Membership Inference Attacks; MIA) は、医用画像固有の再構成の難しさや拡散モデルの周波数成分ごとの再構成能力の限界により、精度に課題がありました。
- 我々の提案手法「Frequency-Calibrated Reconstruction Error (FCRE)」は、ラプラシアンスコアを用いた周波数ベースの難易度キャリブレーションと、画像の構造的類似度 (SSIM) および再構成誤差を組み合わせたメンバーシップ判定により、従来手法を上回る精度を達成しました。
- 本研究の成果は、医用画像を用いた拡散モデルのプライバシー脆弱性を明らかにし、より安全な医療AI技術開発に貢献することが期待されます。
- 本研究の成果をまとめた論文は、医用画像系トップカンファレンスである MICCAI 2025 のworkshop (DGM4MICCAI) に採択されました。
はじめに
近年、拡散モデルは目覚ましい発展を遂げ、特に医用画像生成のような機微な領域での活用が期待されています[1]。その一方で、学習データに関するプライバシー漏洩のリスクも指摘されています[2,3]。特定の画像がモデルの学習に使用されたかどうかを判定するメンバーシップ推論攻撃 (Membership Inference Attacks; MIA) は、こうしたプライバシーリスクを定量化する上で重要な手法です[4]。
拡散モデルに対するMIAの初期の研究では、画像の復元処理における損失関数の値を比較していました[5]。一方で、近年提案されている最先端のMIA手法では、DDIM (Denoising Diffusion Implicit Models) という拡散モデルの特性を利用しています[6,7]。DDIMでは、画像にノイズを加えてから、再びノイズを除去して元の画像を復元するというプロセス(拡散過程と逆拡散過程)をたどります (図1)。このとき、訓練に使われた画像は、使われなかった画像に比べて、より正確に元の姿に復元されるという性質があります。この性質を利用して得られた誤差画像をピクセルレベルで分析することで、高い精度でメンバーシップ (学習に利用されたデータ) の判定を行うことができます。しかし、このアプローチを医用画像に直接適用するにはいくつかの課題が存在します。
本記事では、医用画像の特性と拡散モデルが抱える課題を踏まえ、医用画像における高精度なMIAの実現を目指して我々が提案した新手法 “Frequency-Calibrated Reconstruction Error (FCRE)” と、その有効性を実験的に示した論文 “Frequency-Calibrated Membership Inference Attacks on Medical Image Diffusion Models” について解説します。
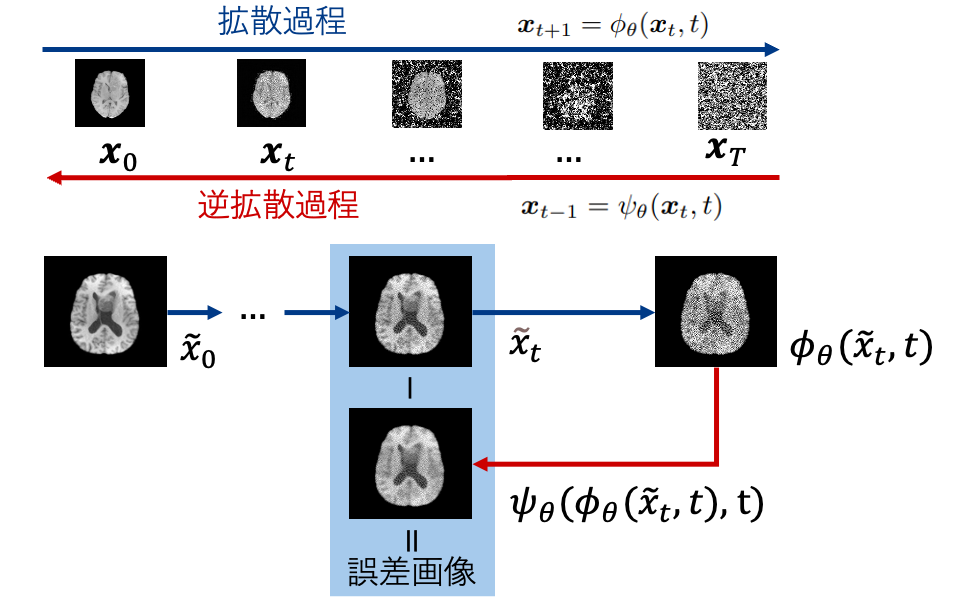
図1. 拡散モデルを用いたメンバーシップ推論攻撃 (Membership Inference Attacks; MIA) における概念図。拡散過程と逆拡散過程において得られた誤差画像を用いてメンバーシップの判定を行う。
医用画像におけるMIAの難しさ
自然画像を対象としたMIAは大きな成功を収めていますが、これをMRIやX線のような医用画像にそのまま適用しようとすると、性能が著しく低下してしまいます。その主な原因は、医用画像が持つ特有の周波数特性にあります。自然画像が主として中程度の周波数成分で構成されているのに対して、医用画像は高周波成分と低周波成分に偏った周波数分布を示す傾向があります。
具体的には、臓器の輪郭といったシャープで詳細な部分を表す高周波数成分と、画像の大部分を占める広大な背景領域を表す低周波数成分に分かれます。ピクセル間の変化が激しい高周波成分は、復元プロセスにおいて大きな誤差を生みやすく、これがMIAの判断を狂わせるノイズとなってしまいます (図2)。その一方で、変化の乏しい低周波成分は、訓練データであってもなくても復元誤差が小さく、両者の違いを判別するための有益な手がかりになりにくくなります。
さらに、この周波数特性の問題に加えて、「画像の復元の難しさ」という本質的な課題も存在します。もともと複雑な構造を持つ画像は、モデルが訓練で見たことがあるかどうかに関わらず、きれいに復元すること自体が困難です。従来のMIAは、復元誤差の大きさのみを判断基準としていたため、このような「本質的に復元が難しい非訓練データ」を、「復元に失敗した訓練データ」と誤って分類してしまうという深刻な課題を抱えていました。つまり、復元誤差という単一の指標だけでは、画像のメンバーシップを正確に判断するには不十分だったのです。
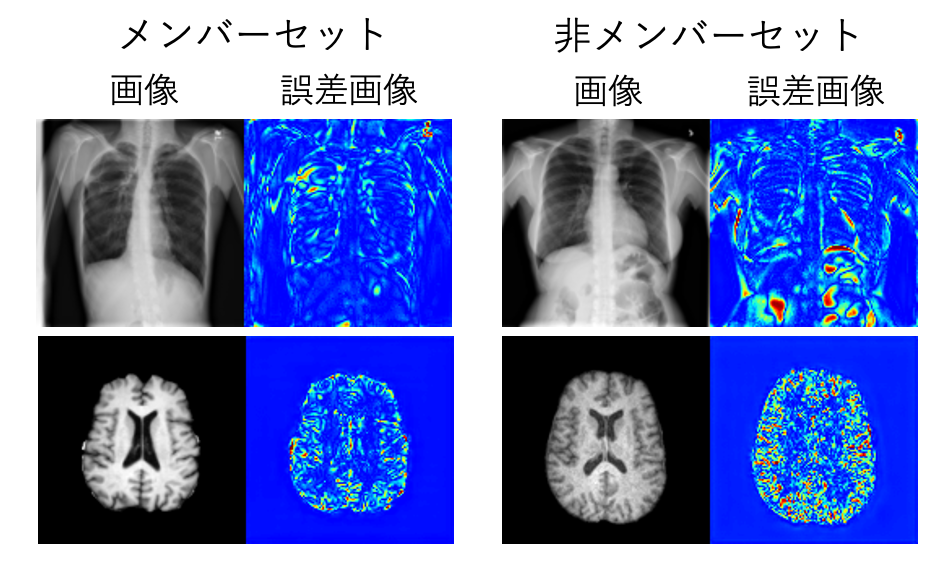
図2. メンバーセットと非メンバーセットにおける画像とDDIMにより得られた誤差画像の比較。
提案手法:Frequency-Calibrated Reconstruction Error (FCRE)
これらの課題に対処するため、本論文ではFCREという新しいアプローチを提案しています。FCREの核心は、画像の特定の周波数帯域 (中間周波数帯域) における再構成誤差に着目する点にあります。具体的には、以下のステップでメンバーシップを推論します。
- ステップ1: 周波数に基づいた難易度キャリブレーション:
- 画像のパッチごとにラプラシアンスコアを用いて難易度スコアを計算
- 高周波数 (再構成が困難) および低周波数 (情報量が少ない) 領域を除外してメンバーシップ判定に有効な中間周波数帯域のパッチを選択
- ステップ2: 構造的類似度と再構成誤差に基づくメンバーシップ推論:
- 選択された中間周波数帯域において、元画像と再構成画像の構造的類似度 (SSIM) と再構成誤差 (L2 loss) をそれぞれ計算して組み合わせることでMIAスコアを算出
- 算出された MIA スコアを用いた閾値処理によりメンバーシップを判定
この周波数選択的なアプローチにより、FCREは画像の難易度の影響を軽減し、メンバー画像と非メンバー画像をより明確に区別することが可能になります。
実験と結果
提案手法FCREの有効性を検証するために、脳MRIデータセット FeTS 2022、胸部X線データセット Chest X-ray8、そして自然画像データセット CIFAR-10 を用いた実験を行いました。
- FeTS 2022 [8]
- 複数の医療機関から収集された脳MRIデータセット。メンバーセットとして16機関から収集した740症例を、非メンバーセットとして学習に使用していない特定の1機関から収集した511症例を利用。各3D MRI T1 強調画像から50枚のスライスを抽出し、メンバー画像を37,000枚、非メンバー画像を25,600枚に分割。
- Chest X-ray8 [9]
- 胸部X線画像データセット。メンバーセット用に3,600枚以上、非メンバーセット用に同じく3,600枚以上の画像をそれぞれランダムに抽出。
- CIFAR-10 [10]
- 自然画像データセット。それぞれ25,000枚の画像を含むメンバーセットと非メンバーセットに分割。
医用画像データセット (FeTS 2022、Chest X-ray8) において、FCRE は既存の MIA 手法 (Loss-based、SecMI、PIA/PIANなど) を一貫して上回る性能を示しました (表1)。これは、FCREが医用画像の微細な周波数情報を効果的に捉え、メンバーシップ判定の精度を大幅に向上させることを示しています。また、L2 loss のみを使用するFCRE (L2) と、L2 loss と SSIM を組み合わせたFCRE (L2+SSIM) を比較した結果、FCRE (L2+SSIM) の方が優れた性能を示し、SSIMのような構造的類似度も同時に評価する重要性が確認されました。自然画像 (CIFAR-10) においては、TPR1% 以外の指標において FCRE (L2) が最も高精度であり、本手法が汎用的であることが示されました。
また、これらの手法において実際にメンバーシップ判定を行う際のMIAスコアを分布として可視化して比較しました (図3)。SecMI や PIA と比較して、FCRE をもちいたMIAスコアはメンバーセットと非メンバーセットのスコア分布の重なりが大幅に減少し、より明確にメンバーシップ判定が行えることが定性的にも確認することができます。
| Medhod | FeTS 2022 | Chest X-ray8 | CIFAR-10 | ||||||
| ASR | AUC | TPR1% | ASR | AUC | TPR1% | ASR | AUC | TPR1% | |
| Loss-based [5] | 0.554 | 0.428 | 0.001 | 0.521 | 0.390 | 0.003 | 0.738 | 0.804 | 0.049 |
| SecMI [6] | 0.734 | 0.708 | 0.052 | 0.856 | 0.907 | 0.176 | 0.774 | 0.839 | 0.085 |
| PIA [7] | 0.787 | 0.825 | 0.061 | 0.587 | 0.601 | 0.000 | 0.809 | 0.878 | 0.156 |
| PIAN [7] | 0.786 | 0.811 | 0.078 | 0.590 | 0.604 | 0.000 | 0.800 | 0.849 | 0.291 |
| FCRE (L2) | 0.835 | 0.898 | 0.185 | 0.914 | 0.958 | 0.316 | 0.810 | 0.880 | 0.162 |
| FCRE (L2+SSIM) | 0.853 | 0.926 | 0.328 | 0.926 | 0.971 | 0.409 | 0.778 | 0.840 | 0.085 |
表1. 各データセットにおけるMIA精度比較。ASR: Attack Success Rate, AUC: Area Under the ROC Curve, TPR1% : True Positive Rate at 1% False Positive Rate
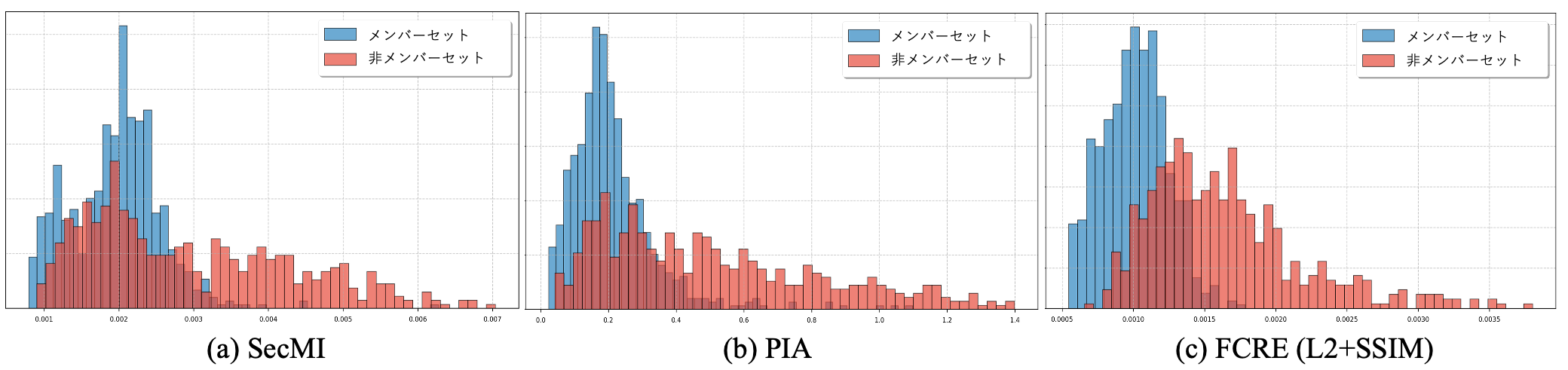
図3. 各手法における MIA スコア分布の比較。検証には FeTS 2022 データセットを用いている。
FCRE の周波数帯域の選択における難易度キャリブレーションでは、極端に低い周波数帯域 (15%以下) と高い周波数帯域 (85%以上) を除外しています。そこで、FCRE の有効性を確認するために、周波数帯域の選択に関するアブレーション検証を行いました (表2)。その結果、極端に低い周波数帯域と高い周波数帯域を除外し、適切な中間周波数帯域を選択することの重要性が確認されました。これらの結果から、どちらか片方の周波数帯域のみを除外した場合でも精度は向上するものの、極端な周波数帯域の情報はMIAにとってノイズになる可能性が示唆されました。
| Lmin | Lmax | FeTS 2022 | Chest X-ray8 | ||||
| ASR | AUC | TPR1% | ASR | AUC | TPR1% | ||
| 0% | 100% | 0.791 | 0.861 | 0.144 | 0.820 | 0.877 | 0.227 |
| 15% | 85% | 0.853 | 0.926 | 0.328 | 0.926 | 0.971 | 0.409 |
| 15% | 100% | 0.791 | 0.861 | 0.144 | 0.820 | 0.883 | 0.227 |
| 0% | 85% | 0.818 | 0.882 | 0.254 | 0.928 | 0.968 | 0.328 |
表2. 周波数帯域の選択がメンバーシップ推論に与える影響。Lmin は低周波数帯域の閾値、Lmax は高周波数帯域の閾値をそれぞれ表している。
まとめと今後の展望
本論文で提案されたFCREは、医用画像拡散モデルに特化した新しいメンバーシップ推論攻撃手法であり、周波数に基づいた難易度キャリブレーションを導入することで、既存手法の限界を克服しました。この研究は、特に機微な患者データを扱う医用画像の文脈において、拡散モデルのプライバシー脆弱性を浮き彫りにするとともに、実用性とセキュリティのバランスが取れた、より堅牢なプライバシー保護型生成モデルのさらなる研究開発を促すものだと考えます。今後、データセットごとに最適な周波数帯域を自動的に決定する適応的な閾値設定方法などの研究が進むことで、FCREアプローチの堅牢性と汎用性がさらに向上することが期待されます。提案手法の詳細を知りたい方は、論文 (https://arxiv.org/abs/2506.14919) の方もぜひご覧ください。
最後に、Preferred Networksでは採用を行っております。今回の記事で興味を持っていただけた方はぜひご応募ください。
- Healthcare and Wellness Project Development Engineer・Researcher/ヘルスケア・ウェルネスプロジェクト 開発エンジニア・リサーチャー
- Machine Learning・Optimization・Data Science Engineer/機械学習・最適化・データサイエンスエンジニア
- LLM Service Development Engineer/基盤モデルサービス開発エンジニア
- ビジネス開発(ソリューションビジネス)
- その他の募集職種
参考文献
[1] Kazerouni, A., et. al. Diffusion models in medical imaging: A comprehensive survey. Medical Image Analysis 88, 102846 (2023)
[2] Akbar, M.U., et. al. Beware of diffusion models for synthesizing medical images—a comparison with GANs in terms of memorizing brain MRI and chest X-ray images. Machine Learning: Science and Technology 6(1), 015022 (2025)
[3] Wang, S., et. al. A semantic conditional diffusion model for enhanced personal privacy preservation in medical images. IEEE Journal of Biomedical and Health Informatics (2024)
[4] Shokri, R.,et. al. Membership inference attacks against machine learning models. In: 2017 IEEE symposium on security and privacy (SP). pp. 3–18. IEEE (2017)
[5] Matsumoto, T., et. al. Membership inference attacks against diffusion models. In: 2023 IEEE Security and Privacy Workshops (SPW). pp. 77–83. IEEE (2023)
[6] Duan, J., et. al. Are diffusion models vulnerable to membership inference attacks? In: International Conference on Machine Learning. pp. 8717–8730. PMLR (2023)
[7] Kong, F., et. al. An efficient membership inference attack for the diffusion model by proximal initialization. arXiv preprint arXiv:2305.18355 (2023)
[8] Pati, S., et al. The federated tumor segmentation (FeTS) challenge. arXiv preprint arXiv:2105.05874 (2021)
[9] Wang, X., et. al. Chestx-ray8: Hospital-scale chest x-ray database and benchmarks on weakly-supervised classification and localization of common thorax diseases. In: Proceedings of the IEEE conference on computer vision and pattern recognition. pp. 2097–2106 (2017)
[10] Krizhevsky, A., et al. Learning multiple layers of features from tiny images (2009)
Area