Blog
本記事は、2024年夏季インターンシッププログラムで勤務された榎本倫太郎さんによる寄稿です。
はじめに
2024年度のPFN夏季インターンに参加した、早稲田大学基幹理工学研究科の榎本倫太郎と申します。学部では、大規模言語モデル(LLM)における事前学習コーパスのフィルタリングの研究を行っておりました。「LLMを使ったデータセット自動作成」というテーマに興味を持ち、本インターンシップに参加いたしました。
インターンシップの期間中、LLMの数学的推論タスクの精度を向上させることを目指しました。この目的のために、生成能力が高いLLMによって生成されたデータセットを用いて、対象となる事前学習済みのLLMを教師あり学習(SFT : Supervised Fine-Tuning)し、その結果を評価しました。本来の目的は事前学習でのモデルの性能向上ですが、事前学習の実験を行うには莫大なコストがかかるため、我々は事後学習、特に事前学習と最も関連性のあるデータセットの改良に焦点を当てています。さまざまな問題生成手法を試み、本記事ではデータ合成の工夫と、成功した点や改善が必要だった点について考察を行います。
背景
LLMの事前学習において、自然言語の広範な語彙、文法、文脈を理解させるために、ウェブページや書籍などから大量に収集したテキストデータセットを用います。また、LLMの出力を洗練化したり、特定のドメインやタスクに適応させたりするために追加のデータセットが必要です。例えば、医療、金融、法律などのドメイン特化のものや、一般常識を問うQAタスク形式のものがあります。
今回の調査・研究では英語の数学推論タスクを対象とします。数学推論タスクとは、文字通りLLMに数学の問題を解かせるもので、一般に多段階の論理的な推論が必要な難しいタスクとされています。Huggingfaceでは小学校レベルの算数の文章問題であるGSM8K[1] データセットや、さらに難易度の高い、中高、大学数学レベルのAQUA-RAT [2], MATH [3] データセットなどが公開されています。今回は時間の都合上GSM8Kのタスクのみに着目します。ここでGSM8Kの問題例を一つ挙げます。
- 問題例
James writes a 3-page letter to 2 different friends twice a week. How many pages does he write a year? - 解答例
He writes each friend 3*2=<<3*2=6>>6 pages a week So he writes 6*2=<<6*2=12>>12 pages every week That means he writes 12*52=<<12*52=624>>624 pages a year #### 624
直訳すると、「ジェームズが1週間に2回、2人の異なる友人に3ページの手紙を送るとき、彼は1年で何ページ書くことになるか。」という問題です。人間が解くことは容易ですが、友人1人当たり1週間で何ページ書くか、友人2人ではどうか、1年ではどうかといった具合に段階的に計算する必要があります。LLMは問題文のみ与えられ、最終的な624(ページ)という解答を出力しなければなりません。
今回は最終解答だけでなく、Chain of Thought (CoT) Prompting [4] に代表されるような思考過程(数学問題における途中式のようなもの)も学習します。つまり、問題文の入力に対し思考過程を含めた解答を生成していき、その解答部分のみCross-entropy Lossを計算します。
先行研究として、数学問題の合成データセット作成に関する論文である「Common 7B Language Models Already Possess Strong Math Capabilities」 [5] を紹介します。以降はこの論文をCommon 7Bと呼びます。Common 7Bでは、GSM8KやMATHのオリジナル問題をもとに、生成能力の高いOpen AIのGPT4-turbo で類似の新しい問題とその解答を生成しています。このQAセットを大規模合成し、LLaMA2 [6] モデルの事後学習に用いることで数学推論タスクに強いモデルを作成しています。
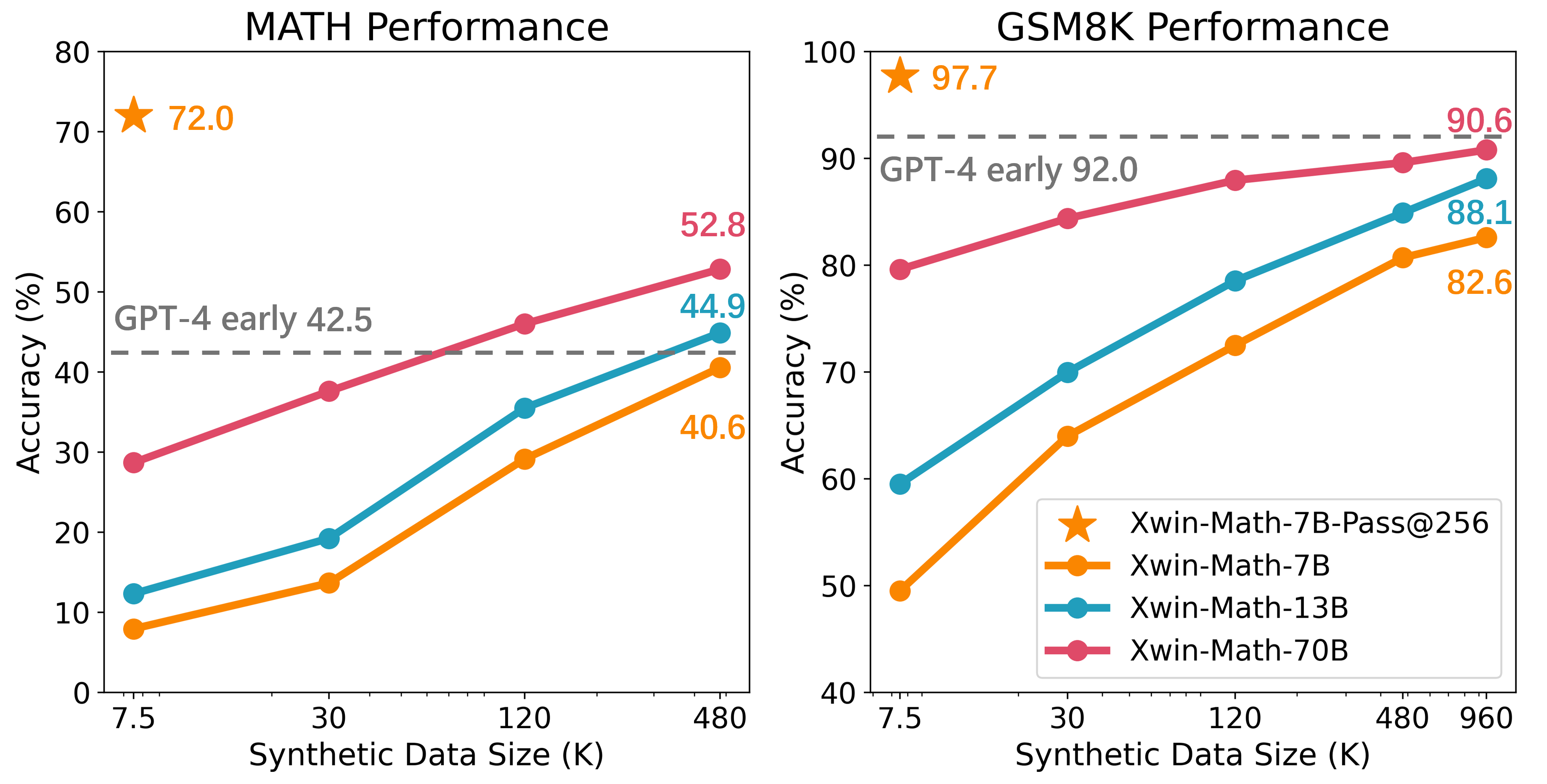
Common 7Bでは、同一の問題に対して解答を確率的に256回推論し、その結果の中に1つでも正答が含まれる可能性をもとに、LLMの数学推論タスクに対する高いポテンシャルを示しています。GSM8Kタスクでは、最大960Kサンプルの合成数学QAデータセットを活用し、LLMの数学推論能力を引き出しています。図からは、合成された学習データセットの量を増やすことで、正答率が単調に上昇していることが確認できます。
Common 7Bが7B以上のモデルで実験しているのに対し、本調査ではより小さな、具体的には1B級のモデルでも大規模化した合成データセットによる学習が有用であるかを調査します。さらに、この精度向上の傾きを増加させるような別の数学問題データセット合成手法を調査します。
実験と考察
実験の概要
問題合成
まずは以降の実験で共通する数学問題の合成手法を説明します。基本的な合成手法はCommon 7Bの論文と同等のものです。
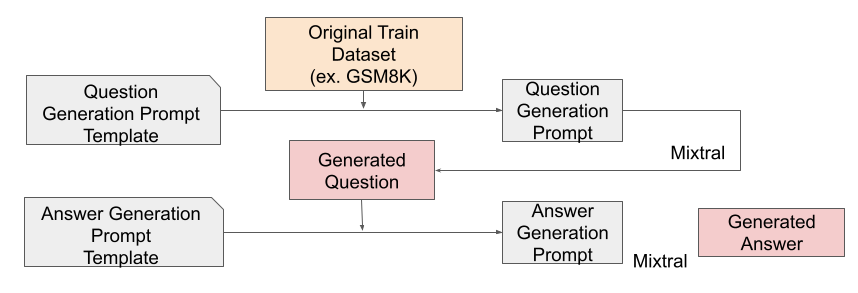
問題生成プロンプトのテンプレートにGSM8Kのオリジナルのtrain用問題を入れます。このオリジナル問題をもとにMistral AIのMixtral-8x22B-Instruct-v0.1を利用し、新しい問題を生成してもらいます。生成された問題に対して別のリクエストでCoT付きの解答を生成してもらいます。この順序で数学QAを大量に生成し、PLaMo-1B事前学習モデル(※)の学習に利用します。各フェーズの詳細は次に示す通りです。
(※)今回の実験で使用したPLaMo-1Bは、PLaMo-Liteとは異なる社内開発用のモデルです。
- 問題生成
生成プロンプトのテンプレートは付録に載せています。基本的にはオリジナル問題をもとに類似した新しい問題を生成するよう命じるシンプルなプロンプトですが、GSM8Kの問題形式に沿うような制限が盛り込まれてます。例えば、解答が設定に対して現実的でない数値になること(7.5人や6.25円など)や複数の答えを求めること(what is the amount of A, B and C?)は禁止しています。これらのルールを上手く適用させるために、一度生成した問題に対して一つのリクエストの中で修正し、修正後の問題も出力するようにしています。 - 解答生成
思考過程と最終解答を得るためにstep-by-stepで解答するように指示しています。また、効率的な評価のために最終回答に数値以外を含めることを禁止しています。 - その他設定
推論時のtemperatureを問題、解答生成ともに1.0に設定しています。これはCommon 7Bの設定と同様で、より多様な問題を生成させるためです。予備実験の結果、解答もtemperatureを下げるとGSM8Kのtestセットでの評価が落ちることが分かりました。この結果は回答の多様性も重要であることを示唆しています。
学習・評価
次に、学習、評価について説明します。合成したデータセットの有用性を示すために、PLaMo-1B事前学習済みモデルをSFTし、lm-evaluation-harness [7] で評価します。
学習設定
- モデル : PLaMo-1B pretrained
- 最大入力トークン : 2048
- 学習率 : 5e-6
- オプティマイザ : AdamW
- 学習率スケジュール : cosine
- エポック数 : 3
1つの学習でV100 (16G) GPUを最大8枚使用して実験を回しました。また、学習は次のように5shotで学習し、GSM8Kのtrainデータセットからランダムに問題解答例としました。
Question: <問題例1>
Answer: <問題例1の解答過程>
#### <問題例1の最終解答>Question: <問題例2>
Answer: <問題例2の解答過程>
#### <問題例2の最終解答>
・
・
・
Question: <問題例5>
Answer: <問題例5の解答過程>
#### <問題例5の最終解答>Question: <答えてほしい問題>
Answer: <解答過程> <- ココ以降を損失計算
#### <最終解答>
損失計算は解答過程と最終解答で行い、解答の過程も学習しています。なお、学習対象のモデルが1Bと比較的小さいのでLoRA [8] などのパラメータ効率の良いファインチューニングは行っておりません。
評価
評価の際はGSM8Kのtestセットの問題を用いて学習時と同様に5shot-CoTで解答を推論し、「####」以降の数値が正答と一致しているか確認します。
基本的には実験の概要のようにGSM8Kの問題を合成し、学習、評価を行っていきます。
合成データセットの大規模化効果
最初にCommon 7B論文の再現実験を行います。実験の概要と同様の手法で合成データセットを評価した結果が次のグラフです。
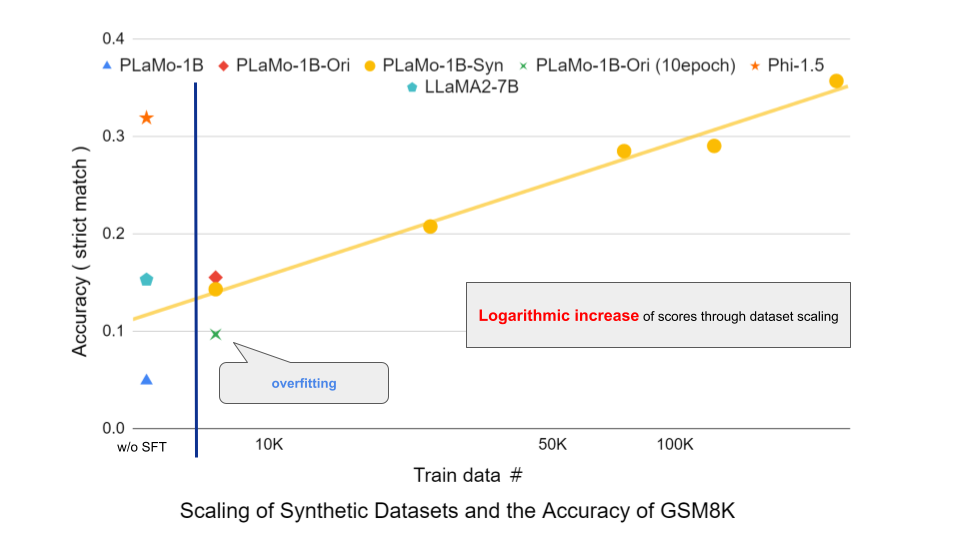
横軸対数のグラフです。凡例の「Ori」はGSM8Kのオリジナルデータで、「Syn」は合成データで学習したモデルの結果を示しています。つまり、黄色のグラフが合成データセットでPLaMo-1Bを学習し、評価した結果です。学習データ量をオリジナルのtrainデータセットと同じ7.4Kサンプルから、250Kサンプルまで増量させています。
SFTなしのPLaMo-1B(青い三角)では5.0%も正答していないのが、合成データ7.4Kでは14.3%と大幅な改善が見られます。この結果は同量のオリジナルデータセットで学習した結果(赤いひし形)やSFTなしのLLaMA2-7Bモデル(緑の五角形)と比較しても競争的です。また、学習データを250Kサンプルまで増加させると、正答率は35.7%とphi-1.5(橙色の星)の結果を超えます。よって、合成データの増量によりGSM8Kの正答率は対数的に増加し、現時点ではその増加は際限がないと言えます。さらに、オリジナルデータのみを10エポック回しても過学習が起きる(緑のばつ)ことも合成データの必要性をサポートしています。
以上でPLaMo-1BというLLMの中では比較的小さなモデルでも、Mixtral-8x22Bのインストラクションモデルで生成された数学問題を用いてSFTすることで精度が改善されることが示され、Common 7Bの再現ができました。このまま増やしても正答率は上昇していきそうですが、スコアの対数的増加に対して合成データを増やしていくのにはコストがかかるため、この増加の割合をさらに向上させるような新しい合成手法を見つけたいです。そこで、いくつかの手法を試しましたが、まずは上手くいった手法を1つ、それから上手くいかなかった手法を紹介したいと思います。
多様で高難易度な数学問題を合成する手法の提案
仮説
データセットの工夫に限るとなると、数学推論タスクでは問題と解答過程の工夫が考えられます。ここで紹介するのは問題をより多様で高難易度にする方法です。
多様な問題
ここでの「多様な」とは、オリジナルの問題から数値や問題文の背景が変化している状態を指します。数学問題の合成手法としては、問題文中の数値を変更したり、問題文自体を大規模言語モデル(LLM)によって言い換えたりする方法が存在します。このような変化を「摂動」と呼び、GSM8Kの派生データセットであるGSM-Plus [9] や、数学推論タスクの向上を目指した合成手法としてのMetaMath [10] が存在します。一般的には、学習データの多様性を高めることで汎化性能が向上し、テストセットへの対応力が強化されます。さらに、学習データセットを合成によって増やすことを考慮すると、その重要性は一層高まります。問題をどの程度まで変化させても良いのかは別途検証が必要ですが、少なくとも学習データの多様性が必要であることは確認しておきます。
高難易度な問題
GSM8Kの問題には2~8ステップの計算を要する問題が含まれています[1]。数学問題で最終解答を間違える原因は途中ステップのどこかで推論ミスが起こっていることなので、解答ステップ数が多くなるほど最終解答が誤答となる確率が高くなります。また、LLMはCoTで問題を解く際に、文章題を適切に解釈し順に計算していく必要がありますが、ステップ数が増加すると問題文を正しく理解するのが難しくなります。したがって、解答ステップ数の多い問題は正答率が落ちます。以下はオリジナルtestセットの解答にある式の数をもとに解答に必要なstep数を推定し、step数ごとの正答率を表したグラフです。
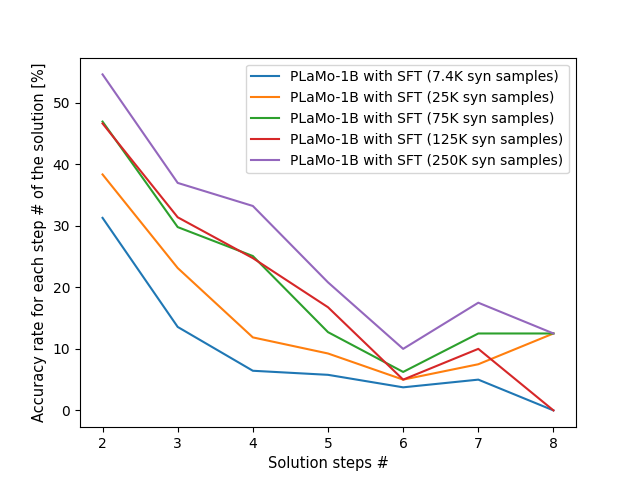
学習に用いる合成データが増えれば、解答ステップ数の少ない問題は順調に精度を向上させているのに対し、step数の多い問題は伸び悩んでいます。高難易度の問題の正答率を上げるために、合成問題のstep数を上げることを考えます。
以上の理由で、多様で高難易度な合成問題がGSM8Kのスコアをさらに伸ばすという仮説を検証します。
手法
手法の説明に入ります。手法といってもシンプルで、問題合成に使用するプロンプトを変えるだけです。Common 7BでのプロンプトはGSM8Kのtrainデータセットからランダムに1問をシード問題とし、「シード問題に類似した新しい問題」をLLMに生成させていました。この方法では、生成時のtemperatureを上げても同じシード問題から生成された合成問題間の問題設定が似ることがあります。そこで、シード問題を二つ与えることにします。同時に、シード問題からさらに解答ステップ数を1 step追加して問題難易度を上げるように指示します。プロンプトの一部を載せます。(プロンプト全体は付録へ)
Question Generation Prompt(……は省略箇所です。)
……
You will be given two math questions, Base Question and Supplementary Question. Please create a new and more challenging question based on the given Questions and following instructions.
……
# Add one more step to the Base Question to make it more difficult and Create a new question.
# Changing the proper nouns, numerical values, fractions, multiples and problem background by getting inspiration from the Supplementary Question for generating a new question.
……
Base Question: <<given question A>>
Supplementary Question: <<given question B>>
……
二つの問題のうちはBase Questionとしてこの問題にone step追加する形でよりチャレンジングな問題を生成してもらいます。一方でSupplementary QuestionをGSM8Kのtrainデータセットからランダムに選択し、問題を新しく書き換えるための補助とします。予備実験としてプロンプトの変更を何度か試しましたが、複数回にわたる生成に対して多様な問題を生成するには、別のシード情報を入れる必要があると判断しました。高難易度化と補助問題による問題の書き換えを同時に行うことが重要で、片方ずつではCommon 7Bの生成方法よりも精度が落ちます。
この新しい生成手法で生成された問題とCommon 7B論文の手法で生成された問題を比較してみます。なお、補助問題を除いて両者のシード問題は同じです。
- GSM8Kからのシード問題
- Natalia sold clips to 48 of her friends in April, and then she sold half as many clips in May. How many clips did Natalia sell altogether in April and May?
- Common 7Bの手法で生成された問題例
- Ava sold bracelets to 60 of her classmates in June, and then she sold half as many bracelets in July. How many bracelets did Ava sell altogether in June and July?
- In June, Lily sold postcards to 60 of her classmates, and in July, she sold half as many postcards as she did in June. How many postcards did Lily sell altogether in June and July?
- In June, Ethan sold pencils to 36 of his classmates, and then he sold half as many pencils in July. How many pencils did Ethan sell altogether in June and July?
- 提案手法で生成された問題例
- Emma sold keychains to 40 of her classmates in March, and then she sold half as many in April. However, in May, she managed to sell twice the number of keychains she sold in April. How many keychains did Emma sell altogether in March, April, and May?
- Samantha sold handmade soaps to her customers. In February, she sold 60 soaps, and then she sold twice as many soaps in March. However, due to a shortage of ingredients, she could only sell half the number of soaps she sold in March in April. How many soaps did Samantha sell altogether in February, March, and April?
- Natalia sold bracelets to 36 of her classmates in June, and then she sold twice as many bracelets in July. However, 15% of the bracelets sold in July were returned due to defects. How many bracelets did Natalia sell altogether in June and July (after accounting for the defective returns)?
シード問題と比較すると、どちらの手法でも名詞や数値が変化している部分が見受けられます。しかし、Common 7Bの手法で生成された問題間では、数値や倍数(例えば「half」など)が同一であることが多いです。一方で、提案手法で生成された問題は、基本的な構造は似ていますが、数値、倍数、月などが問題ごとに異なっています。さらに、問題文が長くなり、解答に必要なステップ数が増えている問題も存在します。
定量的な評価のために、GSM8Kの訓練問題7473件をそれぞれシード問題(提案手法ではBase Question)とし、それぞれに対して10件の新しい問題を生成しました。その後、同一のシード問題から生成された問題間の類似度を平均化しました。その結果、Common 7Bでは平均類似度が0.8124であったのに対し、提案手法では0.6859となりました。これにより、補助問題を加えることで、同一のシード問題から生成されてもより多様な問題を生成できることが確認できました。
なお、類似度の計算には、Sentence Transformerを用いて合成問題の文章ベクトルを取得し、そのコサイン類似度を計算しました。
評価・考察
提案手法の評価を行います。学習の基本設定は先述の実験の概要と同様ですが、ここではカリキュラム学習も取り入れます。カリキュラム学習とは学習データを段階的に変えて学習していき、モデルの学習効率と性能の向上を目指す手法です。提案手法で生成された問題は、オリジナルのGSM8Kの問題よりも難易度が上がっているのでカリキュラムを組んで学習してみます。比較する学習カリキュラムは以下の5つです。
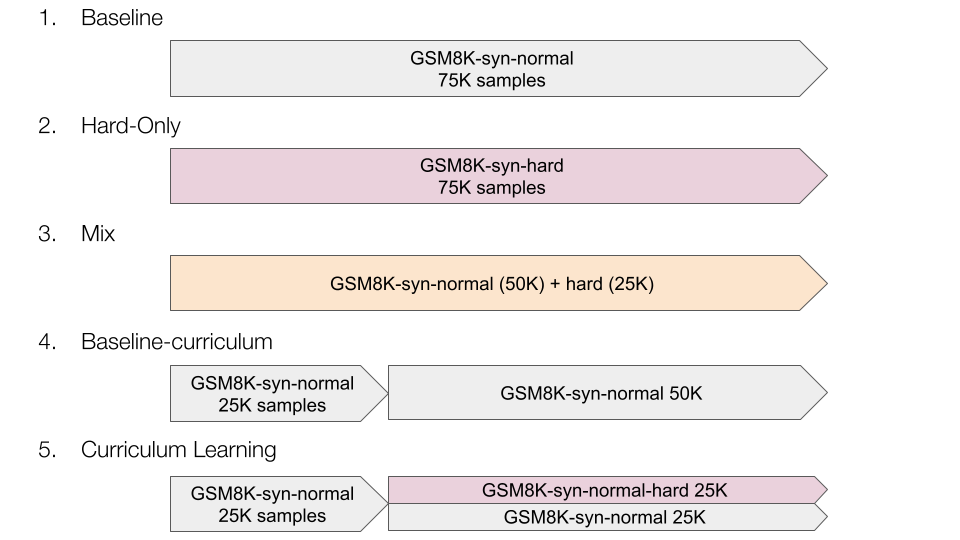
normalはCommon 7Bの手法で生成された問題で、hardが提案手法の問題です。
- Baseline : normal問題のみ
- hard-only : hard問題のみ
- Mix : normalとhard問題を2対1の割合で混合させたデータセット
- Baseline-curriculum : normal問題のみで学習を分けた場合(5との比較のため)
- Curriculam Learning : 最初にnormal問題で学習し、その後に1対1の割合でnormalとhard問題を混合したデータセットで学習
すべての学習結果を以下に示します。
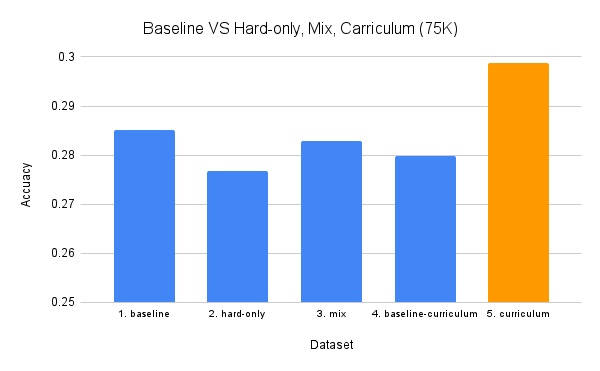
提案手法であるhard問題を単体やnormal問題と混合させるだけでは、精度の向上にはつながらないことが分かりました。しかし、適切にカリキュラム学習を行うことで、ベースラインを超えることが可能となります。念のため、カリキュラム4のnormal問題だけを分けて学習してみましたが、これはベースラインを下回りました。これにより、データセット自体の効果が確認できました。また、高難易度化と補助問題による多様化をそれぞれ単独で行った場合、ベースラインよりも正答率が約1%ほど低下することが分かりました。したがって、これらの手法は同時に行うことが重要であると言えます。理由としては、高難易度化を行う際に補助問題を追加しないと、モデルが「One step追加する」という指示に重きを置きすぎ、元の問題から変えた問題の生成がおろそかになる可能性があると考えられます。
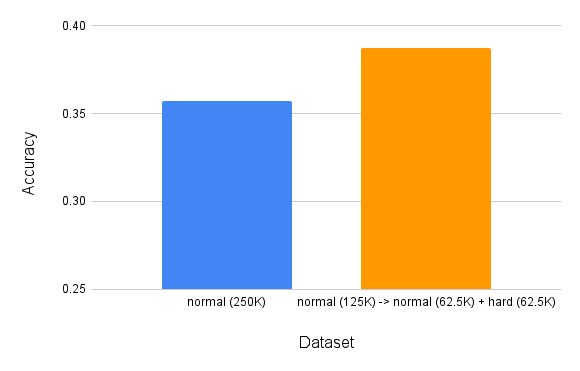
さらに、総学習サンプル数を250Kまで増加させ、カリキュラム学習(データの割合はグラフに記載)を適用した結果、正答率は35.71%から38.74%へと約3%向上しました。ファインチューニングを行わなかった場合、GSM8Kのテスト問題を5%しか解けなかったPLaMo-1Bですが、データセットの合成とカリキュラム学習を行うことで、約40%の問題を解くことが可能となりました。
test問題を解答step数ごとに分けて正答率を算出すると次のようになります。
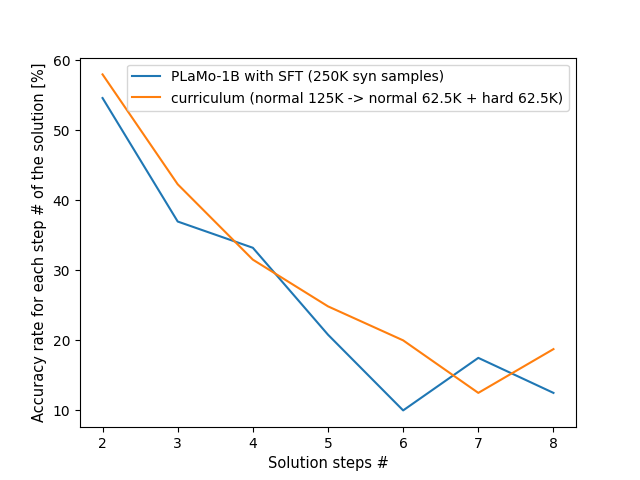
依然としてステップ数の多い問題の正答率の低さは課題ですが、解答ステップ数6の問題は元より約2倍に改善しています。これはステップ数の多い問題で学習した効果だと考えられます。その他、ステップ数の少ない問題でも一定割合ずつ改善していることが分かります。
また、提案手法で生成したhard問題をシード問題として再度生成すると合成問題のバリエーションを無数に増やすことができます。最初の合成問題を第1世代とすると、第2世代以降を生成できることになります。カリキュラム4において、第1世代のhard問題の代わりに第2世代の問題を利用した場合の結果を次に示します。
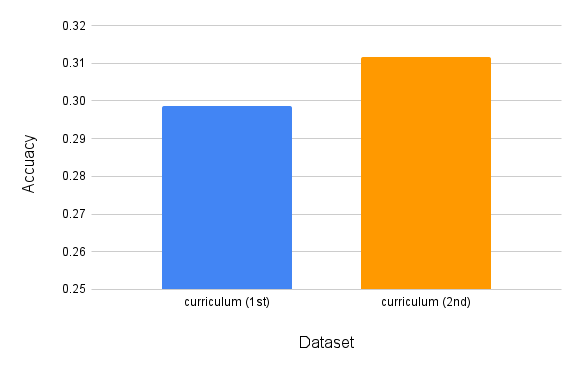
総学習サンプル数が75Kの場合、第1世代の問題よりも第2世代の問題でカリキュラム学習を行うと、正答率がさらに1.3%向上しました。他の実験結果と照らし合わせると、学習サンプル数を増やした場合に必ずしも第2世代の問題の方が優れているわけではありませんでしたが、第2世代以降の問題もカリキュラム学習により効果的に活用できる可能性が確認できました。
解答過程生成時の自己修正「self-correct」
ここまでが上手くいった例ですが、思うような結果が出なかった実験も多数ありました。そのうちの1つを簡単に紹介します。
解答はstep-by-stepで行っていますが、問題文の理解不足により、途中stepのどこかで事実に基づかない情報を生成する「hallucination」を起こすことがあります。例えば以下のようなSFT済みのPLaMo-1Bによる誤答があります。
Test Question:
A classroom has a whiteboard which is shared between the 4 teachers who take turns using the classroom. Each teacher has 2 lessons per day and uses the whiteboard in each lesson. If the whiteboard is cleaned 3 times per lesson, how many times is the whiteboard cleaned in a day?Answer by PLaMo-1B with SFT:
To find out how many times the whiteboard is cleaned in a day, we first need to determine how many lessons are taken by all teachers in a day. Since there are 4 teachers and each teacher takes 2 lessons per day, the total number of lessons taken in a day is:
4 teachers * 2 lessons/teacher = 8 lessons/day
Next, we know that each lesson lasts for 1.5 hours. Therefore, the total time taken for all lessons in a day is:
8 lessons/day * 1.5 hours/lesson = 12 hours/day
Now, we know that the whiteboard is cleaned 3 times per lesson. So, the total number of times the whiteboard is cleaned in a day is:
12 hours/day * 3 cleanings/hour = 36 cleanings/day
Therefore, the whiteboard is cleaned a total of 36 times in a day.
#### 36
要約すると、「1日に授業を2回ずつ行う4人の先生がいます。1授業で3回ホワイトボードを掃除するとなると1日合計何回掃除することになるか」という問題です。1日あたりの授業数が4×2=8回で、合計掃除回数は8×3=24回と求まります。しかし、LLMは1授業は1.5時間という問題文にない情報を突如出力し、結果的に以降の計算が合いません。このような問題文にはない情報を追加してしまうケースがあります。また、必要な計算stepを飛ばしてしまったり、逆に既に行った計算を繰り返すこともあります。
これらの誤った解答過程を推論中にLLM自身に認識させ、自己修正させることを考えます。先行研究として「Physics of Language Models: Part 2.2, How to Learn From Mistakes on Grade-School Math Problems」[11] を簡単に紹介します(以降はPhysics LMと呼びます)。Physics LMではGSM8Kから算術の難しさや常識知識を除去した新しいiGSMデータセットを使用し、各問題はパラメータの依存グラフを持っています。パラメータの依存については、数学の問題を解くときにパラメータBを求めるにはパラメータAを先に求める必要がある場合、パラメータBはAに依存しているといえます。さて、このデータセットの解答ステップにあえて次の2種類のエラー文を加えます。
1. retry_weak : 解答の後方の文をランダムに選択し、パラメータを[BACK]スペシャルトークンで置換し前方に挿入
2. retry_miss : 問題文から未出のパラメーターをランダムに選び、1同様に[BACK]スペシャルトークンで置換し挿入
上記のエラー文を加えた解答例を示します。
問題:
The number of each Riverview High’s Film Studio equals 5 times as much as the sum of each Film Studio’s Backpack and each Dance Studio’s School Daypack. The number of each Film Studio’s School Daypack equals 12 more than the sum of each Film Studio’s Messenger Backpack and each Central High’s Film Studio. The number of each Central High’s Film Studio equals the sum of each Dance Studio’s School Daypack and each Film Studio’s Messenger Backpack. The number of each Riverview High’s Dance Studio equals the sum of each Film Studio’s Backpack, each Film Studio’s Messenger Backpack, each Film Studio’s School Daypack and each Central High’s Backpack. The number of each Dance Studio’s School Daypack equals 17. The number of each Film Studio’s Messenger Backpack equals 13. How many Backpack does Central High have?エラー文を含む解答:
Define Dance Studio’s School Daypack as p; so p = 17.
Define Film Studio’s School Daypack as [BACK].
Define Film Studio’s Messenger Backpack as W; so W = 13.
Define Central High’s Classroom as [BACK].
Define Central High’s Backpack as [BACK].
Define Central High’s Film Studio as B; so B = p + W = 17 + 13 = 7.
Define Film Studio’s School Daypack as g; R = W + B = 13 + 7 = 20; so g = 12 + R = 12 + 20 = 9.
Define Riverview High’s Dance Studio as [BACK].
Define Film Studio’s Backpack as w; so w = g + W = 9 + 13 = 22.
Define Riverview High’s Dance Studio as [BACK].
Define Central High’s Backpack as c; so c = B * w = 7 * 22 = 16.
エラー文1はあえて未だ計算できないパラメータを先に解答に挿入することで、[back]トークンを使うことで解答順序のミスを学習させます。エラー文2は解答に使わないパラメータを挿入することで誤ったステップを認識させます。論文では特にretry_weak形式のデータで事前学習することで精度が向上したと記しています。mまたLoRAでの事後学習ではなく、事前学習から行う必要があることも述べています。この論文の成果を利用することを考えます。
本研究では、GSM8Kの問題をもとにLLMで問題と解答を生成しているため、完全にパラメータの依存関係を考慮した形式的なデータセットではありません。そこでretry_weak, retry_missの手法をより簡略化し、最初と最後以外の解答ステップの1文をランダムにコピーし、元の位置より前方のランダムな位置に挿入します。このときにコピーした文の最初に出てくる数値、数値がない場合はランダムな位置の単語を[back]で置換し、以降の単語を削除します。最初の数値とするのは、間違った計算をさせる前にLLMに間違いを認識してもらうためです。また、ランダムに他の問題の解答過程から1文を取ってきて同様に挿入します。最終的に全データセットの半分の解答にエラー文を1つ入れることにします。補足としてここで使う[back]はスペシャルトークンではなく文字列です。以下にエラー文を入れた解答例を示します。
To find out how many more books Sarah donated than Tim, we first need to calculate the total number of books each of them donated.
Tim donated:
3 boxes * 18 books/box = 54 books
Sarah donated:
So, Sarah donated [back]
4 boxes * 15 books/box = 60 books
Now, we subtract the number of books Tim donated from the number of books Sarah donated to find the difference:
60 books (Sarah’s donation) – 54 books (Tim’s donation) = 6 books
So, Sarah donated 6 more books than Tim.
#### 6
上記の例はすべての計算が終わる前に結論を出力しようとするのを、[back]で自己修正させているといえます。
この新しいデータセットで学習した結果を表に示します。事前学習は厳しいので、フルパラメータのファインチューニングを行います。
| 条件 | GSM8K test setのAccuracy |
| PLaMo-1B エラー文ありの250Kサンプルで学習 | 0.3578 |
| PLaMo-1B エラー文なしの250Kサンプルで学習 | 0.3571 |
表の結果より、エラー文を入れても精度の改善は見られませんでした。実際のtestセットの解答生成結果を見ると、1319件中37件の問題しか[back]が出現していませんでした。また、出現していても適切な使われ方がされているとはいえず、エラー文を入れないで学習したときと正誤に変化はありませんでした。さらにエラー文の挿入位置の制限をなくしたり、[back]の挿入位置を文末にそろえたり、何度か条件を変えてもいい結果は得られませんでした。原因としては次のことが考えられます。
- 解答内に多くても1つしかエラー文がなく[back]を学習できなかった
- 学習データ量が少なかった
- LoRAチューニングだけでなく、フルパラメータのファンチューニングでも効果が得られない可能性
- [back]がスペシャルトークンではなかった
- LLMが生成した解答の形式は多様で、[back]を学習しづらかった
少し考えただけでも原因は無数に出てくるので、インターン期間中に解決することはかないませんでしたが、生成の自己修正は面白い手法なので別の機会にもう一度チャレンジしたいです。
その他の工夫
その他インターン期間中に試した数学データセット作成手法を記します。詳細な結果は割愛します。
SCoT : Strategic Chain-of-Thought [12]
解答をstep-by-stepで生成する前に解答のための戦略を考えさせるアプローチです。プロンプトの詳細は元論文へ。SCoTで解答を生成させると、問題の条件を確認しながら簡潔に推論していくことが分かります。7.4Kサンプルの学習では若干の改善が見られましたが、学習サンプル数を増やすとCommon 7Bと比較して伸び悩みました。根拠に基づいていない私の予想ですが、プロンプトでの指示を増やしたことで解答の多様性が失われたことが原因だと思いました。解答方法の多様性が重要であることは先行研究で述べられています。(参考)
四則演算を先に学習
思い付きで試した方法です。私たちが算数を学ぶときに先に基礎計算をしてから、文章題に入ります。そこで、3桁までの整数の四則演算問題と途中式を含んだ解答を構文木を使って生成します。この四則演算データセットを先に学習してからGSM8Kの合成問題に入るカリキュラムを組みました。しかし、結果の改善は見られませんでした。LLMは文章問題をCoTで解くときに自然言語を頼りに問題を分解していることが多く、実際には複雑な入れ子式の演算を直接解くというより、簡単な演算を繰り返しています。よって、GSM8Kでは計算部分のみを学習するメリットが少なかったのだと考えられます。
別のデータセットを用いる
GSM8Kより少し難しいAQUA-RATデータセットの問題をカリキュラム学習に組み込みました。AQUA-RATは選択式問題なので、一部の問題をフィルタリングしてからルールベースで数値回答形式に変換しました。中高生レベルの問題なので座標幾何などGSM8Kとは内容が異なるものも多く含まれていたためか、GSM8Kでの改善は見られませんでした。しかし、MATHCODER [13] で提案されているGSM8KとMATHの間の難易度の問題を生成するinterpolationは、適切にカリキュラム学習すると提案手法に匹敵するほど有効であることが分かりました。
問題の修正データセットを用いる
Common 7Bの方法では問題を生成すると同時に、問題が適切に解けるかどうか確認し修正を行っています。そこで、この問題生成の副産物である問題修正情報を使います。この修正データは問題を分析している文章であり、生成問題の後ろに結合してSFT前の追加学習に用いました。結果の改善はありませんでしたが、方法によっては有効活用できる可能性のあるデータと考えています。
Self feedback
7.4Kサンプルの合成問題で学習してから、オリジナルのtrainデータセットで評価します。次に間違ったオリジナル問題をシードとする合成問題のみで再度ファインチューニングします。この合成問題のフィルタリングは問題の多様性を低下させるだけで上手くいきませんでした。
FOBAR
合成された問題文中の数値のうち一つをxとし、最終解答を問題文の最後に与えたうえで、xを解答させる問題の作り替え手法です。これはMetaMathでも使用されているFOBAR [14] という手法です。合成問題とこのFOBAR問題を混合して学習に用いましたが、大きな改善は確認できませんでした。学習データ量を増やすとどうなるかが気になります。
無駄な文の挿入
問題文に無駄な1文を挿入するというシンプルな方法です。この文は問題文に何かしらの関係があり、数値も含んでいるが解答には用いないものでMixtralに生成してもらいます。問題文に無駄な文があることで解答の際により高い問題理解能力が求められます。無駄な文を挿入した問題を含むデータセットで学習しましたが、結果の向上はありませんでした。この方法も原因の解明のためにさらなる実験が必要です。
まとめ
PLaMo-1Bという比較的小さなLLMでも大規模な数学の合成問題によるSFTは有効であることが分かりました。また、提案手法によって先行手法であるCommon 7Bでの結果を上回ることができました。多くの実験を行いましたが、最終的にGSM8Kのスコアを上げるには、GSM8Kのオリジナル問題から離れすぎない程度に高難易度で多様な合成問題が必要であることが分かりました。
しかし、GSM8K以外のデータセットでは評価ができなかったため、他の数学推論タスクでの提案手法の有効性を調べる必要があります。
感想
7週間という長期インターンシップでしたが、3連休や中間・最終発表の予定が挟まるなど、時間があっという間に過ぎてしまった感じがします。インターンシップが始まる前から、メンターの方から「7週間は意外と短い」と言われていたので、「思い立ったらすぐに試す」という姿勢を一貫して保つことを心掛けました。
数学推論タスクを本格的に扱うのは初めてだったため、まずはリサーチを一定程度行い、再現実験を通じてLLMにおける数学推論の難しさを学びました。その後も、さまざまな改善手法を試し、多くの失敗を経験することで、LLMの推論能力や合成データセットに対する理解が深まったと感じています。
最終的には、最後に行った実験で良い結果が得られたため、多くの実験を行ったことが有益だったと思います。おそらく50回以上、様々な手段を試しながらLLMの学習を繰り返しました。もっと時間があったら、これを試してあれも試してとやりたいことは尽きませんが、手厚いサポートと潤沢な計算資源のおかげで、限られた時間の中でなるべく多くのことができたと思います。
また、フルタイムの社員の方と一緒にボードゲームを楽しんだり、読書会に参加したりと、社内の交流やイベントは非常に活発でした。歓迎会や送別会を含め、企画を手掛けてくださった方々には心から感謝しています。
最後に、日々的確なアドバイスをくださったメンターの皆様、LLMチームの皆様、計算環境を整備してくださった皆様、本当にお世話になりました。深く感謝申し上げます。
メンターより
PFN/PFEではこのようなLLM性能改善のための研究開発を進めています。本取り組みで得られた知見・成果は今後PLaMoに取り入れていく予定です。
付録
問題生成プロンプト
提案手法の問題生成プロンプトです。<<given question A>>と<<given question B>>にベース問題と補助問題を入力します。
Please act as a professional math teacher.
Your goal is to create high quality math word problems to help students learn math.
You will be given two math questions, Base Question and Supplementary Question. Please create a new and more challenging question based on the given Questions and following instructions.
To achieve the goal, you have four jobs.
# Add one more step to the Base Question to make it more difficult and Create a new question.
# Changing the proper nouns, numerical values, fractions, multiples and problem background by getting inspiration from the Supplementary Question for generating a new question.
# Check the question by solving it step-by-step to find out if it adheres to all principles.
# Modify the created question according to your checking comment to ensure it is of high quality.
You have six principles to do this.
# Please generate only one problem. For example, DO NOT ask, ‘how many of A are there, and how much does it cost?’.
# Ensure the new question only asks for one thing, be reasonable, be based on the Given Question, and can be answered with only a number (float or integer). For example, DO NOT ask, ‘what is the amount of A, B and C?’.
# Ensure the new question is in line with common sense of life. For example, the amount someone has or pays must be a positive number, and the number of people must be an integer.
# Ensure your student can answer the new question without the given question. If you want to use some numbers, conditions or background in the given question, please restate them to ensure no information is omitted in your new question.
# Please DO NOT include solution in your question.
# If the created question already follows these principles upon your verification. Just keep it without any modification.
Base Question: <<given question A>>
Supplementary Question: <<given question B>>
Your output should be in the following format:
CREATED QUESTION: <your created question>
VERIFICATION AND MODIFICATION: <solve the question step-by-step and modify it to follow all principles>
FINAL CREATED QUESTION: <your final created question>
合成データセットの大規模化効果の数値結果
lm-evaluation-harnessで各モデルにおけるGSM8KタスクのStrict-match Accuracyを評価したものです。「syn」は合成データでのSFTを、「ori」はオリジナルデータでのSFTを示しています。基本的には記載の学習サンプル数を3 epoch回していますが、10 epochと記載の結果は例外です。
| gsm8k | strict match |
| phi-1.5 | 0.3192 |
| LLaMA2-7B | 0.1531 |
| PLaMo-1B | 0.0493 |
| PLaMo-1B-ori-7.4k-5shots | 0.1554 |
| PLaMo-1B-ori-7.4k-5shots-10epoch | 0.0970 |
| PLaMo-1B-syn-7.4k-5shots | 0.1433 |
| PLaMo-1B-syn-25k-5shots | 0.2077 |
| PLaMo-1B-syn-75k-5shots | 0.2851 |
| PLaMo-1B-syn-125k-5shots | 0.2904 |
| PLaMo-1B-syn-250k-5shots | 0.3571 |
参考文献
[1] Cobbe, K., Kosaraju, V., Bavarian, M., Chen, M., Jun, H., Kaiser, L., … & Schulman, J. (2021). Training verifiers to solve math word problems. arXiv preprint arXiv:2110.14168.
[2] Ling, W., Yogatama, D., Dyer, C., & Blunsom, P. (2017). Program induction by rationale generation: Learning to solve and explain algebraic word problems. arXiv preprint arXiv:1705.04146.
[3] Hendrycks, D., Burns, C., Kadavath, S., Arora, A., Basart, S., Tang, E., … & Steinhardt, J. (2021). Measuring mathematical problem solving with the math dataset. arXiv preprint arXiv:2103.03874.
[4] Wei, J., Wang, X., Schuurmans, D., Bosma, M., Xia, F., Chi, E., … & Zhou, D. (2022). Chain-of-thought prompting elicits reasoning in large language models. Advances in neural information processing systems, 35, 24824-24837.
[5] Li, C., Wang, W., Hu, J., Wei, Y., Zheng, N., Hu, H., … & Peng, H. (2024). Common 7b language models already possess strong math capabilities. arXiv preprint arXiv:2403.04706.
[6] Touvron, H., Martin, L., Stone, K., Albert, P., Almahairi, A., Babaei, Y., … & Scialom, T. (2023). Llama 2: Open foundation and fine-tuned chat models. arXiv preprint arXiv:2307.09288.
[7] Gao, L., Tow, J., Abbasi, B., Biderman, S., Black, S., DiPofi, A., … Zou, A. (12 2023). A framework for few-shot language model evaluation (Version v0.4.0). Version v0.4.0. doi:10.5281/zenodo.10256836
[8] Hu, E. J., Shen, Y., Wallis, P., Allen-Zhu, Z., Li, Y., Wang, S., … & Chen, W. (2021). Lora: Low-rank adaptation of large language models. arXiv preprint arXiv:2106.09685.
[9] Li, Q., Cui, L., Zhao, X., Kong, L., & Bi, W. (2024). GSM-Plus: A Comprehensive Benchmark for Evaluating the Robustness of LLMs as Mathematical Problem Solvers. arXiv preprint arXiv:2402.19255.
[10] Yu, L., Jiang, W., Shi, H., Yu, J., Liu, Z., Zhang, Y., … & Liu, W. (2023). Metamath: Bootstrap your own mathematical questions for large language models. arXiv preprint arXiv:2309.12284.
[11] Ye, T., Xu, Z., Li, Y., & Allen-Zhu, Z. (2024). Physics of Language Models: Part 2.2, How to Learn From Mistakes on Grade-School Math Problems.
[12] Wang, Y., Zhao, S., Wang, Z., Huang, H., Fan, M., Zhang, Y., … & Liu, T. (2024). Strategic Chain-of-Thought: Guiding Accurate Reasoning in LLMs through Strategy Elicitation. arXiv preprint arXiv:2409.03271.
[13] Wang, K., Ren, H., Zhou, A., Lu, Z., Luo, S., Shi, W., … & Li, H. (2023). Mathcoder: Seamless code integration in llms for enhanced mathematical reasoning. arXiv preprint arXiv:2310.03731.
[14] Jiang, W., Shi, H., Yu, L., Liu, Z., Zhang, Y., Li, Z., & Kwok, J. T. (2023). Backward reasoning in large language models for verification. arXiv preprint arXiv:2308.07758.