Blog
深層学習の計算は、テンソルと呼ばれる多次元配列で記述されています。MN-Core では、ツリー状の通信路で繋がった大量の演算器が並列に動作しますが、配列に対する計算をツリー状に並んだ演算器にどう割り当てると効率的かというのは自明な問題ではありません。この記事では、この問題を記述するために MN-Core コンパイラチームが用いている TensorLayout という記法を紹介します。
※本稿では密な行列を扱います。疎行列の表現は扱いません。
CPU/GPU におけるメモリ配置
MN-Core について考える前に、まずは CPU や GPU の DRAM 上でどのように配列が配置されているかを紹介します。NumPy や CuPy、PyTorch では、strided layout という方法で要素がメモリ上に配置されています(定まった名称がないのですが、名前があった方が話がしやすいので本稿ではこう呼ぶことにします)。これは、shape と strides という二つの整数値タプルの組でレイアウトを表現する手法です。
簡単な例から紹介します。2×3 の行列は、たとえば PyTorch において
a = torch.zeros((2, 3))
などのように作ることができます。このとき、デフォルトでは row major と呼ばれる順序でメモリ上に要素が配置されます。これは、2 * 3 = 6 要素分の連続領域に図 1 の順序で要素を配置するものです。

図 1: 2×3 行列の要素を row major フォーマットでメモリに配置する
さて、strided layout においては、行列のこのようなメモリ配置を shape=(2, 3), strides=(3, 1) のように表現します(注: ここでは strides は要素を単位として書いています。NumPy/CuPy の場合、strides は byte を単位とし、たとえば float32 の配列なら strides=(12, 4) のように 4 倍の整数が使われます)。このうち、shape は NumPy や PyTorch を使ったことがあれば馴染みがあると思いますが、strides は初めて見る方もいるかもしれません。これは、添字 i, j と要素 a[i, j] のメモリ上の位置との関係を表していて、次のように読みます。
- i が 1 だけ増えたら、メモリ上の位置は 3 要素分だけ増える
- j が 1 だけ増えたら、メモリ上の位置は 1 要素分だけ増える(つまり、メモリ上ですぐ隣)
たとえば図 2 のように、a[1, 1] という要素は、a[1, 0] という要素の隣にあります。これは、2つ目の添字だけが 1 異なっていて、2つ目の添字の stride が 1 であることからわかります。一方、a[1, 0] という要素は、a[0, 0] という要素と 3 つ分だけ離れた位置にあります。これは、1つ目の添字だけが 1 異なっていて、その stride が 3 であることからわかります。これらを組み合わせて、a[1, 1] という要素が a[0, 0] から 4 要素分離れていることもわかります。
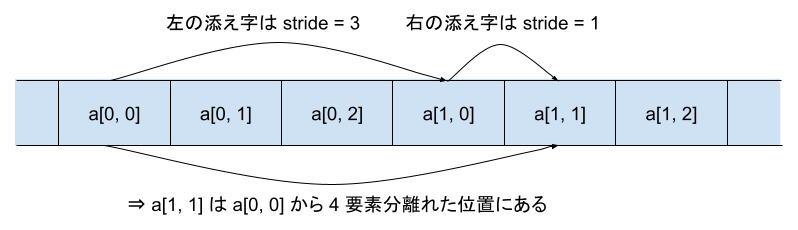
図 2: メモリ上での行列要素のアドレスは、添字の差と stride から計算できる
この strided layout という表現には、いくつかの利点があります。
- 転置 (numpy.transpose, torch.permute) 操作が要素をコピーせずに実現できます。たとえば、上の 2×3 行列 a を転置して 3×2 行列を得るには、メモリ上の要素は動かさずに shape と strides だけ並び替えて shape=(3, 2), strides=(1, 3) とすれば完了します。
- スライス操作がゼロコピーで実現できます。たとえば、同じ行列 a の左 2 列だけ取り出す操作 a[:, :2] は、strides をいじらずに shape だけ (2, 2) に変更することで実現できます。また、a の列を真ん中だけ飛ばして取り出す操作 a[:, ::2] は、shape を (2, 2) とした上で、strides を右の軸についてだけ 2 倍して (3, 2) とすることで実現できます。
一方、注意点として Reshape 操作(要素を row major に並べたときの順序を変えずに shape だけ変更する)が必ずしもゼロコピーでなくなるという性質があります。たとえば、転置した状態で行列をベクトルに展開する a.transpose(1, 0).reshape(6) などのコードは、実際にメモリ上で順序を並び替える必要があります。
あとあとの準備として、この strided layout に対する記法を導入しておきます。shape=(A, B), strides=(a, b) のようなレイアウトを (A:a, B:b) のように書くことにします。コロン : の左に要素数、右に stride を書いたものを行、列とカンマ区切りで書いています。例えばここで扱った shape=(2, 3), strides=(3, 1) というレイアウトであれば (2:3, 3:1) となります。多次元配列では添字が 3 つ以上あるようなものを扱うこともありますが、その場合はさらにカンマで繋げて書きます。
MN-Core のツリー構造
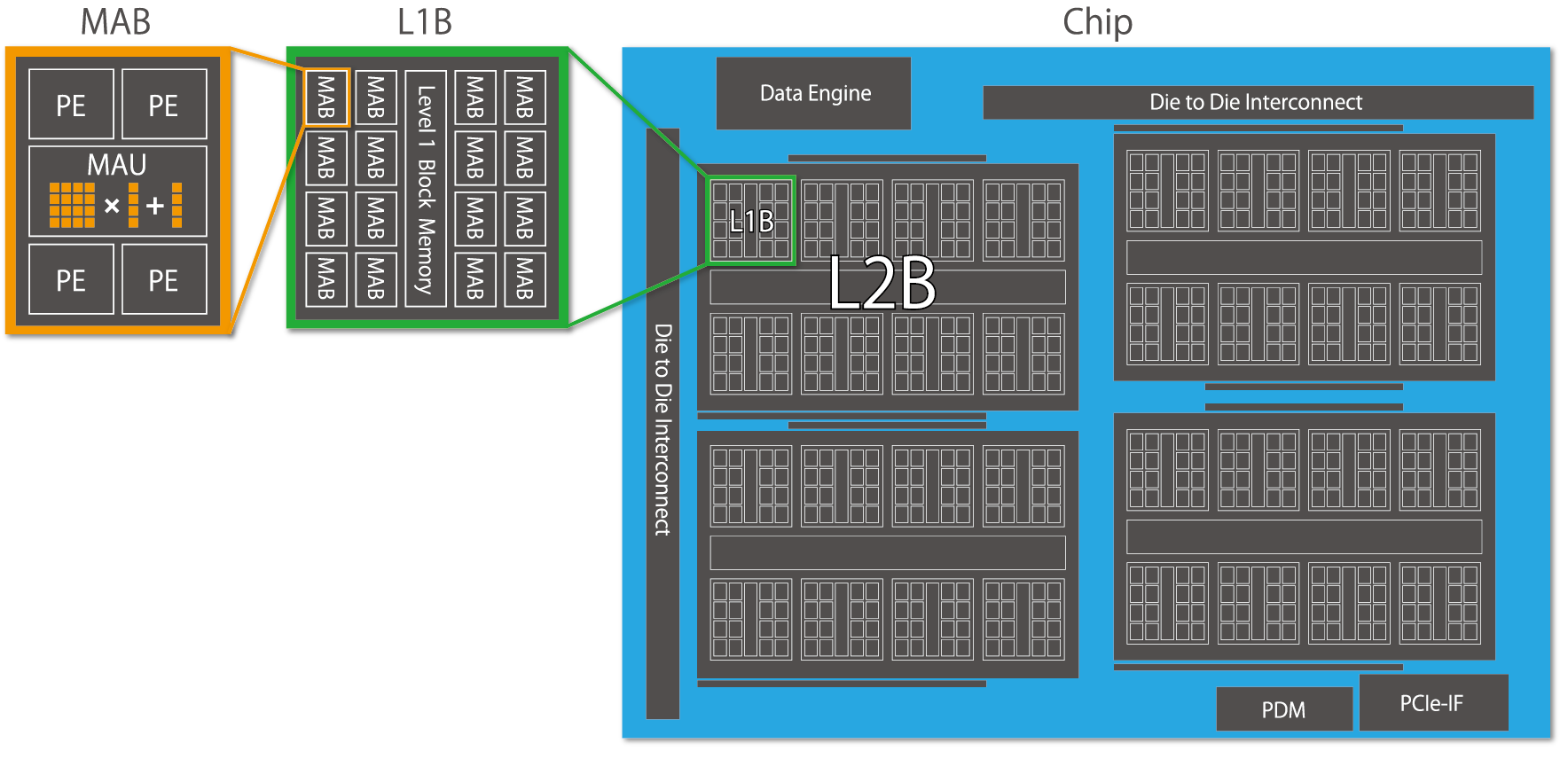
図 3: MN-Core のツリー構造
PFN で開発している MN-Core というプロセッサは、図 3 のような階層的な構造を持っています。この階層構造を持ったチップが 4 枚並んで一つのボードを構成しています。この図に従うと、
- ボードは 16 個の L2B からなり、
- 各 L2B は 8 個の L1B からなり、
- 各 L1B は 16 個の MAB からなり、
- 各 MAB は 4 個の PE からなる
というツリー構造が得られます。それぞれの PE は高速にアクセスできるローカルメモリ (LM) を持っています。
さて、MN-Core は演算性能を重視しています。ボード上には大容量の DRAM がありますが、一つの演算のたびに DRAM を読み書きするのでは演算器が遊んでしまいます。そのため、できるだけ演算の入出力は LM で完結させることが重要になります。ここで問題となるのが、多次元配列のメモリレイアウトです。一次元のアドレス空間を持つ DRAM 上では、strided layout を用いることで効率的に要素の配置を表現していました。一方、MN-Core の LM は一次元のアドレス空間がなく、ツリー状に散らばったメモリがそれぞれアドレス空間を持っているため、strided layout をそのまま使えません。ツリー状に分散した LM に多次元配列を展開するためには、新しいレイアウトの記法が必要です。それが TensorLayout です。
階層が一つの場合のレイアウト
まずは話を簡単にするために、4 つの PE だけからなる仮想的なチップを考えましょう。LM はそれぞれの PE に付属し、全部で 4 つに分かれています。今、これらの LM に 12×8 の行列を展開するとします。TensorLayout では、行列を 4 つに分けるために、仮想的に長さ 4 の軸ができるようにこれを Reshape して、4 つの PE に分配する軸をアノテーションするという形で表現します。たとえば、図 4 のように、行で区切るレイアウトを考えます。
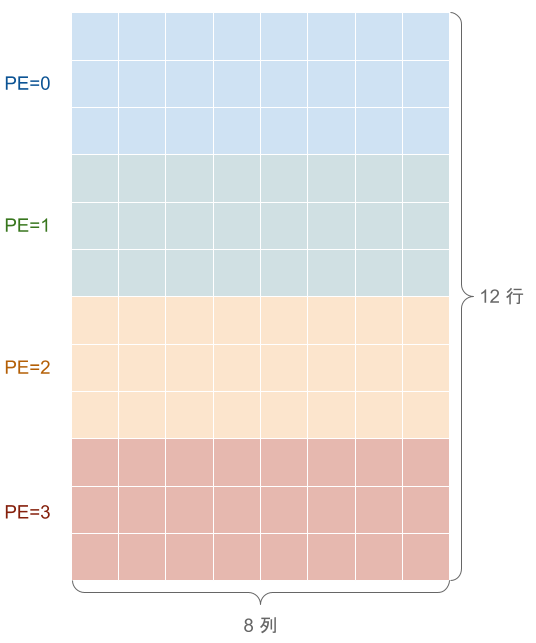
図4: 12×8 行列を 3 行ずつ 4 つの PE に分配する
このレイアウトは、12 個の行を 12=4×3 と分解して、”4×” の方向を PE で分割することに対応します。このことを、TensorLayout では ((4_PE, 3), (8)) のように書きます。ここで、タプルが入れ子になっていますが、外側のタプルは元の行列の形状 (12, 8) に対応しており、内側のタプルはそれぞれの軸をどのように Reshape するかを記述しています。_PE のように数字に接尾辞をつけることで、どの軸を 4 つの PE に分配するかを指示しています。
さて、((4_PE, 3), (8)) という表現は、LM 内のアドレスをどのように使うか指示しておらず、不完全です。接尾辞のない 3, 8 という軸は LM 内での配置を表しているので、これに strided layout に習って stride を設定します。ここでは 8 の軸が内側になる(=連続するアドレスが割り当てられる)ようにすることにします。そのようなレイアウトは、strided layout で導入した記法を使うと ((4_PE, 3:8), (8:1)) と書けます。これで 4 つの PE からなる小さなチップへ 12×8 行列を配置する方法が表現できました。
この記法では、他にもさまざまなメモリ配置を表現できます。たとえば、行ではなく列を分配するには、((12:2), (4_PE, 2:1)) とすれば良いです。
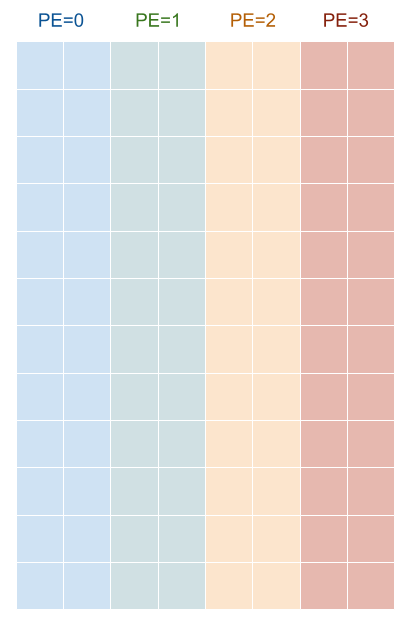
図5: レイアウト ((12:2), (4_PE, 2:1)) の可視化
また、3 行ずつにまとめるのではなくて、連続する 4 行を別々の PE に分配したい場合は、((3:8, 4_PE), (8:1)) と表現できます(実は、MN-Core では PE に関しては命令の都合でこのように内側で分割するのが一般的です)。
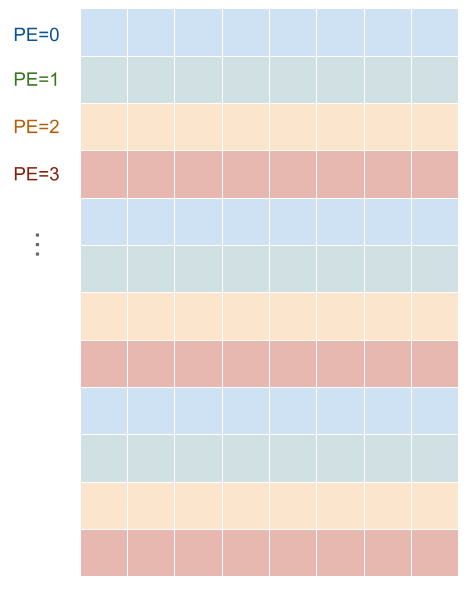
図6: レイアウト ((3:8, 4_PE), (8:1)) の可視化
もう一つのパターンとして、行と列をどちらも 2 分割して、全体として 4 分割することも考えられます。たとえば、次の図のように 12×8 の行列を 6×4 のブロックに分けて、この 4 つのブロックをそれぞれ別々の PE に分配することを考えます。

図7: 12×8 行列を 4 つの 6×4 ブロックに分割する
この場合、((2_PE, 6:4), (2_PE, 4:1)) と書けると良さそうです。この表現には、二つの “2_PE” という軸をどう解釈するかという問題があります。4 つの PE に 0, 1, 2, 3 と番号がついているとして、次の図のように二つのパターンがあります。
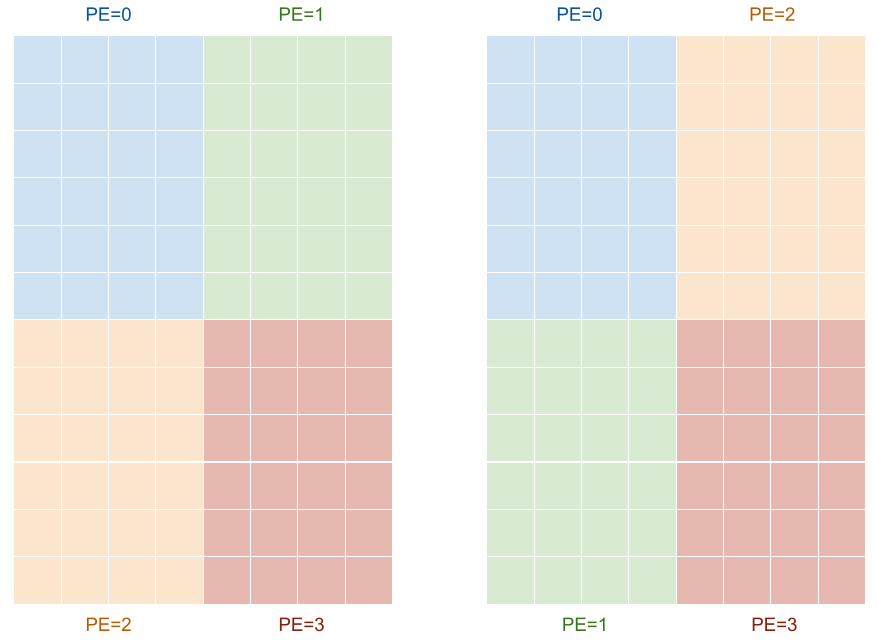
図8: 4 PE を 2×2 に分ける方法は 2 通りある。
これは、つまり二つの “2_PE” 軸に関して、その添字が 1 進んだときに PE の番号を 1 だけ進めるか 2 進めるかの組み合わせが二通りあるということです。これは、strided layout で扱ったのと同じ問題ですので、stride を指定することで解決します。
- 図 8 左のように配置する場合、((2_PE:2, 6:4), (2_PE:1, 4:1)) と書きます。
- 図 8 右のように配置する場合、((2_PE:1, 6:4), (2_PE:2, 4:1)) と書きます。
別の言い方をすれば、4 つの PE の番号もある種のアドレス空間だと思って strided layout を適用するということです。TensorLayout は、複数のアドレス空間を組み合わせる場合の strided layout の一般化になっています。
ここまでくると記法がややこしいので、PE が一箇所にしか現れないレイアウトの場合には、stride は今まで通り省略することにします。
パディングの扱い
さて、行列の行や列の数は、必ずしも 2 や 4 の倍数とは限りません。MN-Core は、SIMD 演算を行うことから、PE ごとに異なる要素数の配列を処理するのには向きません。そこで、半端なサイズの行列は綺麗なサイズになるまでパディングします。たとえば、10×7 の行列を LM に展開したい場合、これを 12×7 にパディングすれば ((3:7, 4_PE), (7:1)) というレイアウトで配置できます。このようにパディングまで含めたレイアウトは、パディング前の形状を前置して (10,7)/((3:7, 4_PE), (7:1)) のように書きます。この記法は特に PadLayout と呼んでいます。同じ行列を列について PE に分配したい場合、10×8 にパディングした (10,7)/((10:2), (2:1, 4_PE)) というレイアウトが使えます。このように、必要なパディングの位置と量はレイアウトによって変わります。
レイアウトの broadcast
場合によっては、行列を 4 つの PE で分割せずに、同じ行列を全ての LM にコピーしてばら撒きたいこともあります。TensorLayout は、単に “_PE” の軸を使わないことでこれを表現します。つまり、((12:8), (8:1)) と書いたら、これは 4 つの PE それぞれの LM に行列全体のコピーを配置するということになります。これは broadcast と呼ばれます。PE について broadcast されていることを明示したいときには、((12:8), (8:1); B@[PE]) と書くこともあります。
複数の階層を使ったレイアウト
ここまで、PE が 4 つあるだけの小さなアーキテクチャにおけるレイアウトを考えました。実際の MN-Core には、上で見た通り 16 個の L2B と、8 個の L1B と、16 個の MAB があります。そこで、これらを別々の軸に割り当てることで、大きな行列やテンソルを MN-Core 上の全ての LM に分配します。読み方は PE のみを扱ったこれまでの例と同じです。
具体例を見てみましょう。今度は大きな行列 1024 x 512 を考えます。これを
- 1024 行を 8 行のまとまりごとに 8 つの L1B に、さらにそれでできた 64 行のまとまりごとに 16 個の L2B に分配し、
- 512 列について、連続する 4 列は 4 つの PE に分配した上で、32 列のまとまりごとに 16 個の MAB に分配する
というレイアウトで配置しようと思います。これは、((16_L2B, 8_L1B, 8:8), (16_MAB, 8:1, 4_PE)) と表現できます。
以上が、MN-Core コンパイラで利用しているレイアウト記法の考え方です。長くなってしまったので今回のブログでは最終的な全階層を用いたレイアウトは少し触れるのみとなりましたが、この記法は表現力が非常に高く、込み入った例でも可読かつコンピュータが処理可能な形で表現できます。また、データや処理を重複しないように並列処理する用途であれば、MN-Core の構造以外にも応用できることがわかってきています(論理的に並列に扱えれば良いというのも面白い点です。たとえば、コンパイラ内では同じ記法を用いて、ループのように処理を時間方向に分割して計算することを “_Time” という軸で表現しています)。
MN-Core コンパイラには、計算グラフ中の全ノードの入出力に適切な TensorLayout を割り当てる layout plan という処理があります。レイアウトの表現力とも相まって、非常にややこしい処理となっていますが、計算機に都合が良いように計算途中のデータを自動で大規模に並べ替えるというのは汎用計算のコンパイラではなかなかできない最適化であり、深層学習コンパイラの真骨頂ともいえる部分じゃないかと思います。今回のブログ記事はその入り口となるレイアウト表現だけを扱いましたが、メモリレイアウトの計算・最適化という問題に興味を持っていただけたら嬉しいです。




