Blog
本記事は、2021年インターンシップで勤務した 篠原航平 さんによる寄稿です。
English version is available here.
はじめに
2021年夏季インターンシップに参加した京都大学の篠原航平です。本記事では「電荷移動を考慮したNeural Network Potential」というテーマで取り組んだ内容について説明します。
実装はこちらに公開されています。
また、テーマ内容のスライドはこちらにアップロードされています。
背景
材料開発・研究の分野では、原子スケールでの物質シミュレーションを行うために密度汎関数法(Density Functional Theory, DFT)に基づく計算が広く行われています。DFT計算はSchrödinger方程式を解くことで物質の電子状態やエネルギーを計算するもので、多くの物質系で高い精度で予測できることが知られています。一方、DFT計算は計算時間の面で高コストであり、大規模または長時間のシミュレーションを行うには課題があります。
この課題を解決するために、近年Neural Network Potential (NNP) [1] と呼ばれる手法が活発に研究されています。NNPとは、大量のDFT計算をデータセットとしてNeural Network (NN)にその出力を予測させるもので、DFT計算に近い計算精度と高速な予測を両立できる可能性を秘めた手法として注目されています。2021年PFNとENEOSが共同出資により設立したPreferred Computational Chemistryが提供を開始した汎用原子レベルシミュレータMatlantisにおいて、NNPはコア技術にもなっています。
しかし、従来のNNPでは予測が難しい物質系も存在します。通常NNPでは、各原子について近傍原子からの寄与だけを考慮することで、計算時間を短縮しています。しかし、この方式では長距離相互作用を無視できないような物質系に課題が残ります。長距離相互作用の考慮が重要な系としては、物質表面上での触媒やイオン性結晶などが挙げられます。この長距離相互作用は物理的には原子間での電荷移動(charge transfer) [6]に由来しています。そのため、この数年で電荷移動を考慮したNNPの研究も行われるようになりました [2-5]。
これらの電荷移動を考慮したNNPの中でも代表的なものとして、Fourth-Generation Behler-Parrinello Neural Network Potential (4G-HDNNP, 以下では4G-BPNNと記載) [4]があります。この論文ではQeqと呼ばれる電荷移動に関する古典的な手法(後述)とNNを組み合わせることで予測精度が向上すると報告しています。一方で4G-BPNNはMultilayer perceptron (MLP)をベースとしたモデルになっており、近年NNPにおいて主流になりつつあるGraph Neural Network (GNN)においてそれらの提案された手法がどの程度効果をもつかは明らかでありませんでした。そこで今回のインターンシップでは4G-BPNNで提案された手法をGNNベースで実装し、その効果の検証を行いました。
手法
次に実装のベースとしたGNNの紹介をし、長距離相互作用を取り込むための静電相互作用項の計算、およびCharge equilibrationと呼ばれる電荷の予測手法を説明します。詳細についてはスライド及び参考文献を参照ください。
GNN Based NNP
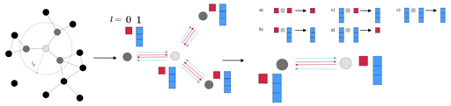
図1: NequIPの概要([7]より引用)。
NNPのベースラインモデルとしては Neural Equivariant Interatomic Potentials (NequIP) [7] (pytorch実装は [8])を用いました(図1)。NequIPはGNNベースのモデルで、畳み込み層が各原子の記述子を近傍原子を元に更新します。また、NNPは入力する構造に並進・回転操作を加えたときに出力が不変であることが要請されますが、NequIPはモデル自体がその不変性を保証しています。このようなモデルはSE(3)-equivariant network [9, 10]と呼ばれています。
静電相互作用項
長距離相互作用のエネルギーを計算するために、GNNで得られる各原子の記述子から電荷を予測し、その電荷から静電相互作用(下式)を計算しました [4]。
$$
E_{\mathrm{ele}}(\{Q_{i}\}) = \frac{1}{2} \frac{1}{4\pi \epsilon_{0}} \int \int \frac{\rho(\mathbf{r}) \rho(\mathbf{r}’)}{|\mathbf{r} – \mathbf{r}’|} d\mathbf{r} d\mathbf{r}’
$$
電荷の予測に関しては、各原子の記述子から直接予測する方法と、次節で紹介するQeqを用いて予測する方法を検討しました。
また、入力する構造が結晶のように周期系の場合にはEwald summation [11-13]のような特別な手法が静電相互作用項の計算に必要となります。現状Ewald summationのpytorch実装は見つけられなかったため、今回新たに実装しました。
Charge Equilibration
4G-BPNN [4]やその前身であるCENT [2]では電荷の予測にCharge Equilibration (Qeq) [14, 15]と呼ばれる古典的な手法を用いています。Qeqは電荷由来のエネルギーへの寄与を次式
\[
E_{\mathrm{Qeq}}(\{ Q_{j} \}) = E_{\mathrm{ele}}(\{ Q_{j} \}) + \sum_{i} \left( \chi_{i} Q_{i} + \frac{1}{2} J_{i} Q_{i}^{2} \right)
\]
のようにモデル化し、\(E_{\mathrm{Qeq}}\)が最小になるように電荷\(Q_{i}\)を求めます。NNにQeqを組み合わせる場合には、\(\chi_{i}\)や\(J_{i}\)のような\(E_{\mathrm{Qeq}}\)を計算するために必要なパラメターをNNによって予測します。
実装の観点では、Qeqはある線型方程式系の解を求めることに帰着されます。pytorch実装ではこれはtorch.linalg.solveを用いて実現でき、自動微分を活用することで線型方程式系の解の微分といった煩雑な実装を回避することができます。
結果と考察
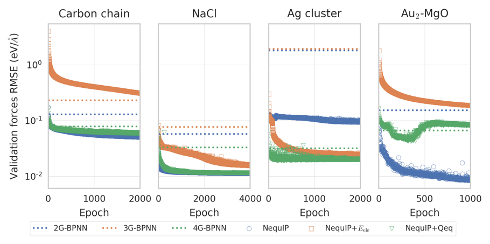
図2: 各原子にはたらく力の予測精度の比較
4G-BPNN論文で使われていたデータセット (スライドp9参照)に対してNNPを学習し、各原子にはたらく力を予測させたときの精度をプロットしたものが図2になります。縦軸は予測精度を表しており、下にいくほど精度が高いです。緑の点線は4G-BPNN(MLP+Qeq)、青はベースラインのGNN、オレンジはGNNで電荷を直接予測して静電相互作用項の補正をしたもの、緑はGNNとQeqを組み合わせて電荷予測と静電相互作用項を補正をしたものです。
電荷の予測方法に関して、各原子の記述子から直接電荷を予測する(オレンジ)よりもQeqを経由して電荷を予測(緑)する方が予測精度が高くなっています。これは4G-BPNN論文でも報告されている傾向で、GNNでもローカルな情報だけでは電荷を予測するタスクを解くのは難しく、Qeqのような構造全体を考慮する手法が効果的であると考えられます。
一方、Ag cluster以外のデータセットでは、そもそもベースラインの電荷を考慮しないモデルが最も精度が高いという結果を得ました。また、ベースラインの精度はどれも4G-BPNNよりも良くなっています。MLPではあるカットオフ半径内の原子しか考慮できず、それを超えた部分を考慮するために電荷予測と静電相互作用補正が効いているものと考えられます。一方で、GNNでは畳み込み層を重ねることで実質的なカットオフ半径を広げることができ、今回用いたデータセットではGNN側が静電相互作用項の効果を吸収してしまったものと考えられます。Ag clusterのデータセットに関しては考察が難しいですが、静電相互作用項を入れることでモデルの表現力が上がり予測精度が向上したのではないかと考えています。
まとめ・謝辞
本インターンシップでは、原子スケールでの物質シミュレーションにおいて電荷移動の効果を取り込むための手法を実装し、その効果をGNNベースのNNPにおいて検証しました。そして、MLPベースのNNPにおいて有効だった手法がそのままGNNでも使えるわけでないが、Qeqという古典的な手法を用いること自体は電荷予測の精度向上に寄与するという結果を得ました。
約1ヶ月半というテーマの立ち上げから実験を行うまでには短い期間でしたが、メンターの中郷さん、副メンターの林さん、その他材料探索チームの方々の手厚いサポートのおかげで充実したインターンシップとなりました。最後になりますが、この場を借りて御礼申し上げます。
参考文献
[1] Jörg Behler and Michele Parrinello, Generalized Neural-Network Representation of High-Dimensional Potential-Energy Surfaces, [Phys. Rev. Lett. 98, 146401 (2007)](https://journals.aps.org/prl/abstract/10.1103/PhysRevLett.98.146401).
[2] S. Alireza Ghasemi, Albert Hofstetter, Santanu Saha, and Stefan Goedecker, Interatomic potentials for ionic systems with density functional accuracy based on charge densities obtained by a neural network, [Phys. Rev. B 92, 045131 (2015)](https://journals.aps.org/prb/abstract/10.1103/PhysRevB.92.045131).
[3] Zhi Deng, Chi Chen, Xiang-Guo Li and Shyue Ping Ong, An electrostatic spectral neighbor analysis potential for lithium nitride, [Npj Comput. Mater. 5, 75 (2019)](https://www.nature.com/articles/s41524-019-0212-1).
[4] Tsz Wai Ko, Jonas A. Finkler, Stefan Goedecker, and Jörg Behler, A fourth-generation high-dimensional neural network potential with accurate electrostatics including non-local charge transfer, [Nat. Commun. 12, 398 (2021)](https://www.nature.com/articles/s41467-020-20427-2).
[5] Oliver T. Unke, Stefan Chmiela, Michael Gastegger, Kristof T. Schütt, Huziel E. Sauceda, and Klaus-Robert Müller, SpookyNet: Learning Force Fields with Electronic Degrees of Freedom and Nonlocal Effects, [arXiv:2105.00304](https://arxiv.org/abs/2105.00304).
[6] Anthony Stone, [The Theory of Intermolecular Forces](https://global.oup.com/academic/product/the-theory-of-intermolecular-forces-9780199672394?cc=jp&lang=en&) (Oxford University Press, Oxford, 2013).
[7] Simon Batzner, Albert Musaelian, Lixin Sun, Mario Geiger, Jonathan P. Mailoa, Mordechai Kornbluth, Nicola Molinari, Tess E. Smidt, and Boris Kozinsky, SE(3)-Equivariant Graph Neural Networks for Data-Efficient and Accurate Interatomic Potentials, [arxiv:2101.03164](https://arxiv.org/abs/2101.03164).
[8] https://github.com/mir-group/nequip
[9] Nathaniel Thomas, Tess Smidt, Steven Kearnes, Lusann Yang, Li Li, Kai Kohlhoff, and Patrick Riley, Tensor field networks: Rotation- and translation-equivariant neural networks for 3D point clouds, [arXiv:1802.08219](https://arxiv.org/abs/1802.08219).
[10] https://e3nn.org/
[11] http://micro.stanford.edu/mediawiki/images/4/46/Ewald_notes.pdf
[12] Todd R.Gingrich and Mark Wilson, On the Ewald summation of Gaussian charges for the simulation of metallic surfaces, [Chem. Phys. Lett. 500, 1-3, 10 (2010)](https://www.sciencedirect.com/science/article/abs/pii/S0009261410013606?via%3Dihub).
[13] Péter T Kiss, Marcello Sega, and András Baranyai, Efficient Handling of Gaussian Charge Distributions: An Application to Polarizable Molecular Models, [J. Chem. Theory Comput. 10, 12 (2014)](https://pubs.acs.org/doi/10.1021/ct5009069).
[14] Anthony K. Rappe and William A. Goddard III, Charge equilibration for molecular dynamics simulations, [J. Phys. Chem. 95, 8, 3358-3363 (1991)](https://pubs.acs.org/doi/pdf/10.1021/j100161a070).
[15] Christopher E. Wilmer, Ki Chul Kim, and Randall Q. Snurr, An Extended Charge Equilibration Method, [J. Phys. Chem. Lett. 3, 17, 2506-2511 (2012)](https://pubs.acs.org/doi/10.1021/jz3008485).