Blog
背景
Preferred Networks(以下PFN)とグループ会社のPreferred Elements(以下PFE)では10月から高性能かつ軽量なLLMの開発を行っています。その中で、予備実験・検証として10億 (1B) パラメータ規模のLLM (PLaMo 2 1B) の学習を行いました。今回の記事では、このモデルの開発について紹介します。
この開発は経済産業省及び国立研究開発法人新エネルギー・産業技術総合開発機構(NEDO)が提供する、国内の生成AIの開発力を強化するためのプロジェクト「GENIAC(Generative AI Accelerator Challenge)」の計算資源の提供支援を受けて実施しました。
GENIAC 第2期におけるPFNとPFEの目標
今回PFNとPFEではモデルサイズを抑えたまま高い性能を実現するために高品質なデータを作成し、そのうえで状態空間モデル(SSM)を採用した小規模なモデルで高い精度を達成することを目標に活動しています。
特に、幅広い知識を測定するJMMLUやコーディングタスクであるJHumanEvalにおいて高い精度を達成することを目的の一つとしています。ここでは、現時点で得られた1Bモデルの性能検証を行った予備実験の結果と学習においてどのような工夫をしたのかについて紹介します。
評価結果
まずは予備実験として開発したPLaMo 2 1Bの精度についてまとめて示し、そのあと結果の考察を述べます。
今回は英語と日本語の両方で幅広い知識を測定するためにMMLUと主にその日本語訳であるJMMLU を使った評価と、コーディング能力を測定するためにHumanEval+、JHumanEvalで評価しました。また、比較対象には2B以下のモデルで、事前学習のデータに日本語が含まれていると考えられる事前学習済みモデルを選びました。ただし、gemma-2-2bに関しては日本語で継続学習されたモデルはinstruction済みモデルのみ公開されているため、gemma-2-2bの事前学習モデル(ただしこれは日本語はほとんど含まれていないと思われます)と日本語の継続学習がされたgemma-2-2b-jpn-itを比較対象として加えました。このため、gemma-2-2b-jpn-itだけは他のモデルとの傾向が違うと考えられます。また、データセットなどの改善がうまくいっているかの確認のために、以前開発した同レベルのパラメータ数であるPLaMo-Lite (事前学習モデル)も比較対象として評価しました。
まず、JMMLUに関しては公開されているtestデータの各項目の5つのサンプルをランダムに選びfew shotの入力として利用して測定しました。評価にはLanguage Model Evaluation Harness ( https://github.com/EleutherAI/lm-evaluation-harness ) のMMLUのコードを改良して実施しました。
また、JMMLUの評価のpromptとしてLanguage Model Evaluation HarnessのMMLUで実装されているdefault(選択肢をLLMに入力し、A,B,C,Dの選択肢を答えさせる方法)と、continuation(選択肢を見せずに選択肢の文章の尤度が一番高いものを選ぶ方法)の2種類を測定しました。
結果は以下の通りです。
表1: JMMLUの評価結果
| default(5 shot, acc)* | continuation(5 shot, acc_norm)** | |
| sbintuitions/sarashina2.1-1b | 0.258 | 0.362 |
| llm-jp/llm-jp-3-1.8b | 0.264 | 0.334 |
| meta-llama/Llama-3.2-1B | 0.281 | 0.294 |
| google/gemma-2-2b | 0.259 | 0.264 |
| google/gemma-2-2b-jpn-it | 0.382 | 0.298 |
| Qwen/Qwen2-1.5B | 0.469 | 0.303 |
| PLaMo Lite (事前学習モデル) | 0.333 | 0.338 |
| PLaMo 2 1B | 0.334 | 0.352 |
*: LLMに質問とA,B,C,Dの4つの選択肢が入力されて、LLMは正解となる選択肢をアルファベットで回答させるやり方。promptの詳細はAppendix参照
**: LLMに質問と選択肢のテキストを与えて、最も選択肢のテキストの尤度が高くなるものを正解として選ぶやり方。promptの詳細はAppendix参照
次にMMLUの評価結果です。MMLUはLanguage Model Evaluation Harness ( https://github.com/EleutherAI/lm-evaluation-harness ) を利用しました。こちらもJMMLUと同様にdefaultとcontinuationの2種類を測定しました。結果は以下の通りです。
表2: MMLUの評価結果
| モデル | default(5 shot, acc)* | continuation(5 shot, acc_norm)** |
| sbintuitions/sarashina2.1-1b | 0.253 | 0.368 |
| llm-jp/llm-jp-3-1.8b | 0.249 | 0.343 |
| meta-llama/Llama-3.2-1B | 0.312 | 0.375 |
| google/gemma-2-2b | 0.328 | 0.300 |
| google/gemma-2-2b-jpn-it | 0.498 | 0.410 |
| Qwen/Qwen2-1.5B | 0.561 | 0.394 |
| PLaMo Lite (事前学習モデル) | 0.265 | 0.360 |
| PLaMo 2 1B | 0.290 | 0.349 |
*: JMMLUと同じようにLLMに質問とA,B,C,Dの4つの選択肢が入力されて、LLMは正解となる選択肢をアルファベットで回答させるやり方。promptの詳細はAppendix参照
**: JMMLUと同じようにLLMに質問と選択肢のテキストを与えて、最も選択肢のテキストの尤度が高くなるものを正解として選ぶやり方。promptの詳細はAppendix参照
次にコーディングタスクの結果は以下の通りです。
表3: コーディングタスクの結果
| モデル | JHumanEval(0-shot, pass@1)* | HumanEval+(0-shot, pass@1)** |
| sbintuitions/sarashina2.1-1b | 0.073 | 0.073 |
| llm-jp/llm-jp-3-1.8b | 0.000 | 0.006 |
| meta-llama/Llama-3.2-1B | 0.116 | 0.134 |
| google/gemma-2-2b | 0.171 | 0.159 |
| google/gemma-2-2b-jpn-it | 0.317 | 0.335 |
| Qwen/Qwen2-1.5B | 0.085 | 0.165 |
| PLaMo Lite (事前学習モデル) | 0.043 | 0.055 |
| PLaMo 2 1B | 0.189 | 0.232 |
*: 評価の詳細ははAppendix参照
**: 評価の詳細ははAppendix参照
これに加えて、日本語のLLMの評価でよく使われるJCommonSenseQAとJSQuADの精度を以下に示します。
表4: JCommonSenseQAとJSQuADの結果
| モデル | JCommonSenseQA(3 shot, acc_norm)* | JSQuAD(2 shot, F1)** |
| sbintuitions/sarashina2.1-1b | 0.326 | 89.343 |
| llm-jp/llm-jp-3-1.8b | 0.274 | 75.257 |
| meta-llama/Llama-3.2-1B | 0.253 | 59.391 |
| google/gemma-2-2b | 0.230 | 2.129 |
| google/gemma-2-2b-jpn-it | 0.603 | 77.972 |
| Qwen/Qwen2-1.5B | 0.481 | 72.523 |
| PLaMo Lite (事前学習モデル) | 0.335 | 81.774 |
| PLaMo 2 1B | 0.551 | 77.663 |
*: Stability AIのlm-evaluation-harnessのjcommonsenseqa-1.1-0.2.1 と同じデータ、promptで測定
**: Stability AIのlm-evaluation-harnessのjsquad-1.1-0.2 と同じデータ、promptで測定。ただし、DYNAMIC_MAX_LENGTH=Falseで実行。
評価結果の考察
JMMLU/MMLUとJHumanEval/HumanEval+に関して
まずJMMLUとMMLUに関してです。MMLUは小さいモデルや少ない学習token数のモデルではdefaultの評価方法、つまり、選択肢をLLMに入力し、A,B,C,Dの選択肢を答えさせる方法ではほぼランダムに選んだ場合(チャンスレベル)の0.25前後の値になっていることが多いことが知られています。一方、continuationの評価方法、つまり、選択肢を見せずに選択肢の文章の尤度が一番高いものを選ぶ方法ではdefaultの評価方法ではチャンスレベル付近の精度だったモデルでも精度がチャンスレベルよりも高い精度になります。JMMLUに関してもMMLUと似たような傾向があることが先ほどの結果からも見て取ることができます。これと似たような考察はdatacomp-lm に書かれていますので詳しく知りたい方はこちらをご覧ください。
実際、JMMLUとMMLUのどちらもdefaultの評価ではいくつかのモデルでチャンスレベル付近の精度になっていることがわかります。一方continuationの評価ではほぼどのモデルもチャンスレベルより高い精度になっています。google/gemma-2-2bのみJMMLUのcontinuationの評価でほぼチャンスレベルの精度になっていますが、これはもともと日本語で学習されていないためであると考えられます。
ただ、結果についてよく見比べてみると海外勢の1Bモデル(meta-llama/Llama-3.2-1B, google/gemma-2-2b, Qwen/Qwen2-1.5Bなど)に関しては精度が低いながらもdefaultの評価でもチャンスレベルよりも高い精度になっています。
これに加えて、コーディングタスクのJHumanEvalやHumanEval+に関してもコーディングに特化しない汎用的な事前学習モデルに関しては、ただGitHub由来のコードデータを入れて学習しただけではなかなか精度が上がってこないということがこれまでの検証で見えてきました。一方コーディングタスクに関しても海外勢のモデルに関してはどれも日本のLLMのモデルよりも高い精度になっています。
このことから1BでもJMMLUとMMLUに関してはdefaultの評価でチャンスレベルよりも十分高い精度に達成することと、JHumanEvalとHumanEval+において、日本語と英語などのコード以外のデータを十分含めて学習した事前学習モデルで10%以上のスコアを達成するということがGENIAC 第2期の目標で重要であると我々は考えました。
このため、PLaMo 2 1Bのデータセットの準備の際、JMMLUやMMLUのdefaultの評価でも精度があがりそうかや、コーディングタスクにおいて精度が上がってくるかをある程度の規模(8Bモデルで100B token学習するなど)の学習を行って定期的に確認をしながらデータの準備を行いました。結果としてPLaMo-Lite (事前学習モデル)とPLaMo 2 1Bの比較においては、JMMLUに関してはPLaMo-Lite (事前学習モデル)の時点でチャンスレベルより高い精度を達成できていましたが、MMLUのdefaultの評価においてPLaMo-Lite (事前学習モデル)はチャンスレベルとほぼ変わらない0.265という精度でした。一方、PLaMo 2 1Bは0.290とチャンスレベルより上がってきている傾向を確認できました。また、JHumanEvalとHumanEval+に関してもPLaMo-Lite (事前学習モデル)は0.043と0.055とほぼ解けていない状態だったのに対してPLaMo 2 1Bは0.189と0.232という精度まで到達するという期待通りの結果を得ることができました。
日本語固有の問題に対する深堀り
上述の通り、PLaMo 2 1BはMMLUやHumanEvalといった言語への依存があまりないベンチマークにおいて、海外製モデルに近い能力を獲得できました。
しかし、日本においてLLMを活用することを考えると、日本語固有の知識も重要となります。数学やコーディングといった能力は言語によらずほぼ同じものが要求されると考えられますが、例えば地理や法律などは国ごとに重点を置くべき知識に差がありそうです。
こういった日本語固有の知識について、ベンチマーク結果からPLaMo 2 1Bの能力を見ていきます。
JMMLU 日本問題
JMMLUには日本問題という、MMLUからの翻訳ではない問題があります。熟語、公民、日本地理、日本史の4タスクからなるこれらの問題は、英語ではあまり問われることのない日本語固有の知識・問題が集まっています。
これらJMMLU 日本語問題の性能を通して、各モデルの日本語固有知識について見ていきます。default (4択による評価) だと選択肢問題に答えられずランダムと変わらない結果になってしまうモデルも多いので、continuationの評価方法をここでは採用します。その他の設定はJMMLU全体の結果と同じです。
表5. JMMLU (continuation) から日本問題を抜粋
| モデル | 熟語 | 公民 | 日本地理 | 日本史 |
| sbintuitions/sarashina2.1-1b | 0.84 | 0.78 | 0.75 | 0.61 |
| llm-jp/llm-jp-3-1.8b | 0.77 | 0.68 | 0.63 | 0.55 |
| meta-llama/Llama-3.2-1B | 0.50 | 0.48 | 0.34 | 0.31 |
| google/gemma-2-2b | 0.30 | 0.33 | 0.25 | 0.25 |
| google/gemma-2-2b-jpn-it | 0.48 | 0.41 | 0.29 | 0.30 |
| Qwen/Qwen2-1.5B | 0.51 | 0.46 | 0.35 | 0.29 |
| PLaMo-Lite (事前学習モデル) | 0.78 | 0.70 | 0.73 | 0.55 |
| PLaMo 2 1B | 0.79 | 0.75 | 0.73 | 0.51 |
日本問題だけを取り出してみると、日本で学習されたモデルと海外で学習されたモデルで大きく傾向が違うことがわかります。日本語で学習されたsbintuitions/sarashina2.1-1b、llm-jp/llm-jp-3-1.8bおよびPLaMoは、どのタスクでも海外製LLMより高い性能を示しています。
google/gemma2-2b-jpn-itは日本問題については大きな性能の改善が見られていません。このモデルはおそらくgemma-2-2bを比較的少量の日本語指示学習データで指示学習したものと考えられますが、日本語固有の知識は日本語の学習量が極めて重要であることがわかります。
PLaMo 2 1Bは、PLaMo-Liteを含む日本で学習されたモデルと同等程度の性能をJMMLU 日本問題で発揮しています。1Bとモデルサイズが小さいことから新しい能力を得ると元々学習できていた能力を失うというようなトレードオフがある可能性も考えられます。しかし、この結果をみるとPLaMo 2 1Bはコーディング能力など言語に依存しない能力を追加した代わりに日本語固有の知識を失ったのではなく、双方を両立できていると言えると思います。
JSQuAD
PLaMo 2 1BはJSQuADにおいてPLaMo-Liteより性能が落ちています。この原因について簡単にですが調査しました。
現在のところ、原因の1つとして、数学能力などの強化のためChain of Thought (CoT) 能力を重視したことが影響しているのではないかと考えています。PLaMo LiteとPLaMo 2 1BのJSQuADの回答の文字数をみると
- PLaMo Lite(事前学習済みモデル): 中央値 5文字、最大76文字
- PLaMo 2 1B: 中央値 6文字、最大753文字
であり、PLaMo 2 1Bはまれに非常に長い出力をしていることがわかります。これがPLaMo-Liteと比較してF1スコアを下げる要因となっていそうです。
JMMLU 日本問題のスコアをみると、日本語固有の知識という点ではPLaMo-LiteとPLaMo 2 1Bに大差はないと予想できます。そのため、この問題は事後学習のアラインメントによって解決できるのではないかと考えています。
学習の詳細
ここからは、今回の学習で取り組んだことについて2点ピックアップして紹介します。1つはLLMのモデルアーキテクチャについて、もう1つは学習に用いたデータセットについてです。
モデルアーキテクチャの変更
LLMのモデルアーキテクチャは、学習の安定性、学習・推論における効率、モデルの性能など様々な能力に影響する重要な要素です。論文などにおいて様々なアーキテクチャの変更が提案され、そのなかでもRMSNormやGrouped Query Attention (GQA) などは広く採用されるものになりました。
PFEでもLLMアーキテクチャについての試行錯誤を繰り返してきました。継続事前学習を行わずに0からの事前学習を行うからこそできることとして取り組む価値があると考えてきたためです。例えば、2024年夏のGENIAC 第1期では、QK Normalizationの採用などを行っています。
これまでのPLaMoは一貫してTransformerをベースとしたアーキテクチャを採用してきました。これは、2024年現在でもオープンなLLMのほとんどはTransformerをベースとしており、学習速度、達成できる性能などの面で最も成功確率が高いアーキテクチャであるためです。
一方で、Transformerは系列長が長くなる際の推論に問題があることが知られています。学習時の系列長を超えた推論をするには工夫が必要であること、そもそも系列長が長くなると、メモリ消費が大きくなり推論ができないあるいは遅くなること、の2点が特に大きな問題となっています。
今回この問題に対処するために、我々はSambaをベースとしたアーキテクチャにすることで、主に後者の問題に対処することとしました。Sambaは状態空間モデル(SSM)であるMambaとsliding window attentionを組み合わせたモデルアーキテクチャで、以下の特徴があります。
- 学習時の系列長を超えても、推論・生成が破綻せずに行える
- 系列長が伸びてもメモリ消費や計算量が増加しない
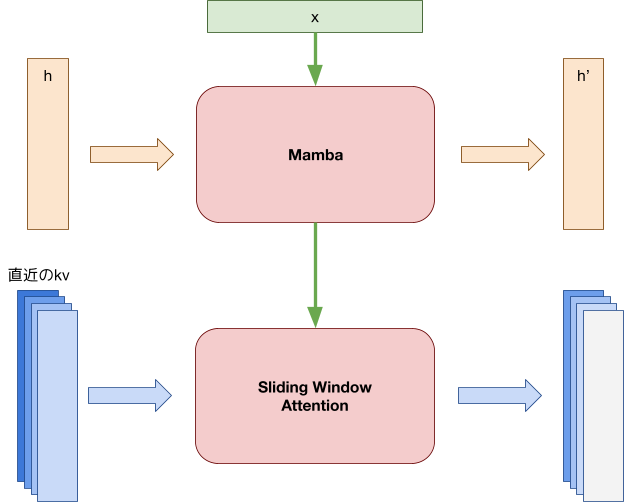
図1: Sambaのアーキテクチャ。MambaaとSliding Window Attentionを重ねる。
Mambaを使ったモデルは、上記の利点がある一方で、モデルを大きくするとTransformerと比べて学習が不安定という問題があります。
この問題に対しては、JambaやGemma2を参考にRMSNormレイヤを追加することで対応しました。
事前の社内実験では、学習安定化の工夫なしだと以下のグラフのように大きなloss spikeが発生していました。しかし、RMSNormを追加した後は大きなloss spikeはなく学習することができています。
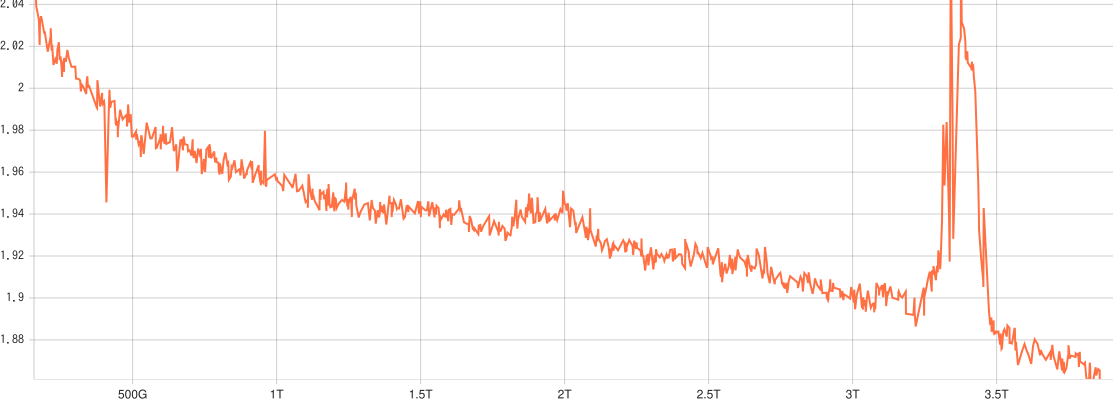
図2: 9月に行った事前実験のlearning curve。学習後半で大きなloss spikeが発生している。
データセット
GENIAC 第2期において、PFEでは学習データセットの改善を注力するポイントとしています。今回のモデルの学習でもさまざまな工夫を行なって準備したデータセットを使用し、性能向上を目指しました。
このブログでは、日本語データセットについての取り組みを3つ紹介します。
Webデータのフィルタリング
fineweb-eduやdatacomp-lmなど最近の英語データセットではwebデータを何らかの指標のもとフィルタリングすることでデータセットを改善するアプローチが採用されています。日本語データセットでもLlama-3.1-swallowがこのようなフィルタリングを採用しています。
これらの最近の研究に基づき、我々も日本語データのフィルタリングを新たに行うことにしました。
今回の学習では、以下の2種類のフィルタリングを併用しています。
- fineweb-eduのような教育的価値におけるフィルタリング
- webデータに多数含まれるカテゴリのdown sampling
2つのフィルタリングを併用することには、データセットの前処理などが煩雑になるという問題があります。しかし、教育的価値のみに頼った場合のリスクを無視できないと判断しました。例えば、webページの広告は教育的価値を基準にすると削除されがちなテキストですが、広告の分類などのタスクを考えた時、事前学習データセットから一切排除してしまうのは適切ではない可能性があります。
2.のdown samplingでも、広告のようなwebデータに多く含まれる文章はある程度の個数削除されますが、一定の割合ではフィルタリング後のデータセットにも残ります。そのため、教育的価値のみを使う方法と比べ想定外の性能劣化を起こすリスクが少ないと考えています。
どちらについても、まず指示学習を行った後のPLaMo-100B (以下PLaMo-100B) を用いてある程度の規模のデータにアノテーションを行い、アノテーション結果をもとにより軽量なモデルを学習してデータセット全体のフィルタリングに用いました。
既存データの言い換え
データセットのフィルタリングだけでなく、生成自体にもLLMを活用しました。
LLMによるデータセット合成としては、cosmopediaのようなprompt engineeringによって様々なデータを生成するという手法が広く知られています。
この方法の有効性はphiシリーズのモデルで実証されていますが、データ生成のためのpromptの良し悪しが生成されたデータの有効性を大きく左右することが報告されています。また、データの生成にモデルの知識を使うため、生成に使うLLMが苦手な分野のテキストを生成するのは困難です。
今回、我々は主にPLaMo-100Bによる既存のデータの言い換えを通してデータ生成することとしました。言い換え元のテキストを知識源として使うので、LLM自体の知識にはあまり依存せずデータを生成できます。
また、言い換え元のデータとして英語データを言い換えたあと、そこから日本語データにする、すなわち翻訳を行う場合、prompt engieeningのコストを大幅に減らすことができます。英語を日本語に翻訳するprompt自体は、多少の工夫は必要であっても比較的簡単に作ることができます。
英語データとして存在する知識量は日本語に比べて遥かに多く、これらを使い効率的に日本語データを増やすことができました。
翻訳によるデータ生成は日本語固有の知識などの欠如などを起こす可能性はあります。例えば英語データの翻訳だけで日本の法律に関する十分な知識が得られるとは考えにくいです。こういった問題に対しては、
- 数学など言語固有の知識が少ない分野を重点的に扱う
- 翻訳データだけに頼るのではなく、もともとの日本語データも用いる
の2つの方法で対処できていると考えています。
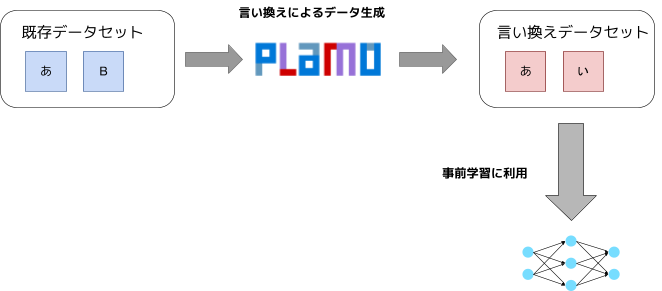
図3: 言い換えデータセットの作成と利用ワークフロー
LLMでアノテーションしたデータセットに対するself-tuning
最後に、self-tuningによるデータ生成について紹介します。最近の研究では、事前学習の時点から指示学習向けのようなデータを入れることがLLMの性能向上に寄与すると報告されています。また、LLMを使って指示学習データセット向けのデータを作る方法はいくつか (例: self-instruct)提案されており、現在比較的一般的なものとなっています。
しかし、LLMで生成した指示学習向けデータを事前学習で使うことは生成速度の点で困難です。事前学習のデータセットとして用いるには十分な量が必要ですが、高性能なLLMを使ってデータ生成するとそれだけの量を確保するのが困難になります。既存の研究ではこの問題に対し、データ生成用にfine tuningしたモデルを使うことで対処していますが、fine tuningのために多様なデータセットが必要であることなどの課題があり、日本語データにすぐに応用できる状況ではありません。
一方、self-tuningはルールベースに指示学習データを作る手法であり、生成速度などの問題を解決できる可能性を持っています。一方で、データセットについているメタデータ (タイトルなど) を使う手法であるため、元にするデータセットに制限があります。つまり、生成速度には問題はありませんが、元データセットのサイズが原因で大量にデータ生成することが困難となります。
今回我々は、PLaMo-100Bを用いて、テキストの要約などいくつかの情報をアノテーションし、この情報を用いてself-tuningで指示・応答のペアを作るという方針をとりました。
これにより、大量 (utf8のテキストで600GB前後) の指示・応答データを現実的な計算コストで生成しました。この時、英語データセットの指示・応答ペアなどを参考にself-tuningにはなかったタスクについての追加も行い、データの多様性をさらに増やしました。
最後に
今回は、GENIAC 第2期における事前学習の取り組みについて紹介しました。現在はこの結果をもとによりモデルサイズなどの規模を大きくした事前学習の実験に移ると同時に、PLaMo 2 1Bの事後学習を進めています。
今回学習したPLaMo 2 1Bに関しては何等かの形でモデルの重みを公開することを検討しています。
現在こちらのPLaMo 2 1BモデルをHugging Faceで公開していますので、興味がある方はダウンロードしてご利用いただければと思います。
https://huggingface.co/pfnet/plamo-2-1b
仲間募集中
PFN/PFEでは今後もLLMの開発を継続して行っていきます。開発は今回紹介した以外にも多岐に渡ります。我々はこれらの課題に情熱をもって挑戦していく仲間を募集しています。
これらの仕事に興味がある方はぜひご応募よろしくお願いします。
Appendix
JMMLUのdefaultにおけるprompt
JMMLUのdefaultで利用したpromptは以下の通りです。
選択問題 問題: 48以上88以下=?以上11以下が成り立つ数を求めよ。 A. 6 B. 11 C. 8 D. 5 回答: A … 問題: ペレスさんは5日間で合計40マイルを運転した。毎日同じ距離を走った。ペレスさんは毎日何マイルを運転したか。 A. 5 B. 7 C. 8 D. 9 回答:
JMMLUのcontinuationにおけるprompt
JMMLUのcontinuationで利用したpromptは以下の通りです。
選択問題 問題: 48以上88以下=?以上11以下が成り立つ数を求めよ。 回答: 6 … 問題: ペレスさんは5日間で合計40マイルを運転した。毎日同じ距離を走った。ペレスさんは毎日何マイルを運転したか。 回答:
MMLUのdefaultにおけるprompt
MMLUのdefaultで利用したpromptは以下の通りです。
The following are multiple choice questions (with answers) about elementary mathematics. The population of the city where Michelle was born is 145,826. What is the value of the 5 in the number 145,826? A. 5 thousands B. 5 hundreds C. 5 tens D. 5 ones Answer: A … What is the value of p in 24 = 2p? A. p = 4 B. p = 8 C. p = 12 D. p = 24 Answer:
MMLUのcontinuationにおけるprompt
MMLUのcontinuationで利用したpromptは以下の通りです。
The following are multiple choice questions (with answers) about elementary mathematics. The population of the city where Michelle was born is 145,826. What is the value of the 5 in the number 145,826? Answer: 5 thousands … What is the value of p in 24 = 2p? Answer:
JHumanEvalの評価方法
promptは https://huggingface.co/datasets/kogi-jwu/jhumaneval のpromptをそのまま利用しました。
例を以下に示します。
from typing import List
def has_close_elements(numbers: List[float], threshold: float) -> bool:
"""リストnumbersの中に、与えられたthresholdより近い2つの数値が存在するか判定する
>>> has_close_elements([1.0, 2.0, 3.0], 0.5)
False
>>> has_close_elements([1.0, 2.8, 3.0, 4.0, 5.0, 2.0], 0.3)
True
"""
また、LLMのコードの生成は以下のものでも止まるようにしました
[ "\nclass", "\ndef", "\n#", "\n@", "\nprint", "\nif", "\n```", "<file_sep>", "\nimport", "\nfrom"]
HumanEval+
promptはhttps://huggingface.co/datasets/evalplus/humanevalplus のpromptをそのまま利用しました。
例を以下に示します。
from typing import List
def has_close_elements(numbers: List[float], threshold: float) -> bool:
""" Check if in given list of numbers, are any two numbers closer to each other than
given threshold.
>>> has_close_elements([1.0, 2.0, 3.0], 0.5)
False
>>> has_close_elements([1.0, 2.8, 3.0, 4.0, 5.0, 2.0], 0.3)
True
"""
また、LLMのコードの生成は以下のものでも止まるようにしました。
[ "\nclass", "\ndef", "\n#", "\n@", "\nprint", "\nif", "\n```", "<file_sep>", "\nimport", "\nfrom"]